Волновая оптика Свет это электромагнитная волна Совокупность

Волновая оптика Свет – это электромагнитная волна. Совокупность явлений, в основе которых лежит волновая природа света, изучается в разделе физики, который называется волновая оптика. Оптический диапазон длин волн обычно подразделяют на: - ультрафиолетовое излучение - видимое излучение (свет) - инфракрасное излучение - =0, 01 0, 40 мкм; =0, 40 0, 76 мкм; =0, 76 мкм 100 мкм; В электромагнитной волне колеблются векторы и. Многие действия света вызываются колебаниями вектора. Поэтому обычно говорят о световом векторе, подразумевая под ним вектор напряженности электрического поля. Соответственно, уравнение световой волны будет выглядеть так: 1

В веществе длина световой волны отличается от ее длины в вакууме. Фазовая скорость световой волны в веществе , длина волны связана с частотой колебаний выражением. В итоге . Интерференция световых волн Принцип Гюйгенса – каждая точка, до которой доходит волновое движение, служит центром вторичных волн, которые в однородной и изотропной среде будут сферическими. В области перекрытия двух волн наблюдается сложение (суперпозиция) волн и после выхода из этой области каждая волна распространяется так, как если бы никакого перекрытия не было. Результаты таких сложений определяются тем, являются волны когерентными или нет. Когерентными являются волны с одинаковыми частотами и неизменной во времени разностью начальных фаз. Интерференцией называется перераспределение интенсивности в пространстве при сложении когерентных волн. 2

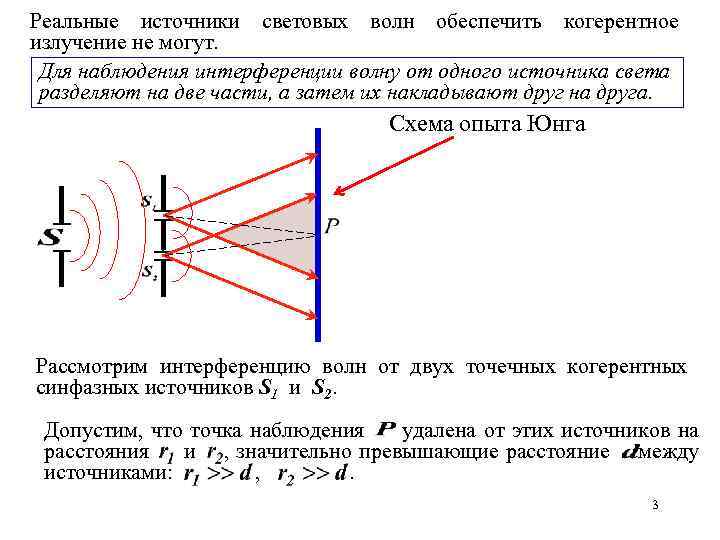Реальные источники световых волн обеспечить когерентное излучение не могут. Для наблюдения интерференции волну от одного источника света разделяют на две части, а затем их накладывают друг на друга. Схема опыта Юнга Рассмотрим интерференцию волн от двух точечных когерентных синфазных источников S 1 и S 2. Допустим, что точка наблюдения удалена от этих источников на расстояния и , значительно превышающие расстояние между источниками: , . 3

Уравнения этих колебаний в т. P имеют вид: Произведения и исполняют роль начальных фаз: Уравнение результирующего колебания: где или Амплитуда результирующего колебания зависит от расположения точки наблюдения относительно источников. В полученном выражении - разность хода волн. 4

Рассмотрим два предельных случая: 1. Пусть выполняется следующее условие: где Из выражения для амплитуды при этом следует: Такие точки называются максимумами интерференции. Условие максимумов: При такой разности хода волны имеют одинаковые фазы, следовательно, амплитуды складываются. 5

2. Пусть теперь выполняется такое условие: где Из выражения для амплитуды при этом следует: Если , то , результирующее колебание отсутствует. Такие точки называются минимумами интерференции. Условие минимумов: При такой разности хода волны имеют противоположные фазы, и поэтому частично или полностью гасят друга. 6

Интенсивность волн, приходящих в точку наблюдения: Суммарная интенсивность этих волн: Интенсивность волн в области максимумов: Следовательно, Интенсивность в областях максимумов больше суммы интенсивностей приходящих в эти области волн. Соответственно, интенсивность в областях минимумов меньше суммы интенсивностей приходящих в эти области волн. Эти результаты не противоречат закону сохранения энергии. При интерференции в зоне перекрытия волн происходит пространственное перераспределение энергии. Часть энергии из области минимумов энергии перемещается в области максимумов. 7

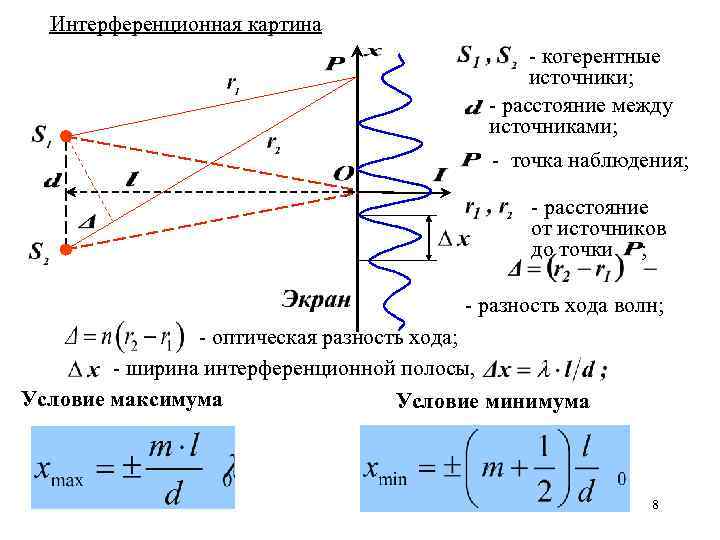Интерференционная картина - когерентные источники; - расстояние между источниками; - точка наблюдения; - расстояние от источников до точки ; - разность хода волн; - оптическая разность хода; - ширина интерференционной полосы, Условие максимума Условие минимума 8

Когерентность Однако монохроматическая волна, описываемая выражением представляет собой абстракцию Волны, излучаемые любыми независимыми источниками света, не могут быть монохроматическими и когерентными. Прерывистое излучение света атомами в виде отдельных коротких импульсов называется волновым цугом Средняя продолжительность одного цуга называется временем когерентности Расстояние называется длиной когерентности Для получения интерференционной картины разность хода световых волн должна быть меньше длины когерентности для используемого источника света Длина когерентности световой волны связана со степенью монохроматичности света, равной отношению , где – конечный интервал длин волн, интерференция которых наблюдается. Эта связь выражается соотношением: 9

Методы получения интерференции Интерференция, получаемая делением волнового фронта Самостоятельно -Метод Юнга -Бипризма Френеля -Бизеркала Френеля 10

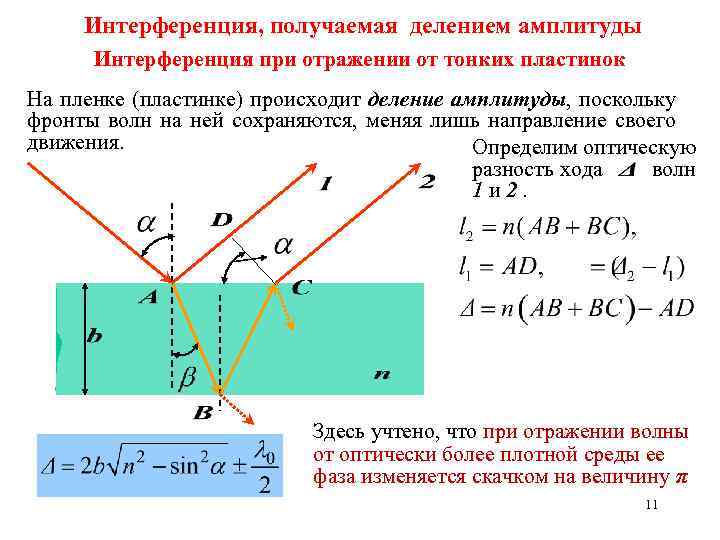Интерференция, получаемая делением амплитуды Интерференция при отражении от тонких пластинок На пленке (пластинке) происходит деление амплитуды, поскольку фронты волн на ней сохраняются, меняя лишь направление своего движения. Определим оптическую разность хода волн 1 и 2. Здесь учтено, что при отражении волны от оптически более плотной среды ее фаза изменяется скачком на величину π 11

Тогда условие временной когерентности можно записать в виде: или - удвоенная толщина пластинки должна быть меньше длины когерентности. Интерференционная картина будет наблюдаться в виде системы полос Каждая полоса будет образована лучами, падающими на пластинку под одинаковым углом. В связи с этим интерференционные полосы называются полосами равного наклона. Локализованы полосы равного наклона в бесконечности. Интерференцию можно наблюдать и в проходящем свете. Особенность – в проходящем свете потери полуволны не будет, оптическая разность хода волн для проходящего и отраженного света отличается на. В связи с этим, например, максимуму интерференции в отраженном свете соответствует минимум в проходящем свете. 12

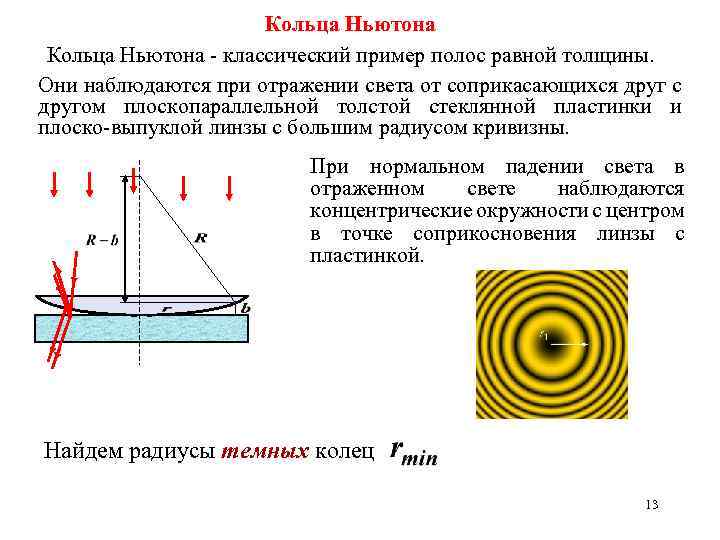Кольца Ньютона - классический пример полос равной толщины. Они наблюдаются при отражении света от соприкасающихся друг с другом плоскопараллельной толстой стеклянной пластинки и плоско-выпуклой линзы с большим радиусом кривизны. При нормальном падении света в отраженном свете наблюдаются концентрические окружности с центром в точке соприкосновения линзы с пластинкой. Найдем радиусы темных колец 13

При нормальном падении света угол равен нулю, (воздушный зазор). (полуволна "теряется" при отражении от пластинки) Условие минимумов Пренебрежем 14

Найдем радиусы светлых колец (максимумов) Рассмотрим случай, m = 0 Это физически бессмысленно. Следовательно, в центре будет наблюдаться темное пятно, минимум 15

n 1 n 2 n 3 Можно и в отражённом свете получить в центре светлое пятно, если пространство между линзой и пластинкой заполнено веществом, с показателем преломления: n 3 > n 2 > n 1 Применение интерференции Интерферометры Просветление оптики Для воздуха n 0 1 1 1' 2' n 0 n nc 2 d 16

Для нормального падения условие минимума n d – оптическая толщина плёнки Обычно порядок интерференции принимают m = 0 Оптическая толщина равна 0/4 0 = 0, 55 мкм 17

Дифракция световых волн Дифракцией называется совокупность явлений, наблюдаемых при распространении света в среде с резкими неоднородностями, размеры которых сравнимы с длиной волны (края экранов, малые отверстия и т. д. ). Дифракция приводит к огибанию световыми волнами препятствий и проникновению света в область геометрической тени. Интерференция и дифракция - явления одной физической природы. Оба заключаются в перераспределении светового потока в результате суперпозиции волн. Принято интерференцией называть перераспределение интенсивности, возникающее в результате суперпозиции волн от конечного числа дискретных когерентных источников. Если же складываются волны от бесконечного числа непрерывно распределенных когерентных источников – это дифракция. Различают два вида дифракции: - дифракция Френеля – дифракция в сходящихся лучах; - дифракция Фраунгофера (дифракция в параллельных лучах) источник света и точка наблюдения расположены от препятствия далеко. Падающие на препятствие и идущие в точку наблюдения лучи образуют практически параллельные пучки. 18

Принцип Гюйгенса-Френеля 1. Принцип Гюйгенса: каждую точку фронта волны можно рассматривать как источник вторичных волн. Френель развил этот принцип. 2. Все вторичные источники фронта волны, исходящие из одного источника, когерентны между собой. 3. Равные по площади участки волновой поверхности излучают равные интенсивности (мощности). 4. Каждый вторичный источник излучает свет преимущественно в направлении внешней нормали к волновой поверхности в этой точке. 5. Для вторичных источников справедлив принцип суперпозиции волн. Геометрическая тень 19

Для определения напряженности E в точке P, лежащей перед некоторой поверхностью S, надо найти колебания, приходящие в эту точку от всех элементов d. S поверхности S и затем сложить их с учетом амплитуд и фаз Суммировать (интегрировать) амплитуды элементарных колебаний, приходящих в точку , в общем случае сложно. Метод зон Френеля Волновая поверхность разбивается на кольцевые зоны так, чтобы расстояния от краев каждой зоны до точки Р отличались друг от друга на половину длины волны λ/2. Обладающие таким свойством зоны называются зонами Френеля. b - расстояние от вершины волновой 20 поверхности до точки P.

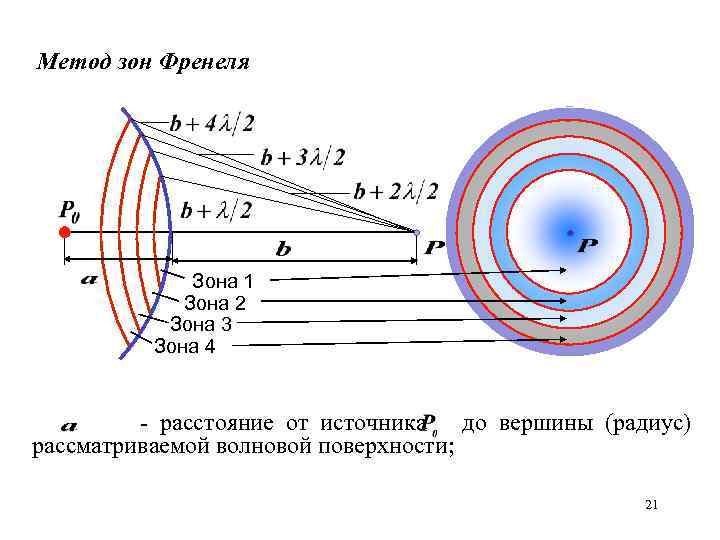Метод зон Френеля Зона 1 Зона 2 Зона 3 Зона 4 - расстояние от источника до вершины (радиус) рассматриваемой волновой поверхности; 21

Радиусы зон Френеля: Площадь - ой зоны равна: Полученное выражение не зависит от. Это значит, что при малых площади зон Френеля одинаковы. С увеличением номера зоны возрастает угол между нормалью к волновой поверхности и точкой наблюдения P, т. е. интенсивность излучения в направлении точки P также уменьшается. Амплитуда результирующего колебания в точке P Фазы колебаний, возбуждаемых соседними зонами, различаются на π 22

Оценки показывают, что радиус первой зоны Френеля очень мал. Это означает, что световой поток распространяется от будто внутри очень узкого канала , т. е. прямолинейно. к как Таким образом, принцип Гюйгенса – Френеля объясняет прямолинейное распространение света в однородной среде. Некоторые дополнительные выводы из принципа Гюйгенса – Френеля: 1. Если закрыть все зоны, кроме первой, то амплитуда в точке. увеличится по сравнению с полностью открытым волновым фронтом в два раза , а интенсивность в четыре раза. 2. Если отверстие в преграде открывает для точки две зоны Френеля, интенсивность в этой точке падает практически до нуля. . 23

Дифракция в сходящихся лучах (дифракция Френеля) Дифракция Френеля наблюдается в том случае, когда на препятствие падает сферическая или плоская волна, а экран, на котором наблюдается дифракционная картина, находится на конечном расстоянии от препятствия. Дифракция на круглом отверстии. Освещенность в т. Р зависит от числа зон Френеля, которые укладываются на открытой части волновой поверхности в плоскости отверстия. Это число может быть четным или нечетным в зависимости от размера отверстия и длины волны. Экран 24

Дифракция в сходящихся лучах (дифракция Френеля). Амплитуда результирующего колебания, возбуждаемого в точке. всеми зонами, равна С учетом принятого ранее допущения это выражение примет вид Знак «+» в этом выражении соответствует нечетным, « Экран – » - четным. Если отверстие открывает нечетное число зон Френеля, то в точке Р наблюдается максимум, если четное – то минимум. Если отверстие открывает только одну зону Френеля, то в точке будет максимальная интенсивность. Наименьшая интенсивность соответствует двум открытым зонам Френеля. 25

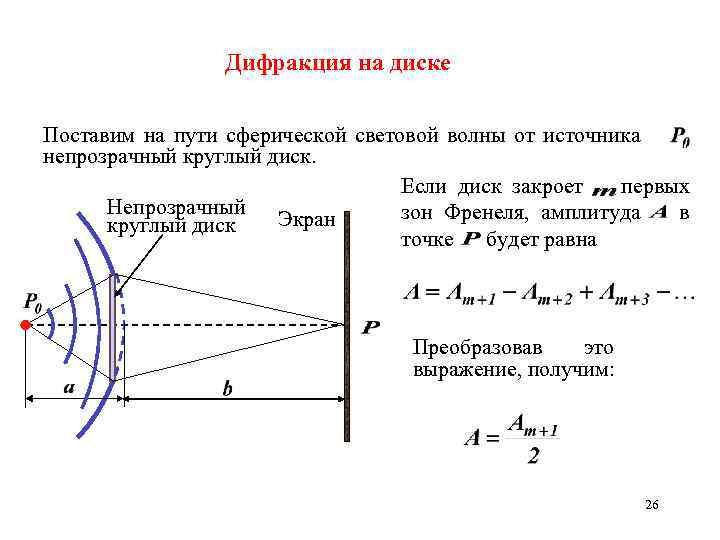Дифракция на диске Поставим на пути сферической световой волны от источника. непрозрачный круглый диск. Если диск закроет первых Непрозрачный зон Френеля, амплитуда в Экран круглый диск точке будет равна Преобразовав это выражение, получим: 26

Следовательно, в точке всегда наблюдается максимум (светлое пятно), соответствующий половине действия первой открытой зоны Френеля. Центральный максимум окружен концентричными с ним темными и светлыми кольцами, а интенсивность в максимумах убывает с ростом расстояния от центра картины. В результате интенсивность центрального максимума уменьшается с увеличением размеров диска. 27

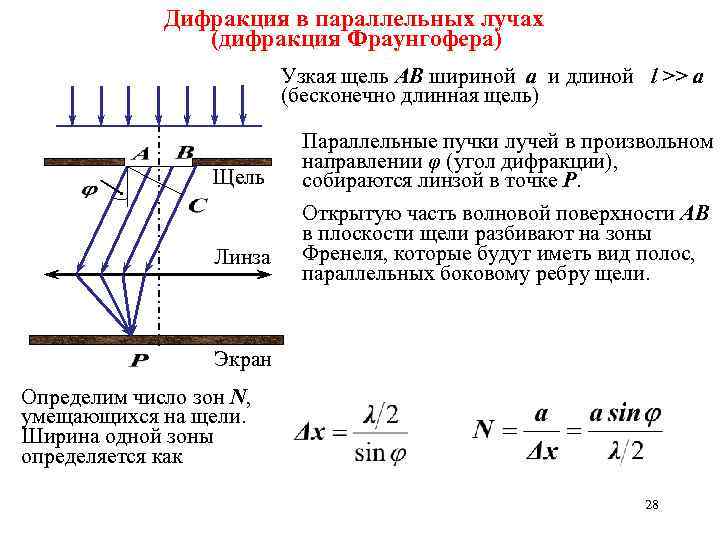Дифракция в параллельных лучах (дифракция Фраунгофера) Узкая щель АВ шириной а и длиной l >> a (бесконечно длинная щель) Щель Линза Параллельные пучки лучей в произвольном направлении φ (угол дифракции), собираются линзой в точке P. Открытую часть волновой поверхности АВ в плоскости щели разбивают на зоны Френеля, которые будут иметь вид полос, параллельных боковому ребру щели. Экран Определим число зон N, умещающихся на щели. Ширина одной зоны определяется как 28

Колебания, возбуждаемые в точке P двумя соседними зонами, равны по амплитуде и противоположны по фазе Дифракционный минимум наблюдается тогда, когда число зон Френеля в плоскости щели четное Дифракционный максимум наблюдается тогда, когда число зон Френеля в плоскости щели нечетное В направлении φ = 0 наблюдается центральный дифракционный максимум 29

Дифракционный спектр (зависимость распределения интенсивности на экране от угла дифракции) Щель Линза Экран Основная часть световой энергии сосредоточена в центральном максимуме. С увеличением угла дифракции интенсивность побочных максимумов резко уменьшается. 30

С уменьшением ширины щели центральный максимум расширяется Чем меньше a , тем больше φ и шире центральный максимум С увеличением ширины щели (a > λ) дифракционные полосы становятся уже и ярче, а число полос больше. При a >> λ в центре получается резкое изображение источника света (прямолинейное распространение света). При уменьшении ширины щели вся дифракционная картина расширяется, расплывается Интенсивность света пропорциональна квадрату амплитуды I A 2. Интенсивности максимумов соотносятся между собой следующим образом 31

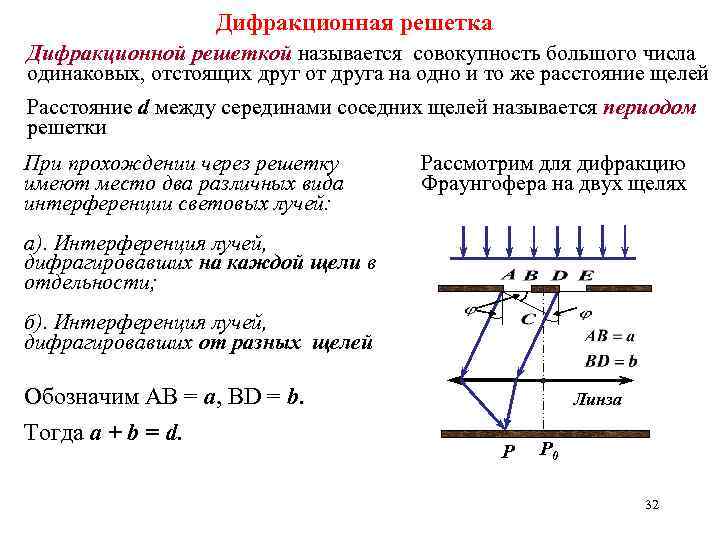Дифракционная решетка Дифракционной решеткой называется совокупность большого числа одинаковых, отстоящих друг от друга на одно и то же расстояние щелей Расстояние d между серединами соседних щелей называется периодом решетки При прохождении через решетку имеют место два различных вида интерференции световых лучей: Рассмотрим для дифракцию Фраунгофера на двух щелях а). Интерференция лучей, дифрагировавших на каждой щели в отдельности; б). Интерференция лучей, дифрагировавших от разных щелей Обозначим AB = a, BD = b. Тогда a + b = d. Линза P P 0 32

Минимумы, соответствующие дифракции на одной щели, останутся минимумами и при дифракции на двух и более щелях Это главные минимумы Из-за условие б, возникнут дополнительные минимумы Это будут направления, которым соответствует разность хода лучей , и т. д. Такие направления определяются условием Условие дополнительных минимумов 33

Главные максимумы, определяются условиями Для двух щелей дифракционная картина определяется условиями: главные минимумы: дополнительные минимумы: главные максимумы: 0, 34

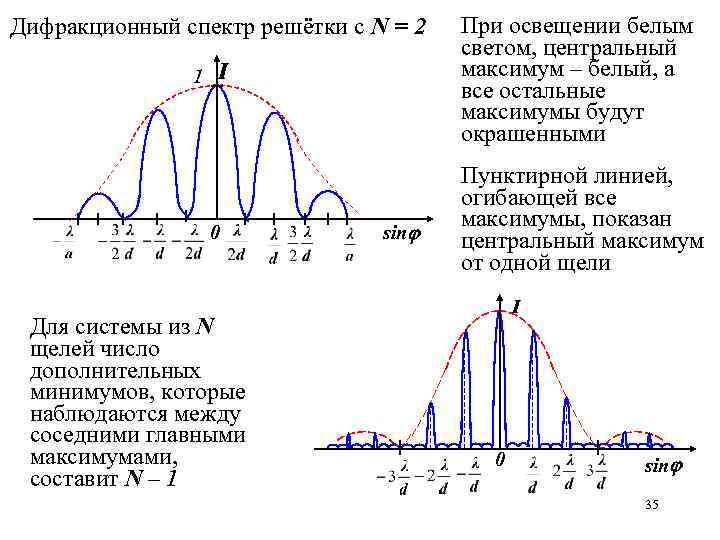Дифракционный спектр решётки с N = 2 1 I 0 Для системы из N щелей число дополнительных минимумов, которые наблюдаются между соседними главными максимумами, составит N – 1 sin При освещении белым светом, центральный максимум – белый, а все остальные максимумы будут окрашенными Пунктирной линией, огибающей все максимумы, показан центральный максимум от одной щели I 0 sin 35

Спектральное разложение Разрешающая способность решетки Условие главных максимумов дифракционной решетки содержит длину волны λ. Если на решетку падает белый свет, то при отличном от нуля значении m разным длинам волн будут соответствовать сдвинутые друг относительно друга максимумы. Каждому значению m ≠ 0 соответствует спектр, который начинается с фиолетовой полосы, и заканчивается красной Дифракционная решетка позволяет установить спектральный состав направленного на нее излучения и потому представляет собой спектральный прибор. В центральном максимуме спектральное разложение отсутствует. 36

ПОЛЯРИЗАЦИЯ СВЕТА Естественный и поляризованный свет - это суммарное излучение множества атомов, поэтому естественный (неполяризованный) свет характеризуется множеством равновероятных ориентаций светового вектора. Свет, в котором колебания светового вектора каким-либо образом упорядочены, называется поляризованным. Если колебания вектора происходят только в одной плоскости, проходящей через луч, то это плоско(или линейно-) поляризованная волна. Плоскость, в которой колеблется вектор поляризации. , называется плоскостью Если конец вектора в какой-то точке среды описывает эллипс или круг, то такую волну называют эллиптически поляризованной или поляризованной по кругу. 37

Из естественного света можно получить плоско-поляризованный свет с помощью поляризаторов. Они свободно пропускают колебания светового вектора, параллельные плоскости, которую называют плоскостью пропускания поляризатора. Колебания, перпендикулярные этой плоскости, задерживаются полностью или частично O 1 O 2 Iест Интенсивность света, прошедшего через один кристалл уменьшится в два раза I T 1 T 2 Помимо естественного и плоско-поляризованного света существует еще промежуточный случай – это частично-поляризованный свет Степень поляризации 38

Закон Малюса Поляризаторы можно использовать и в качестве анализаторов – устройств для определения характера и степени поляризации интересующего нас света На анализатор падает плоско-поляризованный свет, вектор которого составляет угол φ с плоскостью пропускания анализатора P. Анализатор пропускает только ту составляющую вектора , которая параллельна плоскости пропускания P, т. е. Интенсивность света пропорциональна квадрату модуля светового вектора ( ) – интенсивность падающего на анализатор плоско-поляризованного света Это соотношение носит название закона Малюса 39

В естественном свете все значения равновероятны и среднее значение Поэтому интенсивность естественного света, прошедшего поляризатор, уменьшается в два раза I 0 П I' А I Плоскости поляризации образуют угол Согласно закону Малюса Это без учёта поглощения света в кристалле при = 0 I = 0 при Скрещенные поляризаторы свет не пропускают 40

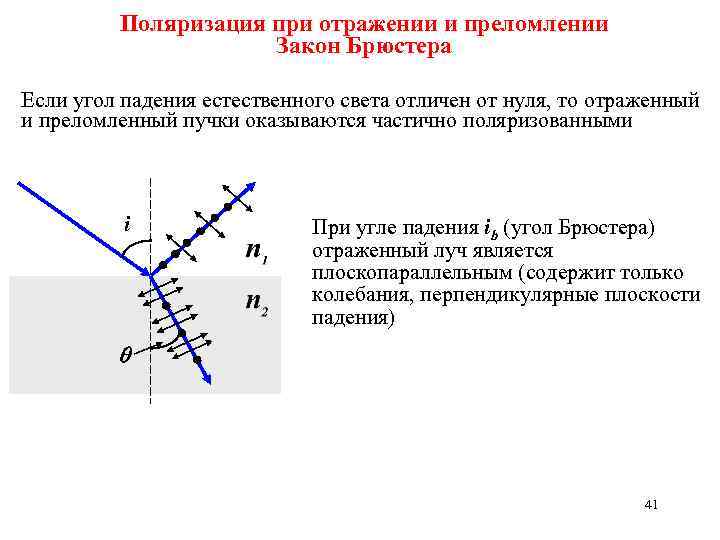Поляризация при отражении и преломлении Закон Брюстера Если угол падения естественного света отличен от нуля, то отраженный и преломленный пучки оказываются частично поляризованными i При угле падения ib (угол Брюстера) отраженный луч является плоскопараллельным (содержит только колебания, перпендикулярные плоскости падения) 41

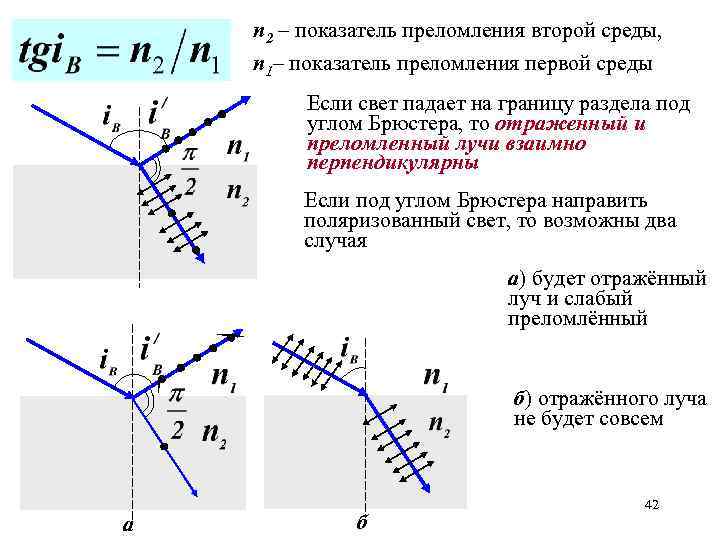n 2 – показатель преломления второй среды, n 1– показатель преломления первой среды Если свет падает на границу раздела под углом Брюстера, то отраженный и преломленный лучи взаимно перпендикулярны Если под углом Брюстера направить поляризованный свет, то возможны два случая а) будет отражённый луч и слабый преломлённый б) отражённого луча не будет совсем а б 42