ВОЛНОВАЯ ОПТИКА 1




















 ВОЛНОВАЯ ОПТИКА 1
ВОЛНОВАЯ ОПТИКА 1
 Coдержание предыдущей лекции Интерференция световых волн Условия интерференции. Интерференционная картина, созданная двумя когерентными источниками света. Распределение интенсивности на интерференционной картине, созданной двумя щелями. Изменение фазы в результате отражения света. Интерференция в тонких пленках. 2
Coдержание предыдущей лекции Интерференция световых волн Условия интерференции. Интерференционная картина, созданная двумя когерентными источниками света. Распределение интенсивности на интерференционной картине, созданной двумя щелями. Изменение фазы в результате отражения света. Интерференция в тонких пленках. 2
 Контрольный вопрос В лаборатории произошел инцидент, при котором две разные жидкости попали в воду. Жидкости оказались несмешиваемыми с водой и образовали на ее поверхности две очень тонкие пленки. В отраженном свете одна из пленок выглядит светлой, а другая темной. Какое из нижеперечисленных утверждений верно: а) показатель преломления темной пленки больше, чем у воды, б) показатель преломления темной пленки меньше, чем у воды, в) показатель преломления темной пленки равен показателю преломления воды, г) показатель преломления темной пленки меньше, чем таковой у светлой пленки. У одной из пленок показатель преломления выше, чем у воды, у другой ниже. В случае пленки с более высоким показателем преломления при отражении волны от ее верхней поверхности происходит сдвиг по фазе на 180º. Такого сдвига не происходит при отражении волны от нижней поверхности пленки, поскольку показатель преломления воды, на которой располагается пленка, ниже, чем у самой пленки. Таким образом, волны, отраженные от верхней и нижней поверхностей пленки накладываются в противофазе и интерферируют деструктивно. 3
Контрольный вопрос В лаборатории произошел инцидент, при котором две разные жидкости попали в воду. Жидкости оказались несмешиваемыми с водой и образовали на ее поверхности две очень тонкие пленки. В отраженном свете одна из пленок выглядит светлой, а другая темной. Какое из нижеперечисленных утверждений верно: а) показатель преломления темной пленки больше, чем у воды, б) показатель преломления темной пленки меньше, чем у воды, в) показатель преломления темной пленки равен показателю преломления воды, г) показатель преломления темной пленки меньше, чем таковой у светлой пленки. У одной из пленок показатель преломления выше, чем у воды, у другой ниже. В случае пленки с более высоким показателем преломления при отражении волны от ее верхней поверхности происходит сдвиг по фазе на 180º. Такого сдвига не происходит при отражении волны от нижней поверхности пленки, поскольку показатель преломления воды, на которой располагается пленка, ниже, чем у самой пленки. Таким образом, волны, отраженные от верхней и нижней поверхностей пленки накладываются в противофазе и интерферируют деструктивно. 3
 Coдержание сегодняшней лекции Интерференция световых волн Интерференция в тонких пленках. Зоны Френеля (самостоятельно). Фазовое сложение волн. Интерферометр Майкельсона. Дифракция Явление дифракции. Составляющие дифракционной картины. Дифракция Фраунгофера. Распределение интенсивности на дифракционной картине. 4
Coдержание сегодняшней лекции Интерференция световых волн Интерференция в тонких пленках. Зоны Френеля (самостоятельно). Фазовое сложение волн. Интерферометр Майкельсона. Дифракция Явление дифракции. Составляющие дифракционной картины. Дифракция Фраунгофера. Распределение интенсивности на дифракционной картине. 4
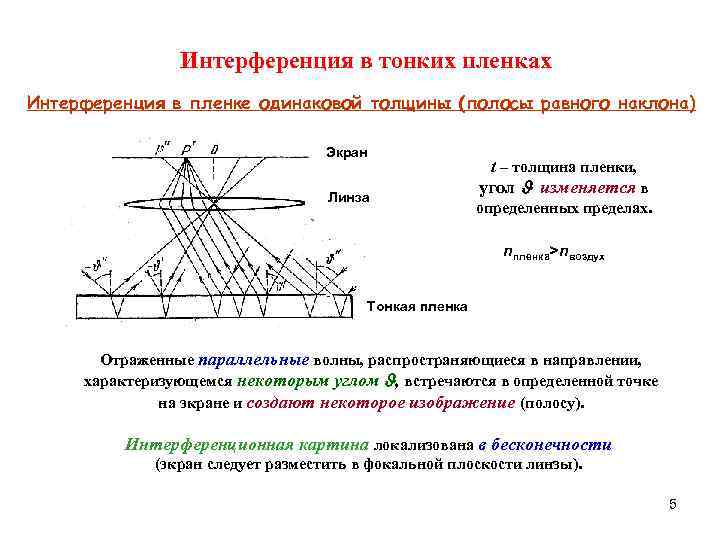
 Интерференция в тонких пленках Интерференция в пленке одинаковой толщины (полосы равного наклона) Экран t – толщина пленки, Линза угол изменяется в определенных пределах. nпленка>nвоздух Тонкая пленка Отраженные параллельные волны, распространяющиеся в направлении, характеризующемся некоторым углом , встречаются в определенной точке на экране и создают некоторое изображение (полосу). Интерференционная картина локализована в бесконечности (экран следует разместить в фокальной плоскости линзы). 5
Интерференция в тонких пленках Интерференция в пленке одинаковой толщины (полосы равного наклона) Экран t – толщина пленки, Линза угол изменяется в определенных пределах. nпленка>nвоздух Тонкая пленка Отраженные параллельные волны, распространяющиеся в направлении, характеризующемся некоторым углом , встречаются в определенной точке на экране и создают некоторое изображение (полосу). Интерференционная картина локализована в бесконечности (экран следует разместить в фокальной плоскости линзы). 5
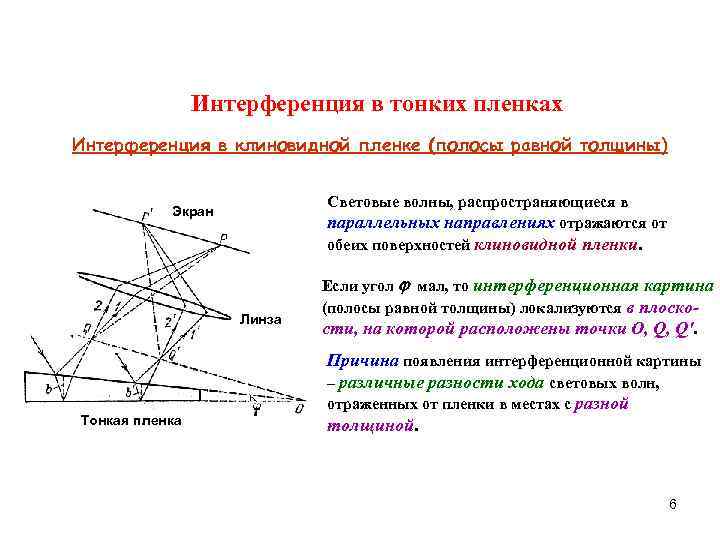
 Интерференция в тонких пленках Интерференция в клиновидной пленке (полосы равной толщины) Световые волны, распространяющиеся в Экран параллельных направлениях отражаются от обеих поверхностей клиновидной пленки. Если угол мал, то интерференционная картина (полосы равной толщины) локализуются в плоско- Линза сти, на которой расположены точки O, Q, Q'. Причина появления интерференционной картины – различные разности хода световых волн, отраженных от пленки в местах с разной Тонкая пленка толщиной. 6
Интерференция в тонких пленках Интерференция в клиновидной пленке (полосы равной толщины) Световые волны, распространяющиеся в Экран параллельных направлениях отражаются от обеих поверхностей клиновидной пленки. Если угол мал, то интерференционная картина (полосы равной толщины) локализуются в плоско- Линза сти, на которой расположены точки O, Q, Q'. Причина появления интерференционной картины – различные разности хода световых волн, отраженных от пленки в местах с разной Тонкая пленка толщиной. 6
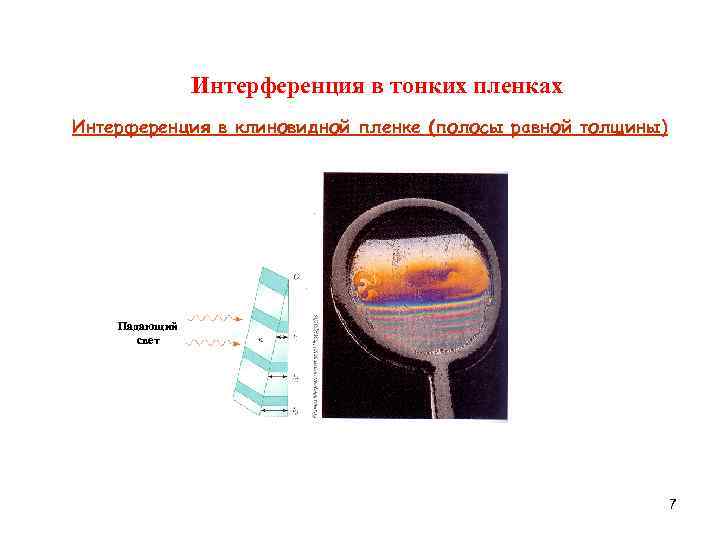
 Интерференция в тонких пленках Интерференция в клиновидной пленке (полосы равной толщины) Падающий свет 7
Интерференция в тонких пленках Интерференция в клиновидной пленке (полосы равной толщины) Падающий свет 7
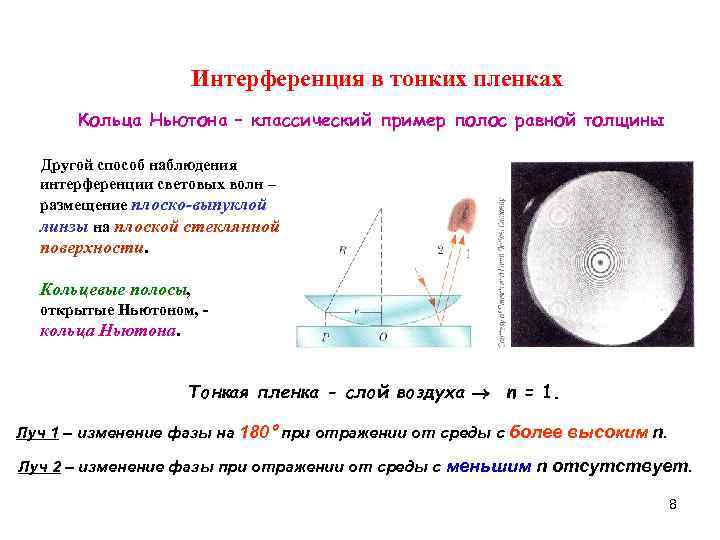
 Интерференция в тонких пленках Кольца Ньютона – классический пример полос равной толщины Другой способ наблюдения интерференции световых волн – размещение плоско-выпуклой линзы на плоской стеклянной поверхности. Кольцевые полосы, открытые Ньютоном, - кольца Ньютона. Тонкая пленка - слой воздуха n = 1. Луч 1 – изменение фазы на 180 при отражении от среды c более высоким n. Луч 2 – изменение фазы при отражении от среды с меньшим n отсутствует. 8
Интерференция в тонких пленках Кольца Ньютона – классический пример полос равной толщины Другой способ наблюдения интерференции световых волн – размещение плоско-выпуклой линзы на плоской стеклянной поверхности. Кольцевые полосы, открытые Ньютоном, - кольца Ньютона. Тонкая пленка - слой воздуха n = 1. Луч 1 – изменение фазы на 180 при отражении от среды c более высоким n. Луч 2 – изменение фазы при отражении от среды с меньшим n отсутствует. 8
 Интерференция в тонких пленках Кольца Ньютона Условие конструктивной Условие деструктивной интерференции (максимумов) интерференции (минимумов) 2 t =(m+1/2) λ, (m = 0, 1, 2, …). 2 t =mλ, (m = 0, 1, 2, …). В точке контакта O темно: 1) разность хода лучей отсутствует; 2) общее изменение фазы равно 180 и связано с отражением. Каковы радиусы колец Ньютона? R Если свет падает нормально на поверхность линзы, то R-t r t Оптическая разность хода 9
Интерференция в тонких пленках Кольца Ньютона Условие конструктивной Условие деструктивной интерференции (максимумов) интерференции (минимумов) 2 t =(m+1/2) λ, (m = 0, 1, 2, …). 2 t =mλ, (m = 0, 1, 2, …). В точке контакта O темно: 1) разность хода лучей отсутствует; 2) общее изменение фазы равно 180 и связано с отражением. Каковы радиусы колец Ньютона? R Если свет падает нормально на поверхность линзы, то R-t r t Оптическая разность хода 9
 Интерференция в тонких пленках Кольца Ньютона Максимальная Mинимальная интенсивность, если Радиусы светлых колец Радиусы темных колец Радиусы колец (нечетные m' для светлых колец и четные m' для темных колец) Важное применение: контроль качества оптических линз. Ассиметричная интерференционная картина отражает несовершенства линзы в приборе для наблюдения колец Ньютона. 10
Интерференция в тонких пленках Кольца Ньютона Максимальная Mинимальная интенсивность, если Радиусы светлых колец Радиусы темных колец Радиусы колец (нечетные m' для светлых колец и четные m' для темных колец) Важное применение: контроль качества оптических линз. Ассиметричная интерференционная картина отражает несовершенства линзы в приборе для наблюдения колец Ньютона. 10
 Фазовое сложение волн Ранее нами исследовался аналитически результат интерференции (суперпозиции) двух волн. Аналитические расчеты становятся затруднительными, если необходимо сложить амплитуды нескольких волн. Графическая процедура сложения амплитуд нескольких волн – фазовое сложение волн. 11
Фазовое сложение волн Ранее нами исследовался аналитически результат интерференции (суперпозиции) двух волн. Аналитические расчеты становятся затруднительными, если необходимо сложить амплитуды нескольких волн. Графическая процедура сложения амплитуд нескольких волн – фазовое сложение волн. 11
 Фазовое сложение волн Фазовая диаграмма Закон векторной алгебры: волнового колебания Сдвиг по фазе результирующего фазового вектора ER по отношению к исходному фазовому вектору E 0 равен . Из геометрических построений = / 2. 12
Фазовое сложение волн Фазовая диаграмма Закон векторной алгебры: волнового колебания Сдвиг по фазе результирующего фазового вектора ER по отношению к исходному фазовому вектору E 0 равен . Из геометрических построений = / 2. 12
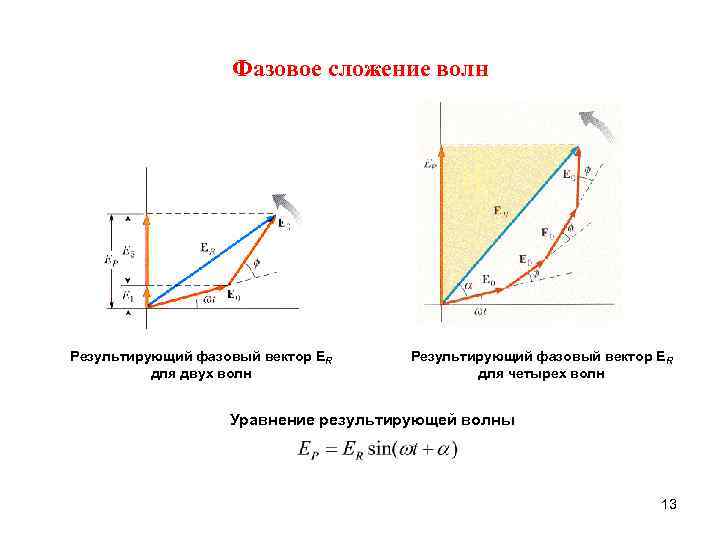
 Фазовое сложение волн Результирующий фазовый вектор ER для двух волн для четырех волн Уравнение результирующей волны 13
Фазовое сложение волн Результирующий фазовый вектор ER для двух волн для четырех волн Уравнение результирующей волны 13
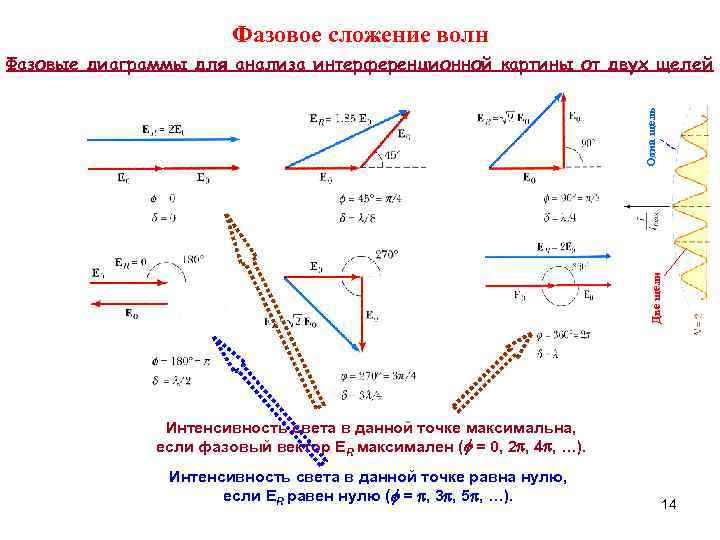
 Фазовое сложение волн Фазовые диаграммы для анализа интерференционной картины от двух щелей Одна щель Две щели Интенсивность света в данной точке максимальна, если фазовый вектор ER максимален ( = 0, 2 , 4 , …). Интенсивность света в данной точке равна нулю, если ER равен нулю ( = , 3 , 5 , …). 14
Фазовое сложение волн Фазовые диаграммы для анализа интерференционной картины от двух щелей Одна щель Две щели Интенсивность света в данной точке максимальна, если фазовый вектор ER максимален ( = 0, 2 , 4 , …). Интенсивность света в данной точке равна нулю, если ER равен нулю ( = , 3 , 5 , …). 14
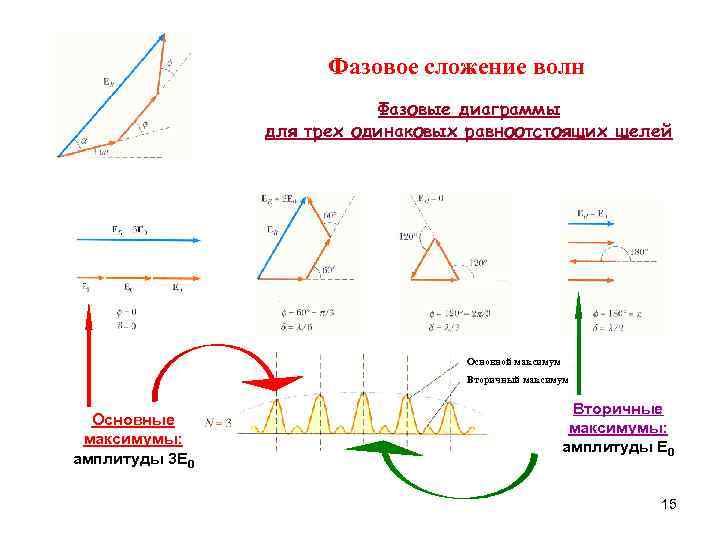
 Фазовое сложение волн Фазовые диаграммы для трех одинаковых равноотстоящих щелей Основной максимум Вторичный максимум Вторичные Основные максимумы: амплитуды E 0 амплитуды 3 E 0 15
Фазовое сложение волн Фазовые диаграммы для трех одинаковых равноотстоящих щелей Основной максимум Вторичный максимум Вторичные Основные максимумы: амплитуды E 0 амплитуды 3 E 0 15
 Фазовое сложение волн Первичные максимумы соответствуют точкам на фазовой диаграмме, в которых результирующая величина напряженности электрического поля максимальна. Все фазовые векторы имеют одно и то же направление. Волны, распространяющиеся от всех щелей, складываются в фазе и усиливают друга. Вторичные максимумы – соответствуют точкам на фазовой диаграмме, в которых волны, распространяющиеся от некоторых щелей, полностью уничтожают волны, распространяющиеся от других щелей. Только те волны, которые не уничтожаются, дают вклад в результирующую волну. 16
Фазовое сложение волн Первичные максимумы соответствуют точкам на фазовой диаграмме, в которых результирующая величина напряженности электрического поля максимальна. Все фазовые векторы имеют одно и то же направление. Волны, распространяющиеся от всех щелей, складываются в фазе и усиливают друга. Вторичные максимумы – соответствуют точкам на фазовой диаграмме, в которых волны, распространяющиеся от некоторых щелей, полностью уничтожают волны, распространяющиеся от других щелей. Только те волны, которые не уничтожаются, дают вклад в результирующую волну. 16
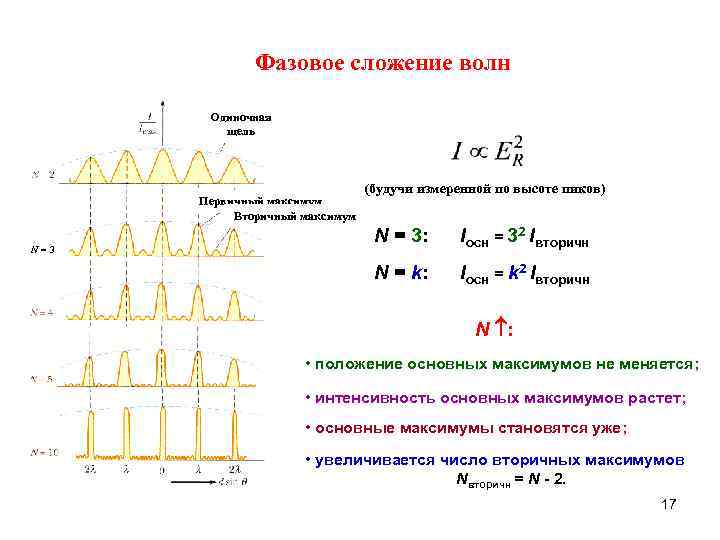
 Фазовое сложение волн Одиночная щель (будучи измеренной по высоте пиков) Первичный максимум Вторичный максимум N = 3: Iосн = 32 Iвторичн N=3 N = k: Iосн = k 2 Iвторичн N : • положение основных максимумов не меняется; • интенсивность основных максимумов растет; • основные максимумы становятся уже; • увеличивается число вторичных максимумов Nвторичн = N - 2. 17
Фазовое сложение волн Одиночная щель (будучи измеренной по высоте пиков) Первичный максимум Вторичный максимум N = 3: Iосн = 32 Iвторичн N=3 N = k: Iосн = k 2 Iвторичн N : • положение основных максимумов не меняется; • интенсивность основных максимумов растет; • основные максимумы становятся уже; • увеличивается число вторичных максимумов Nвторичн = N - 2. 17
 Интерферометр Майкельсона Американский физик A. A. Майкельсон (1852 -1931): • разделил пучок света на две части; • наложил эти части для формирования интерференционной картины. Зеркало M 0 разделяет пучок, отражая 50% и пропуская 50% монохроматического света, распространяющегося от источника. L 1 и L 2 – различные пути, пройденные лучами 1 и Источник 2 перед тем как они отражаются зеркалами M 1 и света M 2 и накладываются друг на друга на зеркале M 0. Если M 1 перемещается в направлении к M 0, то положения максимумов и минимумов на Зрительная труба интерференционной картине изменяются. Эти изменения связаны с дополнительной разностью хода и соответствующей разностью фаз лучей. Такой подход может быть использован для измерения длины волны света. 18
Интерферометр Майкельсона Американский физик A. A. Майкельсон (1852 -1931): • разделил пучок света на две части; • наложил эти части для формирования интерференционной картины. Зеркало M 0 разделяет пучок, отражая 50% и пропуская 50% монохроматического света, распространяющегося от источника. L 1 и L 2 – различные пути, пройденные лучами 1 и Источник 2 перед тем как они отражаются зеркалами M 1 и света M 2 и накладываются друг на друга на зеркале M 0. Если M 1 перемещается в направлении к M 0, то положения максимумов и минимумов на Зрительная труба интерференционной картине изменяются. Эти изменения связаны с дополнительной разностью хода и соответствующей разностью фаз лучей. Такой подход может быть использован для измерения длины волны света. 18
 Интерферометр Майкельсона Лазерный интерферометр обсерватории в Ричлэнде (штат Вашингтон), предназначенный для обнаружения гравитационных волн. Видны два перпендикулярных плеча интерферометра. 19
Интерферометр Майкельсона Лазерный интерферометр обсерватории в Ричлэнде (штат Вашингтон), предназначенный для обнаружения гравитационных волн. Видны два перпендикулярных плеча интерферометра. 19
 Дифракция 20
Дифракция 20
 Явление дифракции Свет с длиной волны сравнимой или больше чем ширина щели после прохождения через щель распространяется во всех возможных направлениях. Щель действует как точечный источник света, испускающий волны, распространяющиеся в область геометрической тени за барьером. Это явление называется дифракцией и может быть объяснено только в рамках волновой модели света. Волны с иными длинами, такие как волны звука или волны на воде, также обладают свойством распространяться во всех возможных направлениях, что особенно наглядно иллюстрируется в случаях прохождения этих волн сквозь щели или вблизи края непрозрачных препятствий. 21
Явление дифракции Свет с длиной волны сравнимой или больше чем ширина щели после прохождения через щель распространяется во всех возможных направлениях. Щель действует как точечный источник света, испускающий волны, распространяющиеся в область геометрической тени за барьером. Это явление называется дифракцией и может быть объяснено только в рамках волновой модели света. Волны с иными длинами, такие как волны звука или волны на воде, также обладают свойством распространяться во всех возможных направлениях, что особенно наглядно иллюстрируется в случаях прохождения этих волн сквозь щели или вблизи края непрозрачных препятствий. 21
 Составляющие дифракционной картины Ожидания: свет, проходящий через узкую щель, должен оставлять яркий широкий след на экране. Действительность: дифракционная картина состоит из последовательности светлых и темных областей. Дифракционная картина от щели состоит из: • центрального максимума – широкой, интенсивной центральной полосы, • боковых или вторичных максимумов – ряда более узких, менее интенсивных дополнительных полос, • минимумов – ряда промежуточных темных полос. 22
Составляющие дифракционной картины Ожидания: свет, проходящий через узкую щель, должен оставлять яркий широкий след на экране. Действительность: дифракционная картина состоит из последовательности светлых и темных областей. Дифракционная картина от щели состоит из: • центрального максимума – широкой, интенсивной центральной полосы, • боковых или вторичных максимумов – ряда более узких, менее интенсивных дополнительных полос, • минимумов – ряда промежуточных темных полос. 22
 Дифракционные картины Дифракционная картина, связанная со светом, проходящим вблизи края непрозрачного препятствия Экран Источник Непрозрачное препятствие Над краем непрозрачного препятствия формируется дифракционная картина. 23
Дифракционные картины Дифракционная картина, связанная со светом, проходящим вблизи края непрозрачного препятствия Экран Источник Непрозрачное препятствие Над краем непрозрачного препятствия формируется дифракционная картина. 23
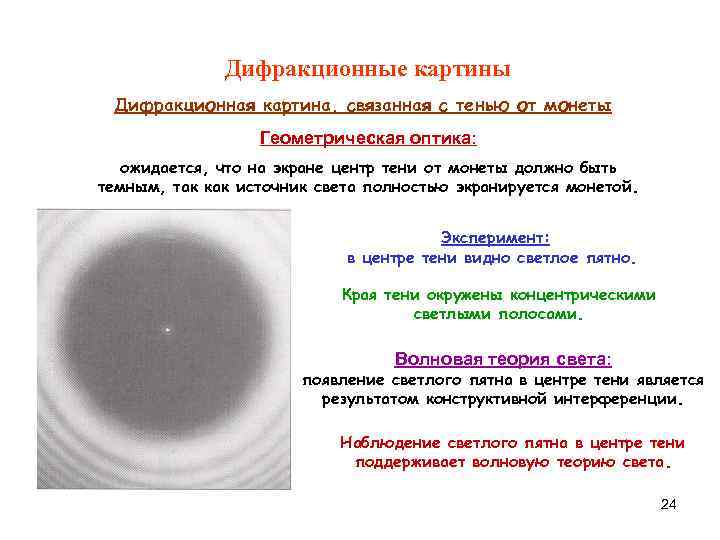
 Дифракционные картины Дифракционная картина, связанная с тенью от монеты Геометрическая оптика: ожидается, что на экране центр тени от монеты должно быть темным, так как источник света полностью экранируется монетой. Эксперимент: в центре тени видно светлое пятно. Края тени окружены концентрическими светлыми полосами. Волновая теория света: появление светлого пятна в центре тени является результатом конструктивной интерференции. Наблюдение светлого пятна в центре тени поддерживает волновую теорию света. 24
Дифракционные картины Дифракционная картина, связанная с тенью от монеты Геометрическая оптика: ожидается, что на экране центр тени от монеты должно быть темным, так как источник света полностью экранируется монетой. Эксперимент: в центре тени видно светлое пятно. Края тени окружены концентрическими светлыми полосами. Волновая теория света: появление светлого пятна в центре тени является результатом конструктивной интерференции. Наблюдение светлого пятна в центре тени поддерживает волновую теорию света. 24
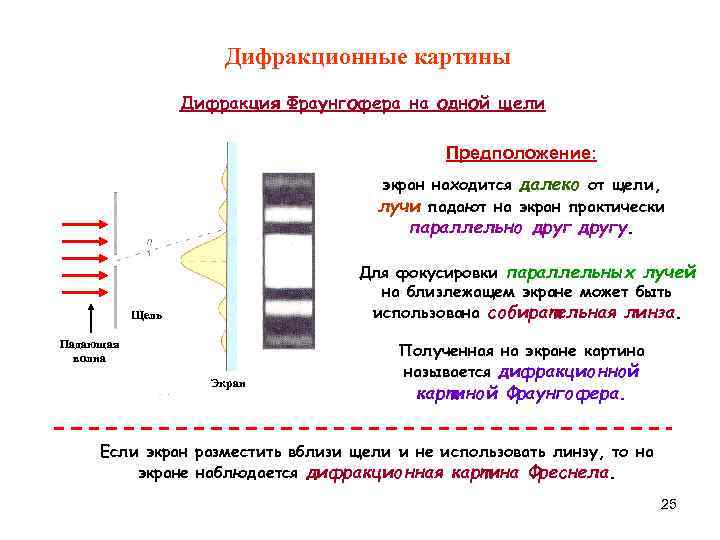
 Дифракционные картины Дифракция Фраунгофера на одной щели Предположение: экран находится далеко от щели, лучи падают на экран практически параллельно другу. Для фокусировки параллельных лучей на близлежащем экране может быть Щель использована собирательная линза. Падающая волна Полученная на экране картина называется дифракционной Экран картиной Фраунгофера. Если экран разместить вблизи щели и не использовать линзу, то на экране наблюдается дифракционная картина Фреснела. 25
Дифракционные картины Дифракция Фраунгофера на одной щели Предположение: экран находится далеко от щели, лучи падают на экран практически параллельно другу. Для фокусировки параллельных лучей на близлежащем экране может быть Щель использована собирательная линза. Падающая волна Полученная на экране картина называется дифракционной Экран картиной Фраунгофера. Если экран разместить вблизи щели и не использовать линзу, то на экране наблюдается дифракционная картина Фреснела. 25
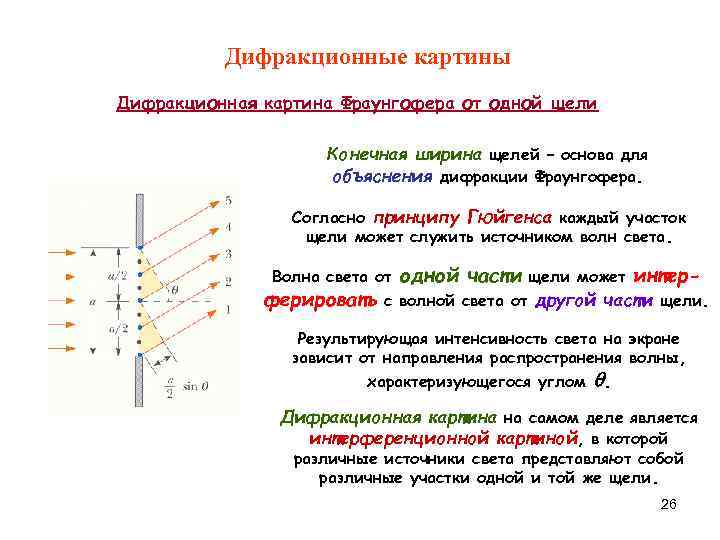
 Дифракционные картины Дифракционная картина Фраунгофера от одной щели Конечная ширина щелей – основа для объяснения дифракции Фраунгофера. Согласно принципу Гюйгенса каждый участок щели может служить источником волн света. Волна света от одной части щели может интер- ферировать с волной света от другой части щели. Результирующая интенсивность света на экране зависит от направления распространения волны, характеризующегося углом . Дифракционная картина на самом деле является интерференционной картиной, в которой различные источники света представляют собой различные участки одной и той же щели. 26
Дифракционные картины Дифракционная картина Фраунгофера от одной щели Конечная ширина щелей – основа для объяснения дифракции Фраунгофера. Согласно принципу Гюйгенса каждый участок щели может служить источником волн света. Волна света от одной части щели может интер- ферировать с волной света от другой части щели. Результирующая интенсивность света на экране зависит от направления распространения волны, характеризующегося углом . Дифракционная картина на самом деле является интерференционной картиной, в которой различные источники света представляют собой различные участки одной и той же щели. 26
 Дифракционные картины Анализ дифракционной картины Для удобства сначала разделим щель на две половины. Все волны находятся в фазе в момент покидания щели. Разность хода лучей 3 и 1 (4 и 2, 5 и 3) равна (a/2)sin. Если эта разность хода равна ровно /2 (разность фаз равна ), то две волны взаимно уничтожаются – деструктивная интерференция. Если волны от верхней половины щели интерферируют деструктивно с волнами от нижней половины щели, то 27
Дифракционные картины Анализ дифракционной картины Для удобства сначала разделим щель на две половины. Все волны находятся в фазе в момент покидания щели. Разность хода лучей 3 и 1 (4 и 2, 5 и 3) равна (a/2)sin. Если эта разность хода равна ровно /2 (разность фаз равна ), то две волны взаимно уничтожаются – деструктивная интерференция. Если волны от верхней половины щели интерферируют деструктивно с волнами от нижней половины щели, то 27
 Дифракционные картины Условия для деструктивной интерференции: Если щель разделена на четыре равные части, то на экране появляется темное пятно и Если щель разделена на шесть равных частей, то на экране появляется темное пятно и Обобщенное условие для деструктивной интерференции 28
Дифракционные картины Условия для деструктивной интерференции: Если щель разделена на четыре равные части, то на экране появляется темное пятно и Если щель разделена на шесть равных частей, то на экране появляется темное пятно и Обобщенное условие для деструктивной интерференции 28
 Дифракционные картины Распределение интенсивности sin темн = 2 / a sin темн = / a sin темн = - / a sin темн = -2 / a Экран Характерные черты дифракционной картины: • широкая центральная светлая полоса, • намного более слабые светлые полосы чередуются с темными полосами, • центральный светлый максимум в два раза шире вторичных максимумов. 29
Дифракционные картины Распределение интенсивности sin темн = 2 / a sin темн = / a sin темн = - / a sin темн = -2 / a Экран Характерные черты дифракционной картины: • широкая центральная светлая полоса, • намного более слабые светлые полосы чередуются с темными полосами, • центральный светлый максимум в два раза шире вторичных максимумов. 29
 Контрольный вопрос a Если уменьшить ширину щели на рисунке вдвое, то ширина центрального максимума (a) увеличится, (б) останется неизменной, (в) уменьшится. 30
Контрольный вопрос a Если уменьшить ширину щели на рисунке вдвое, то ширина центрального максимума (a) увеличится, (б) останется неизменной, (в) уменьшится. 30

