Внетабличное умножение и деление Содержание темы Изучение

Внетабличное умножение и деление Содержание темы: • Изучение свойств умножения и деления; • умножение и деление чисел оканчивающихся нулями; • умножение и деление двузначного числа на однозначное; • деление двузначного числа на двузначное; • Деление с остатком

Цели и задачи изучения темы - Изучить приемы вычислений для случаев: ав х с, ав : с, а х вс, ав : сд. и сформировать соответствующие вычислительные навыки - Разъяснить свойства арифметических действий как основу формирования вычислительных навыков ( а + в) х с; (а + в) : с; а х в = в х а. - Сформировать умение выполнять деление с остатком.

Внетабличное умножение и деление 24 х 3 = (20 + 4) х 3 = 20 х 3 + 4 х 3 = 60 + 12 = 72 (1) (3) (4) (5) (2) Учащиеся должны: - уметь представлять число в виде суммы разрядных слагаемых -Знать правило умножения суммы на число - (2) -уметь находить произведение вида: 40 х 2 = 80 - (3) 4 дес. Х 2 = 8 дес - знать табличное умножение - (4) - Уметь выполнять сложение в пределах ста - (5) - (1)

Умножение суммы на число (a + b) x c = (a + b) +…. . + (a + b) C раз

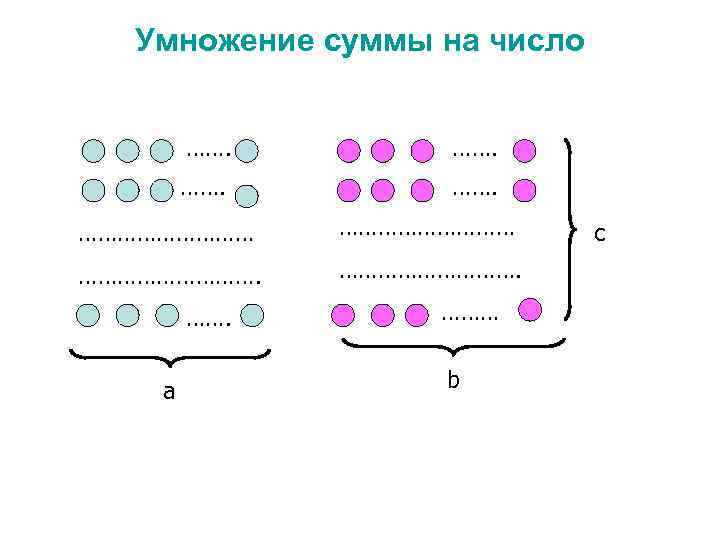
Умножение суммы на число ……. ………………………. ……. a ……… b с

Правило умножения суммы на число • Посчитай сколько здесь всех фигур. Как можно это сделать? 1) (2 + 3) х 4 = 5 х 4 = 20 (2 + 3) х 4 = 2 х 4 + 3 х 4 2) 2 х 4 + 3 х 4 = 8 + 12 = 20

СВОЙСТВА УМНОЖЕНИЯ

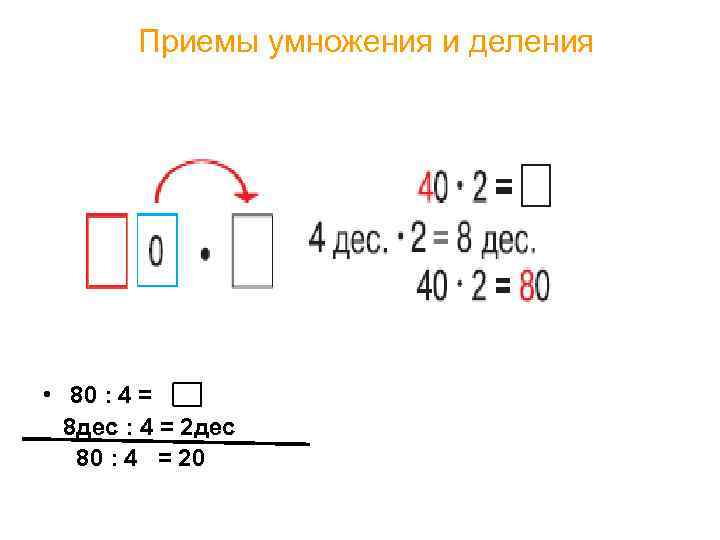
Приемы умножения и деления • 80 : 4 = 8 дес : 4 = 2 дес 80 : 4 = 20

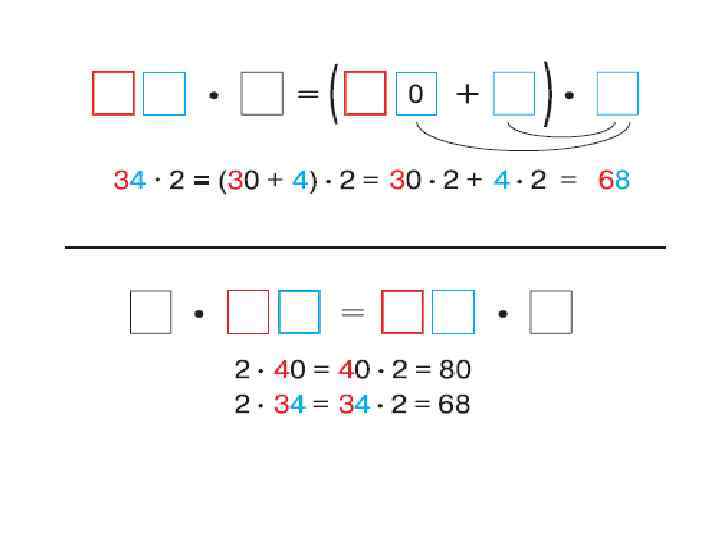
Внетабличное деление • Деление двузначного числа на однозначное 1) 64 : 2 делимое заменяем суммой разрядных слагаемых 2) 70 : 2 делимое заменяют суммой удобных слагаемых 3) 72 : 6 делимое заменяют суммой слагаемых одно из которых двузначное разрядное другое не разрядное

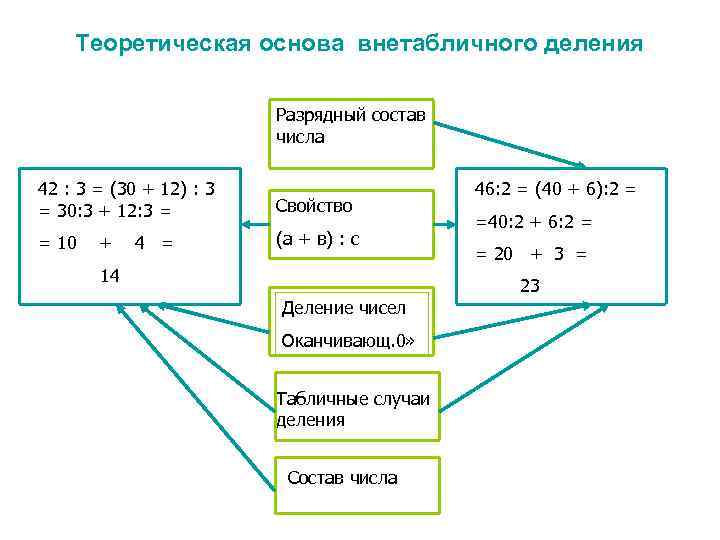
Теоретическая основа внетабличного деления Разрядный состав числа 42 : 3 = (30 + 12) : 3 = 30: 3 + 12: 3 = Свойство = 10 (а + в) : с + 4 = 14 46: 2 = (40 + 6): 2 = =40: 2 + 6: 2 = = 20 + 3 = 23 Деление чисел Оканчивающ. 0» Табличные случаи деления Состав числа

Алгоритм деления • 42 : 3 = (30 + 12) : 3 = 30 : 3 + 12 : 3 = 10 + 4 = 14 1. Представим делимое в виде суммы удобных слагаемых, для этого: - выделим самое большое число десятков. Которое делится на делитель ( 3 д. или 30) ; - вычтем из делимого выделенное число десятков- это второе слагаемое (42 – 30 = 12); 2. Получившуюся сумму разделим на делитель ( (30+12): 2). 3. Воспользуемся правилом деления суммы на число: ( 30 : 3 + 12 : 3 ). 4. Выполним вычисления (10 + 4 = 14).

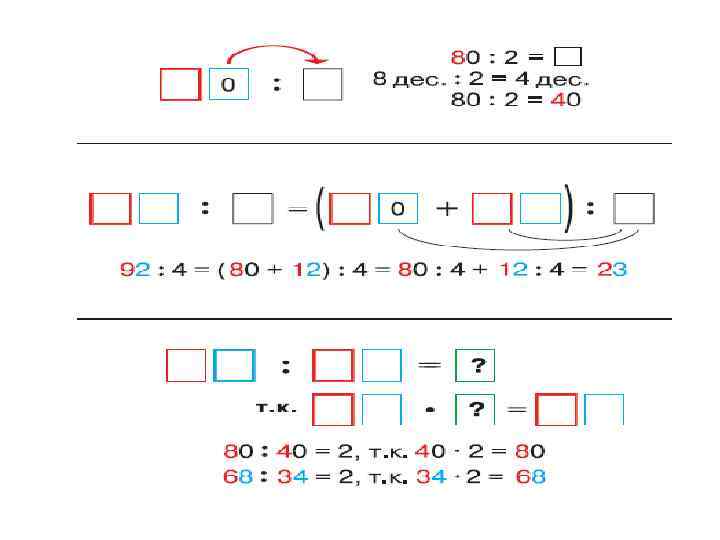
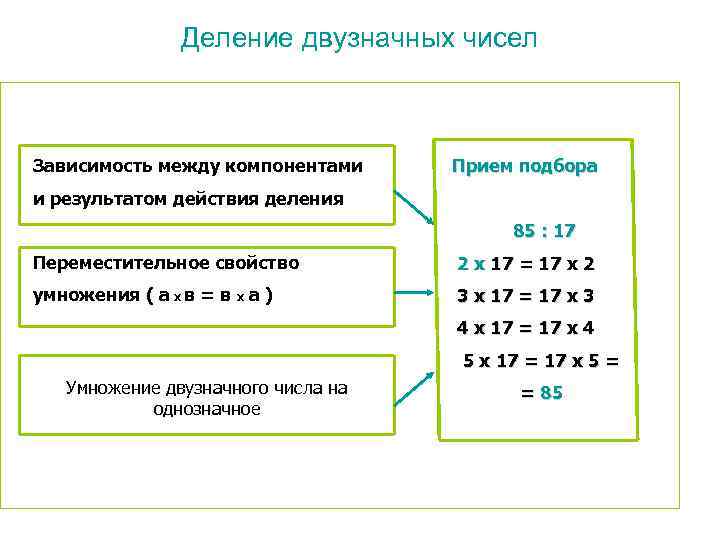
Деление двузначных чисел Зависимость между компонентами Прием подбора и результатом действия деления 85 : 17 Переместительное свойство 2 х 17 = 17 х 2 умножения ( а х в = в х а ) 3 х 17 = 17 х 3 4 х 17 = 17 х 4 5 х 17 = 17 х 5 = Умножение двузначного числа на однозначное = 85

ВЫВОД Разделить одно число на другое , значит найти такое число , которое при умножении на делитель дает делимое Еще раз показали, что умножение и деление взаимосвязаныдва взаимно обратных действия

Деление с остатком Последовательность изучения темы • Раскрывается конкретный смысл деления с остатком; • Устанавливается отношение между остатком и делителем; • Знакомим с приемом деления с остатком; • Составляем алгоритм деления с остатком.

Конкретный смысл деления I. Решаем простые задачи на деление по содержанию и деление на равные части ( практическим способом). Например. Разложите 11 кругов по 2 круга. Узнайте , сколько раз по 2 круга получится? Сколько кругов осталось? 1 2 3 4 5

Продолжение II. Разложи 14 звездочек в 4 конверта поровну. Узнай сколько звездочек в каждом конверте? Сколько звездочек осталось?

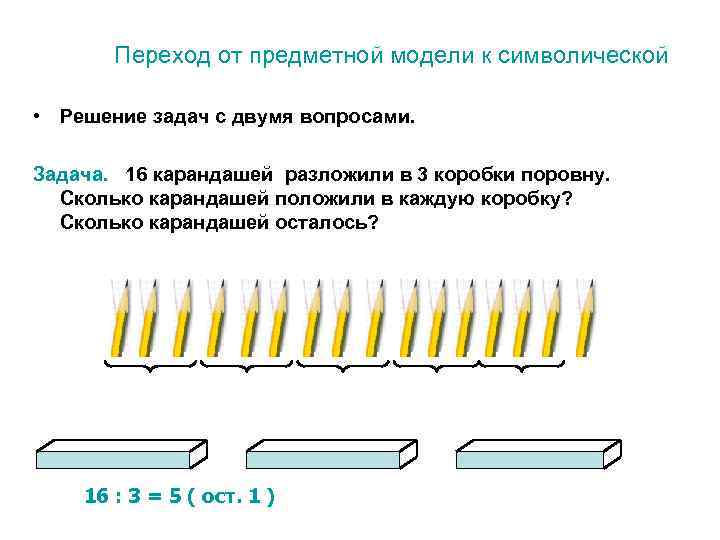
Переход от предметной модели к символической • Решение задач с двумя вопросами. Задача. 16 карандашей разложили в 3 коробки поровну. Сколько карандашей положили в каждую коробку? Сколько карандашей осталось? 16 : 3 = 5 ( ост. 1 )

Раскрываем отношение между делителем и остатком 10 : 2 = 5 12 : 3 = 4 16 : 4 = 4 11 : 2 = 5 (ост 1) 13 : 3 = 4(ост 1) 17 : 4 = 4( ост 1) 12 : 2 = 6 14 : 3 = 4(ост 2) 18 : 4 = 4( ост 2) 13 : 2 = 6 (ост 1) 15 : 3 = 5 19 : 4 = 4 (ост 3) 14 : 2 = 7 16 : 3 = 5 (ост 1) 20 : 4 = 5 15 : 2 = 7 (ост 1) 17 : 3 = 5 (ост 2) 21 : 4 = 5 (ост 1) 16 : 2 = 8 18 : 3 = 6 22 : 4 = 5 (ост 2) 17 : 2 = 8 (ост 1) 19 6 3 = 6 (ост 1) 23 : 4 = 5 (ост 3) ……………. . ……………………… Остаток всегда меньше делителя

Составление алгоритма деления с остатком • Подготовительные упражнения: 1. Назови числа от 6 до 60, которые делятся на 6, 7, 8 , 9. 2. Выдели из числа 47 ( 52, 61, 38) самое большое число, которое делится на 8, 9, 6, 5. 3. Выполни деление. 20 : 4 = 48 : 8= 21 : 4 = 49 : 8 = 54 : 9 = 60 : 9 = 4. Вычисли ( подробное комментирование) 37 : 8

Подробный комментарий 47 : 5 = (ост ) - Это деление с остатком, значит, надо найти два числа – частное и остаток. - Чтобы найти частное из числа 47 выделим самое большое число, которое делится на 5 это – 45. 45 : 5 = 9 9 – это частное, - Чтобы найти остаток вычтем из 47 – 45 = 2 2 – это остаток. 47 : 5 = 9 (ост 2).

Типичные ошибки и их предупреждение • 47 : 5 = 8 (ост 7) • Может ли при делении на 6 в остатке получиться 8? • Назови остатки, которые могут получиться при делении на 11 • Сколько различных остатков получается при делении? на 23 ( 19, 47, 52 ) Найди ошибки

Особые случаи умножения и деления

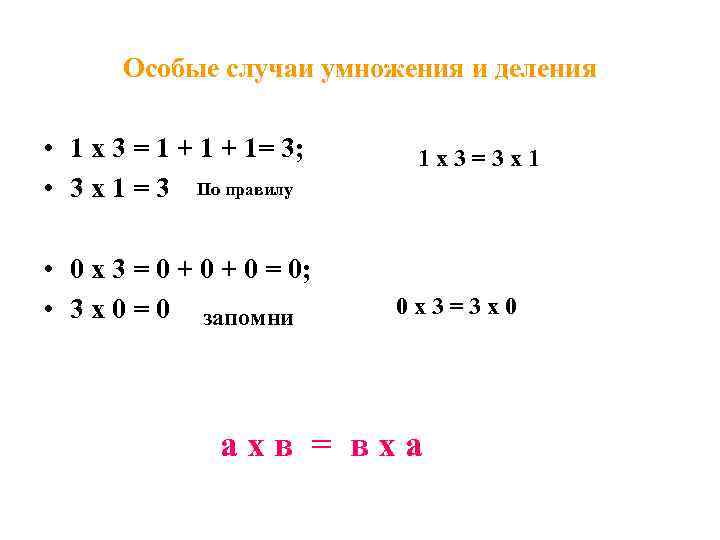
Особые случаи умножения и деления • 1 х 3 = 1 + 1= 3; • 3 х 1 = 3 По правилу • 0 х 3 = 0 + 0 = 0; • 3 х 0 = 0 запомни 1 х3=3 х1 0 х3=3 х0 ахв = вха