viscous gas flow in thin layers with fixed

viscous gas flow in thin layers with fixed boundaries

The object of this study is the gas flow in a thin, straight cracks. Purpose - to create a method and algorithm for calculating the characteristics of the flow of a viscous gas in a thin layer. Outline a new method of calculation that takes into account the small thickness of the slits and the viscosity of gas, based on the assumption of constant pressure and the width of the micro cracks.

well-known scholars of my field of scientific knowledge Daniel Bernoulli Gabriel Stokes (1700 -1782) (1819 -1903) Jean Louis Marie Poiseuille (1797 -1869) Osborne Reynolds (1842 -1912)

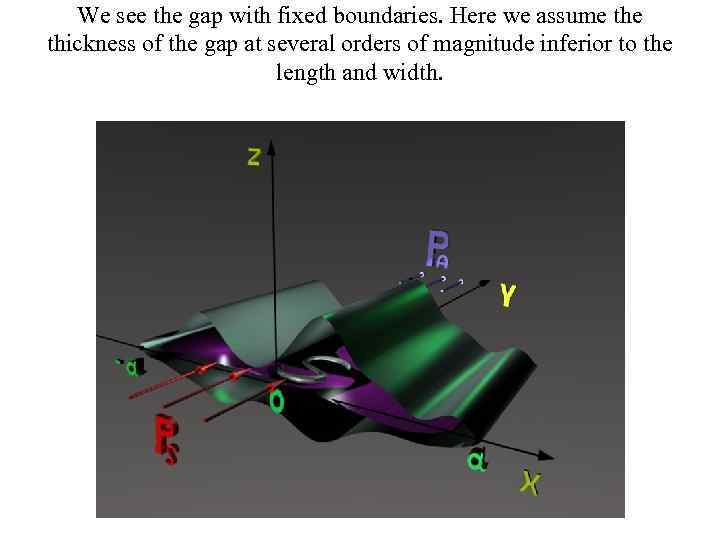We see the gap with fixed boundaries. Here we assume thickness of the gap at several orders of magnitude inferior to the length and width.

navier – stokes continuity equation energy balance equation of state

equations expressing the generalized newton's law of viscous stress tensor due to the tensor of deformation rates expression for determining the mass flow expression to determine the speed of sound in gas sutherland's formula for the dynamic viscosity

To study the flow of the gas we use equations but this system is not only difficult to solve, but also setting the boundary conditions for it are difficult. To overcome this problem, perform the simplification of the system. The gas flow take steady, laminar and isothermal, the equations presented in neglect quantities of order in comparison with unity and forces of inertia of the gas flow, and we assume that: After simplifying the system of equations reduces to

Pressure field in the micro cracks can be determined by solving the Reynolds equation, which in Cartesian coordinate system with the view of the accepted conditions of the form: Take the pressure does not depend on the transverse coordinateand obtain the solution expression to determine the velocity has the form

Applying the ideal gas equation, we obtain We compute also the force of friction that occurs during gas flow through the gap. Assuming a flat bottom surface, are able to find the field of viscous stresses on the surface (known normal at any point)

The remaining components of the viscous stress tensor vanish Total force of friction on the upper boundary is defined as follows: calculate the total force of friction, given that it is balanced by a pressure drop of gas As a result of numerical experiments it was found the general equality of frictional forces on the upper and lower limits for cracks of various forms of.

results obtained in this research work can be used to improve estimates of leakage of gases through the cracks in the walls of pressure vessels

literature • 1. Snopov A. Theory of working of gas static supports. Rostovon-Don, 2009 • 2. Methodological guidelines for thermal and gas dynamic calculations for testing gas turbine pumping units ПР 5131323949 -43 -99 • 3. Guidelines for the calculation of total emissions of hydrocarbons(total) in the atmosphere. OAO "Gazprom“ 112005 •