ВІЙСЬКОВА АКАДЕМІЯ Кафедра фундаментальних наук Навчальна дисципл і

ВІЙСЬКОВА АКАДЕМІЯ Кафедра фундаментальних наук Навчальна дисципл і на ФІЗИКА : Блок змістових модулів 1 ФІЗИЧНІ ОСНОВИ МЕХАНІКИ Змістовий модуль 1 ОСНОВИ КЛАСИЧНОЇ МЕХАНІКИ Л Е К Ц І Я № 1/4 ТЕМА ЗАНЯТТЯ: Динаміка поступального та обертального руху. НАВЧАЛЬНА МЕТА: 1. Ознайомити курсантів з основними поняттями класичної динаміки 2. Дати курсантам знання про основні динамічні характеристики, закономірності поступального та обертального руху та про їх взаємозв`язок 3. Дати методичні вказівки щодо роботи на самопідготовці (СР- 2). ОСНОВНІ ПИТАННЯ : 1. Характеристики та закони динаміки поступального руху. 2. Характеристики та закони динаміки обертального руху. 3. Закони збереження імпульсу та моменту імпульсу у замкненій системі тіл ЛІТЕРАТУРА, РЕКОМЕНДОВАНА ДЛЯ САМОПІДГОТОВКИ 1. Шлапак В. О. Фізика. ч. І. МЕХАНІКА ОІСВ. 1999. , с. 30 -74. 2. Дроздов М. А. , Мартыщенко О. И. , Дзенеладзе Г. И. , ФИЗИКА. ч. І, ОВВОКИУ ПВО, 1986, с. 33 -65 12/15/

ПИТАННЯ 1 ХАРАКТЕРИСТИКИ ТА ЗАКОНИ ДИНАМІКИ ПОСТУПАЛЬНОГО РУХУ

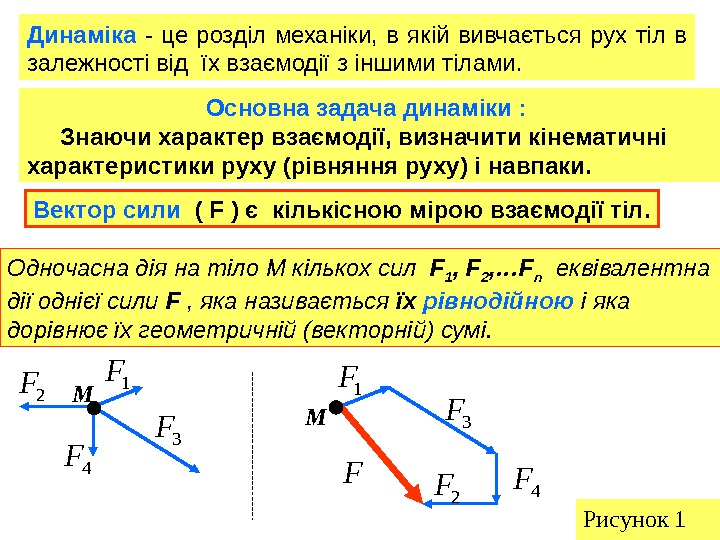
Динаміка — це розділ механіки, в якій вивчається рух тіл в залежності від їх взаємодії з іншими тілами. Основна задача динаміки : Знаючи характер взаємодії, визначити кінематичні характеристики руху (рівняння руху) і навпаки. Вектор сили ( F ) є кількісною мірою взаємодії тіл. Одночасна дія на тіло М кількох сил F 1 , F 2 , …F n еквівалентна дії однієї сили F , яка називається їх рівнодійною і яка дорівнює їх геометричній (векторній) сумі. Рисунок 1 М F 1 F 2 F 3 F 4 F М

Закони Ньютона Перший закон Ньютона (закон інерції ): Будь яке тіло зберігає стан відносного спокою або рівномірного прямолінійного руху доти інші тіла своєю дією не змінять цей стан Система відліку, в якій виконується перший закон Ньютона, називається інерціальною Маса тіла ( m ) є кількісною мірою інерції тіла (скалярна величина) В СІ одиницею вимірювання маси є кілограм ( кг ): [ m ] = 1 кг (встановлюється еталоном і є, таким чином, основною одиницею системи СІ) Крім того, маса m є також мірою здатності тіл до гравітаційної взаємодії

в) маса замкненої системи залишається сталою при будь-яких процесах, які відбуваються в цій системі (закон збереження маси). Вектор імпульсу тіла (р) – це кількісна міра механічного руху будь якого тіла в даному напрямку Імпульс тіла — це вектор р який збігається з напрямком вектора швидкості тіла v і дорівнює добутку його маси на швидкість m (1) Рисунок 10 В класичній механіці вважається , що: а) маса тіла не залежить від стану його руху і є його незмінною характеристикою; б) маса-величина адитивна , тобто маса системи тіл дорівнює сумі мас всіх тіл, які складають цю систему; p v v mp

В системі СІ імпульс тіла вимірюється : [ р ] = 1 кг м/с Імпульсом системи матеріальних точок називається вектор p , який дорівнює векторній сумі імпульсів всіх матеріальних точок p i системи N i ii N i impp 11 v (2) m 3 0 m 1 m 2 m N Прискорення , що будь яке тіло набуває внаслідок взаємодії з іншими тілами, є прямо пропорційним до сили взаємодії і обернено пропорційним до маси даного тіла. m m F a (3) Рисунок 2 Рисунок 3 p p 2 p 1 p 3 p 4 p F a Другий закон Ньютона (основний закон динаміки): Вектор прискорення має такий саме напрямок, як і сила, яка його викликала.

(5) (4) m F dt d a v dt. Fmdpd v Імпульсом сили називається вектор, який дорівнює добутку сили на час її дії Сила дорівнює швидкості зміни імпульсу тіла dt pd F (6) За одиницю сили в СІ взято силу, яка тілу масою 1 кг надає прискорення 1 м/с 2 . [ F ] = 1 кг м / с 2 = 1 Н (ньютон) m i m k Рисунок 4 Третій закон Ньютона ( законі дії та протидії ): Два тіла діють одне на одне з силами рівними за модулем і протилежними за напрямком ikki. FF ki. F ik.

Сили в механіці 1. Сили тяжіння або гравітаційні сили 2 21 r mm GF (7) gm. F (8) : Визначаються законом Гука: (9) де k — коефіцієнт пружності ( жорсткість тіла ), x — зміщення від положення рівноваги. 3. Сили тертя F тер = F N (10) де — коефіцієнт тертя, F N — сила нормального тиску. Визначаються законом Ньютона всесвітнього тяжіння : 2 r m GgÇ Універсальна гравітаційна стала 2. Сили пружності G = 6, 67· 10 − 11 Н·м²·кг − 2 , визначаються формулою : x. Fïð k (11)

ПИТАННЯ 2 ХАРАКТЕРИСТИКИ ТА ЗАКОНИ ДИНАМІКИ ОБЕРТАЛЬНОГО РУХУ

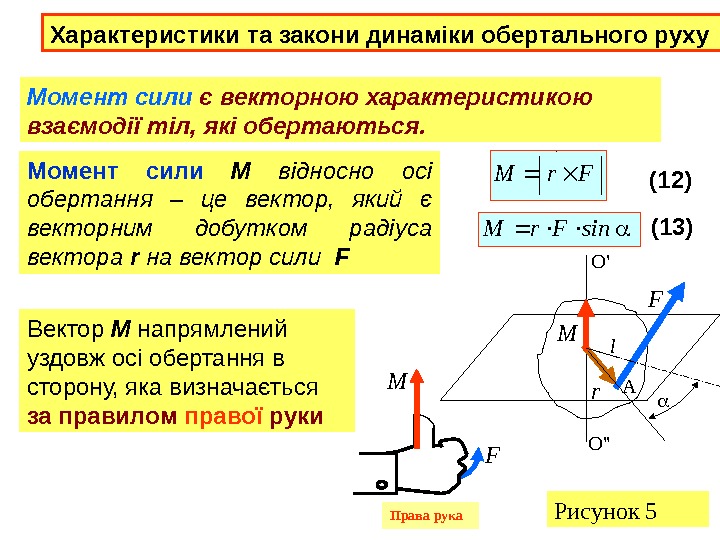
Характеристики та закони динаміки обертального руху Момент сили М відносно осі обертання – це вектор, який є векторним добутком радіуса вектора r на вектор сили FМомент сили є векторною характеристикою взаємодії тіл, які обертаються. Вектор М напрямлений уздовж осі обертання в сторону, яка визначається за правилом правої руки (12) l Рисунок 5 А O » O ‘ Права рука F r. MM r F M F sin. Fr. M (13)

Момент інерції є мірою інерції тіла при обертальному русі. Момент інерції ( I ) є величиною скалярною і для матеріальної точки дорівнює добутку маси на квадрат найменшої відстані цієї точки до осі обертання I i = m i r i 2 O« m i r i (14) В системі СІ момент інерції вимірюється : [ І ] = 1 кг м 2 Момент інерції твердого тіла , яке складається з множини матеріальних точок, відносно даної осі обертання дорівнює сумі моментів інерції всіх таких точок відносно той же осі : I = I i = m i r i 2 , (15) або m dmr. I 0 2 (16) Рисунок

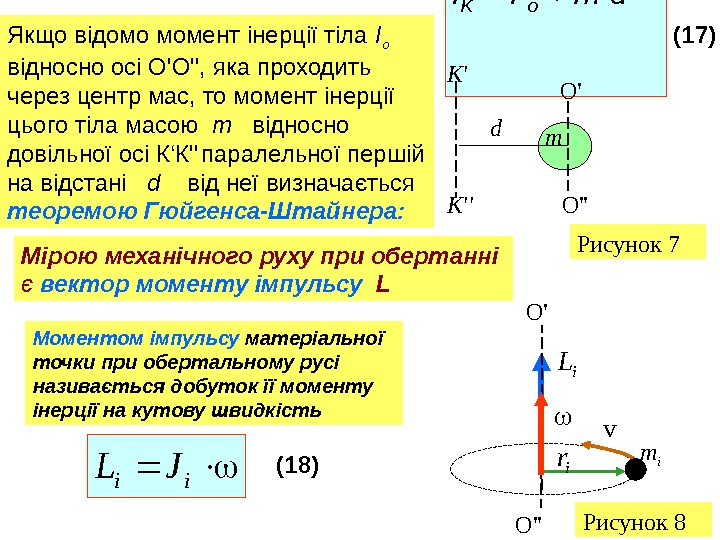
(17) : Якщо відомо момент інерції тіла I o відносно осі O » , яка проходить через центр мас, то момент інерції цього тіла масою m відносно довільної осі К ‘ К » паралельної першій на відстані d від неї визначається теоремою Гюйгенса-Штайнера: I K = I o + m d 2 К » O »O ‘ К ‘ d m Рисунок 7 Мірою механічного руху при обертанні є вектор моменту імпульсу L Моментом імпульсу матеріальної точки при обертальному русі називається добуток її моменту інерції на кутову швидкість (18) O ‘ m i O » Рисунок 8 ii. JL i. L v ir

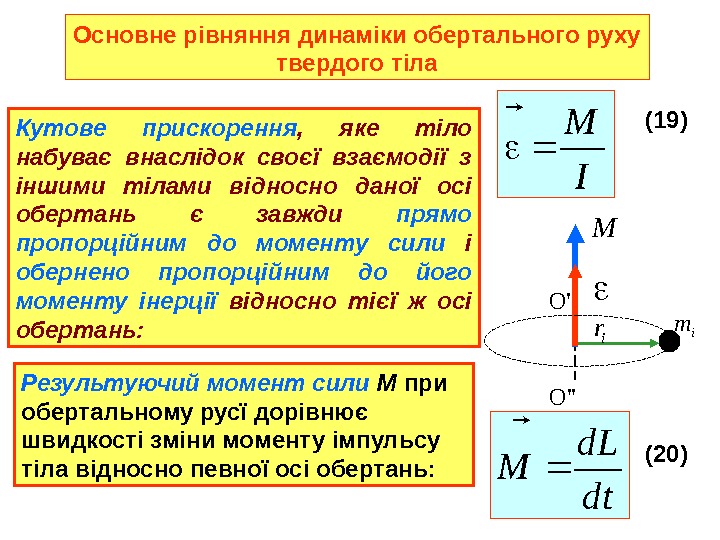
Основ не рівняння динаміки обертального руху твердого тіла Кутове прискорення , яке тіло набуває внаслідок своєї взаємодії з іншими тілами відносно даної осі обертань є завжди прямо пропорційним до моменту сили і обернено пропорційним до його моменту інерції відносно тієї ж осі обертань: I M (19) Результуючий момент сили M при обертальному русї дорівнює швидкості зміни моменту імпульсу тіла відносно певної осі обертань: O ‘ m i O » (20) M ir dt Ld M

ПИТАННЯ 3 ЗАКОНИ ЗБЕРЕЖЕННЯ ІМПУЛЬСУ ТА МОМЕНТУ ІМПУЛЬСУ У ЗАМКНЕНІЙ СИСТЕМІ ТІЛ

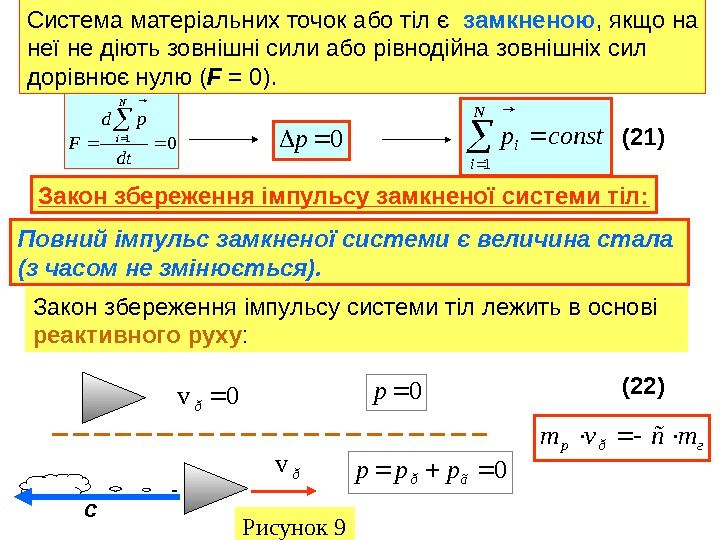
Система матеріальних точок або тіл є замкненою , якщо на неї не діють зовнішні сили або рівнодійна зовнішніх сил дорівнює нулю ( F = 0). 01 dt pd F N i iconstp 1 (21) Повний імпульс замкненої системи є величина стала (з часом не змінюється). Закон збереження імпульсу замкненої системи тіл: Закон збереження імпульсу системи тіл лежить в основі реактивного руху : Рисунок 9 c (22) 0 p 0 vð 0 p ðv 0ãðppp гmñvmðp

Основне рівняння руху тіла змінної маси (рівняння Мещерського)Висновок: реактивний рух тіла спричиняється зміною маси тіла dt dm ñFð (23) де m — маса тіла в даний момент часу , F р — реактивна сила , с — швидкість викидання частинок газу відносно самої ракети, яку називають відносною швидкістю. Формула Ціолковського для визначення кінцевої швидкості ракети v = c ln (1 + m п / m p ) де m p — маса ракети в момент визначення її швидкості, m п — маса палива (24)

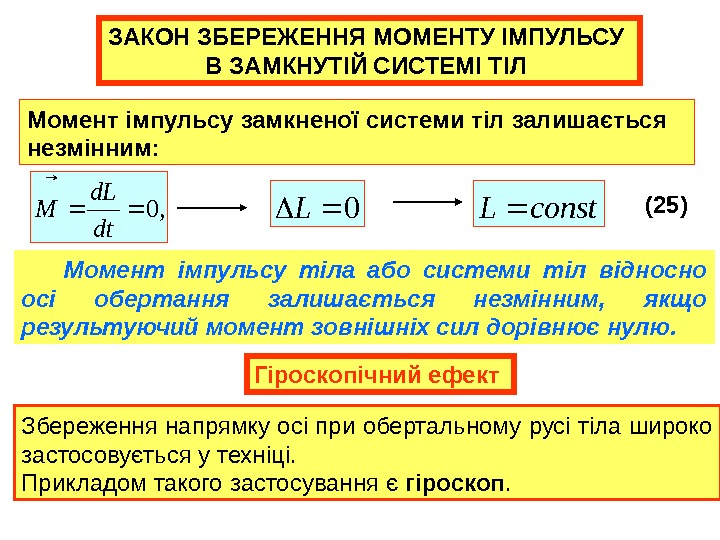
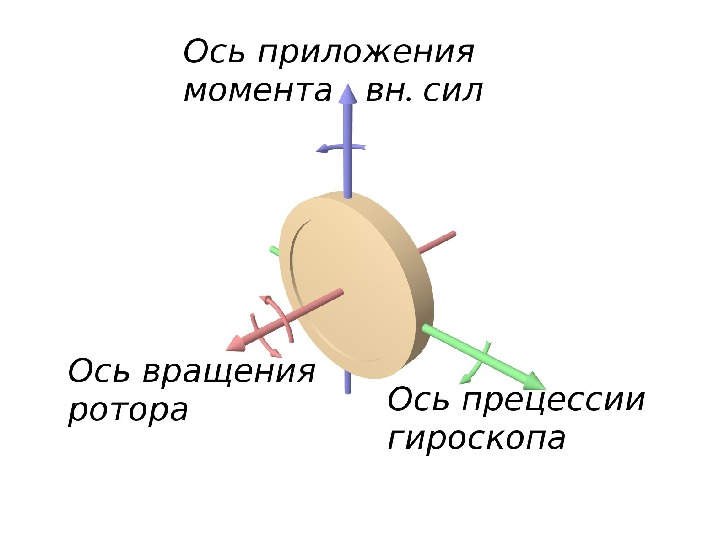
ЗАКОН ЗБЕРЕЖЕННЯ МОМЕНТУ ІМПУЛЬСУ В ЗАМКНУТІЙ СИСТЕМІ ТІЛ Момент імпульсу замкненої системи тіл залишається незмінним: , dt Ld M 0 0 L const. L (25) Момент імпульсу тіла або системи тіл відносно осі обертання залишається незмінним, якщо результуючий момент зовнішніх сил дорівнює нулю. Збереження напрямку осі при обертальному русі тіла широко застосовується у техніці. Прикладом такого застосування є гіроскоп. Гіроскопічний ефект

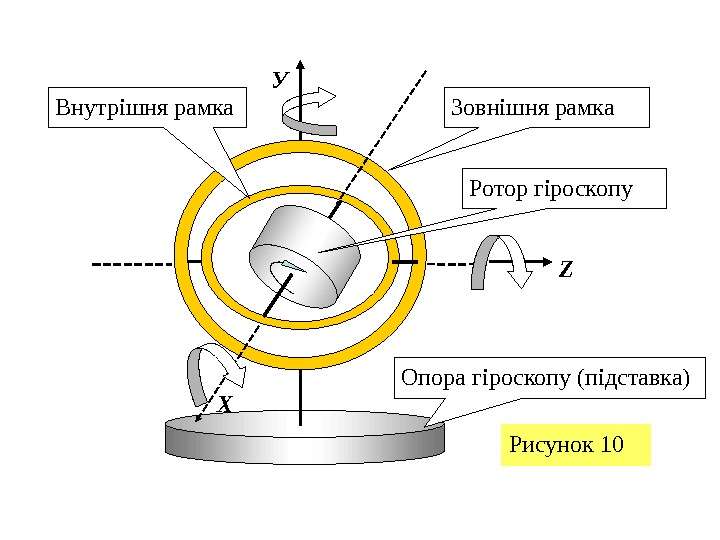
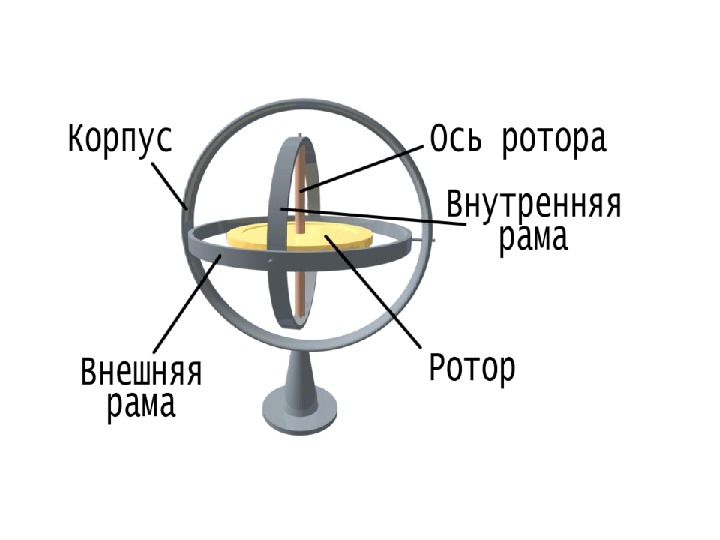
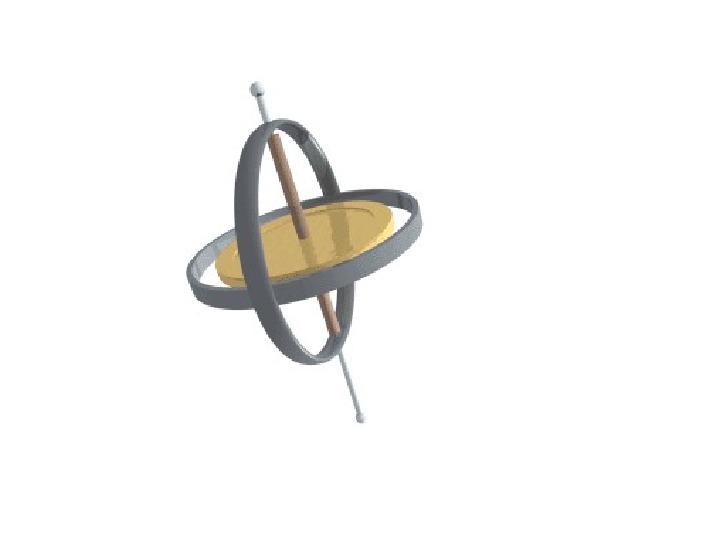
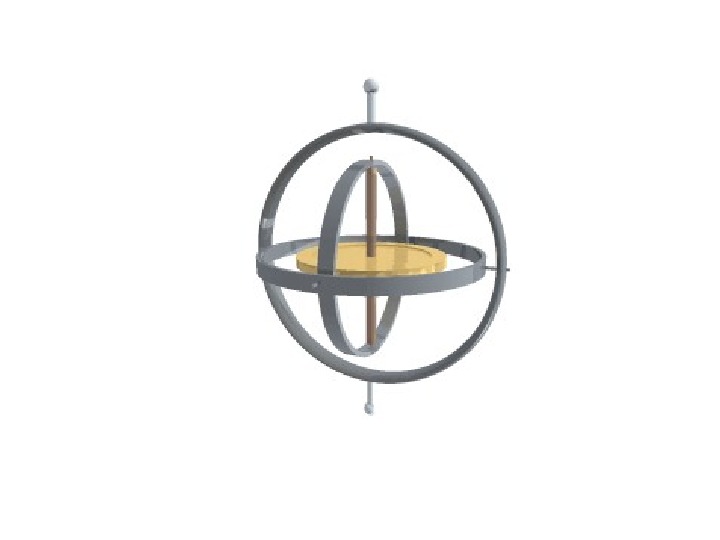
У Z Х Рисунок 10 Опора гіроскопу (підставка)Зовнішня рамка. Внутрішня рамка Ротор гіроскопу

Висновки за темою заняття 1. МИ РОЗГЛЯНУЛИ ХАРАКТЕРИСТИКИ ТА ЗАКОНИ ДИНАМІКИ ПОСТУПАЛЬНОГО РУХУ 2. ВИЗНАЧЕНІ ТАКОЖ ХАРАКТЕРИСТИКИ ТА ЗАКОНИ ДИНАМІКИ ОБЕРТАЛЬНОГО РУХУ 3. БУЛИ ВИЗНАЧЕНІ ФУНДАМЕНТАЛЬНІ ПОНЯТТЯ ТА ЗАКОНОМІРНОСТІ ЗБЕРЕЖЕННЯ ІМПУЛЬСУ ТА МОМЕНТУ ІМПУЛЬСУ У ЗАМКНЕНІЙ СИСТЕМІ ТІЛ 4. БУЛИ НАВЕДЕНІ ПРИКЛАДИ ВИДАТНИХ ЗАСТОСУВАНЬ ДИНАМІКИ В НАУЦІ І ТЕХНІЦІ 1. ПРОРОБИТИ КОНСПЕКТ ЛЕКЦІЇ З ВИКОРИСТАННЯМ РОЗДАТКОВОГО МАТЕРІАЛУ. 2. ВИЗНАЧИТИ ПИТАННЯ, ЯКІ ЗАЛИШАЮТЬСЯ НЕЗРОЗУМІЛИМИ І ЗВЕРНУТИСЯ ДО ТОВАРИШІВ АБО ДО ВИКЛАДАЧА ЗА КОНСУЛЬТАЦІЄЮ. 3. ПІДГОТУВАТИСЯ ДО НАСТУПНИХ ЗАНЯТЬ ШЛЯХОМ ПОВТОРЕННЯ ЛЕКЦІЙНОГО МАТЕРІАЛУ Методичні вказівки на самопідготовку