Viewing in 3 D Chapter 6 — Viewing

Viewing in 3 D Chapter 6 -- Viewing in 3 D

u The 3 D viewing process is inherently more complex than is the 2 D viewing process. F In 2 D, we simply specify a window on the 2 D world and a viewport on the 2 D view surface. F Conceptually, objects in the world are clipped against the window and then transformed into the viewport for display. F Although 3 D viewing may seem overwhelming at first, it is less daunting when viewed as a series of easily understood steps, many of which we have prepared for in earlier chapters. Chapter 6 -- Viewing in 3 D 2

1. The Synthetic Camera and Steps in 3 D Viewing n A useful metaphor for creating 3 D scenes is the notion of a synthetic camera Chapter 6 -- Viewing in 3 D 3

u While the synthetic camera is a useful concept, there is a bit more to producing an image than just pushing a button. u Creation of our photo is accomplished as a series of steps: F Specification of projection type F Specification of viewing parameters F Clipping in three dimensions F Projection and Display Chapter 6 -- Viewing in 3 D 4

2. Projections n In general, projections transform points in a coordinate system of dimension n into points in a coordinate system of dimension less than n. n For now we shall limit ourselves to 3 D to 2 D. Chapter 6 -- Viewing in 3 D 5

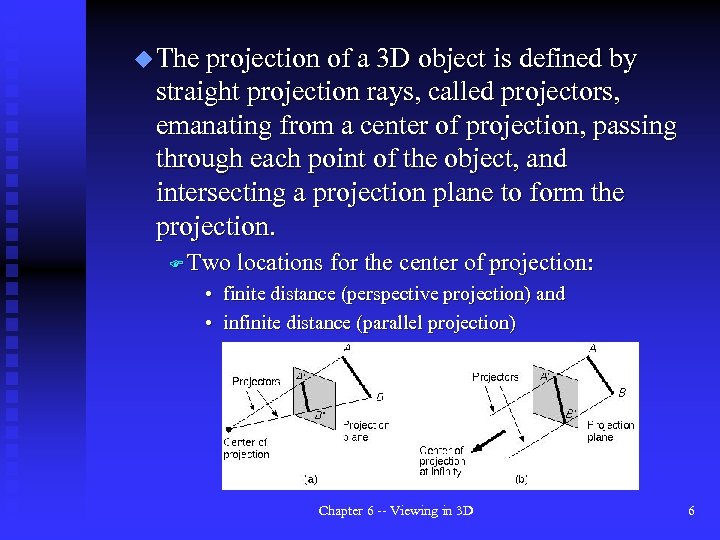u The projection of a 3 D object is defined by straight projection rays, called projectors, emanating from a center of projection, passing through each point of the object, and intersecting a projection plane to form the projection. F Two locations for the center of projection: • finite distance (perspective projection) and • infinite distance (parallel projection) Chapter 6 -- Viewing in 3 D 6

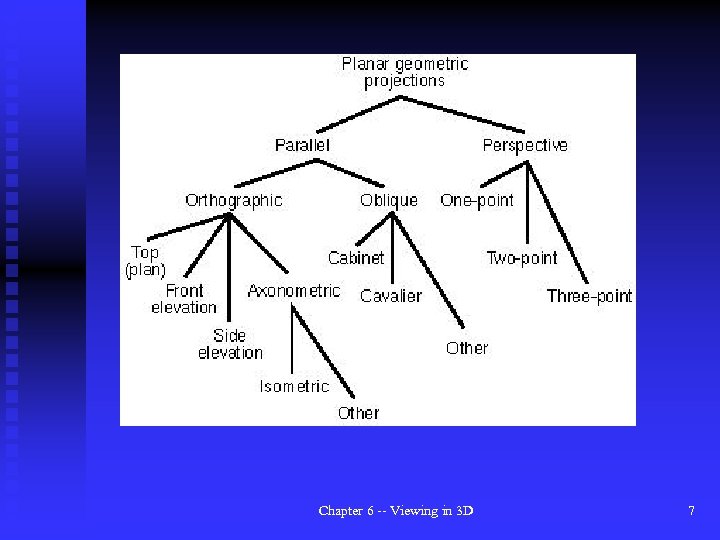Chapter 6 -- Viewing in 3 D 7

2. 1 Perspective Projections u The perspective projections of any set of parallel lines that are not parallel to the projection plane converge to a vanishing point. F if the set of lines is parallel to one of the three principal axes, the vanishing point is called an axes vanishing point Chapter 6 -- Viewing in 3 D 8

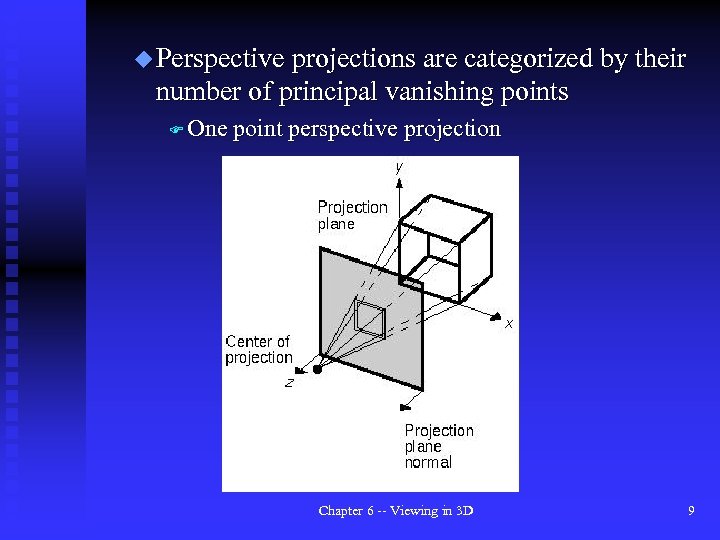u Perspective projections are categorized by their number of principal vanishing points F One point perspective projection Chapter 6 -- Viewing in 3 D 9

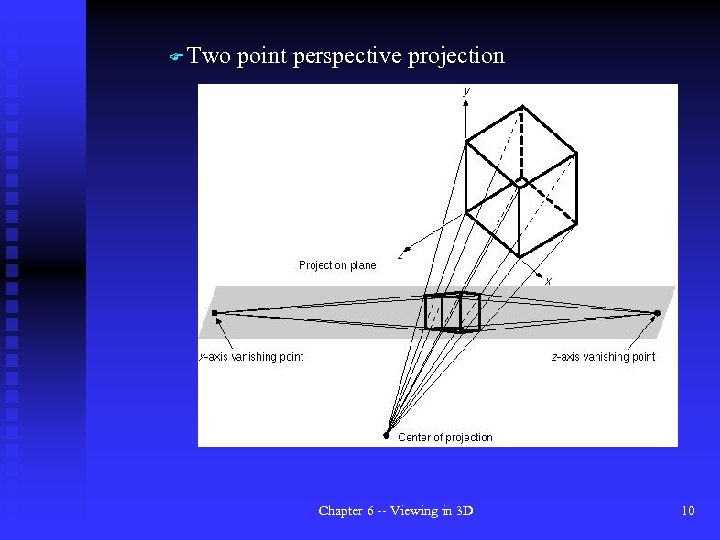F Two point perspective projection Chapter 6 -- Viewing in 3 D 10

2. 2 Parallel Projections u Parallel projections are categorized into two types, depending on the relation between the direction of projection and the normal to the projection plane. u The two most common are: F orthographic -- direction of the projection and the normal of the plane are the same F oblique -- they are not the same. Chapter 6 -- Viewing in 3 D 11

u The most common types of orthographic projections are F front-elevation F top-elevation F side-elevation Chapter 6 -- Viewing in 3 D 12

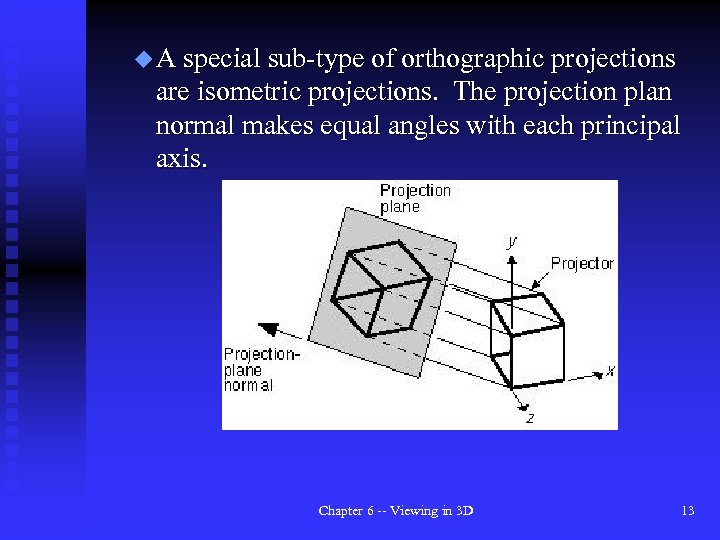u A special sub-type of orthographic projections are isometric projections. The projection plan normal makes equal angles with each principal axis. Chapter 6 -- Viewing in 3 D 13

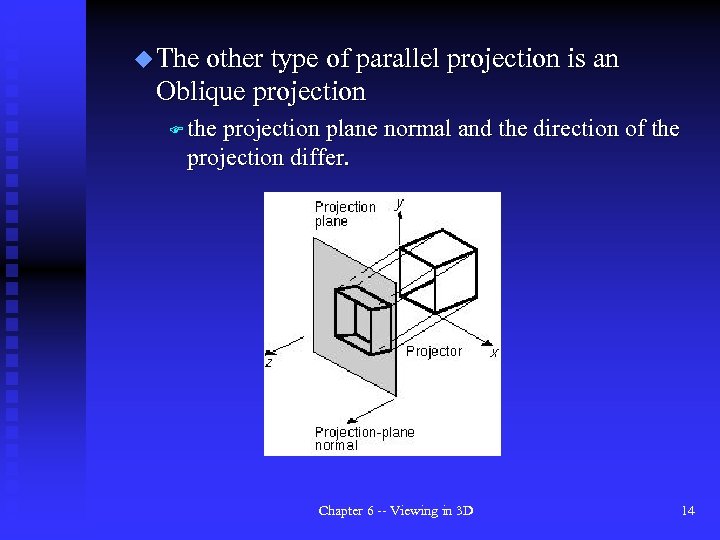u The other type of parallel projection is an Oblique projection F the projection plane normal and the direction of the projection differ. Chapter 6 -- Viewing in 3 D 14

3. Specification of an Arbitrary 3 D View u 3 D viewing involves not just a projection, but also a view volume against which the 3 D world is clipped. u The projection and the view volume together provide all the information that we need to clip and project into 2 D space. u Then the 2 D transformation into physical device coordinates is straightforward. Chapter 6 -- Viewing in 3 D 15

u The projection plane (view plane in the graphics literature) is defined by Fa point in the plane called a view reference point (VRP) and F a normal to the plane called the view-plane normal (VPN) Chapter 6 -- Viewing in 3 D 16

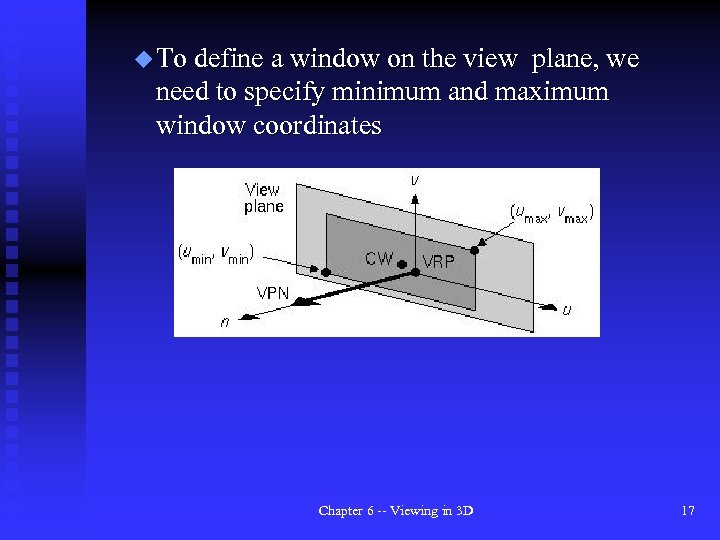u To define a window on the view plane, we need to specify minimum and maximum window coordinates Chapter 6 -- Viewing in 3 D 17

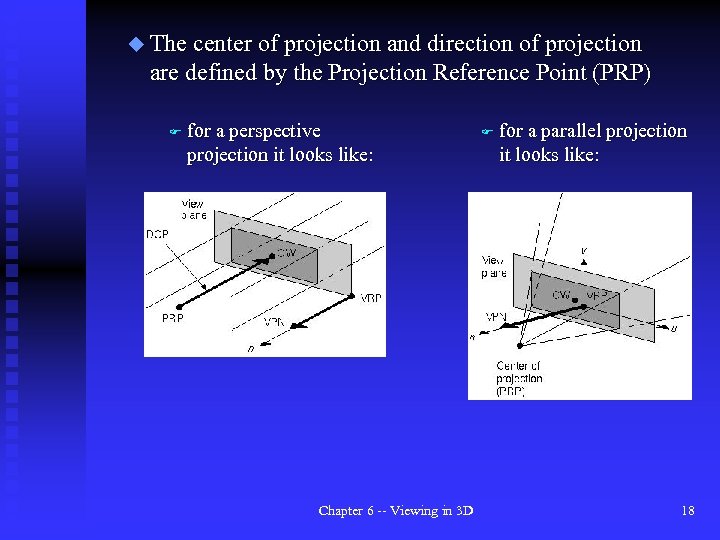u The center of projection and direction of projection are defined by the Projection Reference Point (PRP) F for a perspective projection it looks like: Chapter 6 -- Viewing in 3 D F for a parallel projection it looks like: 18

u At times we may want the view volume to be finite, in order to limit the number of output primitives projected onto the view plane. F You specify the front and back clipping planes F For parallel projections it looks like: F for perspective projections it looks like: Chapter 6 -- Viewing in 3 D 19

4. Examples of 3 D Viewing n In this section, we consider how we can apply the basic viewing concepts introduced in Section 3 to create a variety of projections. u such as this house. Chapter 6 -- Viewing in 3 D 20

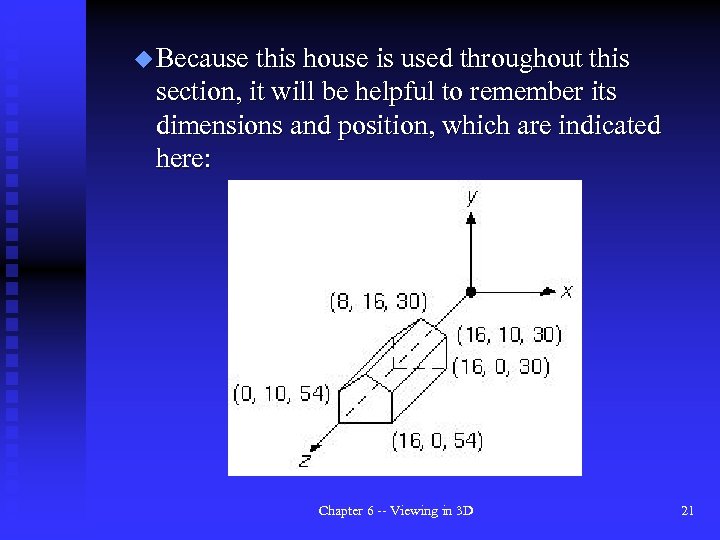u Because this house is used throughout this section, it will be helpful to remember its dimensions and position, which are indicated here: Chapter 6 -- Viewing in 3 D 21

4. 1 Perspective Projections u To obtain the front one-point perspective view shown here: F position the center of projection (the viewer) at (8, 6, 84) Chapter 6 -- Viewing in 3 D 22

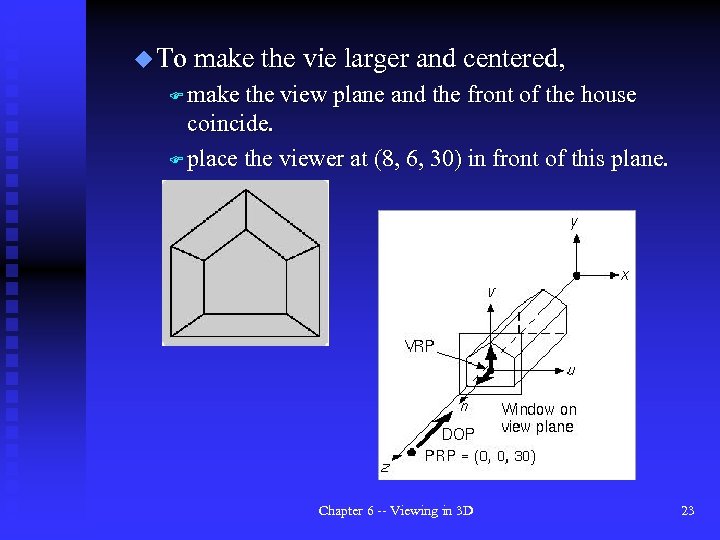u To make the vie larger and centered, F make the view plane and the front of the house coincide. F place the viewer at (8, 6, 30) in front of this plane. Chapter 6 -- Viewing in 3 D 23

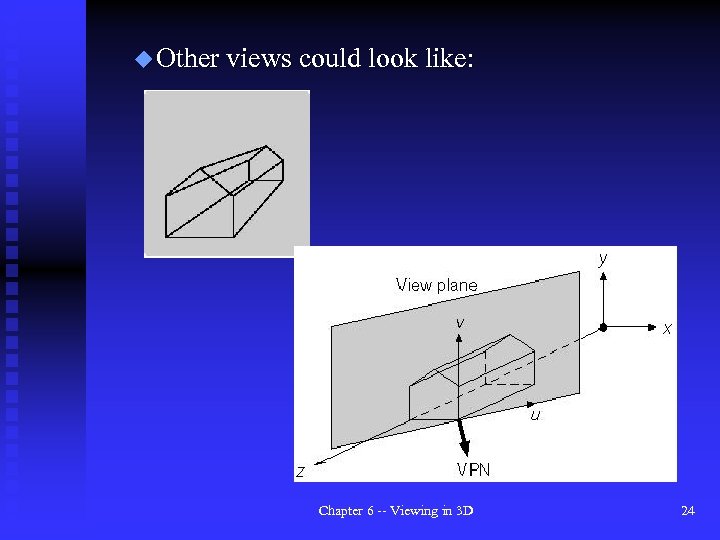u Other views could look like: Chapter 6 -- Viewing in 3 D 24

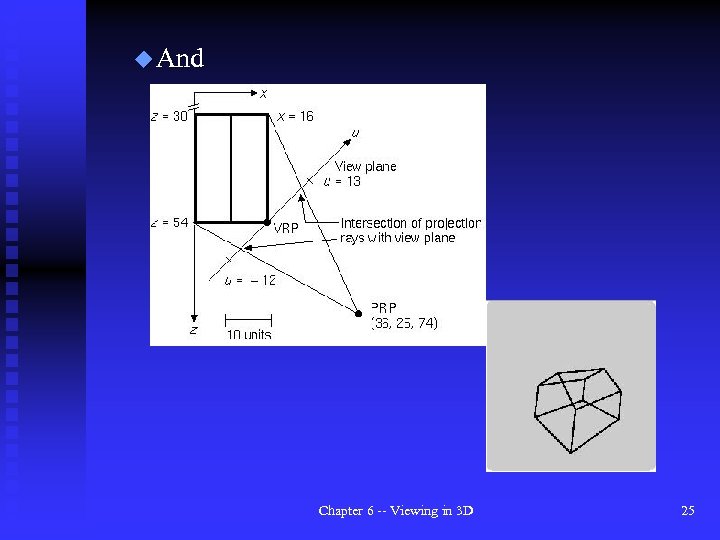u And Chapter 6 -- Viewing in 3 D 25

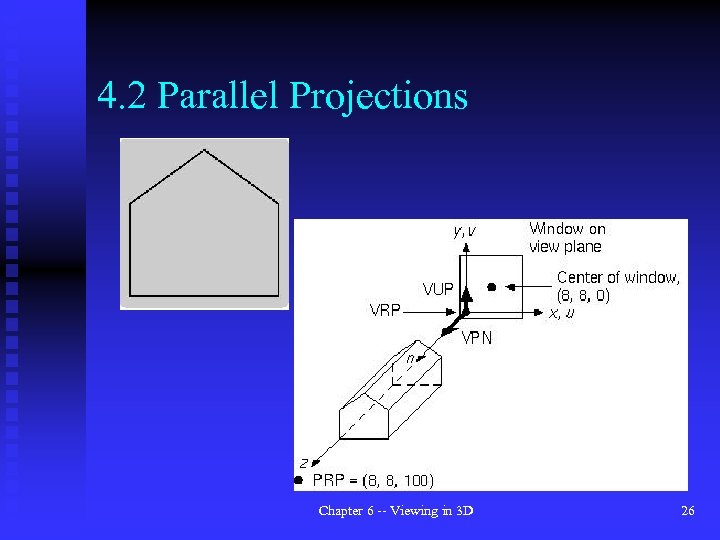4. 2 Parallel Projections Chapter 6 -- Viewing in 3 D 26

4. 3 Finite View Volumes In all the examples so far, the view volume has been assumed to be infinite. n If we start with this setup n Chapter 6 -- Viewing in 3 D 27

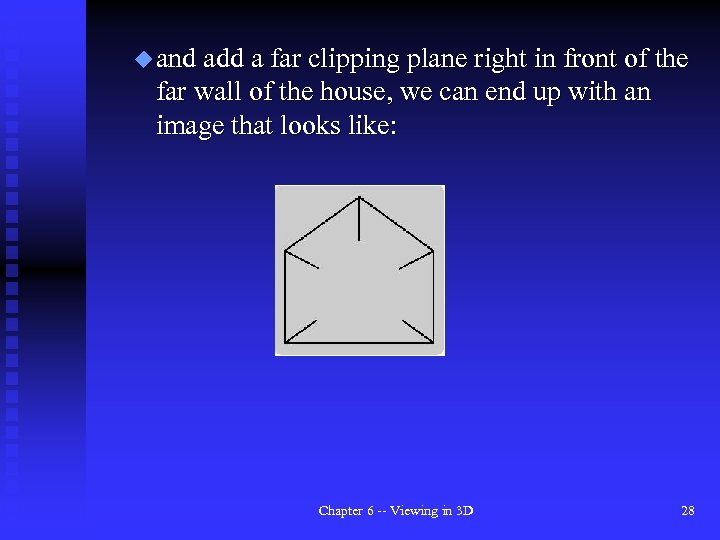u and add a far clipping plane right in front of the far wall of the house, we can end up with an image that looks like: Chapter 6 -- Viewing in 3 D 28

5. The Mathematics of Planar Geometric Projections Here we introduce the basic mathematics of planar geometric projections. n For simplicity, we start by assuming that, n u in the perspective projection, the projection plane is normal to the z axis at z=d, u and that in the parallel projection, the projection plane is at z=0. Chapter 6 -- Viewing in 3 D 29

u Each of the projections can be defined by a 4 x 4 matrix. F This is convenient, because the projection matrix can be composed with the transformation matrices, allowing two operations (transform then project) to be represented in a single matrix. u In this section we derive 4 x 4 matrices for several projections Chapter 6 -- Viewing in 3 D 30

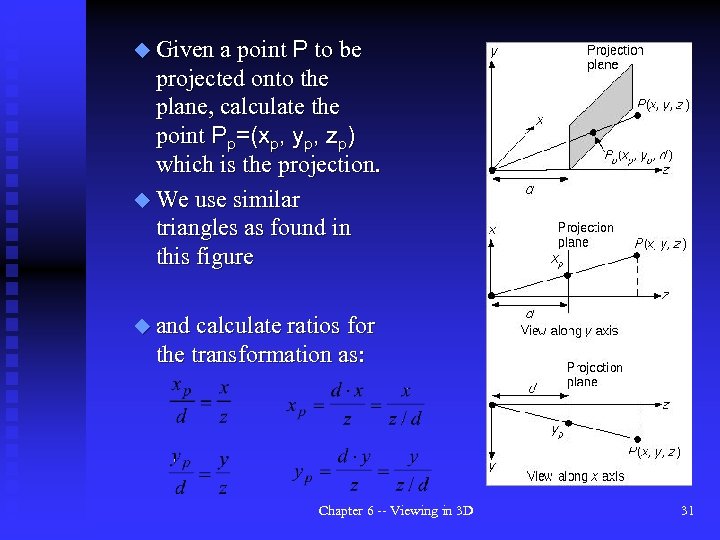u Given a point P to be projected onto the plane, calculate the point Pp=(xp, yp, zp) which is the projection. u We use similar triangles as found in this figure u and calculate ratios for the transformation as: Chapter 6 -- Viewing in 3 D 31

u These ratios lead to a transformation matrix for a perspective projection of: Chapter 6 -- Viewing in 3 D 32

u The orthographic projection pane at z=0 is straightforward, and ends up as: Chapter 6 -- Viewing in 3 D 33

6. Implementation of Planar Geometric Projections Given a view volume and a projection, let us consider how the viewing operation of clipping and projecting is applied. n The brute force method was: n u clip each line with the 6 planes of the volume. u project remaining lines by solving simultaneous equations for the projection onto the view plane u Then transform these to 2 D space. . . Chapter 6 -- Viewing in 3 D 34

u The large number of calculations required for this process, repeated for many lines, involves considerable computing. u Happily there is a more efficient procedure, based on the divide-and-conquer strategy of breaking down a difficult problem into a series of simpler ones. F And they are much easier if you use the canonical volumes shown here: Chapter 6 -- Viewing in 3 D 35

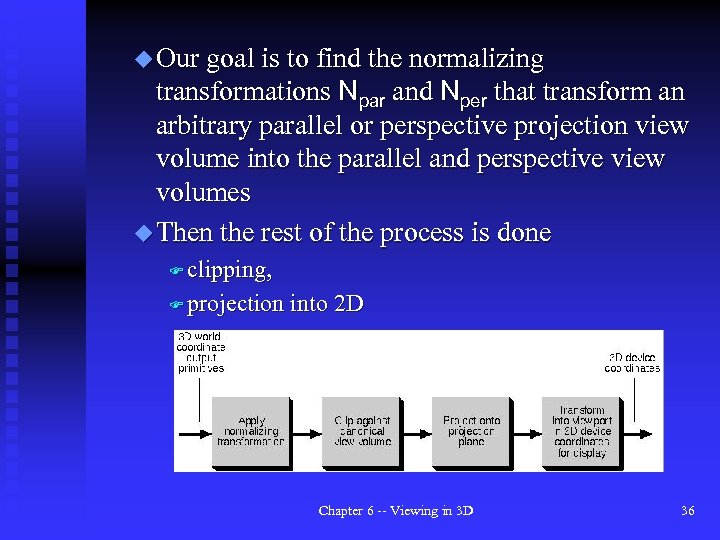u Our goal is to find the normalizing transformations Npar and Nper that transform an arbitrary parallel or perspective projection view volume into the parallel and perspective view volumes u Then the rest of the process is done F clipping, F projection into 2 D Chapter 6 -- Viewing in 3 D 36

6. 1 The Parallel Projection Case In this section, we derive the normalizing transformation Npar for parallel projections. n This is done in order to transform worldcoordinate positions such that the view volume is transformed into the canonical view volume. n Then we clip and project. n Chapter 6 -- Viewing in 3 D 37

u Transformation Npar is derived for the most general case, the oblique (rather than the orthographic) parallel projection. u Npar thus includes a shear transformation that causes the direction of projection in viewing coordinates to be parallel to z. F By including this shear we can do the projection onto z=0 plane simply by setting z=0. Chapter 6 -- Viewing in 3 D 38

u The series of transformations that make up Npar is as follows: F Translate the VRP to the origin F Rotate VRC such that the n axis (VPN) becomes the z axis, the u axis becomes the x axis, and the v axis becomes the y axis. F Shear such that the direction of projection becomes parallel to the z axis. F Translate and scale into the parallel-projection canonical view volume. Chapter 6 -- Viewing in 3 D 39

6. 2 The Perspective Projection Case u We now develop the normalizing transformation Nper for perspective projections. u Nper transforms world-coordinate positions such that the view volume becomes the perspectiveprojection canonical view volume, the truncated pyramid with the apex at the origin. u Then you clip and project using Mper derived in section 6. 5. Chapter 6 -- Viewing in 3 D 40

u The series of transformations making up Nper as follows: F Translate VRP to the origin F Rotate VRC such that the n axis (VPN) becomes the z axis, the u axis becomes the x axis, and the v axis becomes the y axis. F Translate such that the center of projection (COP), given by the PRP, is at the origin. F Shear that the center line of the view volume becomes the z axis F Scale such that the view volume becomes the canonical perspective view volume, the truncated right pyramid. Chapter 6 -- Viewing in 3 D 41

u This figure presents the view volume before and after the steps just described. Chapter 6 -- Viewing in 3 D 42

6. 3 Clipping Against a Canonical View Volume in 3 D u The canonical view volumes are: F the 2 x 2 x 1 prism for parallel projections F the truncated right regular pyramid for perspective projections Chapter 6 -- Viewing in 3 D 43

u Both the Cohen-Sutherland Cyrus-Beck clipping algorithms discussed in Chapter 3 readily extend to 3 D u There also other clipping algorithms that are based on parametric expressions that can be more efficient than the simple Cohen. Sutherland algorithm (see Chapters 6 and 19 of Foley, van. Dam, et. al. --the big white book). Chapter 6 -- Viewing in 3 D 44

6. 4 Clipping in Homogeneous Coordinates u There are two reasons to clip in homogeneous coordinates: F efficiency • translate perspective canonical to parallel canonical and do a single clip -- Hardware does this. F if you get a point with negative W it can be clipped in homogeneous, but not in 3 D • get negative W’s from unusual homogeneous transformations and from the use of parametric splines. Chapter 6 -- Viewing in 3 D 45

u With regard to clipping, it can be shown that the transformation from the perspectiveprojection canonical view volume to the parallel-projection canonical view volume is: Chapter 6 -- Viewing in 3 D 46

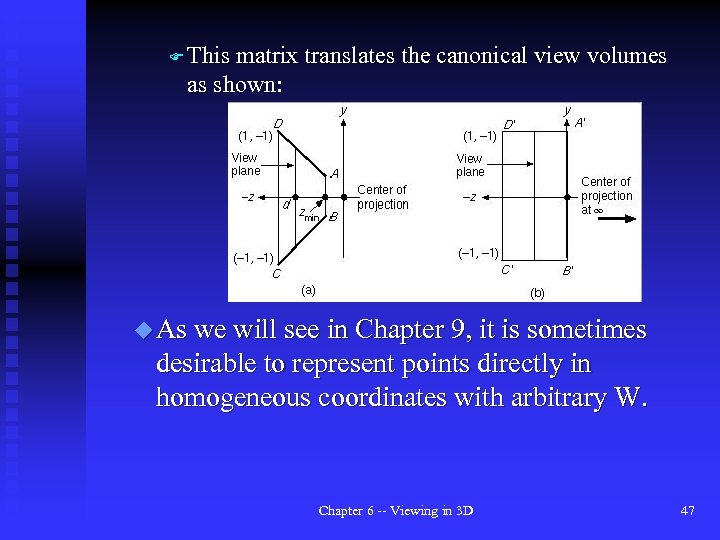F This matrix translates the canonical view volumes as shown: u As we will see in Chapter 9, it is sometimes desirable to represent points directly in homogeneous coordinates with arbitrary W. Chapter 6 -- Viewing in 3 D 47

6. 5 Mapping into a Viewport n Output primitives are clipped in the normalized projection coordinate system, which is also called the 3 D screen coordinate system Chapter 6 -- Viewing in 3 D 48

6. 6 Implementation Summary u There are two generally used implementations of the overall viewing transformation F The first was discussed in Sections 6. 6. 1 through 6. 6. 3 • appropriate when primitives are defined in 3 D and the transformations never create a negative W. F The second was discussed in Section 6. 6. 4 • required whenever primitives are defined and might have W<0, when transformations might create a W<0, or a single clip algorithm is implemented. Chapter 6 -- Viewing in 3 D 49

7. Coordinate Systems u Several different coordinate systems have been used in Chapters 5 and 6. u In this section we summarize all the systems, and also discuss their relationships to one another. Chapter 6 -- Viewing in 3 D 50

u Object Coordinate System F This is the system farthest removed from the actual display device. F The term local coordinate system is also commonly used here u World Coordinate System F Objects are transformed into this system by a modeling transformation. F This system is sometimes called the applicationcoordinate system -- Viewing in 3 D Chapter 6 51

u The View-Reference coordinate system F used by some systems to define a view volume. F sometimes called the eye-coordinate system or the camera-coordinate system. u Normalized-Projection coordinate system F or 3 D screen coordinates. F it is called normalized because the values are in the interval [0, 1] (or [-1, 1]) Chapter 6 -- Viewing in 3 D 52

u The 2 D Device coordinate system F projections from 3 D into 2 D creates this. F also called many other things: screen coordinate system, . . . u Unfortunately there is no single standard usage for many of these terms. F for example, the term screen-coordinate system is used by different authors to refer to the last three systems discussed. Chapter 6 -- Viewing in 3 D 53