Виды сил в Механике Центральная сила

Виды сил в Механике

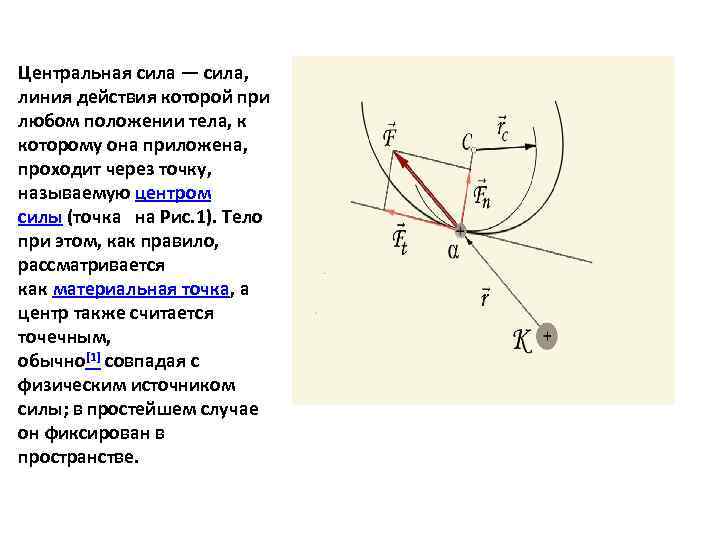Центральная сила — сила, линия действия которой при любом положении тела, к которому она приложена, проходит через точку, называемую центром силы (точка на Рис. 1). Тело при этом, как правило, рассматривается как материальная точка, а центр также считается точечным, обычно[1] совпадая с физическим источником силы; в простейшем случае он фиксирован в пространстве.

• Kлассическая физика вводит также понятие поля центральной силы для области трёхмерного пространства, в котором действуют центральные силы. • Для любой центральной силы выполняется соотношение • (где - радиус-вектор с началом в центре силы), свидетельствующее о равенстве нулю момента силы относительно центра силы

Работа центральной силы • Элементарная работа силы, в том числе и центральной силы, есть скалярная величина, исчисляемая изменением энергии при перемещении точки приложения силы (в общем случае изменяющей свою величину и направление), при перемещении на столь малый отрезок своей траектории, что на нём вектор силы может считаться неизменным, то есть на расстояние : • (5) • где есть угол между этими векторами. Поскольку , то направление отсчёта угла значения не имеет.

Работа центральной силы • При перемещении на расстояние от до , весь пройденный путь можно разбить на элементарных участков. И тогда полная работа будет суммой этих элементарных работ с тем большей точностью, чем на большее количество участков будет разбита траектории, что выражается знаком интеграла, как предела этой суммы : • Рассматривая движение в Декартовой системе координат центральную силу можно представить в виде геометрической суммы её проекций на координатные оси: • Где , суть единичные векторы (орты) для своих осей.

Силовые поля • Этим полям соответствуют кулоновские силы (силы электростатического взаимодействия) и силы гравитационные (силы Всемирного тяготения. Сходство между ними заключается в том, что они могут быть обнаружены во время взаимодействия материальных объектов, причем в случае гравитации свойством, обуславливающим это взаимодействие, является масса, а в случае кулоновского взаимодействия — заряд, этой массой переносимый. Заряды, не связанные с массой, классической физике неизвестны.

Силовые поля • При сохранении подобия в геометрических размерах тел и их взаимного расстояния, силы взаимного тяготения, равно как и силы электростатические (кулоновские) растут пропорционально 4 -й степени абсолютных размеров рассматриваемой модели. В то же самое время в случае электрического взаимодействия, где между величиной заряда и размерами тел, несущих эти заряды, нет определённой связи, силы взаимодействия ослабляются пропорционально 2 -й степени абсолютных размеров. Поэтому при сравнении этих сил в микромире доминируют Кулоновские силы, а в масштабах Вселенной — силы Всемирного тяготения.

Консервативные и не консервативные силы • В физике консервати вные си лы (потенциальные силы) — силы, работа которых не зависит от формы траектории (зависит только от начальной и конечной точки приложения сил). • Отсюда следует определение: консервативные силы — такие силы, работа которых по любой замкнутой траектории равна 0. • Если в системе действуют только консервативные силы, то механическая энергия системы сохраняется. • Для консервативных сил выполняются следующие тождества: • — ротор консервативных сил равен 0;

Консервативные и не консервативные силы • — работа консервативных сил по произвольному замкнутому контуру равна 0; • — консервативная сила является градиентом некой скалярной функции , называемой силовой. Эта функция равна потенциальной энергии взятой с обратным знаком. • В школьной программе по физике силы разделяют на консервативные и неконсервативные. Примерами консервативных сил являются: сила тяжести, сила упругости. Примерами неконсервативных сил являются сила трения и сила сопротивления среды. • В теоретической физике выделяют только четыре типа сил, каждая из которых является консервативной

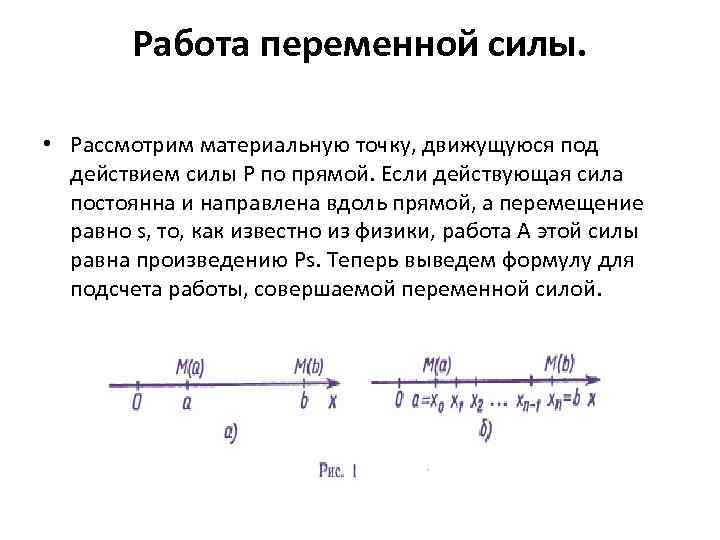Работа переменной силы. • Рассмотрим материальную точку, движущуюся под действием силы Р по прямой. Если действующая сила постоянна и направлена вдоль прямой, а перемещение равно s, то, как известно из физики, работа А этой силы равна произведению Ps. Теперь выведем формулу для подсчета работы, совершаемой переменной силой.

• Пусть точка движется по оси Ох под действием силы, проекция которой на ось Ох есть функция f от х. При этом мы будем предполагать, что f есть непрерывная функция. Под действием этой силы материальная точка переместилась из точки М (а) в точку М (b) (рис. 1, а). Покажем, что в этом случае работа А подсчитывается по формуле

• Разобьем отрезок [а; b] на п отрезков одинаковой длины . Это отрезки [а; x 1], [x 1; x 2], . . . , [xn-1; b] (рис. 1, 6). Работа силы на всем отрезке [а; b] равна сумме работ этой силы на полученных отрезках. Так как f есть непрерывная функция от x, при достаточно малом отрезке [а; x 1] работа силы на этом отрезке приблизительно равна f (а) (x 1—а) (мы пренебрегаем тем, что f на отрезке меняется). Аналогично работа силы на втором отрезке [x 1; x 2] приближенно равна f (x 1) (x 2 — x 1) и т. д. ; работа силы на n-ом отрезке приближенно равна f (xn-1)(b — xn-1). Следовательно, работа силы на всем отрезке [а; b] приближенно равна и точность приближенного равенства тем выше, чем короче отрезки, на которые разбит отрезок [а; b] Естественно, что это приближенное равенство переходит в точное, если считать, что n→∞: • Поскольку An при n →∞ стремится к интегралу рассматриваемой функции от а до b, формула (1) выведена .

Мо щность • — физическая величина, равная отношению работы, выполняемой за некоторый промежуток времени, к этому промежутку времени. • Различают среднюю мощность за промежуток времени : • и мгновенную мощность в данный момент времени: • Так как работа является мерой изменения энергии, мощность можно определить также как скорость изменения энергии системы.

Мощность в механике • Если на движущееся тело действует сила, то эта сила совершает работу. Мощность в этом случае равна скалярному произведениювектора силы на вектор скорости, с которой движется тело: • F — сила, v — скорость, — угол между вектором скорости и силы. • Частный случай мощности при вращательном движении: • M—момент силы, —угловая скорость, — число пи, n — частота вращения (число оборотов в минуту, об/мин). •

Кинетическая энергия • Кинетическая энергия вводится в механике в прямой связи с понятием работы. • Схема рассуждений такова: 1) попробуем записать работу, совершаемую всеми силами, действующими на материальную точку и, пользуясь вторым законом Ньютона (позволяющим выразить силу через ускорение), попытаться выразить ответ только через кинематические величины, 2) убедившись, что это удалось, и что этот ответ зависит только от начального и конечного состояния движения, введём новую физическую величину, через которую эта работа будет просто выражаться (это и будет кинетическая энергия). • Если — полная работа, совершённая над частицей, определяемая как сумма работ совершенных приложенными к частице силами, то она выражается как:

Кинетическая энергия • где называется кинетической энергией. Для материальной точки, кинетическая энергия определяется как работа силы, ускорившей точку от нулевой скорости до величины скорости и выражается как: • Для сложных объектов, состоящих из множества частиц, кинетическая энергия тела равна сумме кинетических энергий частиц.

Потенциальная энергия • Сила называется потенциальной, если существует скалярная функция, известная как потенциальная энергия и обозначаемая , такая что Если все силы, действующие на частицу консервативны, и является полной потенциальной энергией, полученной суммированием потенциальных энергий соответствующих каждой силе, тогда: • Этот результат известен как сохранение механической энергии и утверждает, что полная механическая энергия в замкнутой системе, в которой действуют консервативные силы • является постоянной относительно времени. Этот закон широко используется при решении задач классической механики.

Частные формы закона сохранения энергии Классическая механика • В ньютоновской механике формулируется частный случай закона сохранения энергии — Закон сохранения механической энергии, звучащий следующим образом[2] • Полная механическая энергия замкнутой системы тел, между которыми действуют только консервативные силы, остаётся постоянной. • Проще говоря, при отсутствии диссипативных сил (например, сил трения) механическая энергия не возникает из ничего и не может исчезнуть никуда. • Примеры • Классическим примером этого утверждения являются пружинный или математический маятники с пренебрежимо малым затуханием. В случае пружинного маятника в процессе колебаний потенциальная энергия деформированной пружины (имеющая максимум в крайних положениях груза) переходит в кинетическую энергию груза (достигающую максимума в момент прохождения грузом положения равновесия) и обратно[3]. В случае математического маятника[4] аналогично ведёт себя потенциальная энергия груза в поле силы тяжести.

Вывод из уравнений Ньютона • Закон сохранения механической энергии может быть выведен из второго закона Ньютона[5], если учесть, что в консервативной системе все силы, действующие на тело, потенциальны и, следовательно, могут быть представлены в виде • , • где — потенциальная энергия материальной точки ( — радиус-вектор точки пространства). В этом случае второй закон Ньютона для одной частицы имеет вид:

Вывод из уравнений Ньютона • где — масса частицы, — вектор её скорости. Скалярно домножив обе части данного уравнения на скорость частицы и приняв во внимание, что , можно получить • Путём элементарных операций это выражение может быть приведено к следующему виду

• Отсюда непосредственно следует, что выражение, стоящее под знаком дифференцирования по времени, сохраняется. Это выражение и называется механической энергией материальной точки. Первый член в сумме отвечает кинетической энергии, второй — потенциальной. • Этот вывод может быть легко обобщён на систему материальных точек

Закон сохранения полной механической энергии • Рассмотрим систему материальных точек массами , движущихся со скоростями . Пусть — равнодействующие внутренних консервативных сил, действующих на каждую из этих точек, а — равнодействующие внешних сил, которые также будем считать консервативными. Кроме того, будем считать, что на материальные точки действуют еще и внешние неконсервативные силы; равнодействующие этих сил, действующих на каждую из материальных точек, обозначим . При массы материальных точек постоянны и уравнения второго закона Ньютона для этих точек следующие:

Двигаясь под действием сил, точки системы за интервал времени совершают перемещения, соответственно равные . Умножим каждое из уравнений скалярно на соответствующее перемещение и сложим, учитывая, что . Получим:

• Первый член левой части равенства равен приращению кинетической энергии системы ( ). Второй член равен элементарной работе внутренних и внешних консервативных сил, взятой со знаком минус, т. е. равен элементарному приращению потенциальной энергии системы ( ). Правая часть равенства задает работу внешних неконсервативных сил, действующих на систему. Таким образом, имеем • При переходе системы из состояния 1 в какое-либо состояние 2

• т. е. изменение полной механической энергии системы при переходе из одного состояния в другое равно работе, совершенной при этом внешними неконсервативным силами. Если внешние неконсервативные силы отсутствуют, то Откуда т. е. полная механическая энергия системы сохраняется постоянной. Это выражение представляет собой закон сохранения механической энергии: в системе тел, между которыми действуют только консервативные силы, полная механическая энергия сохраняется, т. е. не изменяется со временем

Абсолютно упругие и не упругие соударения • Уда р — толчок, кратковременное взаимодействие тел, при котором происходит перераспределение кинетической энергии. Часто носит разрушительный для взаимодействующих тел характер. В физике под ударом понимают такой тип взаимодействия движущихся тел, при котором временем взаимодействия можно пренебречь. • При ударе выполняется закон сохранения импульса и закон сохранения момента импульса, но обычно не выполняется закон сохранения механической энергии. Предполагается, что за время удара действием внешних сил можно пренебречь, тогда полный импульс тел при ударе сохраняется, в противном случае нужно учитывать импульс внешних сил. Часть энергии обычно уходит на нагрев тел. • Результат столкновения двух тел можно полностью рассчитать, если известно их движение до удара и механическая энергия после удара. Обычно рассматривают либо абсолютно упругий удар, либо вводят коэффициент сохранения энергии k, как отношение кинетической энергии после удара к кинетической энергии до удара при ударе одного тела о неподвижную стенку, сделанную из материала другого тела. Таким образом, k является характеристикой материала, из которого изготовлены тела, и (предположительно) не зависит от остальных параметров тел (формы, скорости и т. п. ).

Абсолютно упругие и не упругие соударения • Если не известны потери энергии, происходит одновременное столкновение нескольких тел или столкновение точечных частиц, то определить однозначно движение тел после удара невозможно. В этом случае рассматривается зависимость возможных углов рассеяния и скоростей тел после удара от начальных условий. Например, при столкновении двух элементарных частиц рассеяние может произойти лишь в некотором диапазоне углов, определяющемся предельным углом рассеяния. • В общем случае решение задачи о столкновении кроме знания начальных скоростей требует дополнительных параметров.

Абсолютно упругий удар • Абсолютно упругий удар — модель соударения, при которой полная кинетическая энергия системы сохраняется. В классической механике при этом пренебрегают деформациями тел. Соответственно, считается, что энергия на деформации не теряется, а взаимодействие распространяется по всему телу мгновенно. Хорошей моделью абсолютно упругого удара является столкновение бильярдных шаров или упругих мячиков. • Абсолютно упругий удар может выполняться совершенно точно при столкновениях элементарных частиц низких энергий. Это следствие принципов квантовой механики, запрещающей произвольные изменения энергии системы. Если энергии сталкивающихся частиц недостаточно для возбуждения их внутренних степеней свободы, то механическая энергия системы не меняется. Изменение механической энергии может также быть запрещено какими-то законами сохранения (момента импульса, чётности и т. п. ). Надо, однако, учитывать, что при столкновении может изменяться состав системы. Простейший пример — излучение кванта света. Также может происходить распад или слияние частиц, а в определённых условиях — рождение новых частиц. В замкнутой системе при этом выполняются все законы сохранения, однако при вычислениях нужно учитывать изменение системы.

Абсолютно неупругий удар • Абсолю тно неупру гий удар — удар, в результате которого компоненты скоростей тел, нормальные площадке касания, становятся равными. Если удар был центральным (скорости были перпендикулярны касательной плоскости), то тела соединяются и продолжают дальнейшее своё движение как единое тело. • Как и при любом ударе, при этом выполняются закон сохранения импульса и закон сохранения момента импульса, но не выполняется закон сохранения механической энергии. Энергия, конечно же, никуда не исчезает, а переходит в тепловую. • Хорошая модель абсолютно неупругого удара — сталкивающиеся пластилиновые шарики.

• Работу выполнил Полторабатько Максим • 1 ПИ 1