Виды движений точки в динамике —

Виды движений точки в динамике -

«Вращательное движение» Основные определения и формулы

Что такое вращательное движение? Вращательное движение — вид механического движения. При вращательном движении абсолютно твёрдого тела его точки описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат при этом на одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения. Ось вращения может располагаться внутри тела и за его пределами. Ось вращения в данной системе отсчёта может быть как подвижной, так и неподвижной. Например, в системе отсчёта, связанной с Землёй, ось вращения ротора генератора на электростанции неподвижна.

Характеристики вращения тела При равномерном вращении (T оборотов в секунду), Частота вращения — число оборотов тела в единицу времени. , Период вращения — время одного полного оборота. Период вращения T и его частота ν связаны соотношением T = 1 / ν. Линейная скорость точки, находящейся на расстоянии R от оси вращения , Угловая скорость вращения тела . Момент инерции механической системы относительно неподвижной оси a ( «осевой момент инерции» ) — физическая величина. Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси: , где: mi — масса i-й точки, ri — расстояние от i-й точки до оси. Осевой момент инерции тела Ja является мерой инертности тела во вращательном движении вокруг оси a подобно тому, как массатела является мерой его инертности в поступательном движении. Кинетическая энергия вращательного движения где Iz — момент инерции тела относительно оси вращения. ω — угловая скорость

Энергия вращательного движения Кинетическая энергия вращательного движения — энергия тела, связанная с его вращением. Основные кинематические характеристики вращательного движения тела — его угловая скорость (ω) и угловое ускорение. Основные динамические характеристики вращательного движения — момент импульса относительно оси вращения z: Kz = Izωи кинетическая энергия где Iz — момент инерции тела относительно оси вращения. Похожий пример можно найти при рассмотрении вращающейся молекулы с главными осями инерции I 1, I 2 и I 3. Вращательная энергия такой молекулы задана выражением где ω1, ω2, и ω3 — главные компоненты угловой скорости. В общем случае, энергия при вращении с угловой скоростью находится по формуле: , где I — тензор инерции.

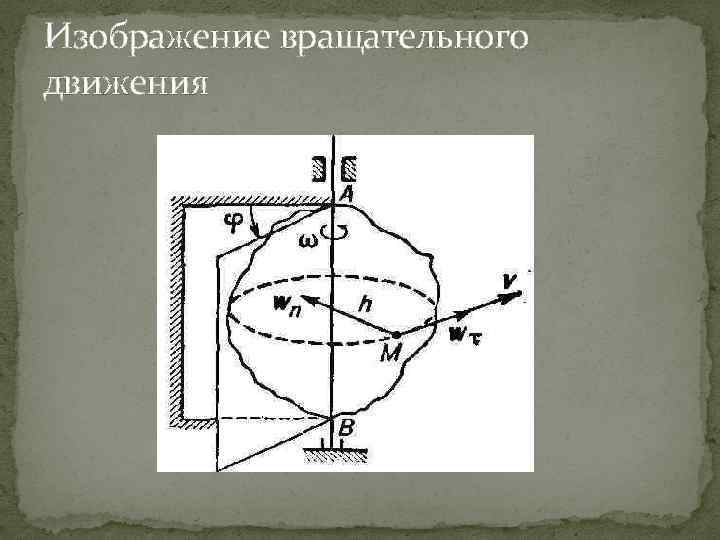Изображение вращательного движения

Поступательное движение Основные определения

Что такое поступательное движение? системы точек (тела), при котором любой отрезок прямой, связанный с движущимся телом, форма и размеры которого во время движения не меняются, остается параллельным своему положению в любой предыдущий момент времени. [1] Приведённая иллюстрация показывает, что, в отличие от распространённого утверждения [2]. поступательное движение не является противоположностью движению вращательному, а в общем случае может рассматриваться как совокупность поворотов — не закончившихся вращений. При этом подразумевается, что прямолинейное движение есть поворотвокруг бесконечно удалённого от тела центра поворота.

Примеры поступательного движения Поступательно движется, например, кабина лифта. Также, в первом приближении, поступательное движение совершает кабинаколеса обозрения. Однако, строго говоря, движение кабины колеса обозрения нельзя считать поступательным. В соответствие с первым и вторым законами Ньютона кабина, стремясь сохранить направление своего движения, отклоняется от вертикальной прямой, причём в разном направлении по разные стороны от оси симметрии колеса обозрения. Таким образом, не всякая прямая, связанная с кабиной, перемещается параллельно самой себе. Причём отклонение кабины от вертикальной прямой, и соответственно, отклонение траектории движения кабины от траектории поступательного движения тем больше, чем больше частота вращения колеса обозрения. Учитывая, что реальные частоты вращения колёс обозрения достаточно малы, траектории движения их кабин весьма близки к траектории поступательного движения. Этим можно объяснить, что во многих источниках движение кабины приводится в качестве примера поступательного движения. Моделью поступательного движения в первом приближении (если пренебречь качанием ступни) является педаль велосипеда, совершающая при этом за полный цикл своего хода один поворот вокруг своей оси.

Связь движения тела и движения его точек Если тело движется поступательно, то для описания его движения достаточно описать движение произвольной его точки (например, движение центра масс тела). Одной из важнейших характеристик движения точки является её траектория, в общем случае представляющая собой пространственную кривую, которую можно представить в виде сопряжённых дуг различного радиуса, исходящего каждый из своего центра, положение которого может меняться во времени. В пределе и прямая может рассматриваться как дуга, радиус которой равенбесконечности. Рис. 2 Пример Трёхмерного поступательного движения тела В таком случае оказывается, что при поступательном движении в каждый заданный момент времени любая точка тела совершает поворот вокруг своего мгновенного центра поворота, причём длина радиуса в данный момент одинакова для всех точек тела. Одинаковы по величине и направлению и векторы скорости точек тела, а также испытываемые ими ускорения. При решении задач теоретической механики бывает удобно рассматривать движение тела как сложение движения центра масс тела и вращательного движения самого тела вокруг центра масс (это обстоятельство принято во внимание при формулировкетеоремы Кёнига).

Примеры устройств Принцип поступательного движения реализован в чертёжном приборе — пантографе, ведущее и ведомое плечо которого всегда остаются параллельными, то есть движутся поступательно. При этом любая точка на движущихся частях совершает в плоскости заданные движения, каждая вокруг своего мгновенного центра вращения с одинаковой для всех движущихся точек прибора угловой скоростью. Существенно, что ведущее и ведомое плечо прибора, хотя и движущиеся согласно, представляют собой два разных тела. Поэтому радиусы кривизны, по которым движутся заданные точки на ведущем и ведомом плече могут быть сделаны неодинаковыми, и именно в этом и заключается смысл использования прибора, позволяющего воспроизводить любую кривую на плоскости в масштабе, определяемым отношением длин плеч. По сути дела пантограф обеспечивает синхронное поступательное движение системы двух тел: «читающего» и «пишущего» , движение каждого из которых иллюстрируется приведённым выше чертежом.

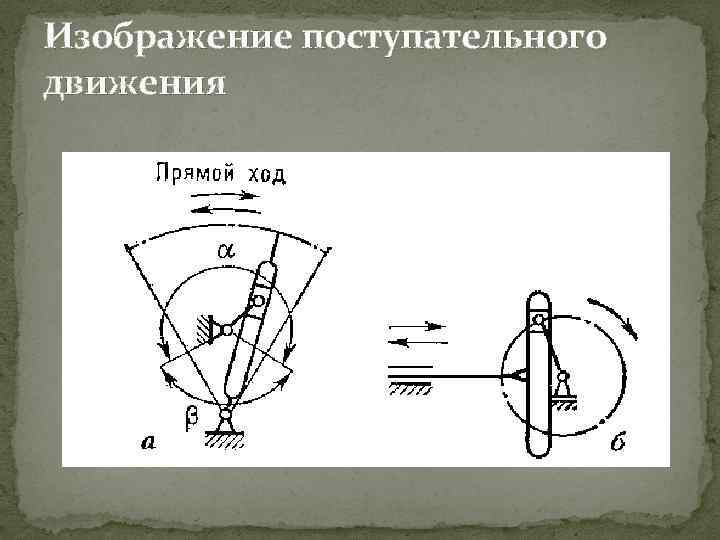Изображение поступательного движения