82c8ac6ebfd0c3340356bb36aee339f9.ppt
- Количество слайдов: 26
 Vicentiu Covrig An introduction to Derivative Instruments (Chapter 11 Reilly and Norton in the Reading Package) 1
Vicentiu Covrig An introduction to Derivative Instruments (Chapter 11 Reilly and Norton in the Reading Package) 1
 Vicentiu Covrig Potential Benefits of Derivatives Derivative instruments: Value is determined by, or derived from, the value of another instrument vehicle, called the underlying asset or security n Risk shifting - Especially shifting the risk of asset price changes or interest rate changes to another party willing to bear that risk n Price formation - Speculation opportunities when some investors may feel assets are mispriced n Investment cost reduction - To hedge portfolio risks more efficiently and less costly than would otherwise be possible 2
Vicentiu Covrig Potential Benefits of Derivatives Derivative instruments: Value is determined by, or derived from, the value of another instrument vehicle, called the underlying asset or security n Risk shifting - Especially shifting the risk of asset price changes or interest rate changes to another party willing to bear that risk n Price formation - Speculation opportunities when some investors may feel assets are mispriced n Investment cost reduction - To hedge portfolio risks more efficiently and less costly than would otherwise be possible 2
 Vicentiu Covrig Forward Contracts n n n An agreement between two parties to exchange an asset at a specified price on a specified date Buyer is long, seller is short; symmetric gains and losses as price changes, zero sum game Contracts are OTC, have negotiable terms, and are not liquid Subject to credit risk or default risk Value realized only at expiration Popular in currency exchange markets 3
Vicentiu Covrig Forward Contracts n n n An agreement between two parties to exchange an asset at a specified price on a specified date Buyer is long, seller is short; symmetric gains and losses as price changes, zero sum game Contracts are OTC, have negotiable terms, and are not liquid Subject to credit risk or default risk Value realized only at expiration Popular in currency exchange markets 3
 Vicentiu Covrig Futures Contracts n n Like forward contracts… - Buyer is long and is obligated to buy - Seller is short and is obligated to sell Unlike forward contracts… - Traded on an exchange - Standardized – size, maturity - More liquidity - can “reverse” a position and offset the future obligation, other party is the exchange - Less credit risk - initial margin required - Additional margin needs are determined through a daily “marking to market” based on price changes 4
Vicentiu Covrig Futures Contracts n n Like forward contracts… - Buyer is long and is obligated to buy - Seller is short and is obligated to sell Unlike forward contracts… - Traded on an exchange - Standardized – size, maturity - More liquidity - can “reverse” a position and offset the future obligation, other party is the exchange - Less credit risk - initial margin required - Additional margin needs are determined through a daily “marking to market” based on price changes 4
 Vicentiu Covrig Futures Contracts n Futures Quotations - One contract is for a fixed amount of the underlying asset u 5, 000 bushels of corn (of a certain grade) u$250 x Index for S&P 500 Index Futures (of a certain maturity) - Prices are given in terms of the underlying asset u. Cents per bushel (grains) u. Value of the index - Value of one contract is price x contract amount 5
Vicentiu Covrig Futures Contracts n Futures Quotations - One contract is for a fixed amount of the underlying asset u 5, 000 bushels of corn (of a certain grade) u$250 x Index for S&P 500 Index Futures (of a certain maturity) - Prices are given in terms of the underlying asset u. Cents per bushel (grains) u. Value of the index - Value of one contract is price x contract amount 5
 Vicentiu Covrig Futures Contracts Example: Suppose you bought (go long) the most recent (June) S&P 500 contract at the settle price of 1180. n What was the original contract value? Value = $250 x 1180. 80 = $295, 200 n What is your profit if you close your position (sell a contract) for 1250. 00? Value = $250 x 1250. 00 = $312, 500 Profit = $312, 500 - $295, 200 = $17, 300 6
Vicentiu Covrig Futures Contracts Example: Suppose you bought (go long) the most recent (June) S&P 500 contract at the settle price of 1180. n What was the original contract value? Value = $250 x 1180. 80 = $295, 200 n What is your profit if you close your position (sell a contract) for 1250. 00? Value = $250 x 1250. 00 = $312, 500 Profit = $312, 500 - $295, 200 = $17, 300 6
 Vicentiu Covrig Options n Option to buy is a call option Call options gives the holder the right, but not the obligation, to buy a given quantity of some asset at some time in the future, at prices agreed upon today. n Option to sell is a put option Put options gives the holder the right, but not the obligation, to sell a given quantity of some asset at some time in the future, at prices agreed upon today n n n Option premium – price paid for the option Exercise price or strike price – the price at which the asset can be bought or sold under the contract Expiration date - European: can be exercised only at expiration - American: exercised any time before expiration 7
Vicentiu Covrig Options n Option to buy is a call option Call options gives the holder the right, but not the obligation, to buy a given quantity of some asset at some time in the future, at prices agreed upon today. n Option to sell is a put option Put options gives the holder the right, but not the obligation, to sell a given quantity of some asset at some time in the future, at prices agreed upon today n n n Option premium – price paid for the option Exercise price or strike price – the price at which the asset can be bought or sold under the contract Expiration date - European: can be exercised only at expiration - American: exercised any time before expiration 7
 Vicentiu Covrig Options Contracts: Preliminaries A call option is: n n n In-the-money - The exercise price is less than the spot price of the underlying asset. At-the-money - The exercise price is equal to the spot price of the underlying asset. Out-of-the-money - The exercise price is more than the spot price of the underlying asset. 8
Vicentiu Covrig Options Contracts: Preliminaries A call option is: n n n In-the-money - The exercise price is less than the spot price of the underlying asset. At-the-money - The exercise price is equal to the spot price of the underlying asset. Out-of-the-money - The exercise price is more than the spot price of the underlying asset. 8
 Vicentiu Covrig Options Contracts: Preliminaries A put option is: n n n In-the-money - The exercise price is greater than the spot price of the underlying asset. At-the-money - The exercise price is equal to the spot price of the underlying asset. Out-of-the-money - The exercise price is less than the spot price of the underlying asset. 9
Vicentiu Covrig Options Contracts: Preliminaries A put option is: n n n In-the-money - The exercise price is greater than the spot price of the underlying asset. At-the-money - The exercise price is equal to the spot price of the underlying asset. Out-of-the-money - The exercise price is less than the spot price of the underlying asset. 9
 Vicentiu Covrig Options Example: Suppose you own a call option with an exercise (strike) price of $30. n If the stock price is $40 (in-the-money): - Your option has an intrinsic value of $10 - You have the right to buy at $30, and you can exercise and then sell for $40. n If the stock price is $20 (out-of-the-money): - Your option has no intrinsic value - You would not exercise your right to buy something for $30 that you can buy for $20! 10
Vicentiu Covrig Options Example: Suppose you own a call option with an exercise (strike) price of $30. n If the stock price is $40 (in-the-money): - Your option has an intrinsic value of $10 - You have the right to buy at $30, and you can exercise and then sell for $40. n If the stock price is $20 (out-of-the-money): - Your option has no intrinsic value - You would not exercise your right to buy something for $30 that you can buy for $20! 10
 Vicentiu Covrig Options Example: Suppose you own a put option with an exercise (strike) price of $30. n If the stock price is $20 (in-the-money): - Your option has an intrinsic value of $10 - You have the right to sell at $30, so you can buy the stock at $20 and then exercise and sell for $30 n If the stock price is $40 (out-of-the-money): - Your option has no intrinsic value - You would not exercise your right to sell something for $30 that you can sell for $40! 11
Vicentiu Covrig Options Example: Suppose you own a put option with an exercise (strike) price of $30. n If the stock price is $20 (in-the-money): - Your option has an intrinsic value of $10 - You have the right to sell at $30, so you can buy the stock at $20 and then exercise and sell for $30 n If the stock price is $40 (out-of-the-money): - Your option has no intrinsic value - You would not exercise your right to sell something for $30 that you can sell for $40! 11
 Vicentiu Covrig Options n Stock Option Quotations - One contract is for 100 shares of stock - Quotations give: u. Underlying stock and its current price u. Strike price u. Month of expiration u. Premiums per share for puts and calls u. Volume of contracts n Premiums are often small - A small investment can be “leveraged” into high profits (or losses) 12
Vicentiu Covrig Options n Stock Option Quotations - One contract is for 100 shares of stock - Quotations give: u. Underlying stock and its current price u. Strike price u. Month of expiration u. Premiums per share for puts and calls u. Volume of contracts n Premiums are often small - A small investment can be “leveraged” into high profits (or losses) 12
 Vicentiu Covrig Options Example: Suppose that you buy a January $60 call option on Hansen at a price (premium) of $9. Cost of your contract = $9 x 100 = $900 If the current stock price is $63. 20, the intrinsic value is $3. 20 per share. n What is your dollar profit (loss) if, at expiration, Hansen is selling for $50? Out-of-the-money, so Profit = ($900) n What is your percentage profit with options? Return = (0 -9)/9 = -100% n What if you had invested in the stock? Return = (50 -63. 20)/63. 20 = (20. 89%) 13
Vicentiu Covrig Options Example: Suppose that you buy a January $60 call option on Hansen at a price (premium) of $9. Cost of your contract = $9 x 100 = $900 If the current stock price is $63. 20, the intrinsic value is $3. 20 per share. n What is your dollar profit (loss) if, at expiration, Hansen is selling for $50? Out-of-the-money, so Profit = ($900) n What is your percentage profit with options? Return = (0 -9)/9 = -100% n What if you had invested in the stock? Return = (50 -63. 20)/63. 20 = (20. 89%) 13
 Vicentiu Covrig Options What is your dollar profit (loss) if, at expiration, Hansen is selling for $85? Profit = 100(85 -60) – 900 = $1, 600 n Is your percentage profit with options? Return = (85 -60 -9)/9 = 177. 78% n What if you had invested in the stock? Return = (85 -63. 20)/63. 20 = 34. 49% 14
Vicentiu Covrig Options What is your dollar profit (loss) if, at expiration, Hansen is selling for $85? Profit = 100(85 -60) – 900 = $1, 600 n Is your percentage profit with options? Return = (85 -60 -9)/9 = 177. 78% n What if you had invested in the stock? Return = (85 -63. 20)/63. 20 = 34. 49% 14
 Vicentiu Covrig Options n Payoff diagrams - Show payoffs at expiration for different stock prices (V) - for a particular option contract with a strike price of X For calls: uif the V
Vicentiu Covrig Options n Payoff diagrams - Show payoffs at expiration for different stock prices (V) - for a particular option contract with a strike price of X For calls: uif the V
 Vicentiu Covrig Option Trading Strategies There a number of different option strategies: n Buying call options n Selling call options n Buying put options n Selling put options n Option spreads 16
Vicentiu Covrig Option Trading Strategies There a number of different option strategies: n Buying call options n Selling call options n Buying put options n Selling put options n Option spreads 16
 Vicentiu Covrig Buying Call Options Position taken in the expectation that the price will increase (long position) n Profit for purchasing a Call Option: Per Share Profit =Max [0, V-X] – Call Premium n The following diagram shows different total dollar profits for buying a call option with a strike price of $70 and a premium of $6. 13 n 17
Vicentiu Covrig Buying Call Options Position taken in the expectation that the price will increase (long position) n Profit for purchasing a Call Option: Per Share Profit =Max [0, V-X] – Call Premium n The following diagram shows different total dollar profits for buying a call option with a strike price of $70 and a premium of $6. 13 n 17
 Vicentiu Covrig Buying Call Options 3, 000 Profit from Strategy 2, 500 Exercise Price = $70 2, 000 Option Price = $6. 13 1, 500 1, 000 500 0 (500) (1, 000) 40 Stock Price at Expiration 50 60 70 18 80 90 100
Vicentiu Covrig Buying Call Options 3, 000 Profit from Strategy 2, 500 Exercise Price = $70 2, 000 Option Price = $6. 13 1, 500 1, 000 500 0 (500) (1, 000) 40 Stock Price at Expiration 50 60 70 18 80 90 100
 Vicentiu Covrig Selling Call Options n n n Bet that the price will not increase greatly – collect premium income with no payoff Can be a far riskier strategy than buying the same options The payoff for the buyer is the amount owed by the writer (no upper bound on V-X) Uncovered calls: writer does not own the stock (riskier position) Covered calls: writer owns the stock 19
Vicentiu Covrig Selling Call Options n n n Bet that the price will not increase greatly – collect premium income with no payoff Can be a far riskier strategy than buying the same options The payoff for the buyer is the amount owed by the writer (no upper bound on V-X) Uncovered calls: writer does not own the stock (riskier position) Covered calls: writer owns the stock 19
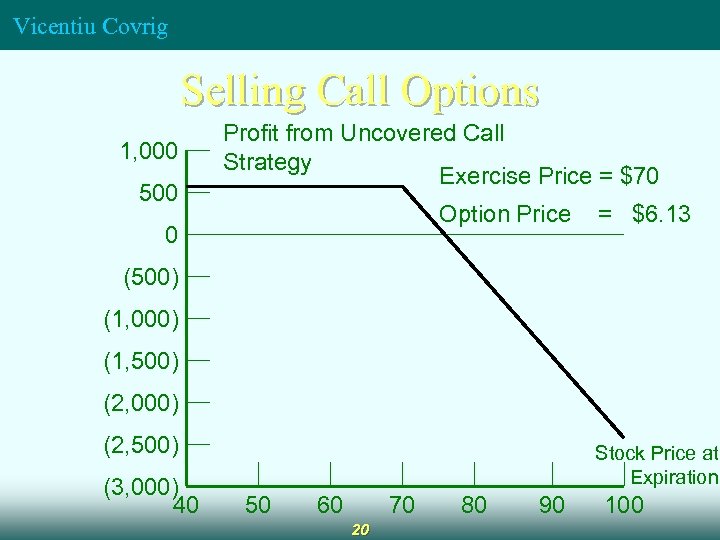 Vicentiu Covrig Selling Call Options 1, 000 500 Profit from Uncovered Call Strategy Exercise Price = $70 Option Price 0 = $6. 13 (500) (1, 000) (1, 500) (2, 000) (2, 500) (3, 000) 40 Stock Price at Expiration 50 60 70 20 80 90 100
Vicentiu Covrig Selling Call Options 1, 000 500 Profit from Uncovered Call Strategy Exercise Price = $70 Option Price 0 = $6. 13 (500) (1, 000) (1, 500) (2, 000) (2, 500) (3, 000) 40 Stock Price at Expiration 50 60 70 20 80 90 100
 Vicentiu Covrig Buying Put Options Position taken in the expectation that the price will decrease (short position) n Profit for purchasing a Put Option: Per Share Profit = Max [0, X-V] – Put Premium n Protective put: Buying a put while owning the stock (if the price declines, option gains offset portfolio losses) n 21
Vicentiu Covrig Buying Put Options Position taken in the expectation that the price will decrease (short position) n Profit for purchasing a Put Option: Per Share Profit = Max [0, X-V] – Put Premium n Protective put: Buying a put while owning the stock (if the price declines, option gains offset portfolio losses) n 21
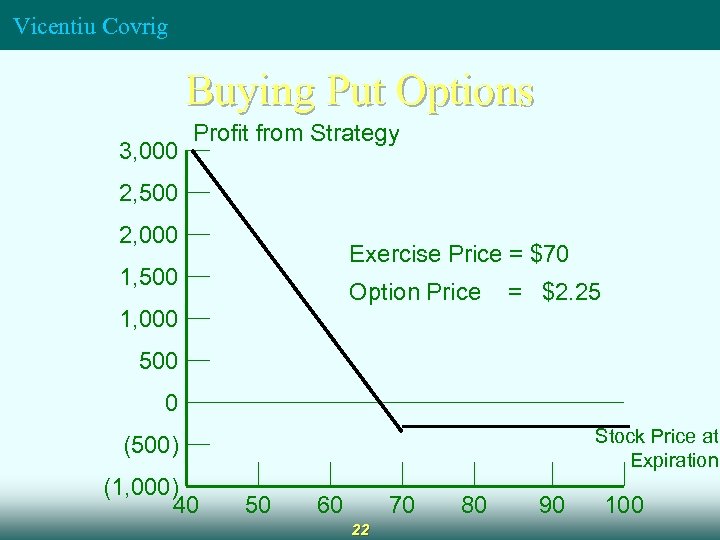 Vicentiu Covrig Buying Put Options 3, 000 Profit from Strategy 2, 500 2, 000 Exercise Price = $70 1, 500 Option Price = $2. 25 1, 000 500 0 Stock Price at Expiration (500) (1, 000) 40 50 60 70 22 80 90 100
Vicentiu Covrig Buying Put Options 3, 000 Profit from Strategy 2, 500 2, 000 Exercise Price = $70 1, 500 Option Price = $2. 25 1, 000 500 0 Stock Price at Expiration (500) (1, 000) 40 50 60 70 22 80 90 100
 Vicentiu Covrig Selling Put Options n n Bet that the price will not decline greatly – collect premium income with no payoff The payoff for the buyer is the amount owed by the writer (payoff loss limited to the strike price since the stock’s value cannot fall below zero) 23
Vicentiu Covrig Selling Put Options n n Bet that the price will not decline greatly – collect premium income with no payoff The payoff for the buyer is the amount owed by the writer (payoff loss limited to the strike price since the stock’s value cannot fall below zero) 23
 Vicentiu Covrig Selling Put Options 1, 000 Profit from Strategy 500 0 Exercise Price = $70 (500) Option Price (1, 000) = $2. 25 (1, 500) (2, 000) (2, 500) (3, 000) 40 Stock Price at Expiration 50 60 70 24 80 90 100
Vicentiu Covrig Selling Put Options 1, 000 Profit from Strategy 500 0 Exercise Price = $70 (500) Option Price (1, 000) = $2. 25 (1, 500) (2, 000) (2, 500) (3, 000) 40 Stock Price at Expiration 50 60 70 24 80 90 100
 Vicentiu Covrig Exam type question An investor bought two Google June 425 (exercise price is $425) put contracts for a premium of $20 per share. At the maturity (expiration), the Google stock price is $370. (i) Draw the payoff diagram of the investment position. (ii) Calculate the total profit/loss of the position at the expiration. 25
Vicentiu Covrig Exam type question An investor bought two Google June 425 (exercise price is $425) put contracts for a premium of $20 per share. At the maturity (expiration), the Google stock price is $370. (i) Draw the payoff diagram of the investment position. (ii) Calculate the total profit/loss of the position at the expiration. 25
 Vicentiu Covrig Learning outcomes: • discuss the benefits of using financial derivatives • know the basic characteristics of the forward and futures contracts • know the differences between forward and futures contracts (See Exhibit 11. 8) • know how to calculate the profit/loss of a futures position (numerical application) • know the basic characteristics of options • know the options’ payoffs • know how to calculate the profits/losses of a long/short call and put options (numerical application) • Recommended End-of-chapter questions: 1, 2, 5 • Recommended End-of-chapter problems: 4 a, c; 8 a, b; 9 a, c; 26
Vicentiu Covrig Learning outcomes: • discuss the benefits of using financial derivatives • know the basic characteristics of the forward and futures contracts • know the differences between forward and futures contracts (See Exhibit 11. 8) • know how to calculate the profit/loss of a futures position (numerical application) • know the basic characteristics of options • know the options’ payoffs • know how to calculate the profits/losses of a long/short call and put options (numerical application) • Recommended End-of-chapter questions: 1, 2, 5 • Recommended End-of-chapter problems: 4 a, c; 8 a, b; 9 a, c; 26
