ВФ НГТУ ИМ Р Е АЛЕКСЕЕВА Доклад на

ВФ НГТУ ИМ. Р. Е. АЛЕКСЕЕВА Доклад на тему: «Примеры применения законов распределения наработки до отказа» Руководитель: Каддо А. А. Студент: Архипов А. И.

ВВЕДЕНИЕ • Отказ – событие, заключающееся в нарушении работоспособного состояния объекта. Критерий отказа – отличительный признак или совокупность признаков, согласно которым устанавливается факт возникновения отказа. Отказы элементов могут возникать в результате первичных отказов(естественного старения), вторичных отказов(избыточные напряжения) и ошибочных команд(самопроизвольные сигналы управления и помехи). • Первичный отказ элемента определяют как нерабочее состояние этого элемента, причиной которого является он сам, и необходимо выполнить ремонтные работы для возвращения элемента в рабочее состояние. • Вторичный отказ - такой же, как первичный, за исключением того, что сам элемент не является причиной отказа. Вторичные отказы объясняются воздействием предыдущих или текущих избыточных напряжений на элементы. • Инициированные отказы (ошибочные команды). Люди, например, операторы и обслуживающий технический персонал, также являются возможными источниками вторичных отказов, если их действия приводят к выходу элементов из строя. Ошибочные команды представляются в виде элемента, находящегося в нерабочем состоянии из-за неправильного сигнала управления или помех (при этом лишь иногда требуется ремонт для возвращения данного элемента в рабочее состояние). Самопроизвольные сигналы управления или помехи часто не оставляют последствий (повреждений), и в нормальных последующих режимах элементы работают в соответствии с заданными требованиями. • Наработка до отказа - наработка объекта от начала эксплуатации до возникновения первого отказа.

ЗАКОНЫ РАСПРЕДЕЛЕНИЯ НАРАБОТКИ ДО ОТКАЗА: ЭКСПОНЕНЦИАЛЬНЫЙ, ЛОГНОРМАЛЬНЫЙ И ГАММАРАСПРЕДЕЛЕНИЕ

1. ЭКСПОНЕНЦИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ • Экспоненциальное распределение описывает наработку до отказа объектов, у которых в результате сдаточных испытаний (выходного контроля) отсутствует период приработки, а назначенный ресурс установлен до окончания периода нормальной эксплуатации. • Эти объекты можно отнести к «не стареющим» , поскольку они работают только на участке с λ (t) = = const. Круг таких объектов широк: сложные технические системы с множеством компонентов, средства вычислительной техники и системы автоматического регулирования и т. п. Экспоненциальное распределение широко применяется для оценки надежности энергетических объектов.

• Считается, что случайная величина наработки объекта до отказа подчинена экспоненциальному распределению, если ПРО описывается выражением: • • f(t) = exp( - t), • • где – параметр распределения, который по результатам испытаний принимается равным • α 1 / Т 0 , • • где 0 – оценка средней наработки до отказа.

• График изменения показателей безотказности при экспоненциальном распределении.

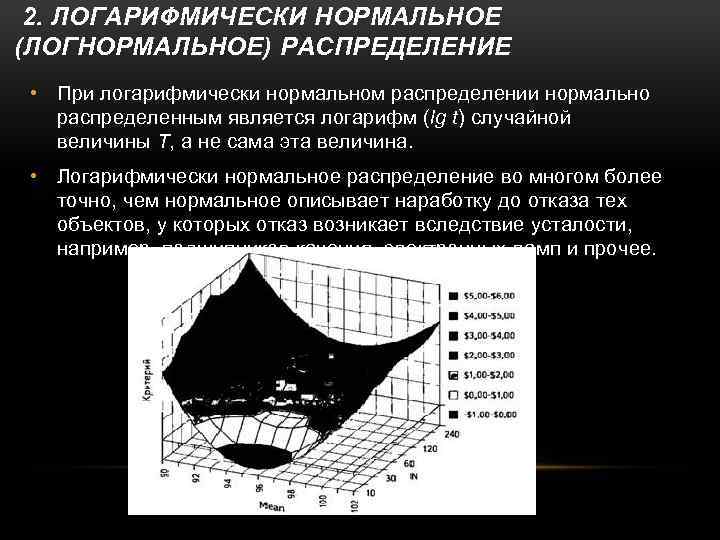2. ЛОГАРИФМИЧЕСКИ НОРМАЛЬНОЕ (ЛОГНОРМАЛЬНОЕ) РАСПРЕДЕЛЕНИЕ • При логарифмически нормальном распределении нормально распределенным является логарифм (lg t) случайной величины T, а не сама эта величина. • Логарифмически нормальное распределение во многом более точно, чем нормальное описывает наработку до отказа тех объектов, у которых отказ возникает вследствие усталости, например, подшипников качения, электронных ламп и прочее.

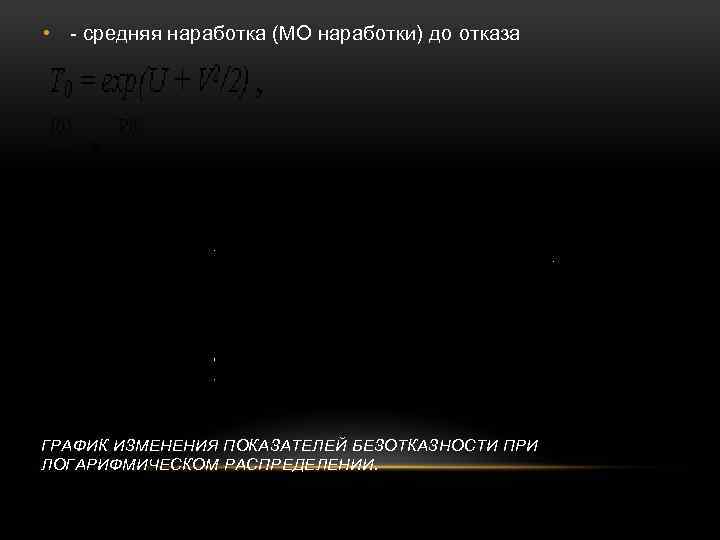• - средняя наработка (МО наработки) до отказа ГРАФИК ИЗМЕНЕНИЯ ПОКАЗАТЕЛЕЙ БЕЗОТКАЗНОСТИ ПРИ ЛОГАРИФМИЧЕСКОМ РАСПРЕДЕЛЕНИИ.

• В статистике так называемое логнормальное распределение применяется в том случае, когда начинает изменяться цена актива в будущем - а это случайный процесс, который в принципе должен описываться нормальным распределением. В то же время для целей вероятностной оценки стоимости актива в теории пользуются не нормальным, а логнормальным распределением.

3. ГАММА РАСПРЕДЕЛЕНИЕ • Гамма-распределение наиболее хорошо описывает распределение суммы независимых случайных величин, каждая из которых распределена по экспоненциальному закону. • При больших гамма-распределение сходится к нормальному распределению с параметрами: a = β · α , b = β · α 2. • Средняя наработка (МО наработки) до отказа: • T 0 =β/α • Гамма-распределению подчинены во многих ситуациях такие величины, как общий срок службы изделия, длина цепочки токопроводящих пылинок, время достижения изделием предельного состояния при коррозии, время наработки до k-го отказа, k = 1, 2, …, и т. д.

ГРАФИК ИЗМЕНЕНИЯ ПОКАЗАТЕЛЕЙ БЕЗОТКАЗНОСТИ ПРИ ЛОГАРИФМИЧЕСКОМ РАСПРЕДЕЛЕНИИ.

• В статистике широко используется гамма-распределение, частными случаями которого являются экспоненциальное распределение и распределение хи-квадрат. • Особенности применения рассматриваемых критериев заключаются в том, что предельные распределения статистик критериев в данном случае зависят от значения параметра формы гамма-распределения. Кроме того, модели распределений статистик при проверке согласия с гаммараспределением построены только для случая использования ОМП и для ограниченного ряда значений параметра формы.

Пример применения законов и коэффициента надежности на примере светодиода

СПАСИБО ЗА ВНИМАНИЕ