Скачать презентацию Vertical Graph Analytics summarizes Sat Notes 06_15 -pres Скачать презентацию Vertical Graph Analytics summarizes Sat Notes 06_15 -pres

f0fc996b45bfb8f6407b13ba2e9af402.ppt

  • Количество слайдов: 60

Vertical Graph Analytics (summarizes Sat. Notes 06_15 -pres) Most complex data is modelled as Vertical Graph Analytics (summarizes Sat. Notes 06_15 -pres) Most complex data is modelled as a graph or hypergraph (a table is a graph without edges, so ALL data is modelled as a graph!). We strive for max speed and accuracy in our graph analytics by using vertical structure. We consider the following topics: 1. Vertical structuring of graph data (Edge p. Tree (E), Path. Ptree (PP), Shortest. Path. Trees…). 2. Connectivity Component Partitioning. 3. Community Mining (k-plexes, which include cliques as 0 -plexes; k-cores, Density-communities, Degree-communities, 4. Community existence theorems (determine if a given Induced Sub. Graph is a community) and community mining algorithms (find all communities) include: Vertex Count based Existence Thms. Inheritance (downward or upward closure based existence thms). Density Difference. Degree Difference. 5. Graph and Hyper. Graph Clustering (Community based, Vertex betweenness, Edge betweenness Clustering). 6. Multi. PART graphs, Hyper. Graphs, Multi. PART Hypergraphs nnd the Clique Tree construct (c. Tree) for Multi. PART graphs and hypergraphs. PP(G), the Path Ptree of graph, G, is a vertical representation of all paths in G and is used to find diameter, shortest paths, communities, motifs. . . By modifying data structures (from horizontal to vertical) the analytics fit hardware strengths and allow do NP-hard/complete problems. A Path is a sequence of edges connecting a sequence of vertices, distinct except for end-vertices. A Simple Path (assumed) excludes loops, (v, v). We’ll always program using the pop-count (produces 1 -counts during ANDs/ORs for free, timewise). C is a clique iff all C level 1 counts are |VC|-1. COMMUNITIES (=~ a subgraph with more edges than expected): A k-plex is a [max] subgraph in which each vertex is adjacent to all subgraph vertices except at most k of them. A 0 -plex is called a clique. A k-core is a [max] subgraph in which each vertex is adjacent to at least k subgraph vertices. An n-clique is a [max] subgraph s. t. the geodesic distance between any vertex pair is n. An n-clan is a [max] n-clique with diameter n. An n-club is [max] subgraph of diam=n. v C, kvint =#edges v to C; kvext=#edges v to C’. Int. Deg(C) k. Cint = v C kvint Ext. Deg(C), k. Cext = v C kvext Internal. Density of C δint(C)=|edges(C, C)|/(nc(nc− 1)/2) External Density of C δext(C)= edges(C, C’)|/(nc(n-nc)). Ext. Den. C*n(n-n. C)/2=Ext. Deg. C Int. Den. C<Thresh? Degree Difference k. Cint – k. Cext > Thresh? Easy to compute even for Big Graphs. Giant Yahoo Data Dump Aims to Help Computers Know What You Want: (see “Here’s What Developers Are Doing With Google’s AI Brain”).

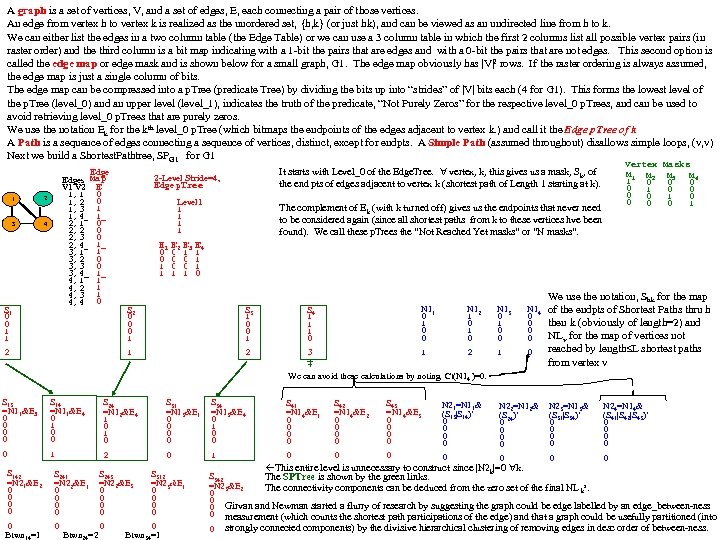A graph is a set of vertices, V, and a set of edges, E, A graph is a set of vertices, V, and a set of edges, E, each connecting a pair of those vertices. An edge from vertex h to vertex k is realized as the unordered set, {h, k} (or just hk), and can be viewed as an undirected line from h to k. We can either list the edges in a two column table (the Edge Table) or we can use a 3 column table in which the first 2 columns list all possible vertex pairs (in raster order) and the third column is a bit map indicating with a 1 -bit the pairs that are edges and with a 0 -bit the pairs that are not edges. This second option is called the edge map or edge mask and is shown below for a small graph, G 1. The edge map obviously has |V|2 rows. If the raster ordering is always assumed, the edge map is just a single column of bits. The edge map can be compressed into a p. Tree (predicate Tree) by dividing the bits up into “strides” of |V| bits each (4 for G 1). This forms the lowest level of the p. Tree (level_0) and an upper level (level_1), indicates the truth of the predicate, “Not Purely Zeros” for the respective level_0 p. Trees, and can be used to avoid retrieving level_0 p. Trees that are purely zeros. We use the notation Ek for the kth level_0 p. Tree (which bitmaps the endpoints of the edges adjacent to vertex k. ) and call it the Edge p. Tree of k A Path is a sequence of edges connecting a sequence of vertices, distinct, except for endpts. A Simple Path (assumed throughout) disallows simple loops, (v, v) Next we build a Shortest. Pathtree, SPG 1 for G 1 1 2 3 Edges Map V 1 V 2 E 1, 1 0 1, 2 0 1, 3 1 1, 4_ 1_ 2, 1 0 2, 2 0 2, 3 0 2, 4_ 1_ 3, 1 1 3, 2 0 3, 3 0 3, 4_ 1_ 4, 1 1 4, 2 1 4, 3 1 4, 4 0 4 2 -Level Stride=4, Edge p. Tree It starts with Level_0 of the Edge. Tree. vertex, k, this gives us a mask, Sk, of the end pts of edges adjacent to vertex k (shortest path of Length 1 starting at k). Level 1 1 1 The complement of Ek (with k turned off) gives us the endpoints that never need to be considered again (since all shortest paths from k to these vertices hve been found). We call these p. Trees the “Not Reached Yet masks” or “N masks”. E 1 0 0 1 1 E 2 E 3 0 1 0 0 1 1 E 4 1 1 1 0 2 S 2 0 0 0 1 S 3 1 0 0 1 S 4 1 1 1 0 N 11 0 0 N 12 1 0 N 13 0 1 0 0 1 S 1 0 0 1 1 Vertex Masks M 1 M 2 M 3 M 4 1 0 0 0 0 0 1 0 2 3 1 2 1 We use the notation, Shk for the map N 14 of the endpts of Shortest Paths thru h 0 then k (obviously of length=2) and 0 0 NLv for the map of vertices not 0 reached by length L shortest paths 0 from vertex v We can avoid these calculations by noting Ct(N 14 )=0. S 13 =N 11&E 3 0 0 S 14 =N 11&E 4 0 1 0 0 S 24 =N 12&E 4 1 0 S 31 =N 13&E 1 0 0 S 34 =N 13&E 4 0 1 0 0 0 1 2 0 1 S 142 =N 21&E 2 0 0 S 241 =N 22&E 1 0 0 S 243 =N 22&E 3 0 0 S 312 =N 23&E 1 0 0 0 0 Btwn 14=1 Btwn 24=2 Btwn 34=1 S 41 =N 14&E 1 0 0 S 42 =N 14&E 2 0 0 S 43 =N 14&E 3 0 0 N 21=N 11& (S 13|S 14)’ 0 0 N 22=N 12& (S 24)’ 0 0 N 23=N 13& (S 31|S 34)’ 0 0 N 24=N 14& (S 41|S 42|S 43)’ 0 0 0 This entire level is unnecessary to construct since |N 2 k|=0 k. The SPTree is shown by the green links. The connectivity components can be deduced from the zero set of the final NL ks. S 342 =N 23&E 2 0 0 0 Girvan and Newman started a flurry of research by suggesting the graph could be edge labelled by an edge_between-ness 0 measurement (which counts the shortest path participations of the edge) and that a graph could be usefully partitioned (into 0 strongly connected components) by the divisive hierarchical clustering of removing edges in desc order of between-ness.

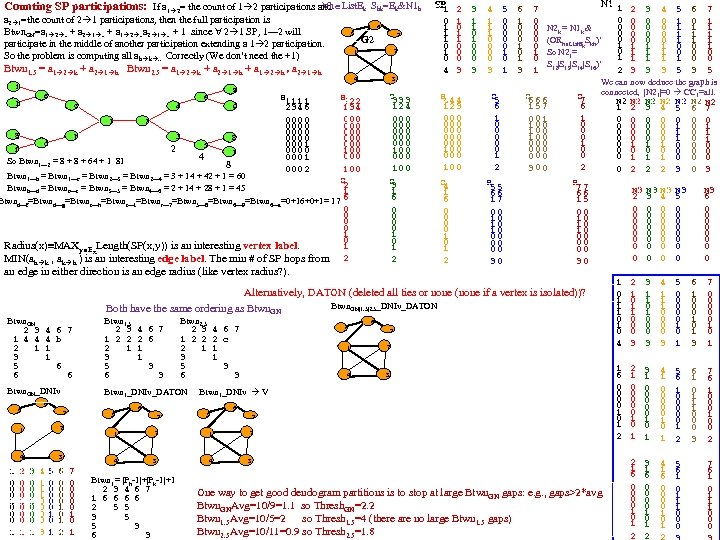h List. Ek Shk=Ek&N 1 h Counting SP participations: If a 1 2= h List. Ek Shk=Ek&N 1 h Counting SP participations: If a 1 2= the count of 1 2 participations and a 2 1=the count of 2 1 participations, then the full participation is Btwn. GN=a 1 2. . + a 2 1. . + a 1 2. . a 2 1. . + 1 since 2 1 SP, 1— 2 will participate in the middle of another participation extending a 1 2 participation. So the problem is computing all ah k. . Correctly (We don’t need the +1) 5 e a 2 4 3 S 33 3 12 4 00 0 00 0 10 0 S 3 1 6 0 0 1 0 1 2 S 22 2 13 4 00 0 1 2 00 0 g b 3 8 00 0 d 00 0 5 2 f 10 0 7 00 0 4 So Btwn 1— 2 = 8 + 64 + 1 81 8 10 0 Btwn 1—b = Btwn 1—c = Btwn 2— 3 = Btwn 2— 4 = 3 + 14 + 42 + 1 = 60 S 2 Btwnb—d = Btwnc—e = Btwn 3— 5 = Btwn 4— 6 = 2 + 14 + 28 + 1 = 45 1 6 Btwnd—f=Btwnd—g=Btwne—h=Btwne—i=Btwnr— 7=Btwn 5— 8=Btwn 6— 9=Btwn 6—a=0+16+0+1= 17 0 0 1 0 Radius(x) MAXy Ex. Length(SP(x, y)) is an interesting vertex label. 1 MIN(ah k , ak h ) is an interesting edge label. The min # of SP hops from 2 h 6 c S 1 1 23 4 6 00 0 0 00 0 1 00 0 0 00 0 1 00 0 2 9 4 7 1 Btwn 1. 5 = a 1 2 k + a 2 1 h Btwn 2. 5 = a 1 2 k + a 2 1 h + a 1 2 h * a 2 1 h i 6 G 2 an edge in either direction is an edge radius (like vertex radius? ). 4 6 7 4 b 1 1 6 6 Btwn. GN_DNIv 7 4 5 3 3 0 0 0 1 4 1 1 1 0 0 3 5 0 0 0 1 4 6 7 2 6 1 1 3 3 Btwn 2. 5 2 3 1 2 2 2 1 3 5 6 Btwn 1_DNIv_DATON 2 2 0 0 0 1 Btwn 1. 5 2 3 1 2 2 2 1 3 5 6 6 1 1 0 0 0 1 0 1 1 1 0 4 1 0 1 1 0 0 0 3 S 44 4 12 3 00 0 00 0 10 0 S 4 1 6 0 0 1 0 1 2 1 1 0 0 0 3 4 1 1 1 0 0 3 5 0 0 0 1 S 5 6 1 0 0 0 1 2 S 55 66 17 00 10 10 10 00 00 00 30 6 1 0 0 0 1 3 7 0 0 0 1 N 1 1 2 3 4 5 6 7 0 0 1 0 0 0 0 1 1 1 N 2 k = N 1 k & 0 0 1 1 1 (ORh List. Ek. Skh)’ 0 0 1 1 1 1 0 0 0 So N 21= 1 1 1 0 0 S 12|S 13|S 14|S 16)’ 2 3 3 3 5 We can now deduce the graph is connected, |N 21|=0 CC 1=all. S 6 S 7 6 6 N 2 N 2 6 157 1 2 3 4 5 6 7 1 001 0 0 0 0 100 0 0 0 0 1 0 1 0 100 0 0 1 1 000 0 1 1 1 0 0 000 0 000 0 1 1 1 0 0 0 2 300 0 2 2 2 3 0 3 S 77 N 3 N 3 N 3 66 2 3 4 5 6 15 0 0 00 0 0 10 0 0 0 0 0 00 0 0 30 Alternatively, DATON (deleted all ties or none (none if a vertex is isolated))? Btwn. GN|1. 5|2. 5_DNIv_DATON Both have the same ordering as Btwn. GN 2 3 1 4 4 2 1 3 5 6 5 SP 2 3 1 6 0 0 1 0 1 2 6 7 4 6 7 2 c 1 1 3 3 5 7 1 2 4 3 Btwn 1_DNIv V 5 6 7 1 2 4 7 0 0 0 1 6 3 4 3 Btwn 1 = |Ph-1|+|Pk-1|+1 2 3 4 6 7 1 6 6 2 5 5 3 6 3 One way to get good dendogram partitions is to stop at large Btwn. GN gaps: e. g. , gaps>2*avg Btwn. GNAvg=10/9=1. 1 so Thresh. GN=2. 2 Btwn 1. 5 Avg=10/5=2 so Thresh 1. 5=4 (there are no large Btwn 1. 5 gaps) Btwn 2. 5 Avg=10/11=0. 9 so Thresh 2. 5=1. 8 1 0 1 1 1 0 4 2 1 0 1 1 0 0 0 3 3 1 1 0 0 0 3 4 1 1 1 0 0 3 5 0 0 0 1 6 1 0 0 0 1 3 7 0 0 0 1 1 6 0 0 1 0 1 2 2 1 0 0 0 1 3 1 0 0 0 1 4 1 0 0 0 1 5 6 1 0 0 0 1 2 6 1 0 1 1 1 0 0 0 3 7 6 1 0 0 0 1 0 0 2 2 1 6 0 0 1 0 1 2 3 1 6 0 0 1 0 1 2 4 1 6 0 0 1 0 1 5 6 1 0 1 1 1 0 0 0 7 6 1 0 1 1 1 0 0 0

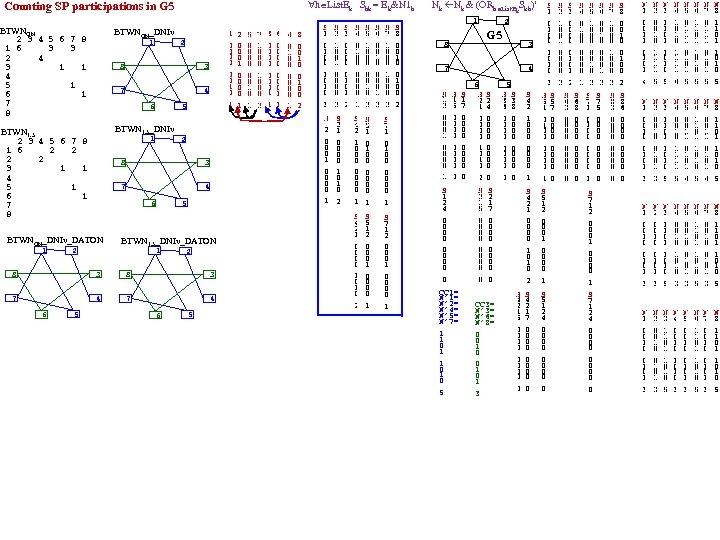h List. Ek Shk = Ek&N 1 h Counting SP participations in G h List. Ek Shk = Ek&N 1 h Counting SP participations in G 5 BTWNGN 2 3 4 5 6 7 8 1 6 3 3 2 4 3 1 1 4 5 1 6 1 7 8 BTWN 1. 5 2 3 4 5 6 7 8 1 6 2 2 3 1 1 4 5 1 6 1 7 8 BTWN 1. 5_DNIv 1 1 2 8 3 7 4 5 6 BTWNGN_DNIv_DATON BTWN 1. 5_DNIv_DATON 1 2 1 0 0 0 1 0 1 2 8 3 7 4 6 5 2 0 0 0 1 5 0 0 0 1 0 1 7 1 0 0 0 2 3 0 0 0 0 1 1 6 0 0 0 0 1 1 4 0 1 0 0 0 1 8 0 0 1 0 0 2 S 1 0 0 1 0 3 S 2 1 0 0 0 0 2 S 1 2 0 0 0 1 BTWNGN_DNIv S 2 1 0 0 1 0 2 S 3 0 0 0 1 2 S 4 0 1 0 0 0 1 S 5 1 0 0 0 1 0 2 S 6 0 0 1 2 S 7 1 0 0 0 2 S 4 2 1 0 0 0 0 1 S 5 1 0 0 0 0 1 S 7 1 0 0 0 0 1 S 4 2 1 0 0 1 0 2 S 5 1 2 0 0 0 1 S 7 1 2 0 0 0 1 S 8 0 0 1 0 0 2 Nk Nk & (ORh List. Ek. Skh)’ 1 2 G 5 8 3 4 7 5 6 S 1 2 0 0 0 1 S 1 0 0 1 0 3 S 1 5 0 0 0 0 0 S 1 2 4 0 0 0 0 0 CC 1= N’ 2= N’ 4= N’ 5= N’ 7= 1 1 0 1 0 5 S 1 7 0 0 0 0 0 S 2 1 0 0 1 0 2 S 2 4 0 0 0 0 0 S 2 1 5 0 0 0 0 0 S 2 1 7 0 0 0 0 0 CC 3= N’ 6= N’ 8= 0 0 1 0 1 3 S 3 6 0 0 0 0 0 S 3 8 0 0 0 0 0 S 4 2 1 0 0 0 0 1 S 4 2 1 0 0 1 0 2 S 4 2 1 5 0 0 0 0 0 S 5 1 0 0 0 0 1 S 5 1 2 0 0 0 1 S 4 2 1 7 0 0 0 0 0 S 5 1 2 4 0 0 0 0 0 S 5 7 0 0 0 0 0 S 2 1 0 0 0 0 2 S 3 0 0 0 1 2 S 6 3 0 0 0 0 0 S 4 0 1 0 0 0 1 S 6 8 0 0 0 0 0 S 5 1 0 0 0 1 0 2 S 7 1 0 0 0 0 1 S 7 1 2 0 0 0 1 S 7 1 2 4 0 0 0 0 0 S 6 0 0 1 2 S 7 5 0 0 0 0 0 S 7 1 0 0 0 2 S 8 0 0 1 0 0 2 N 1 0 0 1 1 0 1 4 N 2 0 0 1 1 1 1 5 N 3 1 1 0 1 0 5 N 4 1 0 1 1 6 N 5 0 1 1 1 0 1 5 N 6 1 1 0 1 0 5 N 7 0 1 1 1 0 1 5 N 8 1 1 0 1 0 5 S 8 3 0 0 0 0 0 S 8 6 0 0 0 0 0 N 1 0 0 1 0 1 3 N 2 0 0 1 0 1 3 N 3 1 1 0 1 0 5 N 4 0 0 1 1 1 1 5 N 5 0 0 1 1 0 1 4 N 6 1 1 0 1 0 5 N 7 0 0 1 1 0 1 4 N 8 1 1 0 1 0 5 N 1 0 0 1 0 1 3 N 2 0 0 1 0 1 3 N 3 1 1 0 1 0 5 N 4 0 0 1 0 1 0 1 0 3 N 5 0 0 1 0 1 3 N 6 1 1 0 1 0 5 N 7 0 0 1 0 1 3 N 8 1 1 0 1 0 5

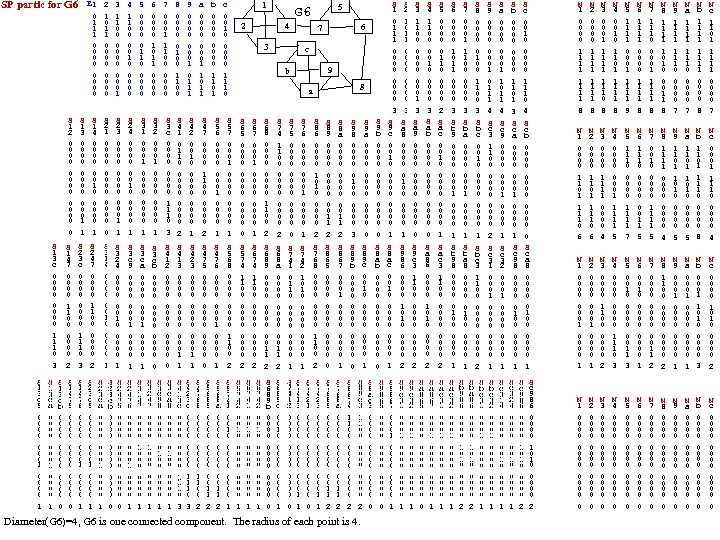SP partic for G 6 S 1 2 0 0 0 0 S 1 SP partic for G 6 S 1 2 0 0 0 0 S 1 3 c 0 0 0 0 1 1 1 0 3 S 1 3 c 9 0 0 0 0 1 S 1 3 c a 0 0 0 0 1 S 1 4 7 0 0 1 1 0 0 0 2 S 1 3 c b 0 0 0 0 S 1 4 7 5 0 0 0 0 E 1 2 0 1 1 1 1 0 0 0 0 S 1 3 0 0 0 1 1 3 1 1 0 0 0 0 0 1 4 1 1 0 0 0 0 0 5 0 0 0 1 1 0 0 0 6 0 0 1 0 1 1 0 0 S 2 1 0 0 0 0 S 2 3 0 0 0 1 1 S 2 4 0 0 0 1 S 3 1 0 0 0 1 S 3 2 0 0 0 1 0 0 0 0 1 S 3 1 4 0 0 0 1 S 3 2 4 0 0 0 1 S 3 c 9 0 0 0 0 1 S 3 c a 0 0 0 0 1 S 3 c b 0 0 0 0 S 2 4 7 5 0 0 0 0 S 2 4 7 6 0 0 0 0 1 S 1 4 0 0 0 1 S 2 3 c 0 0 0 0 1 1 1 0 3 S 2 4 7 0 0 1 1 0 0 0 2 S 1 4 7 6 0 0 0 0 1 S 2 3 c 9 0 0 0 0 1 S 2 3 c a 0 0 0 0 1 S 2 3 c b 0 0 0 0 S 3 1 4 7 0 0 1 0 0 0 0 1 S 3 2 4 7 0 0 1 0 0 0 0 1 7 0 0 0 1 1 1 0 0 0 S 3 c 9 8 0 0 0 1 b 0 0 0 0 1 1 9 0 0 0 0 1 1 1 S 3 c 0 0 0 0 1 1 1 0 3 S 4 1 0 1 1 0 0 0 0 0 2 S 4 2 0 0 1 0 0 0 0 0 1 S 4 7 0 0 1 1 0 0 0 2 S 5 6 0 0 0 0 1 S 5 7 0 0 0 1 0 0 0 0 1 S 6 5 0 0 0 0 S 6 7 0 0 0 1 0 0 0 0 1 S 6 8 0 0 0 0 1 1 0 0 2 S 7 4 1 1 0 0 0 0 0 2 S 7 5 0 0 0 0 S 7 6 0 0 0 0 1 S 8 6 0 0 1 0 0 0 2 S 8 9 0 0 0 0 0 1 1 2 S 8 a 0 0 0 0 0 1 1 2 S 9 8 0 0 0 1 0 0 0 3 S 9 a 0 0 0 0 S 4 1 2 0 0 0 0 S 4 1 3 0 0 0 1 1 S 4 2 3 0 0 0 1 1 S 4 7 5 0 0 0 0 S 4 7 6 0 0 0 0 1 S 5 6 8 0 0 0 0 1 1 0 0 2 S 5 7 4 1 1 0 0 0 0 0 2 S 6 8 9 0 0 0 0 0 1 1 2 S 6 8 a 0 0 0 0 0 1 1 2 S 7 4 1 0 1 1 0 0 0 0 0 1 S 7 4 2 1 0 0 0 0 0 1 S 7 6 8 0 0 0 0 1 1 0 0 2 S 8 6 5 0 0 0 0 S 8 6 7 0 0 0 1 0 0 0 0 1 S 8 9 b 0 0 0 0 S 8 9 c 0 0 1 0 0 0 0 0 1 S 3 c a 8 0 0 0 1 S 4 1 3 c 0 0 0 0 1 1 1 0 3 S 5 6 8 a 0 0 0 0 0 1 1 2 S 5 7 4 1 0 0 0 1 S 6 8 9 b 0 0 0 0 S 6 8 9 c 0 0 1 0 0 0 0 0 1 S 7 4 1 2 0 0 0 0 S 7 6 8 9 0 0 0 0 0 1 1 2 S 7 6 8 a 0 0 0 0 0 1 1 2 S 4 2 3 c 0 0 0 0 1 1 1 0 3 a 0 0 0 0 1 1 S 4 7 6 8 0 0 0 0 1 1 0 0 2 S 5 6 8 9 0 0 0 0 0 1 1 2 c 0 0 1 0 0 0 1 1 1 0 4 S 6 7 4 2 0 0 1 0 0 0 0 0 1 S 5 0 0 0 1 1 0 0 0 2 S a c 0 0 1 0 0 0 0 0 1 S 6 0 0 1 0 1 1 0 0 3 S b 9 0 0 0 0 1 S 8 a c 0 0 1 0 0 0 0 0 1 S 9 8 6 0 0 1 0 0 0 2 S 9 c 3 1 1 0 0 0 0 0 2 S a 8 6 0 0 1 0 0 0 2 S a c 3 1 1 0 0 0 0 0 2 S b 9 8 0 0 0 1 S 9 8 6 7 0 0 0 1 0 0 0 0 1 S 9 c 3 1 0 0 0 0 0 0 0 0 1 S a c 3 2 0 0 0 1 0 0 0 0 1 9 8 a S 6 7 4 1 0 0 0 1 S 4 1 1 0 0 0 0 0 3 S a b 0 0 0 0 c b S 5 7 4 2 0 0 1 0 0 0 0 0 1 S 9 b 0 0 0 0 S 3 1 1 0 0 0 0 0 1 3 S a 9 0 0 0 0 6 7 3 S 2 1 0 1 1 0 0 0 0 3 S a 8 0 0 0 1 5 G 6 2 S 1 0 1 1 1 0 0 0 0 3 S 9 c 0 0 1 0 0 0 0 0 1 S 8 a b 0 0 0 0 8 0 0 0 1 1 0 0 S 7 4 1 3 0 0 0 1 1 S 7 4 2 1 0 0 0 0 S 7 4 2 3 0 0 0 1 1 S 8 6 7 4 1 1 0 0 0 0 0 2 S 8 9 c 3 1 1 0 0 0 0 0 2 Diameter(G 6)=4, G 6 is one connected component. The radius of each point is 4. S 8 a c 3 0 0 0 0 S 9 8 6 5 0 0 0 0 S 9 c 3 2 0 0 0 1 0 0 0 0 1 S a 8 6 5 0 0 0 0 S a 8 6 7 0 0 0 1 0 0 0 0 1 S 7 0 0 0 1 1 1 0 0 0 3 N 1 0 0 1 1 1 1 8 S 9 0 0 0 0 1 1 1 4 S a 0 0 0 0 1 1 4 S b 0 0 0 0 1 1 0 1 3 S c 0 0 1 0 0 0 1 1 1 0 4 S b a 0 0 0 0 1 S 8 0 0 0 1 1 0 0 3 S b c 0 0 1 0 0 0 0 0 1 S c 3 1 1 0 0 0 0 0 2 S c 9 0 0 0 0 1 S c a 0 0 0 0 1 S b a 8 0 0 0 1 S b c 3 1 1 0 0 0 0 0 2 S c 3 1 0 0 0 1 S c 3 2 0 0 0 1 0 0 0 0 1 S c 9 8 0 0 0 1 S c b 0 0 0 0 S c a 8 0 0 0 1 S b c 3 2 0 0 0 1 0 0 0 0 1 S c 3 1 4 0 0 0 1 S b 9 8 6 0 0 1 0 0 0 2 S b a 8 6 0 0 1 0 0 0 2 S b c 3 1 0 0 0 1 S c 3 2 4 0 0 0 1 S c 9 8 6 0 0 0 0 1 0 1 0 0 0 0 0 2 N 2 0 0 1 1 1 1 8 N 3 0 0 0 1 1 1 1 0 8 N 4 0 0 1 1 1 8 N 5 1 1 0 0 0 1 1 1 9 N 6 1 1 0 0 1 1 8 N 7 1 1 1 0 0 1 1 1 8 N 8 1 1 1 0 0 0 1 1 8 N 9 1 1 1 1 0 0 0 7 N a 1 1 1 1 0 0 0 7 N b 1 1 1 1 0 0 8 N c 1 1 0 1 1 1 0 0 7 N 1 0 0 1 1 0 6 N 2 0 0 1 1 0 6 N 3 0 0 1 1 0 0 4 N 4 0 0 0 0 1 1 1 5 N 5 1 1 1 0 0 0 1 1 7 N 6 1 1 1 0 0 0 0 1 1 5 N 7 0 0 1 0 0 0 1 1 5 N 8 1 1 0 0 0 0 4 N 9 1 1 0 1 0 0 0 5 N a 1 1 0 1 0 0 0 5 N b 1 1 0 0 0 8 N c 0 0 0 1 1 0 0 0 4 N 1 0 0 0 0 1 N 2 0 0 0 0 1 N 3 0 0 1 1 0 0 0 2 N 4 0 0 0 0 1 1 1 0 3 N 5 0 0 1 0 0 0 0 1 1 3 N 6 0 0 1 0 0 0 0 0 1 N 7 0 0 0 0 0 1 1 2 N 8 1 1 0 0 0 0 0 2 N 9 0 0 0 1 0 0 0 0 1 N a 0 0 0 1 0 0 0 0 1 N b 0 0 0 1 1 0 0 0 3 N c 0 0 1 0 0 0 2 N 1 0 0 0 0 N 2 0 0 0 0 N 3 0 0 0 0 N 4 0 0 0 0 N 5 0 0 0 0 N 6 0 0 0 0 N 7 0 0 0 0 N 8 0 0 0 0 N 9 0 0 0 0 N a 0 0 0 0 N b 0 0 0 0 N c 0 0 0 0

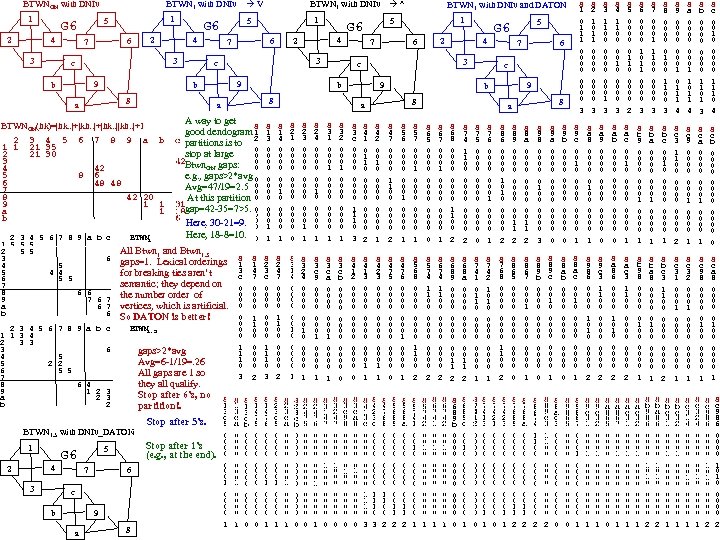BTWNGN with DNIv 1 1 5 G 6 4 2 BTWN 1 with DNIv BTWNGN with DNIv 1 1 5 G 6 4 2 BTWN 1 with DNIv V 3 4 3 c 9 b 2 1 1 2 3 4 5 6 7 8 9 a b 3 4 5 21 30 6 7 8 9 8 a b 42 6 48 48 42 20 1 1 1 2 3 4 5 6 7 8 9 a b c 1 5 5 5 2 5 5 3 6 4 5 5 4 4 6 5 5 7 8 6 6 9 7 6 7 a 6 7 b 6 2 3 4 5 6 7 8 9 a b c 1 1 3 4 2 3 3 3 6 4 5 5 2 2 6 5 5 7 8 6 4 9 1 2 3 a 2 3 b 2 BTWN 1 S 1 3 0 0 0 1 1 All Btwn 1 and Btwn 1. 5 gaps=1. Lexical orderings for breaking ties aren’t semantic; they depend on the number order of vertices, which is artificial. So DATON is better! BTWN 1. 5 gaps>2*avg Avg=6 -1/19=. 26 All gaps are 1 so they all qualify. Stop after 6’s, no partition!. Stop after 5’s. BTWN 1. 5 with DNIv_DATON 1 4 2 3 Stop after 1’s (e. g. , at the end). 5 G 6 6 7 c 9 b a 8 S 1 3 c 9 0 0 0 0 1 S 1 3 c 0 0 0 0 1 1 1 0 3 S 1 3 c a 0 0 0 0 1 S 1 4 7 0 0 1 1 0 0 0 2 S 1 3 c b 0 0 0 0 S 1 4 7 5 0 0 0 0 8 S 2 3 c 9 0 0 0 0 1 S 3 1 1 0 0 0 0 0 1 3 S 4 1 1 0 0 0 0 0 3 S 5 0 0 0 1 1 0 0 0 2 S 6 0 0 1 0 1 1 0 0 3 S 7 0 0 0 1 1 1 0 0 0 3 S 8 0 0 0 1 1 0 0 3 S 9 0 0 0 0 1 1 1 4 S a 0 0 0 0 1 1 4 S b 0 0 0 0 1 1 0 1 3 S c 0 0 1 0 0 0 1 1 1 0 4 S 2 3 c a 0 0 0 0 1 S 2 3 0 0 0 1 1 S 2 4 0 0 0 1 S 3 1 0 0 0 1 S 3 2 0 0 0 1 0 0 0 0 1 S 3 c 0 0 0 0 1 1 1 0 3 S 4 1 0 1 1 0 0 0 0 0 2 S 4 2 0 0 1 0 0 0 0 0 1 S 4 7 0 0 1 1 0 0 0 2 S 5 6 0 0 0 0 1 S 5 7 0 0 0 1 0 0 0 0 1 S 6 5 0 0 0 0 S 6 7 0 0 0 1 0 0 0 0 1 S 6 8 0 0 0 0 1 1 0 0 2 S 7 4 1 1 0 0 0 0 0 2 S 7 5 0 0 0 0 S 7 6 0 0 0 0 1 S 8 6 0 0 1 0 0 0 2 S 8 9 0 0 0 0 0 1 1 2 S 8 a 0 0 0 0 0 1 1 2 S 9 8 0 0 0 1 0 0 0 3 S 9 a 0 0 0 0 S 9 b 0 0 0 0 S 9 c 0 0 1 0 0 0 0 0 1 S a 8 0 0 0 1 S a 9 0 0 0 0 S a b 0 0 0 0 S a c 0 0 1 0 0 0 0 0 1 S b 9 0 0 0 0 1 S b a 0 0 0 0 1 S b c 0 0 1 0 0 0 0 0 1 S c 3 1 1 0 0 0 0 0 2 S c 9 0 0 0 0 1 S c a 0 0 0 0 1 S c b 0 0 0 0 S 3 1 4 0 0 0 1 S 2 4 7 0 0 1 1 0 0 0 2 S 1 4 7 6 0 0 0 0 1 8 a S 2 1 0 1 1 0 0 0 0 3 S 2 1 0 0 0 0 S 1 4 0 0 0 1 S 2 3 c 0 0 0 0 1 1 1 0 3 9 b a 6 7 c 9 8 A way to get S good dendogram 1 c partitions is to 2 0 stop at large 0 42 Btwn gaps: 0 GN 0 e. g. , gaps>2*avg 0 Avg=47/19=2. 5 0 0 At this partition 0 31 18 gap=42 -35=7>5. 0 0 6 Here, 30 -21=9. 0 0 Here, 18 -8=10. 0 4 3 b 5 G 6 2 6 c 9 a 1 7 3 c 8 BTWNGN(hk)=|hk. . |+|kh. . |+|hk. . ||kh. . |+1 4 S 1 0 1 1 1 0 0 0 0 3 BTWN 1 with DNIv and DATON 5 G 6 2 6 7 b a 1 5 G 6 2 6 7 BTWN 1 with DNIv ^ S 3 2 4 0 0 0 1 S 3 c 9 0 0 0 0 1 S 3 c a 0 0 0 0 1 S 3 c b 0 0 0 0 S 4 1 2 0 0 0 0 S 4 1 3 0 0 0 1 1 S 4 2 3 0 0 0 1 1 S 4 7 5 0 0 0 0 S 4 7 6 0 0 0 0 1 S 5 6 8 0 0 0 0 1 1 0 0 2 S 5 7 4 1 1 0 0 0 0 0 2 S 6 8 9 0 0 0 0 0 1 1 2 S 6 8 a 0 0 0 0 0 1 1 2 S 7 4 1 0 1 1 0 0 0 0 0 1 S 7 4 2 1 0 0 0 0 0 1 S 7 6 8 0 0 0 0 1 1 0 0 2 S 8 6 5 0 0 0 0 S 8 6 7 0 0 0 1 0 0 0 0 1 S 8 9 b 0 0 0 0 S 8 9 c 0 0 1 0 0 0 0 0 1 S 8 a b 0 0 0 0 S 8 a c 0 0 1 0 0 0 0 0 1 S 9 8 6 0 0 1 0 0 0 2 S 9 c 3 1 1 0 0 0 0 0 2 S a 8 6 0 0 1 0 0 0 2 S a c 3 1 1 0 0 0 0 0 2 S b 9 8 0 0 0 1 S b a 8 0 0 0 1 S b c 3 1 1 0 0 0 0 0 2 S c 3 1 0 0 0 1 S c 3 2 0 0 0 1 0 0 0 0 1 S c 9 8 0 0 0 1 S c a 8 0 0 0 1 S 2 4 7 5 0 0 0 0 S 2 4 7 6 0 0 0 0 1 S 3 c a 8 0 0 0 1 0 0 0 0 S 4 1 3 c 0 0 0 0 1 1 1 0 3 S 5 6 8 a 0 0 0 0 0 1 1 2 S 5 7 4 1 0 0 0 1 S 6 8 9 b 0 0 0 0 S 6 8 9 c 0 0 1 0 0 0 0 0 1 S 7 4 1 2 0 0 0 0 S 7 6 8 9 0 0 0 0 0 1 1 2 S 7 6 8 a 0 0 0 0 0 1 1 2 S 9 8 6 7 0 0 0 1 0 0 0 0 1 S 9 c 3 1 0 0 0 0 0 0 0 0 1 S a c 3 2 0 0 0 1 0 0 0 0 1 S b c 3 2 0 0 0 1 0 0 0 0 1 S c 3 1 4 0 0 0 1 S 2 3 c b 0 0 0 0 S 3 1 4 7 0 0 1 0 0 0 0 S 3 2 4 7 0 0 1 0 0 0 0 S 3 c 9 8 0 0 0 1 0 0 0 0 S 4 2 3 c 0 0 0 0 1 1 1 0 3 S 4 7 6 8 0 0 0 0 1 1 0 0 2 S 5 6 8 9 0 0 0 0 0 1 1 2 S 5 7 4 2 0 0 1 0 0 0 0 0 1 S 6 7 4 1 0 0 0 1 S 6 7 4 2 0 0 1 0 0 0 0 0 1 S 7 4 1 3 0 0 0 1 1 S 7 4 2 1 0 0 0 0 S 7 4 2 3 0 0 0 1 1 S 8 6 7 4 1 1 0 0 0 0 0 2 S 8 9 c 3 1 1 0 0 0 0 0 2 S 8 a c 3 0 0 0 0 S 9 8 6 5 0 0 0 0 S 9 c 3 2 0 0 0 1 0 0 0 0 1 S a 8 6 5 0 0 0 0 S a 8 6 7 0 0 0 1 0 0 0 0 1 S b 9 8 6 0 0 1 0 0 0 2 S b a 8 6 0 0 1 0 0 0 2 S b c 3 1 0 0 0 1 S c 3 2 4 0 0 0 1 S c 9 8 6 0 0 0 0 1 0 1 0 0 0 0 0 2

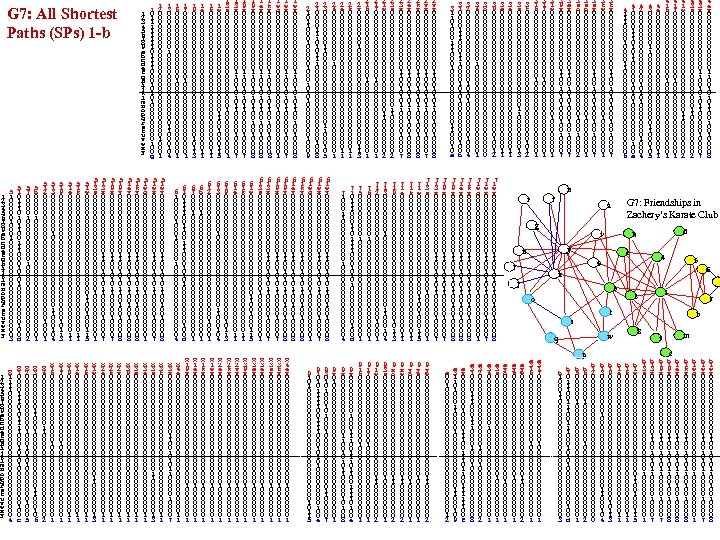1 2 3 4 5 6 7 8 9 a b c d e 1 2 3 4 5 6 7 8 9 a b c d e f g h i j k l m n o p q r s t u v w x y G 7: All Shortest Paths (SPs) 1 -b 1 2 3 4 5 6 7 8 9 a b c d e f g h i j k l m n o p q r s t u v w x y 5 1 0 0 0 0 0 0 0 0 3 8 1 1 0 0 0 0 0 0 0 0 4 5 1 0 1 1 0 0 1 1 1 0 0 0 1 0 1 0 0 0 0 0 1 0 0 d 8 1 0 0 1 1 1 0 0 0 1 0 1 0 0 0 0 0 1 0 0 c 5 7 0 0 0 0 0 1 0 0 0 0 0 0 2 8 2 0 0 0 0 1 0 0 0 1 0 1 0 0 0 5 5 b 0 0 0 1 0 0 0 0 0 0 0 1 8 3 0 0 0 0 1 1 0 0 0 0 1 1 0 0 0 1 0 6 1 0 1 1 1 1 0 0 0 1 0 1 0 0 0 0 0 1 0 0 g 1 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 5 1 3 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 1 0 4 5 1 9 0 0 0 0 0 0 0 0 1 0 1 1 3 5 1 e 0 0 0 0 0 0 0 0 0 1 1 5 1 k 0 0 0 0 0 0 0 0 0 1 1 5 1 w 0 0 0 0 0 0 1 1 0 0 0 1 1 5 5 1 3 s 0 0 0 0 0 0 1 0 0 0 0 0 1 5 1 3 x 0 0 0 0 0 0 0 1 1 0 0 1 0 1 0 1 1 0 0 0 0 0 1 0 0 0 0 7 5 1 9 y 0 0 0 0 1 1 0 0 1 0 0 8 5 1 e y 0 0 0 0 1 1 0 0 1 0 0 8 5 1 k y 0 0 0 0 1 1 0 0 1 0 0 8 5 1 w q 0 0 0 0 0 0 1 0 0 0 0 0 1 5 1 w x 0 0 0 0 1 1 0 0 1 0 1 1 0 0 0 1 0 0 7 5 1 w y 0 0 0 0 1 1 0 0 1 0 0 8 8 4 0 0 0 1 1 0 0 0 0 0 2 8 1 6 0 0 0 0 1 0 0 0 0 0 1 8 1 7 0 0 0 0 1 0 0 0 0 0 1 8 1 9 0 0 0 0 0 0 0 0 0 1 1 8 1 e 0 0 0 0 0 0 0 0 0 1 1 8 1 k 0 0 0 0 0 0 0 0 0 1 1 8 1 w 0 0 0 0 0 0 1 1 0 0 0 0 1 3 8 2 e 0 0 0 0 0 0 0 0 0 1 1 8 2 k 0 0 0 0 0 0 0 0 0 1 1 8 2 v 0 0 0 0 0 0 0 0 0 1 1 8 3 9 0 0 0 0 0 0 0 0 0 1 1 8 3 a 0 0 0 0 0 0 0 0 0 1 1 8 3 e 0 0 0 0 0 0 0 0 0 1 1 8 3 s 0 0 0 0 0 0 1 1 0 0 0 0 1 3 8 3 t 0 0 0 0 0 0 0 0 0 1 1 8 3 x 0 0 0 0 1 1 0 0 1 0 1 1 0 0 0 1 0 0 7 1 6 0 0 0 0 1 0 0 0 0 0 1 1 7 0 0 0 0 1 0 0 0 0 0 1 1 9 0 0 0 0 0 0 0 0 1 0 1 1 3 1 e 0 0 0 0 0 0 0 0 0 1 1 1 k 0 0 0 0 0 0 0 0 0 1 1 1 w 0 0 0 0 0 0 1 1 0 0 0 1 1 5 1 3 s 0 0 0 0 0 0 1 0 0 0 0 0 1 1 3 x 0 0 0 0 0 0 0 1 1 0 0 1 0 1 0 1 1 0 0 0 0 0 1 0 0 0 0 7 1 9 y 0 0 0 0 1 1 0 0 1 0 0 8 1 e y 0 0 0 0 1 1 0 0 1 0 0 8 1 k y 0 0 0 0 1 1 0 0 1 0 0 8 1 w q 0 0 0 0 0 0 1 0 0 0 0 0 1 1 w x 0 0 0 0 1 1 0 0 1 0 1 1 0 0 0 1 0 0 7 1 w y 0 0 0 0 1 1 0 0 1 0 0 8 6 1 0 0 0 0 0 0 0 0 0 0 4 1 3 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 1 0 4 6 1 0 1 1 0 0 1 1 1 0 0 0 1 0 1 0 0 0 0 0 1 0 0 d 6 7 0 0 1 0 0 0 0 0 0 0 0 1 6 b 0 0 1 0 0 0 0 0 0 0 0 1 6 1 2 0 0 0 0 0 0 0 0 1 0 0 0 1 6 1 3 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 1 0 4 6 1 9 0 0 0 0 0 0 0 0 1 0 1 1 3 6 1 e 0 0 0 0 0 0 0 0 0 1 1 6 1 k 0 0 0 0 0 0 0 0 0 1 1 6 1 w 0 0 0 0 0 0 1 1 0 0 0 1 1 5 6 1 3 s 0 0 0 0 0 0 1 0 0 0 0 0 1 6 1 3 x 0 0 0 0 0 0 0 1 1 0 0 1 0 1 0 1 1 0 0 0 0 0 1 0 0 0 0 7 6 1 9 y 0 0 0 0 1 1 0 0 1 0 0 8 6 1 e y 0 0 0 0 1 1 0 0 1 0 0 8 8 3 e y 0 0 0 0 0 0 0 1 0 0 0 0 1 8 3 s y 0 0 0 0 0 0 0 1 0 0 0 0 1 8 3 t y 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 1 8 4 e 0 0 0 0 0 0 0 0 0 1 1 8 1 9 y 0 0 0 0 0 0 0 1 0 0 0 0 1 8 1 e y 0 0 0 0 0 0 0 1 0 0 0 0 1 8 1 k y 0 0 0 0 0 0 0 1 0 0 0 0 1 8 1 w y 0 0 0 0 0 0 0 1 0 0 0 0 1 8 2 e y 0 0 0 0 0 0 0 1 0 0 0 0 1 8 2 k y 0 0 0 0 0 0 0 1 0 0 0 0 1 8 2 v y 0 0 0 0 0 0 0 1 0 0 0 0 1 8 3 9 y 0 0 0 0 0 0 0 1 0 0 0 0 1 8 3 a y 0 0 0 0 0 0 0 1 0 0 0 0 1 2 1 0 1 1 0 0 0 0 0 1 0 0 0 9 6 1 k y 0 0 0 0 1 1 0 0 1 0 0 8 2 1 0 0 1 1 1 0 0 0 0 0 1 0 0 8 2 3 0 0 0 0 1 1 0 0 0 0 0 1 1 0 0 0 1 0 5 6 1 w q 0 0 0 0 0 0 1 0 0 0 0 0 1 6 1 w x 0 0 0 0 1 1 0 0 1 0 1 1 0 0 0 1 0 0 7 6 1 w y 0 0 0 0 1 1 0 0 1 0 0 8 9 1 0 0 0 0 0 0 0 1 0 1 1 5 9 1 0 1 1 1 0 0 0 1 0 1 0 0 0 0 0 1 0 0 e 9 3 0 1 0 1 0 0 0 0 0 0 0 1 1 0 0 0 7 9 v 0 1 0 0 0 0 0 0 0 0 1 2 e 0 0 0 0 0 0 0 0 0 1 1 2 k 0 0 0 0 0 0 0 0 0 1 1 2 v 0 0 0 0 1 0 0 0 0 0 0 1 1 3 2 1 6 0 0 0 0 1 0 0 0 0 0 1 2 1 7 0 0 0 0 1 0 0 0 0 0 1 2 1 w 0 0 0 0 0 0 1 1 0 0 0 0 2 2 3 s 0 0 0 0 0 0 1 1 0 0 0 0 0 2 2 3 x 0 0 0 0 1 1 0 0 1 0 1 1 0 0 0 1 0 0 7 2 e y 0 0 0 0 1 1 0 0 1 0 0 8 2 k y 0 0 0 0 1 1 0 0 1 0 0 8 2 v x 0 0 0 0 1 1 0 0 1 0 1 1 0 0 0 1 0 0 7 2 v y 0 0 0 0 1 1 0 0 1 0 0 8 7 1 0 0 0 1 1 0 0 0 0 0 0 0 4 2 4 0 0 0 1 0 0 0 0 0 0 1 7 1 0 1 1 1 0 0 0 1 0 1 0 0 0 0 0 1 0 0 d 7 5 0 0 0 0 0 1 0 0 0 0 0 0 1 7 6 0 0 0 0 0 1 0 0 0 0 0 0 1 7 1 2 0 0 0 0 0 0 0 0 1 0 0 0 1 7 1 3 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 1 0 4 7 1 9 0 0 0 0 0 0 0 0 1 0 1 1 3 7 1 e 0 0 0 0 0 0 0 0 0 1 1 7 1 k 0 0 0 0 0 0 0 0 0 1 1 7 1 w 0 0 0 0 0 0 1 1 0 0 0 1 1 5 7 1 3 s 0 0 0 0 0 0 1 0 0 0 0 0 1 7 1 3 x 0 0 0 0 1 1 0 0 1 0 1 1 0 0 0 1 0 0 7 9 y 0 0 0 0 0 1 1 1 0 0 1 1 0 1 0 0 e 9 1 6 0 0 0 0 1 0 0 0 0 0 1 9 1 7 0 0 0 0 1 0 0 0 0 0 1 9 1 w 0 0 0 0 0 0 1 1 0 0 0 0 2 9 3 s 0 0 0 0 0 0 1 0 0 0 0 0 1 9 x o 0 0 0 0 0 0 1 1 0 0 0 0 2 9 x w 0 0 0 0 0 0 1 1 0 0 0 0 2 9 y o 0 0 0 0 0 0 0 1 0 0 0 0 1 9 y s 0 0 0 0 0 0 1 0 0 0 0 0 1 9 y w 0 0 0 0 0 0 1 1 0 0 0 0 2 9 x 0 0 0 0 1 1 0 0 1 0 1 1 0 0 0 1 0 0 8 3 1 1 0 0 0 1 1 1 0 0 0 0 1 1 0 0 0 1 0 a 7 1 9 x 0 0 0 0 1 1 0 0 1 0 1 1 0 0 0 1 0 0 7 a 0 0 1 0 0 0 0 0 0 0 0 1 2 3 1 0 0 1 1 1 0 0 0 0 1 0 1 0 0 0 0 0 1 0 0 b 3 2 0 0 0 0 0 1 0 1 0 0 0 4 3 4 0 0 0 1 0 0 0 0 0 0 1 3 8 0 0 0 0 0 0 0 0 0 3 9 0 0 0 0 0 0 0 0 1 0 0 1 2 7 1 9 y 0 0 0 0 1 1 0 0 1 0 0 8 7 1 e y 0 0 0 0 1 1 0 0 1 0 0 8 7 1 k y 0 0 0 0 1 1 0 0 1 0 0 8 7 1 w q 0 0 0 0 0 0 1 0 0 0 0 0 1 7 1 w x 0 0 0 0 1 1 0 0 1 0 1 1 0 0 0 1 0 0 7 7 1 w y 0 0 0 0 1 1 0 0 1 0 0 8 a y 0 0 0 0 1 1 1 0 0 1 1 1 0 0 f a 3 1 0 0 1 1 1 0 0 0 0 0 0 0 8 a 3 2 0 0 0 0 0 1 0 0 0 0 2 a 3 4 0 0 0 1 0 0 0 0 0 0 1 a 3 s 0 0 0 0 0 0 1 0 0 0 0 0 1 a 3 1 1 0 0 0 0 0 0 1 1 0 0 0 1 0 9 3 a 0 0 0 0 0 0 0 0 0 1 1 3 e 0 0 0 0 0 0 0 0 0 1 1 3 s 0 0 0 0 0 0 1 1 0 0 0 0 1 3 3 1 6 0 0 0 0 1 0 0 0 0 0 1 3 t 0 0 0 0 0 0 0 0 1 2 3 1 7 0 0 0 0 1 0 0 0 0 0 1 3 1 w 0 0 0 0 0 0 0 1 0 0 0 0 1 3 9 y 0 0 0 0 1 1 0 0 1 0 0 7 3 a y 0 0 0 0 1 1 0 0 1 0 0 7 3 s o 0 0 0 0 0 0 0 1 0 0 0 0 2 3 s p 0 0 0 0 0 0 0 1 0 0 0 0 1 3 s y 0 0 0 0 1 1 0 0 1 0 0 7 3 t w 0 0 0 0 0 0 0 1 0 0 0 0 1 3 t y 0 0 0 0 1 1 0 0 1 0 0 7 4 1 0 0 1 1 1 0 0 0 1 0 1 0 0 0 0 0 1 0 0 a 4 1 1 1 0 0 0 0 0 0 0 6 4 2 0 0 0 0 0 1 0 1 0 0 0 4 4 3 0 0 0 0 1 1 0 0 0 0 0 1 1 0 0 0 1 0 5 4 1 6 0 0 0 0 1 0 0 0 0 0 1 4 e 0 0 0 0 0 0 0 0 0 1 1 4 1 7 0 0 0 0 1 0 0 0 0 0 1 4 1 w 0 0 0 0 0 0 1 1 0 0 0 0 2 4 3 s 0 0 0 0 0 0 1 1 0 0 0 0 0 2 4 3 x 0 0 0 0 1 1 0 0 1 0 1 1 0 0 0 1 0 0 7 4 e y 0 0 0 0 1 1 0 0 1 0 0 8 n f r G 7: Friendships in Zachery’s Karate Club a g y u d k v e 4 9 l 5 6 x j 3 1 2 o 7 t b s a y o 0 0 0 0 0 0 0 1 0 0 0 0 1 a y s 0 0 0 0 0 0 1 0 0 0 0 0 1 a y w 0 0 0 0 0 0 1 1 0 0 0 0 2 a 3 1 6 0 0 0 0 1 0 0 0 0 0 1 a 3 1 7 0 0 0 0 1 0 0 0 0 0 1 8 w q p b 1 0 0 0 1 1 0 0 0 0 0 0 0 3 b 1 0 1 1 1 0 0 0 1 0 1 0 0 0 0 0 1 0 0 d b 5 0 0 0 1 0 0 0 0 0 0 0 1 b 6 0 0 0 1 0 0 0 0 0 2 b 1 2 0 0 0 0 0 0 0 0 0 b 1 3 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 1 0 4 b 1 9 0 0 0 0 0 0 0 0 1 0 1 1 3 b 1 e 0 0 0 0 0 0 0 0 0 1 1 b 1 k 0 0 0 0 0 0 0 0 0 1 1 b 1 w 0 0 0 0 0 0 1 1 0 0 0 1 1 5 m i b 1 3 s 0 0 0 0 0 0 1 0 0 0 0 0 1 b 1 3 x 0 0 0 0 1 1 0 0 1 0 1 1 0 0 0 1 0 0 7 b 1 9 x 0 0 0 0 1 1 0 0 1 0 1 1 0 0 0 1 0 0 7 c b 1 9 y 0 0 0 0 1 1 0 0 1 0 0 8 b 1 e y 0 0 0 0 1 1 0 0 1 0 0 8 b 1 k y 0 0 0 0 1 1 0 0 1 0 0 8 b 1 w q 0 0 0 0 0 0 1 0 0 0 0 0 1 b 1 w x 0 0 0 0 1 1 0 0 1 0 1 1 0 0 0 1 0 0 7 b 1 w y 0 0 0 0 1 1 0 0 1 0 0 8

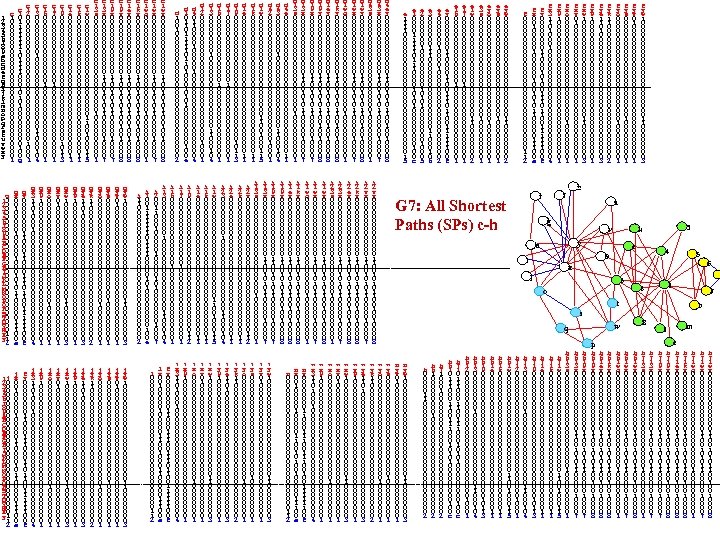1 2 3 4 5 6 7 8 9 a b c d e 1 2 3 4 5 6 7 8 9 a b c d e f g h i j k l m n o p q r s t u v w x y c 1 0 0 0 0 0 0 0 0 0 1 g 10 20 30 40 50 60 70 80 90 A 0 B 0 C 0 D 0 E 0 F 0 G 0 H 0 I 0 J 0 K 0 L 0 M 0 N 0 O 0 P 0 Q 0 R 0 S 0 T 0 U 0 V 0 W 0 X 1 y 1 2 1 j 20 30 40 50 60 70 80 90 A 0 B 0 C 0 D 0 E 0 F 0 G 0 H 0 I 0 J 0 K 0 L 0 M 0 N 0 O 0 P 0 Q 0 R 0 S 0 T 0 U 0 V 0 W 0 X 0 y 1 1 2 c 1 0 1 1 1 1 0 0 0 1 0 1 0 0 0 0 0 1 0 0 g g x 0 0 1 0 0 0 0 0 1 0 1 0 1 1 0 0 0 1 1 1 0 0 a j x 0 0 1 0 0 0 0 0 1 1 0 0 1 0 1 1 0 0 0 1 1 1 0 0 a c 1 2 0 0 0 0 0 0 0 0 1 0 0 0 1 g y 0 0 0 0 1 1 1 0 0 1 1 1 0 0 f f y 0 0 0 0 1 1 0 1 1 0 0 1 1 1 0 0 f c 1 3 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 1 0 4 g x 3 1 1 0 0 0 0 0 0 0 0 4 j x 3 1 1 0 0 0 0 0 0 0 0 4 c 1 6 0 0 0 0 1 0 0 0 0 0 1 g x 9 1 0 0 0 0 0 0 0 0 0 1 j x 9 1 0 0 0 0 0 0 0 0 0 1 c 1 7 0 0 0 0 1 0 0 0 0 0 1 g x o 0 0 0 0 0 0 0 1 0 0 0 0 1 j x o 0 0 0 0 0 0 0 1 0 0 0 0 1 c 1 9 0 0 0 0 0 0 0 0 1 0 1 1 3 g x v 0 1 0 0 0 0 0 0 0 0 1 j x v 0 1 0 0 0 0 0 0 0 0 1 c 1 e 0 0 0 0 0 0 0 0 0 1 1 g x w 1 0 0 0 0 0 0 1 1 0 0 0 0 3 j x w 1 0 0 0 0 0 0 1 1 0 0 0 0 3 c 1 k 0 0 0 0 0 0 0 0 0 1 1 g y 9 1 0 0 0 0 0 0 0 0 0 1 j y 9 1 0 0 0 0 0 0 0 0 0 1 c 1 w 0 0 0 0 0 0 1 1 0 0 0 1 1 5 g y e 1 1 0 0 0 0 0 0 0 0 3 j y e 1 1 0 0 0 0 0 0 0 0 3 c 1 3 s 0 0 0 0 0 0 1 0 0 0 0 0 1 g y k 1 1 0 0 0 0 0 0 0 0 2 j y k 1 1 0 0 0 0 0 0 0 0 2 c 1 3 x 0 0 0 0 1 1 0 0 1 0 1 1 0 0 0 1 0 0 7 g y o 0 0 0 0 0 0 0 1 0 0 0 0 1 j y o 0 0 0 0 0 0 0 1 0 0 0 0 1 c 1 9 x 0 0 0 0 1 1 0 0 1 0 1 1 0 0 0 1 0 0 7 g y s 0 0 0 0 0 0 1 0 0 0 0 0 1 j y s 0 0 0 0 0 0 1 0 0 0 0 0 1 c 1 9 y 0 0 0 0 1 1 0 0 1 0 0 8 g y v 0 1 0 0 0 0 0 0 0 0 1 j y v 0 1 0 0 0 0 0 0 0 0 1 c 1 e y 0 0 0 0 1 1 0 0 1 0 0 8 g y w 1 0 0 0 0 0 0 1 1 0 0 0 0 3 j y w 1 0 0 0 0 0 0 1 1 0 0 0 0 3 c 1 k y 0 0 0 0 1 1 0 0 1 0 0 8 c 1 w q 0 0 0 0 0 0 1 0 0 0 0 0 1 c 1 w x 0 0 0 0 1 1 0 0 1 0 1 1 0 0 0 1 0 0 7 c 1 w y 0 0 0 0 1 1 0 0 1 0 0 8 i 1 1 0 0 0 0 0 0 0 0 2 i 1 0 0 1 1 1 1 0 0 0 1 0 0 0 0 0 1 0 0 e i 2 0 0 1 1 0 0 0 0 0 1 0 0 0 0 1 0 0 0 7 i 1 3 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 1 0 4 l 0 0 0 0 0 0 0 0 1 1 2 l x 0 0 1 0 0 0 0 0 1 1 0 0 0 1 1 1 0 0 a d 1 0 0 0 0 0 0 0 0 2 i 1 6 0 0 0 0 1 0 0 0 0 0 1 f y 0 0 0 0 1 1 1 0 1 1 0 0 1 1 1 0 0 f i 1 7 0 0 0 0 1 0 0 0 0 0 1 l x 3 1 1 0 0 0 0 0 0 0 0 4 d 1 0 1 1 0 0 0 1 0 1 0 0 0 0 0 1 0 0 e i 1 9 0 0 0 0 0 0 0 0 1 1 2 l x 9 1 0 0 0 0 0 0 0 0 0 1 d 4 0 1 1 0 0 0 0 0 0 0 0 0 0 4 i 1 e 0 0 0 0 0 0 0 0 0 1 1 l x o 0 0 0 0 0 0 0 1 0 0 0 0 1 d 1 2 0 0 0 0 0 0 0 0 1 0 0 0 1 i 1 k 0 0 0 0 0 0 0 0 0 1 1 l x v 0 1 0 0 0 0 0 0 0 0 1 d 1 3 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 1 0 4 i 1 w 0 0 0 0 0 0 1 1 0 0 0 1 1 5 l x w 1 0 0 0 0 0 0 1 1 0 0 0 0 3 d 1 6 0 0 0 0 1 0 0 0 0 0 1 i 2 3 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 1 0 4 l y 9 1 0 0 0 0 0 0 0 0 0 1 d 1 7 0 0 0 0 1 0 0 0 0 0 1 i 2 e 0 0 0 0 0 0 0 0 0 1 1 l y e 1 1 0 0 0 0 0 0 0 0 3 d 1 9 0 0 0 0 0 0 0 0 1 0 1 1 3 i 2 k 0 0 0 0 0 0 0 0 0 1 1 l y k 1 1 0 0 0 0 0 0 0 0 2 d 1 e 0 0 0 0 0 0 0 0 0 1 1 i 2 v 0 0 0 0 0 0 0 0 1 1 2 l y o 0 0 0 0 0 0 0 1 0 0 0 0 1 d 1 k 0 0 0 0 0 0 0 0 0 1 1 i 1 3 s 0 0 0 0 0 0 1 0 0 0 0 0 1 l y s 0 0 0 0 0 0 1 0 0 0 0 0 1 d 1 w 0 0 0 0 0 0 1 1 0 0 0 1 1 5 i 1 3 x 0 0 0 0 1 1 0 0 1 0 1 1 0 0 0 1 0 0 7 l y v 0 1 0 0 0 0 0 0 0 0 1 d 4 2 0 0 0 0 0 0 0 0 1 0 0 0 1 i 1 9 x 0 0 0 0 1 1 0 0 1 0 1 1 0 0 0 1 0 0 7 l y w 1 0 0 0 0 0 0 1 1 0 0 0 0 3 d 4 3 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 1 0 4 i 1 9 y 0 0 0 0 1 1 0 0 1 0 0 8 d 4 e 0 0 0 0 0 0 0 0 0 1 1 i 1 e y 0 0 0 0 1 1 0 0 1 0 0 8 n 0 0 0 0 0 0 0 0 1 1 2 d 1 3 s 0 0 0 0 0 0 1 0 0 0 0 0 1 i 1 k y 0 0 0 0 1 1 0 0 1 0 0 8 n x 0 0 1 0 0 0 0 0 1 1 0 0 0 1 1 1 0 0 a d 1 3 x 0 0 0 0 1 1 0 0 1 0 1 1 0 0 0 1 0 0 7 i 1 w q 0 0 0 0 0 0 1 0 0 0 0 0 1 n y 0 0 0 0 1 1 1 0 0 1 1 1 1 0 0 f d 1 9 x 0 0 0 0 1 1 0 0 1 0 1 1 0 0 0 1 0 0 7 i 1 w x 0 0 0 0 1 1 0 0 1 0 1 1 0 0 0 1 0 0 7 n x 3 1 1 0 0 0 0 0 0 0 0 4 d 1 9 y 0 0 0 0 1 1 0 0 1 0 0 8 i 1 w y 0 0 0 0 1 1 0 0 1 0 0 8 n x 9 1 0 0 0 0 0 0 0 0 0 1 d 1 e y 0 0 0 0 1 1 0 0 1 0 0 8 i 2 3 s 0 0 0 0 0 0 1 0 0 0 0 0 1 n x o 0 0 0 0 0 0 0 1 0 0 0 0 1 d 1 k y 0 0 0 0 1 1 0 0 1 0 0 8 i 2 3 x 0 0 0 0 1 1 0 0 1 0 1 1 0 0 0 1 0 0 7 n x v 0 1 0 0 0 0 0 0 0 0 1 d 1 w q 0 0 0 0 0 0 1 0 0 0 0 0 1 i 2 e y 0 0 0 0 1 1 0 0 1 0 0 8 n x w 1 0 0 0 0 0 0 1 1 0 0 0 0 3 d 1 w x 0 0 0 0 1 1 0 0 1 0 1 1 0 0 0 1 0 0 7 i 2 k y 0 0 0 0 1 1 0 0 1 0 0 8 n y 9 1 0 0 0 0 0 0 0 0 0 1 d 1 w y 0 0 0 0 1 1 0 0 1 0 0 8 i 2 v x 0 0 0 0 1 1 0 0 1 0 1 1 0 0 0 1 0 0 7 n y e 1 1 0 0 0 0 0 0 0 0 3 d 4 3 s 0 0 0 0 0 0 1 0 0 0 0 0 1 d 4 3 x 0 0 0 0 1 1 0 0 1 0 1 1 0 0 0 1 0 0 7 d 4 e y 0 0 0 0 1 1 0 0 1 0 0 8 i 2 v y 0 0 0 0 1 1 0 0 1 0 0 8 n y k 1 1 0 0 0 0 0 0 0 0 2 e 1 1 0 0 0 0 0 0 0 0 1 5 e 1 0 0 1 1 1 0 0 1 0 1 0 0 0 0 0 1 0 0 c e 2 0 0 0 0 1 0 1 0 0 0 0 1 0 0 0 5 e 3 0 0 0 0 1 1 1 0 0 0 0 0 1 1 0 0 0 1 0 6 e 4 0 0 0 0 1 0 0 0 0 0 0 2 e y 0 0 0 0 1 1 0 0 1 1 1 0 0 f e 1 6 0 0 0 0 1 0 0 0 0 0 1 e 1 7 0 0 0 0 1 0 0 0 0 0 1 e 1 w 0 0 0 0 0 0 1 1 0 0 0 0 2 e 3 s 0 0 0 0 0 0 1 0 0 0 0 0 1 e y o 0 0 0 0 0 0 0 1 0 0 0 0 1 e y s 0 0 0 0 0 0 1 0 0 0 0 0 1 e y w 0 0 0 0 0 0 1 1 0 0 0 0 2 f 0 0 0 0 0 0 0 0 1 1 2 f x 0 0 1 0 0 0 1 0 1 1 0 0 0 1 1 1 0 0 a f x 3 1 1 0 0 0 0 0 0 0 0 4 f y 0 0 0 0 1 1 0 0 0 1 1 1 0 0 1 1 1 0 0 f f x 9 1 0 0 0 0 0 0 0 0 0 1 f x v 0 1 0 0 0 0 0 0 0 0 1 f x w 1 0 0 0 0 0 0 1 1 0 0 0 0 3 f y 9 1 0 0 0 0 0 0 0 0 0 1 f y e 1 1 0 0 0 0 0 0 0 0 3 f y k 1 1 0 0 0 0 0 0 0 0 2 f y o 0 0 0 0 0 0 0 1 0 0 0 0 1 f y s 0 0 0 0 0 0 1 0 0 0 0 0 1 f y v 0 1 0 0 0 0 0 0 0 0 1 f y w 1 0 0 0 0 0 0 1 1 0 0 0 0 3 n f r G 7: All Shortest Paths (SPs) c-h f x o 0 0 0 0 0 0 0 1 0 0 0 0 1 a g y u d k v e 4 9 l 5 j 3 1 2 o 7 t b s 8 w q m i c p n y o 0 0 0 0 0 0 0 1 0 0 0 0 1 n y s 0 0 0 0 0 0 1 0 0 0 0 0 1 n y v 0 1 0 0 0 0 0 0 0 0 1 n y w 1 0 0 0 0 0 0 1 1 0 0 0 0 3 h 0 0 0 1 1 0 0 0 0 0 0 0 2 h 6 1 0 0 0 0 0 0 0 0 2 h 7 1 0 0 0 0 0 0 0 0 2 h 6 1 0 1 1 1 0 0 0 1 0 1 0 0 0 0 0 1 0 0 c h 7 1 0 1 1 1 0 0 0 1 0 1 0 0 0 0 0 1 0 0 c h 6 1 2 0 0 0 0 0 0 0 0 1 0 0 0 1 h 6 1 3 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 1 0 4 h 6 1 9 0 0 0 0 0 0 0 0 1 0 1 1 3 h 6 1 e 0 0 0 0 0 0 0 0 0 1 1 h 6 1 k 0 0 0 0 0 0 0 0 0 1 1 h 6 1 w 0 0 0 0 0 0 1 1 0 0 0 1 1 5 h 7 1 2 0 0 0 0 0 0 0 0 1 0 0 0 1 h 7 1 3 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 1 0 4 6 x h 7 1 9 0 0 0 0 0 0 0 0 1 0 1 1 3 h 7 1 e 0 0 0 0 0 0 0 0 0 1 1 h 7 1 k 0 0 0 0 0 0 0 0 0 1 1 h 7 1 w 0 0 0 0 0 0 1 1 0 0 0 1 1 5 h 6 1 3 s 0 0 0 0 0 0 1 0 0 0 0 0 1 h 6 1 3 x 0 0 0 0 0 0 0 1 1 0 0 1 0 1 0 1 1 0 0 0 0 0 1 0 0 0 0 7 h 6 1 9 y 0 0 0 0 1 1 0 0 1 0 0 8 h 6 1 e y 0 0 0 0 1 1 0 0 1 0 0 8 h 6 1 k y 0 0 0 0 1 1 0 0 1 0 0 8 h 6 1 w q 0 0 0 0 0 0 1 0 0 0 0 0 1 h 6 1 w x 0 0 0 0 1 1 0 0 1 0 1 1 0 0 0 1 0 0 7 h 6 1 w y 0 0 0 0 1 1 0 0 1 0 0 8 h 7 1 3 s 0 0 0 0 0 0 1 0 0 0 0 0 1 h 7 1 3 x 0 0 0 0 0 0 0 1 1 0 0 1 0 1 0 1 1 0 0 0 0 0 1 0 0 0 0 7 h 7 1 9 y 0 0 0 0 1 1 0 0 1 0 0 8 h 7 1 e y 0 0 0 0 1 1 0 0 1 0 0 8 h 7 1 k y 0 0 0 0 1 1 0 0 1 0 0 8 h 7 1 w q 0 0 0 0 0 0 1 0 0 0 0 0 1 h 7 1 w x 0 0 0 0 1 1 0 0 1 0 1 1 0 0 0 1 0 0 7 h 7 1 w y 0 0 0 0 1 1 0 0 1 0 0 8

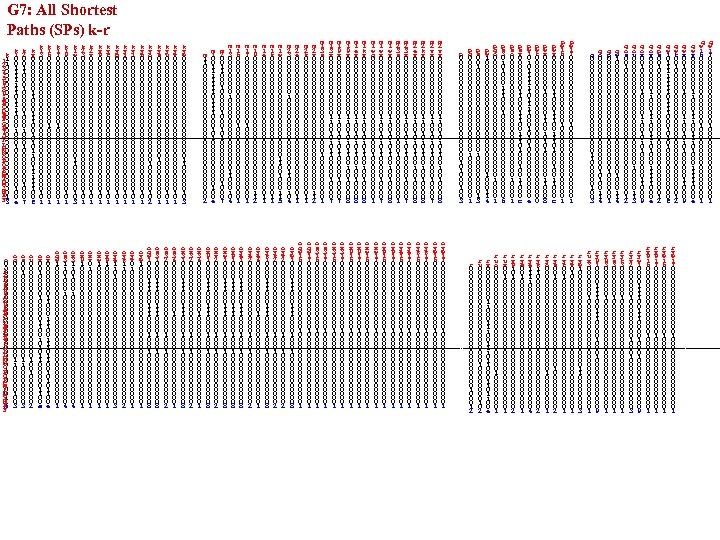G 7: All Shortest Paths (SPs) k-r k 11 21 30 40 50 60 G 7: All Shortest Paths (SPs) k-r k 11 21 30 40 50 60 70 80 90 A 0 B 0 C 0 D 0 E 0 F 0 G 0 H 0 I 0 J 0 K 0 L 0 M 0 N 0 O 0 P 0 Q 0 R 0 S 0 T 0 U 0 V 0 W 0 X 0 y 1 3 k 1 0 0 1 1 1 1 0 0 0 1 0 0 0 0 0 1 0 0 e k 2 0 0 1 1 0 0 0 0 0 1 0 0 0 0 1 0 0 0 7 k y 0 0 0 0 1 1 1 0 0 1 0 1 1 0 0 1 1 1 0 0 f k 1 3 0 0 0 0 0 0 0 0 1 0 1 k 1 6 0 0 0 0 1 0 0 0 0 0 1 k 1 7 0 0 0 0 1 0 0 0 0 0 1 k 1 9 0 0 0 0 0 0 0 0 1 0 1 k 1 w 0 0 0 0 0 0 1 1 0 0 0 1 0 3 k 2 3 0 0 0 0 0 0 0 0 1 0 1 k 2 v 0 0 0 0 0 0 0 0 1 0 1 k y 9 0 0 0 0 0 0 0 0 1 0 1 k y f 0 0 0 0 0 0 0 0 1 0 1 k y g 0 0 0 0 0 0 0 0 1 0 1 k y j 0 0 0 0 0 0 0 0 1 0 1 k y l 0 0 0 0 0 0 0 0 1 0 1 k y n 0 0 0 0 0 0 0 0 1 0 1 k y o 0 0 0 0 0 0 0 1 0 0 0 1 0 2 k y s 0 0 0 0 0 0 1 0 0 0 0 0 1 k y u 0 0 0 0 0 0 0 0 1 0 1 k y v 0 0 0 0 0 0 0 0 1 0 1 k y w 0 0 0 0 0 0 1 1 0 0 0 1 0 3 o 0 0 1 0 2 0 3 0 4 0 5 0 6 0 7 0 8 0 9 0 A 0 B 0 C 0 D 0 E 0 F 0 G 0 H 0 I 0 J 0 K 0 L 0 M 0 N 0 O 1 P 0 Q 1 R 0 S 1 T 0 U 0 V 1 W 1 X 5 y o q 0 0 0 0 0 0 1 1 0 0 0 1 0 0 3 o s 0 0 1 0 0 0 0 0 1 1 0 0 0 0 0 3 o u 0 0 0 0 0 0 1 0 0 0 0 2 o x 0 0 1 0 0 0 0 0 1 1 0 0 1 0 1 1 0 0 a o y 0 0 0 0 1 1 1 0 1 1 0 0 e o q w 1 0 0 0 0 0 0 0 0 0 1 o s 3 1 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 4 o x 9 1 0 0 0 0 0 0 0 0 0 1 o x v 0 1 0 0 0 0 0 0 0 0 1 o x w 1 0 0 0 0 0 0 0 0 0 1 o y 9 1 0 0 0 0 0 0 0 0 0 1 o y e 1 1 0 0 0 0 0 0 0 0 3 o y k 1 1 0 0 0 0 0 0 0 0 2 o y v 0 1 0 0 0 0 0 0 0 0 1 o y w 1 0 0 0 0 0 0 0 0 0 1 o q w 1 0 0 0 0 1 1 1 0 0 0 0 1 0 0 0 0 0 0 8 o s 3 2 0 0 0 0 0 1 0 0 0 0 2 o s 3 4 0 0 0 1 0 0 0 0 0 0 1 o x 3 1 0 0 1 1 1 0 0 0 0 0 0 0 8 m 1 1 0 0 0 0 0 0 0 0 2 o x 3 2 0 0 0 0 0 1 0 0 0 0 2 o x 3 4 0 0 0 1 0 0 0 0 0 0 1 o x 9 1 0 0 1 1 1 0 0 0 0 0 0 0 8 m 1 0 0 1 1 1 1 0 0 0 1 0 0 0 1 0 0 e o x v 2 0 0 0 0 0 1 0 0 0 0 2 m 2 0 0 1 1 0 0 0 0 0 1 0 0 0 7 o x w 1 0 0 1 1 1 0 0 0 0 0 0 0 8 m 1 3 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 1 0 4 o y 9 1 0 0 1 1 1 0 0 0 0 0 0 0 8 m 1 6 0 0 0 0 1 0 0 0 0 0 1 o y e 1 0 0 1 1 1 0 0 0 0 0 0 0 8 m 1 7 0 0 0 0 1 0 0 0 0 0 1 o y e 2 0 0 0 0 0 1 0 0 0 0 2 m 1 9 0 0 0 0 0 0 0 0 1 1 2 o y e 4 0 0 0 1 0 0 0 0 0 0 1 m 1 e 0 0 0 0 0 0 0 0 0 1 1 o y k 1 0 0 1 1 1 0 0 0 0 0 0 0 8 m 1 k 0 0 0 0 0 0 0 0 0 1 1 o y k 2 0 0 0 0 0 1 0 0 0 0 2 m 1 w 0 0 0 0 0 0 1 1 0 0 0 1 1 5 o y v 2 0 0 0 0 0 1 0 0 0 0 2 m 2 3 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 1 0 4 o y w 1 0 0 1 1 1 0 0 0 0 0 0 0 8 m 2 e 0 0 0 0 0 0 0 0 0 1 1 o q w 1 6 0 0 0 0 1 0 0 0 0 0 1 m 2 k 0 0 0 0 0 0 0 0 0 1 1 o q w 1 7 0 0 0 0 1 0 0 0 0 0 1 m 2 v 0 0 0 0 0 0 0 0 1 1 2 o s 3 1 6 0 0 0 0 1 0 0 0 0 0 1 m 1 3 s 0 0 0 0 0 0 1 0 0 0 0 0 1 o s 3 1 7 0 0 0 0 1 0 0 0 0 0 1 m 1 3 x 0 0 0 0 1 1 0 0 1 0 1 1 0 0 0 1 0 0 7 o x 3 1 6 0 0 0 0 1 0 0 0 0 0 1 m 1 9 x 0 0 0 0 1 1 0 0 1 0 1 1 0 0 0 1 0 0 7 o x 3 1 7 0 0 0 0 1 0 0 0 0 0 1 m 1 9 y 0 0 0 0 1 1 0 0 1 0 0 8 o x 9 1 6 0 0 0 0 1 0 0 0 0 0 1 m 1 e y 0 0 0 0 1 1 0 0 1 0 0 8 o x 9 1 7 0 0 0 0 1 0 0 0 0 0 1 m 1 k y 0 0 0 0 1 1 0 0 1 0 0 8 o x w 1 6 0 0 0 0 1 0 0 0 0 0 1 m 1 w q 0 0 0 0 0 0 1 0 0 0 0 0 1 o x w 1 7 0 0 0 0 1 0 0 0 0 0 1 m 1 w x 0 0 0 0 1 1 0 0 1 0 1 1 0 0 0 1 0 0 7 o y 9 1 6 0 0 0 0 1 0 0 0 0 0 1 m 1 w y 0 0 0 0 1 1 0 0 1 0 0 8 o y 9 1 7 0 0 0 0 1 0 0 0 0 0 1 m 2 3 s 0 0 0 0 0 0 1 0 0 0 0 0 1 o y e 1 6 0 0 0 0 1 0 0 0 0 0 1 m 2 3 x 0 0 0 0 1 1 0 0 1 0 1 1 0 0 0 1 0 0 7 o y e 1 7 0 0 0 0 1 0 0 0 0 0 1 m 2 e y 0 0 0 0 1 1 0 0 1 0 0 8 o y k 1 6 0 0 0 0 1 0 0 0 0 0 1 m 2 k y 0 0 0 0 1 1 0 0 1 0 0 8 o y k 1 7 0 0 0 0 1 0 0 0 0 0 1 m 2 v x 0 0 0 0 1 1 0 0 1 0 1 1 0 0 0 1 0 0 7 o y w 1 6 0 0 0 0 1 0 0 0 0 0 1 m 2 v y 0 0 0 0 1 1 0 0 1 0 0 8 o y w 1 7 0 0 0 0 1 0 0 0 0 0 1 p 0 0 0 0 0 0 0 1 0 0 3 p q 0 0 0 0 0 0 1 0 0 0 0 0 1 p s 0 0 1 0 0 0 0 0 1 0 0 0 0 0 1 3 p w 1 0 0 0 0 0 0 0 1 0 0 0 1 1 4 p q o 0 0 0 0 0 0 0 0 1 0 0 1 p s 3 0 1 0 0 0 1 1 1 0 0 0 0 0 0 6 p s o 0 0 0 0 0 0 0 0 1 0 0 1 p s y 0 0 0 0 1 1 1 0 1 0 0 1 1 0 0 0 c p w 1 0 1 1 0 0 0 1 0 1 0 0 0 e p w t 0 0 0 0 0 0 0 0 0 p w x 0 0 0 0 1 1 0 0 1 0 1 0 0 0 1 1 0 0 0 8 p w y 0 0 0 0 1 1 1 0 1 0 0 1 1 0 0 0 c p w 1 6 0 0 0 0 1 0 0 0 0 0 1 p w 1 7 0 0 0 0 1 0 0 0 0 0 1 r 0 0 0 0 0 0 0 0 1 0 0 0 1 2 r u 0 0 0 0 0 0 1 0 0 0 0 1 0 2 r y 0 0 0 0 1 1 1 0 1 1 0 0 e r u o 0 0 0 0 0 0 0 1 0 0 0 0 1 r u x 0 0 1 0 0 0 0 0 0 0 0 1 r y 9 1 0 0 0 0 0 0 0 0 2 r y a 0 0 1 0 0 0 0 0 0 0 0 1 r y e 1 1 0 0 0 0 0 0 0 0 4 r y k 1 1 0 0 0 0 0 0 0 0 2 r y o 0 0 0 0 0 0 0 1 0 0 0 0 1 r y s 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 2 r y t 0 0 1 0 0 0 0 0 0 0 0 1 r y v 0 1 0 0 0 0 0 0 0 0 1 q 0 0 0 0 0 0 1 1 0 0 0 1 0 0 3 r y w 1 0 0 0 0 0 0 1 1 0 0 0 0 3 r u x 3 0 0 0 0 1 0 0 0 0 0 0 0 1 q o 0 0 0 0 0 0 0 1 0 0 1 1 4 r y 9 1 0 0 1 1 1 0 0 0 0 0 9 q p 0 0 0 0 0 0 0 1 0 0 0 1 r y 9 3 0 0 0 0 1 0 0 0 0 0 0 0 1 q w 1 0 0 0 0 0 0 0 1 0 0 0 1 1 4 r y s 3 0 0 0 0 1 0 0 0 0 0 0 0 1 q o s 0 0 1 0 0 0 0 0 0 0 0 1 2 r y t 3 0 0 0 0 1 0 0 0 0 0 0 0 1 q o u 0 0 0 0 0 0 0 1 0 0 0 1 1 3 r y v 2 0 0 0 0 1 0 0 0 0 0 0 3 q o x 0 0 1 0 0 0 0 0 1 1 0 0 1 0 1 0 0 0 1 1 0 0 0 9 r y w 1 0 0 1 1 1 0 0 0 0 0 9 q o y 0 0 0 0 1 1 1 0 1 0 0 0 1 1 1 0 0 0 e r y 9 1 6 0 0 0 0 1 0 0 0 0 0 1 q p s 0 0 1 0 0 0 0 0 0 0 0 1 2 r y 9 1 7 0 0 0 0 1 0 0 0 0 0 1 q w 1 0 1 1 1 1 0 0 0 1 0 1 0 0 0 f r y w 1 6 0 0 0 0 1 0 0 0 0 0 1 q w t 0 0 1 0 0 0 0 0 0 0 0 1 2 r y w 1 7 0 0 0 0 1 0 0 0 0 0 1 q w x 0 0 1 0 0 0 0 0 1 1 0 0 1 0 1 0 0 0 1 1 0 0 0 9 q w y 0 0 0 0 1 1 1 0 1 0 0 0 1 1 1 0 0 0 e q w 1 6 0 0 0 0 1 0 0 0 0 0 1 q w 1 7 0 0 0 0 1 0 0 0 0 0 1

G 7: All Shortest Paths (SPs) s-y s 10 20 31 40 50 60 G 7: All Shortest Paths (SPs) s-y s 10 20 31 40 50 60 70 80 90 A 0 B 0 C 0 D 0 E 0 F 0 G 0 H 0 I 0 J 0 K 0 L 0 M 0 N 0 O 1 P 1 Q 0 R 0 S 0 T 0 U 0 V 0 W 0 X 0 y 1 4 w 1 0 0 0 0 0 0 1 1 0 0 0 1 1 6 s 3 1 1 0 0 0 1 1 1 0 0 0 0 0 1 0 0 0 1 0 9 w 1 0 1 1 1 1 0 0 0 1 0 1 0 0 0 f s o 0 0 0 0 0 0 0 1 0 3 w p 0 0 0 0 0 0 0 1 0 0 0 1 s p 0 0 0 0 0 0 0 1 0 0 2 w q 0 0 0 0 0 0 1 0 0 0 0 0 1 s y 0 0 0 0 1 1 1 0 1 0 0 0 1 1 1 1 0 0 e w t 0 0 1 0 0 0 0 0 0 0 0 1 s 3 1 0 0 1 1 1 0 0 0 0 0 0 0 8 w x 0 0 1 0 0 0 0 0 1 1 0 0 1 0 1 1 0 0 0 a s 3 2 0 0 0 0 0 1 0 0 0 0 2 w y 0 0 0 0 1 1 1 0 1 1 0 0 0 e s 3 4 0 0 0 1 0 0 0 0 0 0 1 w 1 6 0 0 0 0 1 0 0 0 0 0 1 s 3 1 6 0 0 0 0 1 0 0 0 0 0 1 w 1 7 0 0 0 0 1 0 0 0 0 0 1 s 3 1 7 0 0 0 0 1 0 0 0 0 0 1 t 0 0 1 0 0 0 0 0 0 0 1 0 1 3 x 0 0 1 0 0 0 0 0 1 1 0 0 1 0 1 1 0 0 0 1 1 1 0 0 b x 3 1 1 0 1 0 0 0 0 0 0 0 1 1 0 0 0 8 t 3 1 1 0 0 0 1 1 1 0 0 0 0 1 0 0 1 0 9 x 9 1 0 0 0 0 0 0 0 0 1 2 t w 1 0 0 0 0 0 0 1 1 0 0 0 1 0 4 x f 0 0 0 0 0 0 0 0 0 1 1 t y 0 0 0 0 1 1 1 0 1 1 0 0 0 e x g 0 0 0 0 0 0 0 0 0 1 1 t 3 1 0 0 1 1 1 0 0 0 0 0 0 0 8 x j 0 0 0 0 0 0 0 0 0 1 1 t 3 2 0 0 0 0 0 1 0 0 0 0 2 x l 0 0 0 0 0 0 0 0 0 1 1 t 3 4 0 0 0 1 0 0 0 0 0 0 1 x n 0 0 0 0 0 0 0 0 0 1 1 t w 1 0 0 1 1 1 0 0 0 0 0 0 0 8 x o 0 0 0 0 0 0 0 1 0 0 0 1 3 t 3 1 6 0 0 1 1 1 0 0 0 0 0 0 0 8 x u 0 0 0 0 0 0 0 1 0 0 0 1 2 t 3 1 7 0 0 1 1 1 0 0 0 0 0 0 0 8 x v 0 1 0 0 0 0 0 0 0 0 1 2 t w 1 6 0 0 0 0 1 0 0 0 0 0 3 x w 1 0 0 0 0 0 0 1 1 0 0 0 0 1 5 u 0 0 0 0 0 0 1 0 0 0 1 1 4 t w 1 7 0 0 0 1 1 0 0 0 0 0 0 0 3 x 3 1 0 0 1 1 1 0 0 0 0 1 0 1 0 0 0 9 x 3 2 0 0 0 0 0 1 0 1 0 0 0 3 x 3 4 0 0 0 1 0 0 0 0 0 0 1 u o 0 0 0 0 0 0 0 1 0 1 0 0 3 u r 0 0 0 0 0 0 0 0 1 0 0 1 u x 0 0 1 0 0 0 0 0 1 1 0 0 1 0 1 0 0 9 u y 0 0 0 0 1 1 1 0 1 0 0 1 1 1 0 0 d u o q 0 0 0 0 0 0 1 0 0 0 0 0 1 u o s 0 0 0 0 0 0 1 0 0 0 0 0 1 u x 3 1 1 0 0 0 0 0 0 0 0 4 u x 9 1 0 0 0 0 0 0 0 0 0 1 u x w 1 0 0 0 0 0 0 1 0 0 0 0 0 2 u y 9 1 0 0 0 0 0 0 0 0 0 1 u y e 1 1 0 0 0 0 0 0 0 0 3 u y k 1 1 0 0 0 0 0 0 0 0 2 u y s 0 0 0 0 0 0 1 0 0 0 0 0 1 u y w 1 0 0 0 0 0 0 1 0 0 0 0 0 2 u x 3 1 0 0 1 1 1 0 0 0 0 0 0 0 8 u x 3 2 0 0 0 0 0 1 0 0 0 0 2 u x 3 4 0 0 0 1 0 0 0 0 0 0 1 u x 9 1 0 0 1 1 1 0 0 0 0 0 0 0 8 x 9 1 0 0 1 1 1 0 0 0 0 1 0 1 0 0 0 9 x 9 y 0 0 0 0 0 1 0 0 0 0 1 x f y 0 0 0 0 0 1 0 0 0 0 1 x g y 0 0 0 0 0 1 0 0 0 0 1 x j y 0 0 0 0 0 1 0 0 0 0 1 x l y 0 0 0 0 0 1 0 0 0 0 1 x n y 0 0 0 0 0 1 0 0 0 0 1 x o y 0 0 0 0 0 1 0 0 0 0 1 x u y 0 0 0 0 0 1 0 0 0 0 1 x v 2 0 0 0 0 0 1 0 1 0 0 0 3 x v y 0 0 0 0 0 1 0 0 0 0 1 x w 1 0 0 1 1 1 0 0 0 0 1 0 1 0 0 0 9 x w y 0 0 0 0 0 1 0 0 0 0 1 x 3 1 6 0 0 0 0 1 0 0 0 0 0 1 x 3 1 7 0 0 0 0 1 0 0 0 0 0 1 x 9 1 6 0 0 0 0 1 0 0 0 0 0 1 x 9 1 7 0 0 0 0 1 0 0 0 0 0 1 x w 1 6 0 0 0 0 1 0 0 0 0 0 1 x w 1 7 0 0 0 0 1 0 0 0 0 0 1 u x w 1 0 0 1 1 1 0 0 0 0 0 0 0 8 u y 9 1 0 0 0 0 1 1 1 0 0 0 0 1 0 0 0 0 0 0 8 u y e 2 0 0 0 0 0 1 0 0 0 0 2 u y e 4 0 0 0 1 0 0 0 0 0 0 1 u y k 1 0 0 1 1 1 0 0 0 0 0 0 0 8 u y k 2 0 0 0 0 0 1 0 0 0 0 2 u y w 1 0 0 1 1 1 0 0 0 0 0 0 0 8 u x 3 1 6 0 0 0 0 1 0 0 0 0 0 1 u x 3 1 7 0 0 0 0 1 0 0 0 0 0 1 u x 9 1 6 0 0 0 0 1 0 0 0 0 0 1 u x 9 1 7 0 0 0 0 1 0 0 0 0 0 1 u x w 1 6 0 0 0 0 1 0 0 0 0 0 1 u x w 1 7 0 0 0 0 1 0 0 0 0 0 1 u y 9 1 6 0 0 0 0 1 0 0 0 0 0 1 u y 9 1 7 0 0 0 0 1 0 0 0 0 0 1 u y e 1 6 0 0 0 0 1 0 0 0 0 0 1 u y e 1 7 0 0 0 0 1 0 0 0 0 0 1 u y k 1 6 0 0 0 0 1 0 0 0 0 0 1 u y k 1 7 0 0 0 0 1 0 0 0 0 0 1 u y w 1 6 0 0 0 0 1 0 0 0 0 0 1 u y w 1 7 0 0 0 0 1 0 0 0 0 0 1 1 2 3 4 5 6 7 8 9 a b c d e f g h i j k l m n o p q r s t u v w x y y 0 0 0 0 1 1 1 0 1 1 0 0 1 1 1 0 0 g y 9 1 0 0 0 0 0 0 0 0 1 0 3 y a 0 0 1 0 0 0 0 0 0 0 0 1 y e 1 1 0 0 0 0 0 0 0 0 4 y f 0 0 0 0 0 0 0 0 1 0 1 y g 0 0 0 0 0 0 0 0 1 0 1 y j 0 0 0 0 0 0 0 0 1 0 1 y k 1 1 0 0 0 0 0 0 0 0 2 y l 0 0 0 0 0 0 0 0 1 0 1 y n 0 0 0 0 0 0 0 0 1 0 1 y o 0 0 0 0 0 0 0 1 0 0 0 1 0 2 y s 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 2 y t 0 0 1 0 0 0 0 0 0 0 0 1 y u 0 0 0 0 0 0 0 0 1 0 1 y v 0 1 0 0 0 0 0 0 0 0 1 0 2 y w 1 0 0 0 0 0 0 1 1 0 0 0 1 0 4 y 9 1 0 0 1 1 1 0 0 0 0 0 9 y 9 3 0 0 0 0 1 0 0 0 0 0 0 0 1 y a 3 0 0 0 0 1 0 0 0 0 0 0 0 1 1 2 3 4 5 6 7 8 9 a b c d e f g h i j k l m n o p q r s t u v w x y y k 1 0 0 1 1 1 0 0 0 0 0 9 y k 2 0 0 0 0 1 0 0 0 0 0 0 3 v 0 1 0 0 0 0 0 0 0 1 1 4 y s 3 0 0 0 0 1 0 0 0 0 0 0 0 1 v 2 1 0 1 1 0 0 0 0 0 1 0 1 0 0 0 0 8 y t 3 0 0 0 0 1 0 0 0 0 0 0 0 1 v 9 1 0 0 0 0 0 0 0 0 2 y v 2 0 0 0 0 1 0 0 0 0 0 0 3 v x 0 0 1 0 0 0 1 1 0 0 1 0 1 1 0 0 0 1 0 0 9 y w 1 0 0 1 1 1 0 0 0 0 0 9 v y 0 0 0 0 0 1 1 1 0 0 1 1 0 1 0 0 e y 9 1 6 0 0 0 0 1 0 0 0 0 0 1 v 2 1 0 0 1 1 1 0 0 0 0 0 0 6 y 9 1 7 0 0 0 0 1 0 0 0 0 0 1 v 2 4 0 0 0 1 0 0 0 0 0 0 1 y k 1 6 0 0 0 0 1 0 0 0 0 0 1 v 9 1 0 0 1 1 1 0 0 0 0 0 0 6 y k 1 7 0 0 0 0 1 0 0 0 0 0 1 v x o 0 0 0 0 0 0 0 1 0 0 0 0 1 y w 1 6 0 0 0 0 1 0 0 0 0 0 1 v x w 0 0 0 0 0 0 1 1 0 0 0 0 2 y w 1 7 0 0 0 0 1 0 0 0 0 0 1 v y o 0 0 0 0 0 0 0 1 0 0 0 0 1 v y s 0 0 0 0 0 0 1 0 0 0 0 0 1 v y w 0 0 0 0 0 0 1 1 0 0 0 0 2 v 2 1 6 0 0 0 0 1 0 0 0 0 0 1 v 2 1 7 0 0 0 0 1 0 0 0 0 0 1 v 9 1 6 0 0 0 0 1 0 0 0 0 0 1 v 9 1 7 0 0 0 0 1 0 0 0 0 0 1

G 7: Friendships in Zachery’s Karate Club. 1 1 1 3 3 9 1 G 7: Friendships in Zachery’s Karate Club. 1 1 1 3 3 9 1 2 3 6 7 9 e k w s x x g 1 4 1 1 3 1 1 5 1 7 7 1 9 y 8 1 e y 8 1 k y 8 1 w q 1 1 w x 7 1 2 w 2 2 2 1 y 2 1 3 4 e k v 6 8 9 8 5 1 1 1 3 3 3 3 3 2 3 3 3 3 3 1 1 1 9 a s s s v y 3 1 2 4 8 9 a e s t 6 7 w y y o p y 8 a b 4 1 0 2 1 1 3 2 1 1 1 7 7 2 1 7 6 6 6 6 6 5 5 5 5 5 7 7 6 6 6 1 1 1 1 1 5 5 5 1 1 1 1 1 7 7 7 1 1 6 6 6 1 1 1 3 3 9 9 e k w w w 5 5 5 1 1 1 3 3 9 9 e k w w w 7 1 5 6 2 3 6 1 7 b 2 3 9 e k w s x x y y y q x y 5 1 7 b 2 3 9 e k w s x x y y y q x y 4 d 1 1 1 4 3 1 1 5 1 7 7 8 8 8 1 7 8 3 d 2 1 1 4 3 1 1 5 1 7 7 8 8 8 1 7 8 8 8 8 8 8 8 8 1 1 2 2 2 3 3 3 4 9 9 9 9 9 8 8 1 1 1 2 2 2 3 3 3 4 9 e k w e k v 9 a e s t e 9 9 9 1 1 1 3 x x y y y 8 1 2 3 4 6 7 9 e k w e k v 9 a e s t x e y y y y 9 1 3 v x y 6 7 w s o w o s w 4 c 5 6 2 1 1 1 1 1 3 1 7 1 1 1 1 5 e 7 1 8 e 1 1 2 2 1 1 2 c c c c c b b b b b c c c c 1 1 1 1 1 d d d d d b b b 1 1 1 1 1 c 1 1 1 1 3 3 9 9 e k w w w d d 1 1 1 1 4 4 b b b 1 1 1 3 3 9 9 e k w w w c 1 2 3 6 7 9 e k w s x x y y y q x y d 1 4 2 3 6 7 9 e k w 2 3 b 1 5 6 2 3 9 e k w s x x y y y q x y 2 e 4 1 1 3 1 1 5 1 4 3 d 1 2 0 4 3 1 1 5 1 7 7 8 8 8 1 7 8 1 g 1 4 1 1 3 1 1 5 1 7 7 8 8 8 1 7 8 f f f e e e e f f x x x y y y y g e e e 1 1 1 3 y y y e 1 2 3 4 y 6 7 w s o s w f x y 3 9 o v w 9 e k o s v w g x 5 c 5 6 2 f 1 1 2 1 1 1 2 2 a f 4 1 1 1 3 2 a h h h h h i i h h h 6 6 6 6 6 7 7 7 7 7 i i i 1 1 h h 6 6 6 7 7 7 1 1 1 1 1 i i 1 1 1 1 2 2 3 3 h h 6 7 1 1 1 3 3 9 9 e k w w w h 6 7 1 1 2 3 9 e k w s x x y y y q x y i 1 2 3 6 7 9 e k w 3 e k v s x 2 2 2 c c 1 4 3 1 1 5 1 7 7 8 8 8 1 7 8 2 e 7 4 1 1 2 1 1 5 4 1 1 2 1 7 j j j f x x j x y 3 9 2 a f 4 1 o o o o q s u x y w 3 5 3 3 2 a e 1 4 q q o q o p w s 3 4 1 4 2 o x 3 4 q o u 3 o x 9 1 q o x 9 o x v 1 q o y e o x w 1 q p s 2 o y 9 1 q w 1 f o y e 3 q w t 2 u u u o r x y q 4 3 1 9 d 1 o y k 2 q w x 9 u o s 1 o y v 1 q w y e u x 3 4 o y w 1 q w 1 6 1 u x 9 1 o q w 1 8 q w 1 7 1 u x w 2 j x o 1 o s 3 1 8 j x v 1 o s 3 2 2 r r u 2 2 u y 9 1 u y e 3 2 1 7 1 2 1 w 2 2 3 s 2 2 3 x 7 2 e y 8 2 k y 8 j y 9 1 j y e 3 j y k 2 j y o 1 j y s 1 j y v 1 j y w 3 k 1 6 1 3 t w 1 3 t 4 4 y 4 1 2 3 e 7 6 a 4 5 1 7 7 7 1 1 1 3 3 9 e k w s x x 1 1 5 1 7 7 g y f a 2 d 1 3 s 1 g x 3 4 a 3 9 d 1 3 x 7 g x 9 1 a y f d 1 9 x 7 g x o 1 a 3 1 8 d 1 9 y 8 g x v 1 a 3 2 2 d 1 e y 8 g x w 3 a 3 4 1 d 1 k y 8 g y 9 1 a 3 s 1 d 1 w q 1 g y e 3 a y o 1 d 1 w x 7 g y k 2 a y s 1 d 1 w y 8 g y o 1 a y w 2 d 4 3 s 1 g y s 1 4 3 x 7 7 1 w x 7 a 3 1 6 1 d 4 3 x 7 g y v 1 i 1 9 x 7 i 1 9 y 8 i 1 e y 8 i 1 k y 8 i 1 w q 1 i 1 w x 7 i 1 w y 8 i 2 3 s 1 i 2 3 x 7 i 2 e y 8 i 2 k y 8 i 2 v x 7 7 1 9 3 d 4 e 1 4 1 6 1 7 1 9 y 8 4 1 7 1 e y 8 4 1 w 2 7 1 k y 8 4 3 s 2 7 1 w q 1 4 e y 8 7 1 w y 8 a 3 1 7 1 d 4 e y 8 g y w 3 i 2 v y 8 k k k k l l l 1 1 1 2 2 y y y l f x x x y y y y 7 9 w 3 v 9 f g j l n o s u v w l x y 3 9 o v w 9 e k o s v w 1 1 3 1 1 1 1 2 1 1 1 3 2 a f 4 1 1 1 3 2 1 1 1 3 m m m m m m m 1 1 1 1 1 2 2 2 n n n m m 1 1 1 1 2 2 3 3 9 9 e k w w w 3 3 e k v v n n x x x y y y y m 1 2 3 6 7 9 e k w 3 e k v s x x y y y q x y s x y y x y n x y 3 9 o v w 9 e k o s v w 2 e 7 4 1 1 2 1 1 5 4 1 1 2 1 7 7 8 8 8 1 7 8 8 7 8 2 a f 4 1 1 1 3 2 1 1 1 3 o o o o o p p o o o o q q s s x x x y y y y p p p p w w s x x x y y y y w w 3 3 9 9 w w 9 9 e e k k w w 3 3 9 v w 9 e e e k k v w 1 1 1 1 1 p p p q s s s w w 1 1 4 1 2 1 1 1 2 4 1 2 2 1 6 7 6 7 6 7 p q s w o 3 o y 1 t x y 6 7 1 8 2 8 8 8 2 1 8 2 2 8 1 1 1 1 13 1 3 4 1 6 1 c e 0 8 c 1 1 r r s s t t r r r r y y s s s 3 3 t t 3 3 w w r r r u y y y 9 9 w w s s 3 3 3 1 1 t t t 3 3 3 w 1 1 r u u y y y y y x 9 9 s t v w 1 1 y o x 9 a e k o s t v w 3 1 3 3 3 2 1 6 7 s 3 o p y 1 2 4 6 7 t 3 w y 1 2 4 1 6 7 e 1 1 2 1 4 2 1 1 3 1 9 1 1 1 3 9 1 1 4 9 3 2 e 8 2 1 1 1 3 9 4 e 8 2 1 8 8 8 3 3 u u u u v v u u u x x x y y y y v v v v 2 2 9 9 u u u x x x y y y y 3 3 9 9 w w 9 9 e e k k w w v v 2 2 9 x x y y y 1 1 y y y 3 3 3 9 w 9 e e e k k w 1 1 1 1 k s w 1 2 4 1 2 1 6 7 6 7 v 2 9 x y 1 4 1 o w o s w 6 7 2 1 2 8 2 1 8 2 8 1 1 1 1 4 8 2 9 e 6 1 2 1 1 1 1 x x x w w x x x x 3 3 9 9 w w w w 1 1 x x x 3 3 3 9 9 f g j l n o u v v w w 1 1 1 w 1 p q t x y 6 7 x 3 9 f g j l n o u v w 1 2 4 1 y y y y 2 y 1 y 6 7 6 7 6 f 1 1 1 a e 1 1 b 8 2 1 1 1 3 2 2 5 9 3 1 9 1 1 1 1 y y y y 9 9 k k w w y y y y 9 9 a k k s t v w 1 1 1 y 9 a e f g j k l n o s t u v w 1 3 3 1 2 3 3 2 1 6 7 6 7 g 3 1 4 1 1 1 2 2 1 1 2 4 9 1 1 9 3 1 1 3 9 1 1 1 j x w 3 k k 1 k 1 2 y 3 3 e 7 f 1 2 v x 7 All SPCs.

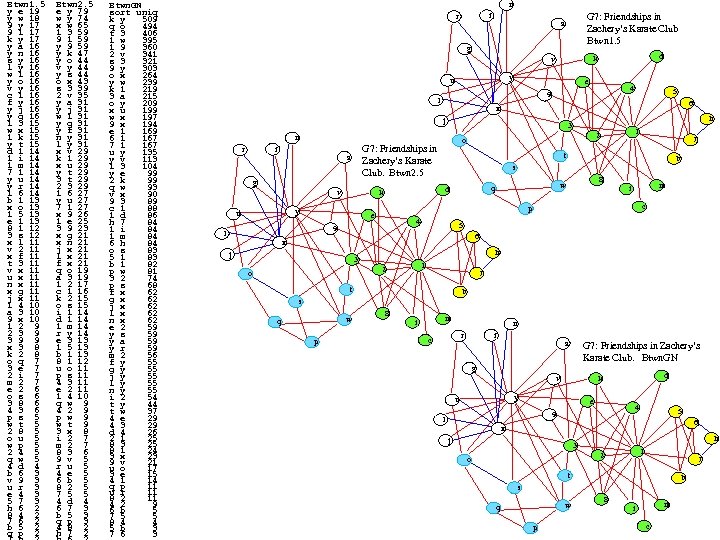Btwn 1. 5 y e 19 y w 18 9 y 17 9 1 Btwn 1. 5 y e 19 y w 18 9 y 17 9 1 17 k y 17 y a 16 y n 16 s y 16 l y 16 w 1 16 y o 16 v y 16 c 1 16 f y 16 y j 16 y g 16 1 3 15 w x 15 1 k 15 y t 15 d 1 14 1 i 14 1 m 14 7 1 14 y u 14 y r 14 1 6 14 b 1 13 x o 13 1 5 13 e 1 13 8 1 12 3 s 12 x l 11 v 2 11 x f 11 t 3 11 v x 11 u x 11 n x 11 x g 11 j x 11 1 4 10 a 3 10 9 x 10 1 2 9 2 3 9 9 x 3 8 k 2 8 o q 7 3 e 7 2 i 7 m 2 7 e 2 6 o s 6 3 8 6 4 3 6 p s 5 w t 5 2 8 5 o u 5 w p 5 2 4 5 q w 5 4 d 4 b 6 3 v 9 3 u r 3 e 4 3 5 7 3 h 6 2 8 4 2 7 6 2 b 5 2 q p 2 Btwn 2. 5 e y 79 w y 74 x w 65 1 3 59 9 1 59 y 9 59 y k 47 y o 44 v y 44 y s 44 o x 43 s 3 39 2 v 35 y a 31 y j 31 w 1 31 y g 31 y f 31 n y 31 l y 31 x v 29 k 1 29 x u 29 y t 29 3 t 29 2 3 29 1 6 27 y u 27 7 1 27 x 9 26 1 e 25 3 9 23 x g 21 x n 21 j x 21 l x 21 f x 21 q o 19 a 3 19 1 2 17 c 1 16 k 2 15 o s 15 i 1 14 d 1 14 1 m 14 r y 14 e 3 13 1 5 13 b 1 13 8 1 12 u o 11 p s 11 4 3 11 e 2 11 1 4 10 q w 9 4 2 9 p w 9 w t 9 3 x 8 i 2 7 m 2 7 8 3 6 9 v 5 r u 5 4 e 5 6 b 5 8 2 5 7 5 5 4 d 4 6 7 3 b 5 3 q p 3 4 8 2 h 7 2 Btwn. GN sort uniq k y 509 q o 494 t 3 406 1 w 395 1 9 360 2 v 341 s 3 321 9 y 303 o x 264 y w 239 k 1 219 3 a 215 o y 209 x u 199 w x 197 9 x 194 e 1 169 6 1 167 7 1 167 u y 135 y v 113 1 3 104 y e 99 2 k 99 q w 93 v x 90 9 3 89 c 1 88 1 d 86 h 7 84 1 i 84 1 m 84 6 h 84 o s 83 5 1 83 b 1 82 p w 81 3 2 74 p s 68 f x 62 g x 62 j x 62 l x 62 n x 62 e 2 59 y s 59 y a 59 y r 59 m 2 56 f y 55 g y 55 j y 55 l y 55 n y 55 i 2 54 t y 44 t w 37 4 e 29 4 3 29 d 4 26 2 1 25 8 3 25 8 1 24 3 x 23 9 v 21 u o 17 3 e 15 4 1 14 q p 11 u r 11 8 2 11 4 2 9 6 b 5 7 5 5 8 4 4 5 b 3 7 6 3 n f r G 7: Friendships in Zachery’s Karate Club Btwn 1. 5 a g y u e 6 y u b 8 w q m i c p 4 9 l t d e 7 s k v 1 2 o G 7: Friendships in Zachery’s Karate Club. Btwn 2. 5 g h 3 n a 5 x j r 4 9 l f d k v 5 6 x j h 3 1 2 o 7 t b s w q p 8 m i n f r c a G 7: Friendships in Zachery’s Karate Club. Btwn. GN g y u d k v e 4 9 l 5 6 x j h 3 1 2 o 7 t b s w q p 8 m i c

Recomputing Between-nesses after every delete? GN does this. Can it be done by just Recomputing Between-nesses after every delete? GN does this. Can it be done by just updating the existing btwn-nesses is some way? 1 2 3 4 Edges Map V 1 V 2 E 1, 1 0 1, 2 0 1, 3 1 1, 4_ 1_ 2, 1 0 2, 2 0 2, 3 0 2, 4_ 1_ 3, 1 1 3, 2 0 3, 3 0 3, 4_ 1_ 4, 1 1 4, 2 1 4, 3 1 4, 4 0 2 -Level Stride=4, Edge p. Tree Level 1 1 1 E 1 0 0 1 1 E 2 E 3 0 1 0 0 1 1 E 4 1 1 1 0 0 1 1 2 0 0 0 1 3 1 0 0 1 4 1 1 1 0 2 1 2 3 4 4 4 0 1 0 1 Btwn 14=1 0 1 0 Btwn 24=2 0 0 0 Btwn 34=1 1 2 1 If 24 is deleted, it appears to be easy, namely, turn off bit 4 in 2 and bit 2 in 4, delete all three 2 hop SPs since they all three involve 24. So at this point it looks like it might just be a matter of deleting those SPs that involve the edge (either at the beginning, end or middle). However, if we delete 14 then 134 and 1342 are barnd new SPs which weren’t there before. It looks like one has to start fresh computing Between-ness? ? ? Ek is the map of edge endpoints from k (points adjacent to k). Shi is the map of endpoints of 2 -hop Shortest Paths Through h then i. Of course, |Shi&Ek|=0 since there is a SP of length<2 to each vertex in Ek. Shij is the map of endpoints of 3 -hop Shortest Paths Through h then i then j. Of course, |Shij&Ek|=|Shij&Shi|=0 since there is a SP of length<3 to each Ek and Shi. Etc. The Main Theorem: The full SP participation count of hk is a + b + ab where a is |Shk|+|Shkij|+… and b is |Skh|+|Skhij|+…. Proof: Let s=c…dhke…f by any SP in which hk participates. If h=c then s is counted in |Shk|+|Shkij|+… If k=f then hk is counted in c then hk is counted in |Skh|+|Sikh|+|Sjikh|+…. If h c and k f then hk occurs in the middle of s and the “left half” of s (hk and left) is counted in a = |Skh|+|Sikh|+|Sjikh|+… and the “right half” (hk and right) is counted in b = |Shk|+|Shkij|+… therefore s is counted in ab. Thus Participation Count of hk a + b + ab. But every a + b + ab counts a SP, so we get =.

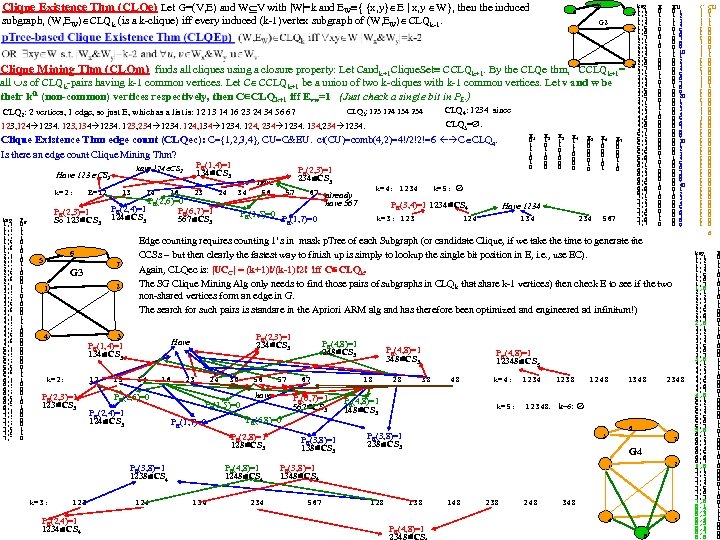Clique Existence Thm (CLQe) Let G=(V, E) and W V with |W|=k and EW Clique Existence Thm (CLQe) Let G=(V, E) and W V with |W|=k and EW { {x, y} E | x, y W}, then the induced subgraph, (W, EW) CLQk (is a k-clique) iff every induced (k-1)vertex subgraph of (W, EW) CLQk-1. key 1, 1 1, 3 1, 4 2 1, 5 1, 6 1, 7 2, 1 2, 2 2, 3 2, 4 2, 5 3 2, 6 2, 7 3, 1 3, 2 3, 3 3, 4 3, 5 3, 6 3, 7 4, 1 4, 2 4, 3 4, 4 4, 5 4, 6 4, 7 5, 1 5, 2 5, 3 5, 4 5, 5 5, 6 5, 7 6, 1 6, 2 6, 3 6, 4 6, 5 6, 6 6, 7 7, 1 7, 2 7, 3 7, 4 7, 5 7, 6 7, 7 6 5 7 1, 2 G 2 1 4 Clique Mining Thm (CLQm) finds all cliques using a closure property: Let Candk+1 Clique. Set CCLQk+1. By the CLQe thm, CCLQk+1= all s of CLQk-pairs having k-1 common vertices. Let C CCLQk+1 be a union of two k-cliques with k-1 common vertices. Let v and w be their kth (non-common) vertices respectively, then C CLQk+1 iff Evw=1 (Just check a single bit in PE. ) CLQ 2: 2 vertices, 1 edge, so just E, which as a list is: 12 13 14 16 23 24 34 56 67 CLQ 3: 123 124 134 234 CLQ 4: 1234 since CLQ 5=. 123, 124 1234. 123, 134 1234. 123, 234 1234. 124, 134 1234. 124, 234 1234. 134, 234 1234. Clique Existence Thm edge count (CLQec): C={1, 2, 3, 4}, CU=C&EU. ct(CU)=comb(4, 2)=4!/2!2!=6 C CLQ 4. Is there an edge count Clique Mining Thm? k=2: key 1, 1 1, 2 1, 3 1, 4 1, 5 1, 6 1, 7 2, 1 2, 2 2, 3 2, 4 2, 5 2, 6 2, 7 3, 1 3, 2 3, 3 3, 4 3, 5 3, 6 3, 7 4, 1 4, 2 4, 3 4, 4 4, 5 4, 6 4, 7 5, 1 5, 2 5, 3 5, 4 5, 5 5, 6 5, 7 6, 1 6, 2 6, 3 6, 4 6, 5 6, 6 6, 7 7, 1 7, 2 7, 3 7, 4 7, 5 7, 6 7, 7 PE 0 1 1 1 0 1 0 1 1 0 0 0 1 1 1 0 0 0 0 0 1 1 1 0 0 0 1 1 0 E=12 PE(2, 3)=1 So 123 CS 3 13 7 G 3 2 1 4 14 PE(2, 4)=1 124 CS 3 6 5 16 PE(2, 3)=1 123 CS 3 13 24 34 PE(2, 4)=1 1234 CS 4 PE(3, 4)=1 1234 CS 4 k=3: 123 PE(1, 7)=0 E 3 1 1 0 0 0 E 4 1 1 1 0 0 E 5 0 0 0 1 0 E 6 1 0 0 0 1 E 7 0 0 1 1 0 k=5: k=4: 1234 67. already have 567 PE(2, 3)=1 234 CS 3 Have 14 16 PE(2, 6)=0 PE(2, 4)=1 124 CS 3 24 34 23 56 have PE(1, 7)=0 124 57 67 PE(6, 8)=0 PE(4, 8)=1 1248 CS 4 134 PE(4, 8)=1 248 CS 3 PE(6, 7)=1 567 CS 3 PE(1, 5)=0 PE(3, 8)=1 1238 CS 4 123 57 PE(1, 5)=0 PE(2, 8)=1 128 CS 3 k=3: PE(2, 3)=1 234 CS 3 Have 56 E 2 1 0 1 1 0 0 0 Have 1234 124 134 234 567 EU 0 1 1 2 1 3 1 4 0 5 1 6 0 7 0 8 0 9 1 10 1 1 0 2 0 3 0 4 0 5 0 6 0 7 1 8 0 9 0 20 0 1 0 2 0 3 0 4 0 5 0 6 0 7 0 8 0 9 0 30 0 1 0 2 0 3 1 4 0 5 0 6 0 7 0 8 0 9 0 40 0 1 1 2 0 3 0 4 0 5 0 6 0 7 0 8 0 9 Edge counting requires counting 1’s in mask p. Tree of each Subgraph (or candidate Clique, if we take the time to generate the CCSs – but then clearly the fastest way to finish up is simply to lookup the single bit position in E, i. e. , use EC). Again, CLQec is: |UCC| = (k+1)!/(k-1)!2! iff C CLQk. The SG Clique Mining Alg only needs to find those pairs of subgraphs in CLQ k that share k-1 vertices) then check E to see if the two non-shared vertices form an edge in G. The search for such pairs is standare in the Apriori ARM alg and has therefore been optimized and engineered ad infinitum!) 3 12 23 PE(2, 6)=0 PE(6, 7)=1 567 CS 3 PE(1, 4)=1 134 CS 3 k=2: PE(1, 4)=1 134 CS 3 have 124 CS 3 Have 123 CS 3 E 1 0 1 1 1 0 E 0 1 1 1 0 1 0 1 1 0 0 0 1 1 1 0 0 0 0 0 1 0 1 0 0 0 0 1 1 0 234 PE(4, 8)=1 348 CS 3 18 28 PE(4, 8)=1 12348 CS 5 38 48. PE(4, 8)=1 148 CS 3 k=4: k=5: 1234 1238 1248 1348 2348 12348. k=6: 6 PE(3, 8)=1 138 CS 3 PE(3, 8)=1 238 CS 3 5 1 128 138 PE(4, 8)=1 2348 CS 148 238 248 2 4 PE(3, 8)=1 1348 CS 4 567 7 G 4 3 348 8 C 1 1 1 1 0 0 0 0 0 0 0 0 0 key 1, 1 1, 2 1, 3 1, 4 1, 5 1, 6 1, 7 1, 8 2, 1 2, 2 2, 3 2, 4 2, 5 2, 6 2, 7 2, 8 3, 1 3, 2 3, 3 3, 4 3, 5 3, 6 3, 7 3, 8 4, 1 4, 2 4, 3 4, 4 4, 5 4, 6 4, 7 4, 8 5, 1 5, 2 5, 3 5, 4 5, 5 5, 6 5, 7 5, 8 6, 1 6, 2 6, 3 6, 4 6, 5 6, 6 6, 7 6, 8 7, 1 7, 2 7, 3 7, 4 7, 5 7, 6 7, 7 7, 8 8. 1 8, 2 8, 3 8, 4 8, 5 8, 6 8, 7 8. 8 CU 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 6 E 0 1 1 1 0 0 0 1 1 1 0 0 0 1 1 0 0 0 1 1 0 1 0 0 0 0 0 1 1 1 1 0 0

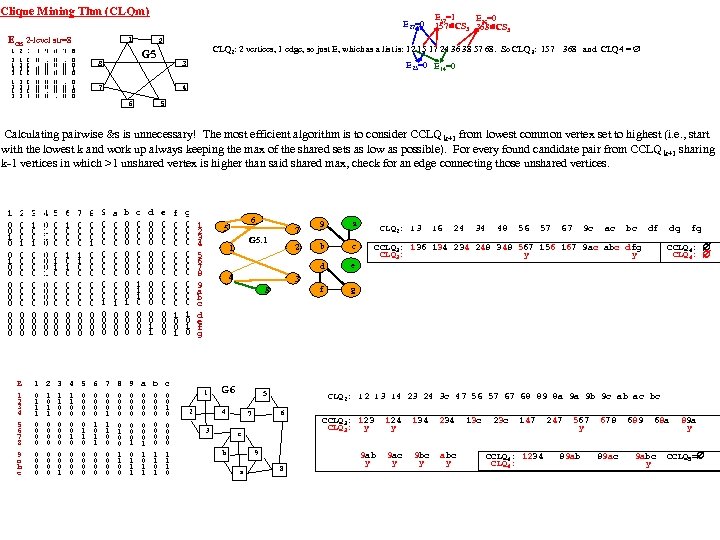Clique Mining Thm (CLQm) E 27=0 EG 5 2 -level str=8 1 0 0 Clique Mining Thm (CLQm) E 27=0 EG 5 2 -level str=8 1 0 0 1 0 2 1 0 0 0 0 3 0 0 0 1 4 0 1 0 0 0 5 1 0 0 0 1 0 6 0 0 1 7 1 0 0 0 1 8 0 0 1 0 0 2 CLQ 2: 2 vertices, 1 edge, so just E, which as a list is: 12 15 17 24 36 38 57 68. So CLQ 3: 157 368 and CLQ 4 = G 5 8 E 57=1 E 36=0 157 CS 3 368 CS 3 E 25=0 E 14=0 3 4 7 5 6 Calculating pairwise &s is unnecessary! The most efficient algorithm is to consider CCLQ k+1 from lowest common vertex set to highest (i. e. , start with the lowest k and work up always keeping the max of the shared sets as low as possible). For every found candidate pair from CCLQ k+1 sharing k-1 vertices in which >1 unshared vertex is higher than said shared max, check for an edge connecting those unshared vertices. 1 0 0 0 0 0 2 0 0 0 1 0 0 0 E 1 2 3 4 5 6 7 8 9 a b c 3 1 0 0 0 0 1 0 1 1 1 0 0 0 0 4 0 1 1 0 0 0 2 1 0 1 1 0 0 0 0 5 0 0 0 1 1 0 0 0 0 0 3 1 1 0 0 0 0 0 1 6 1 0 0 0 0 0 4 1 1 0 0 0 0 0 7 0 0 1 1 0 0 0 0 0 5 0 0 0 1 1 0 0 0 8 0 0 0 1 0 0 0 6 0 0 1 0 1 1 0 0 9 0 0 0 1 0 0 7 0 0 0 1 1 1 0 0 0 a 0 0 0 1 0 0 8 0 0 0 1 1 0 0 b 0 0 0 1 0 0 9 0 0 0 0 1 1 1 c 0 0 0 0 1 1 1 0 0 0 a 0 0 0 0 1 1 d 0 0 0 0 1 1 b 0 0 0 0 1 1 0 1 e 0 0 0 0 c 0 0 1 0 0 0 1 1 1 0 f 0 0 0 1 0 0 1 g 0 0 0 1 0 6 5 G 5. 1 1 2 4 G 6 5 4 2 3 b c e g CLQ 2: 13 16 24 34 48 56 57 67 9 c ac bc df dg fg CCLQ 4: CCLQ 3: 136 134 248 348 567 156 167 9 ac abc dfg CLQ 3: y y 3 8 1 a f 7 9 d 1 2 3 4 5 6 7 8 9 a b c d e f g CLQ 2: 12 13 14 23 24 3 c 47 56 57 67 68 89 8 a 9 a 9 b 9 c ab ac bc 6 7 c 9 b a 8 CCLQ 3: 123 CLQ 3: y 124 y 134 234 9 ab y 9 ac y 9 bc y abc y 13 c 23 c 147 CCLQ 4: 1234 CLQ 4: 247 567 y 89 ab 678 89 ac 689 68 a 9 abc y 89 a y CCLQ 5=

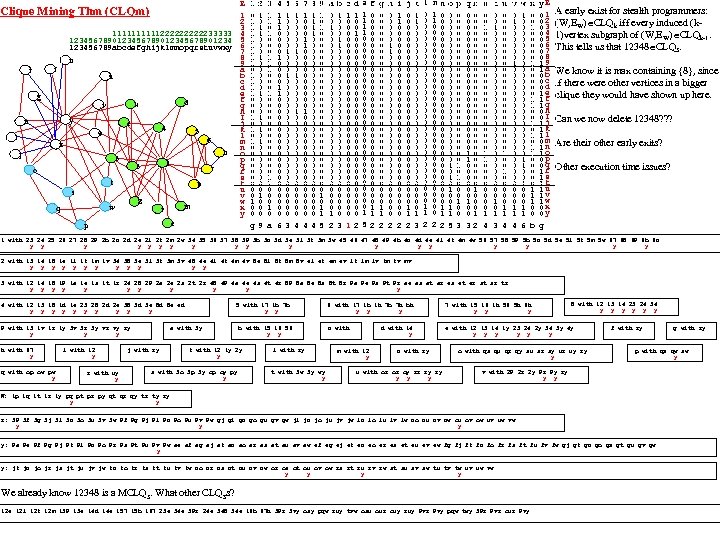E 1 2 3 111112222233333 4 123456789012345678901234 5 123456789 abcdefghijklmnopqrstuvwxy 6 7 8 n E 1 2 3 111112222233333 4 123456789012345678901234 5 123456789 abcdefghijklmnopqrstuvwxy 6 7 8 n 9 a f b a c d e f d k v g h I y e j 4 k 5 9 l 6 m x n h o 3 p 1 q 2 7 r s t t b u s v w 8 m w x q i y c p Clique Mining Thm (CLQm) r g u l j o 1 0 1 1 1 1 0 0 0 1 0 1 0 0 0 0 0 1 0 0 g 2 1 0 1 1 0 0 0 0 0 1 0 0 0 9 3 1 1 0 0 0 1 1 1 0 0 0 0 1 1 0 0 0 1 0 a 4 1 1 1 0 0 0 0 0 0 0 6 5 1 0 0 0 0 0 0 0 0 3 6 1 0 0 0 0 0 0 0 0 0 0 4 7 1 0 0 0 1 1 0 0 0 0 0 0 0 4 8 1 1 0 0 0 0 0 0 0 0 4 9 1 0 0 0 0 0 0 0 1 0 1 1 5 a 0 0 1 0 0 0 0 0 0 0 0 1 2 b 1 0 0 0 1 1 0 0 0 0 0 0 0 3 c 1 0 0 0 0 0 0 0 0 0 1 d 1 0 0 0 0 0 0 0 0 2 e 1 1 0 0 0 0 0 0 0 0 1 5 f 0 0 0 0 0 0 0 0 1 1 2 g 0 0 0 0 0 0 0 0 1 1 2 h 0 0 0 1 1 0 0 0 0 0 0 0 2 i 1 1 0 0 0 0 0 0 0 0 2 j 0 0 0 0 0 0 0 0 1 1 2 k 1 1 0 0 0 0 0 0 0 0 1 3 l 0 0 0 0 0 0 0 0 1 1 2 m 1 1 0 0 0 0 0 0 0 0 2 n 0 0 0 0 0 0 0 0 1 1 2 o 0 0 0 0 0 0 0 1 0 1 0 0 1 1 5 p 0 0 0 0 0 0 0 1 0 0 3 q 0 0 0 0 0 0 1 1 0 0 0 1 0 0 3 r 0 0 0 0 0 0 0 0 1 0 0 0 1 2 s 0 0 1 0 0 0 0 0 1 1 0 0 0 0 1 4 t 0 0 1 0 0 0 0 0 0 0 1 0 1 3 u 0 0 0 0 0 0 1 0 0 0 1 1 4 v 0 1 0 0 0 0 0 0 0 1 1 4 w 1 0 0 0 0 0 0 1 1 0 0 0 1 1 6 x 0 0 1 0 0 0 0 0 1 1 0 0 1 0 1 1 0 0 0 1 1 1 0 0 b y. E 01 02 03 04 05 06 07 08 19 1 a 0 b 0 c 0 d 1 e 1 f 1 g 0 h 0 I 1 j 1 k 1 l 0 m 1 n 1 o 0 p 0 q 1 r 1 s 1 t 1 u 1 v 1 w 0 x 0 y A early exist for stealth programmers: (W, EW) CLQk iff every induced (k 1)vertex subgraph of (W, E W) CLQk-1. This tells us that 12348 CLQ 5. We know it is max containing {8}, since if there were other vertices in a bigger clique they would have shown up here. Can we now delete 12348? ? ? Are their other early exits? Other execution time issues? g 1 with 23 24 25 26 27 28 29 2 b 2 c 2 d 2 e 2 i 2 k 2 m 2 w 34 35 36 37 38 39 3 b 3 c 3 d 3 e 3 i 3 k 3 m 3 w 45 46 47 48 49 4 b 4 c 4 d 4 e 4 i 4 k 4 m 4 w 56 57 58 59 5 b 5 c 5 d 5 e 5 i 5 k 5 m 5 w 67 68 69 6 b 6 c y y y y y 2 with 13 14 18 1 e 1 i 1 k 1 m 1 v 34 38 3 e 3 i 3 k 3 m 3 v 48 4 e 4 i 4 k 4 m 4 v 8 e 8 i 8 k 8 m 8 v ei ek em ev ik im iv km kv mv y y y 3 with 12 14 18 19 1 a 1 e 1 s 1 t 1 x 24 28 29 2 a 2 e 2 s 2 t 2 x 48 49 4 a 4 e 4 s 4 t 4 x 89 8 a 8 e 8 s 8 t 8 x 9 a 9 e 9 s 9 t 9 x ae as at ax es et ex st sx tx y y y 4 with 12 13 18 1 d 1 e 23 28 2 d 2 e 38 3 d 3 e 8 d 8 e ed y y y y y 9 with 13 1 v 1 x 1 y 3 v 3 x 3 y vx vy xy y h with 67 y q with op ow pw y i with 12 y r with uy y 5 with 17 1 b 7 b y y a with 3 y j with xy b with 15 16 56 y y k with 12 1 y 2 y y s with 3 o 3 p 3 y op oy py y l with xy t with 3 w 3 y wy y 8 with 12 13 14 23 24 34 y y y 6 with 17 1 b 1 h 7 b 7 h bh y y y 7 with 15 16 1 h 56 5 h 6 h y y y c with e with 12 13 14 1 y 23 24 2 y 34 3 y 4 y y y y d with 14 y m with 12 y n with xy u with or ox oy rx ry xy y o with qs qu qx qy su sx sy ux uy xy y f with xy p with qs qw sw y v with 29 2 x 2 y 9 x 9 y xy y y W: 1 p 1 q 1 t 1 x 1 y pq pt px py qt qx qy tx ty xy y y x: 39 3 f 3 g 3 j 3 l 3 n 3 o 3 u 3 v 3 w 9 f 9 g 9 j 9 l 9 n 9 o 9 u 9 v 9 w gj gl gn go gu gv gw jl jn jo ju jv jw ln lo lu lv lw no nu nv nw ou ov ow uv uw vw y y: 9 a 9 e 9 f 9 g 9 j 9 k 9 l 9 n 9 o 9 r 9 s 9 t 9 u 9 v 9 w ae af ag aj ak an ao ar as at au av aw ef eg ej ek en eo er es et eu ev ew fg fj fk fn fo fr fs ft fu fv fw gj gk gn go gs gt gu gv gw y y: jk jn jo jr js jt ju jv jw kn ko kr ks kt ku kv kw no nr ns nt nu nv nw or os ot ou ov ow rs rt ru rv rw st su sv sw tu tv tw uv uw vw y y We already know 12348 is a MCLQ 5. What other CLQ 3 s? 12 e 12 i 12 k 12 m 139 13 e 14 d 14 e 157 15 b 167 23 e 34 e 39 x 24 e 348 34 e 16 b 67 h 39 x 3 vy osy pqw ruy tvw osu oux ouy ruy 9 vx 9 vy pqw twy 39 x 9 vx oux 9 vy g with xy

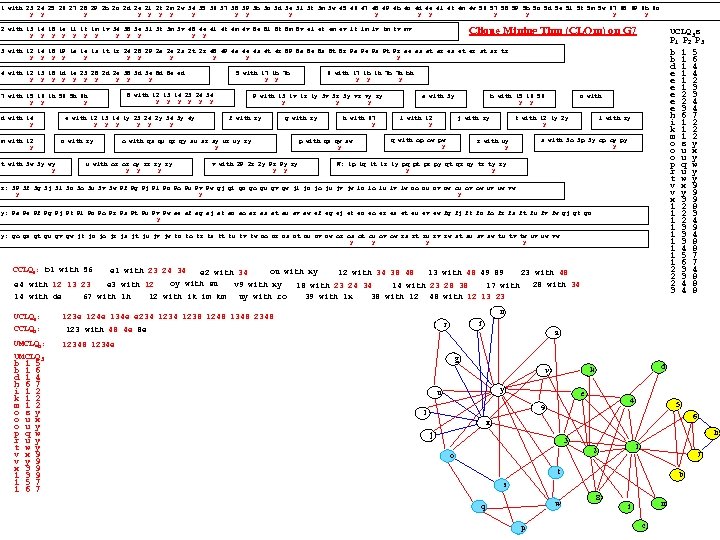1 with 23 24 25 26 27 28 29 2 b 2 c 2 1 with 23 24 25 26 27 28 29 2 b 2 c 2 d 2 e 2 i 2 k 2 m 2 w 34 35 36 37 38 39 3 b 3 c 3 d 3 e 3 i 3 k 3 m 3 w 45 46 47 48 49 4 b 4 c 4 d 4 e 4 i 4 k 4 m 4 w 56 57 58 59 5 b 5 c 5 d 5 e 5 i 5 k 5 m 5 w 67 68 69 6 b 6 c y y y y y Clique Mining Thm (CLQm) on G 7 2 with 13 14 18 1 e 1 i 1 k 1 m 1 v 34 38 3 e 3 i 3 k 3 m 3 v 48 4 e 4 i 4 k 4 m 4 v 8 e 8 i 8 k 8 m 8 v ei ek em ev ik im iv km kv mv y y y UCLQ 3 s p 1 p 2 p 3 3 with 12 14 18 19 1 a 1 e 1 s 1 t 1 x 24 28 29 2 a 2 e 2 s 2 t 2 x 48 49 4 a 4 e 4 s 4 t 4 x 89 8 a 8 e 8 s 8 t 8 x 9 a 9 e 9 s 9 t 9 x ae as at ax es et ex st sx tx y y y 4 with 12 13 18 1 d 1 e 23 28 2 d 2 e 38 3 d 3 e 8 d 8 e ed y y y y y 7 with 15 16 1 h 56 5 h 6 h y y y d with 14 y m with 12 y t with 3 w 3 y wy y 8 with 12 13 14 23 24 34 y y y e with 12 13 14 1 y 23 24 2 y 34 3 y 4 y y y y n with xy 5 with 17 1 b 7 b y y g with xy o with qs qu qx qy su sx sy ux uy xy y u with or ox oy rx ry xy y 6 with 17 1 b 1 h 7 b 7 h bh y y y 9 with 13 1 v 1 x 1 y 3 v 3 x 3 y vx vy xy y f with xy v with 29 2 x 2 y 9 x 9 y xy y y b b d e e e h i k m o o o p r t v v x 1 1 1 1 1 2 2 2 3 h with 67 y p with qs qw sw y a with 3 y i with 12 y b with 15 16 56 y y j with xy q with op ow pw y c with k with 12 1 y 2 y y l with xy s with 3 o 3 p 3 y op oy py y r with uy y W: 1 p 1 q 1 t 1 x 1 y pq pt px py qt qx qy tx ty xy y y x: 39 3 f 3 g 3 j 3 l 3 n 3 o 3 u 3 v 3 w 9 f 9 g 9 j 9 l 9 n 9 o 9 u 9 v 9 w gj gl gn go gu gv gw jl jn jo ju jv jw ln lo lu lv lw no nu nv nw ou ov ow uv uw vw y y: 9 a 9 e 9 f 9 g 9 j 9 k 9 l 9 n 9 o 9 r 9 s 9 t 9 u 9 v 9 w ae af ag aj ak an ao ar as at au av aw ef eg ej ek en eo er es et eu ev ew fg fj fk fn fo fr fs ft fu fv fw gj gk gn y y: go gs gt gu gv gw jk jn jo jr js jt ju jv jw kn ko kr ks kt ku kv kw no nr ns nt nu nv nw or os ot ou ov ow rs rt ru rv rw st su sv sw tu tv tw uv uw vw y y CCLQ 4: b 1 with 56 e 1 with 23 24 34 ou with xy e 2 with 34 12 with 34 38 48 13 with 48 49 89 23 with 48 oy with su v 9 with xy e 4 with 12 13 23 e 3 with 12 28 with 34 14 with 23 28 38 18 with 23 24 34 17 with 14 with de 67 with 1 h 12 with ik im km uy with ro 39 with 1 x 38 with 12 48 with 12 13 23 UCLQ 4: CCLQ 5: 5 6 4 4 2 3 3 4 4 7 2 2 2 y x y w y y 9 9 9 8 3 4 9 4 8 8 7 7 4 8 8 8 n 123 e 124 e 134 e e 234 1238 1248 1348 2348 UMCLQ 5: 1 1 1 2 2 3 6 1 1 1 s u u q u w x y 3 2 2 2 3 3 3 4 5 6 3 3 4 4 12348 1234 e UMCLQ 3 b 1 5 b 1 6 d 1 4 h 6 7 i 1 2 k 1 2 m 1 2 o s y o u x o u y p q w r u y t w y v x 9 v y 9 x 3 9 1 5 7 1 6 7 f r 123 with 48 4 e 8 e a g y u d k v e 4 9 l 5 6 x j h 3 1 2 o 7 t b s w q p 8 m i c

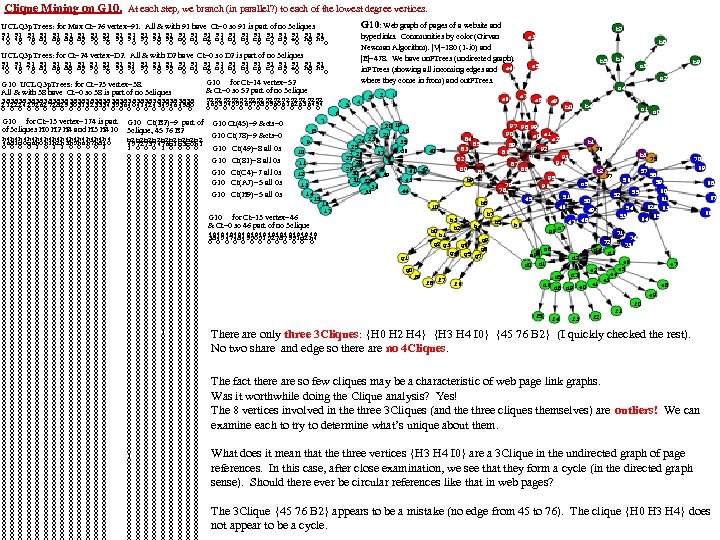Clique Mining on G 10. At each step, we branch (in parallel? ) to Clique Mining on G 10. At each step, we branch (in parallel? ) to each of the lowest degree vertices. UCLQ 3 p. Trees: for Max Ct=26 vertex=91. All & with 91 have Ct=0 so 91 is part of no 3 cliques G 10: Web graph of pages of a website and 91 91 91 91 91 91 91 40 46 76 81 86 88 89 90 92 93 94 97 98 99 a 0 a 1 a 2 a 4 b 1 b 4 c 6 c 7 d 9 e 0 h 8 h 9 0 0 0 0 0 0 0 hyperlinks. Communities by color (Girvan Newman Algorithm). |V|=180 (1 -i 0) and |E|=478. We have un. PTrees (undirected graph). in. PTrees (showing all incoming edges and a 4 where they come in from) and out. PTrees. UCLQ 3 p. Trees: for Ct=24 vertex=D 2. All & with D 2 have Ct=0 so D 2 is part of no 3 cliques 91 91 91 91 91 91 91 40 46 76 81 86 88 89 90 92 93 94 97 98 99 a 0 a 1 a 2 a 4 b 1 b 4 c 6 c 7 d 9 e 0 h 8 h 9 0 0 0 0 0 0 0 G 10 UCLQ 3 p. Trees: for Ct=23 vertex=38. All & with 38 have Ct=0 so 38 is part of no 3 cliques 383838383838383838383838 2122242526272829303132333435364041424345464980 0 0 0 0 0 G 10 for Ct=14 vertex=52 & Ct=0 so 52 part of no 3 clique 52525252525252 4653545556575859606162636494 0 0 0 0 G 10 for Ct=13 vertex=174 is part G 10 Ct(B 2)=9 part of G 10 Ct(45)=9 &cts=0 of 3 cliques H 0 H 2 H 4 and H 3 H 4 I 0 3 clique, 45 76 B 2 G 10 Ct(78)=9 &cts=0 h 4 h 4 h 4 h 4 b 2 b 2 b 2 4681 d 0 g 6 h 0 h 1 h 2 h 3 h 5 h 6 h 7 h 8 i 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 4572737476 b 1 b 3 c 0 h 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 G 10 Ct(49)=8 all 0 s G 10 Ct(81)=8 all 0 s Ct(C 4)=7 all 0 s Ct(A 7)=5 all 0 s Ct(H 9)=5 all 0 s 7 8 9 10 11 12 13 14 15 G 10 for Ct=13 vertex=46 & Ct=0 so 46 part of no 3 clique 5 4 3 2 b 7 a 3 b 8 b 6 b 5 a 5 b 9 c 3 c 2 c 4 1 a 6 a 7 a 8 a 9 b 0 6 20 19 18 22 21 24 23 35 25 36 40 37 26 27 28 38 29 41 42 30 39 43 31 32 34 44 33 16 17 84 83 46464646464646 3845474849505152787991 d 2 h 4 0 0 0 0 80 81 h 9 h 3 h 2 f 8 f 7 57 77 56 50 c 6 c 7 71 72 c 8 c 9 d 4 d 2 d 1 d 5 d 7 69 68 60 61 63 67 66 74 73 d 3 e 2 d 6 d 8 d 9 e 0 e 1 f 6 70 58 59 62 65 64 54 53 49 75 55 52 47 48 h 6 d 0 f 9 b 2 46 h 5 b 3 c 5 h 7 h 4 76 51 45 h 8 c 1 c 0 b 1 95 96 79 78 h 1 g 9 g 2 g 3 g 6 g 8 g 4 g 5 g 7 g 1 g 0 85 82 i 0 h 0 97 98 99 90 a 1 a 2 89 92 86 93 91 94 87 88 b 4 e 3 e 4 e 6 e 5 e 7 e 8 e 9 f 0 f 5 f 4 f 3 f 2 f 1 There are only three 3 Cliques: {H 0 H 2 H 4} {H 3 H 4 I 0} {45 76 B 2} (I quickly checked the rest). No two share and edge so there are no 4 Cliques. The fact there are so few cliques may be a characteristic of web page link graphs. Was it worthwhile doing the Clique analysis? Yes! The 8 vertices involved in the three 3 Cliques (and the three cliques themselves) are outliers! We can examine each to try to determine what’s unique about them. What does it mean that the three vertices {H 3 H 4 I 0} are a 3 Clique in the undirected graph of page references. In this case, after close examination, we see that they form a cycle (in the directed graph sense). Should there ever be circular references like that in web pages? The 3 Clique {45 76 B 2} appears to be a mistake (no edge from 45 to 76). The clique {H 0 H 3 H 4} does not appear to be a cycle.

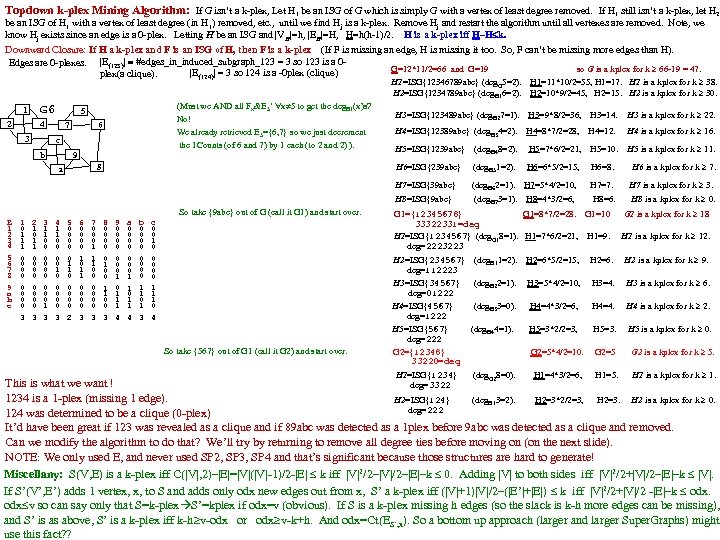Topdown k-plex Mining Algorithm: If G isn’t a k-plex, Let H 1 be an Topdown k-plex Mining Algorithm: If G isn’t a k-plex, Let H 1 be an ISG of G which is simply G with a vertex of least degree removed. If H 1 still isn’t a k-plex, let H 2 be an ISG of H 1 with a vertex of least degree (in H 1) removed, etc. , until we find H j is a k-plex. Remove Hj and restart the algorithm until all vertexes are removed. Note, we know Hj exists since an edge is a 0 -plex. Letting H be an ISG and |VH|=h, |EH|=H, H=h(h-1)/2. H is a k-plex iff H–H k. Downward Closure: If H a k-plex and F is an ISG of H, then F is a k-plex (If F is missing an edge, H is missing it too. So, F can’t be missing more edges than H). Edges are 0 -plexes. |E{123}| #edges_in_induced_subgraph_123 = 3 so 123 is a 0 G=12*11/2=66 and G=19 so G is a kplex for k 66 -19 = 47. |E{124}| = 3 so 124 is a -0 plex (clique) plex(a clique). H 1=ISG{12346789 abc} (deg. G 5=2). H 1=11*10/2=55, H 1=17. H 1 is a kplex for k 38. H 2=ISG{1234789 abc} (deg. H 16=2). H 2=10*9/2=45, H 2=15. H 2 is a kplex for k 30. G 6 1 4 2 3 (Must we AND all Fx&E 5’ x 5 to get the deg. H 1(x)s? No! We already retrieved E 5={6, 7} so we just decrement the 1 Counts (of 6 and 7) by 1 each (to 2 and 2) ). 5 6 7 c 9 b 8 a H 3=ISG{123489 abc} (deg. H 27=1). H 3=9*8/2=36, H 3=14. H 3 is a kplex for k 22. H 4=ISG{12389 abc} (deg. H 34=2). H 4=8*7/2=28, H 4=12. H 4 is a kplex for k 16. H 5=ISG{1239 abc} (deg. H 48=2). H 5=7*6/2=21, H 5=10. H 5 is a kplex for k 11. H 6=ISG{239 abc} (deg. H 51=2). H 6=6*5/2=15, H 6=8. H 6 is a kplex for k 7. H 7=ISG{39 abc} (deg. H 62=1). H 7=5*4/2=10, H 7=7. H 7 is a kplex for k 3. H 8=ISG{9 abc} (deg. H 73=1). H 8=4*3/2=6, H 8=6. H 8 is a kplex for k 0. So take {9 abc} out of G (call it G 1) and start over. E 1 2 3 4 5 6 7 8 9 a b c 1 0 1 1 1 0 0 0 0 3 2 1 0 1 1 0 0 0 0 3 3 1 1 0 0 0 0 0 1 3 4 1 1 0 0 0 0 0 3 5 0 0 0 1 1 0 0 0 2 6 0 0 1 0 1 1 0 0 3 7 0 0 0 1 1 1 0 0 0 3 8 0 0 0 1 1 0 0 3 9 0 0 0 0 1 1 1 4 a 0 0 0 0 1 1 4 b 0 0 0 0 1 1 0 1 3 c 0 0 1 0 0 0 1 1 1 0 4 So take {567} out of G 1 (call it G 2) and start over. G 1={12345678} G 1=8*7/2=28. G 1=10 G 1 is a kplex for k 18 33322331=deg H 1=ISG{1234567} (deg. G 18=1). H 1=7*6/2=21, H 1=9. H 1 is a kplex for k 12. deg=2223223 H 2=ISG{234567} (deg. H 11=2). H 2=6*5/2=15, H 2=6. H 2 is a kplex for k 9. deg=112223 H 3=ISG{34567} (deg. H 22=1). H 3=5*4/2=10, H 3=4. H 3 is a kplex for k 6. deg=01222 H 4=ISG{4567} (deg. H 33=0). H 4=4*3/2=6, H 4=4. H 4 is a kplex for k 2. deg=1222 H 5=ISG{567} (deg. H 44=1). H 5=3*2/2=3, H 5=3. H 5 is a kplex for k 0. deg=222 G 2={12348} G 2=5*4/2=10. G 2=5 G 2 is a kplex for k 5. 33220=deg H 1=ISG{1234} (deg. G 28=0). H 1=4*3/2=6, H 1=5. H 1 is a kplex for k 1. This is what we want ! deg=3322 1234 is a 1 -plex (missing 1 edge). H 2=ISG{124} (deg. H 13=2). H 2=3*2/2=3, H 2=3. H 2 is a kplex for k 0. deg=222 124 was determined to be a clique (0 -plex) It’d have been great if 123 was revealed as a clique and if 89 abc was detected as a 1 plex before 9 abc was detected as a clique and removed. Can we modify the algorithm to do that? We’ll try by returning to remove all degree ties before moving on (on the next slide). NOTE: We only used E, and never used SP 2, SP 3, SP 4 and that’s significant because those structures are hard to generate! Miscellany: S(V, E) is a k-plex iff C(|V|, 2)–|E|=|V|(|V|-1)/2 -|E| k iff |V|2/2–|V|/2–|E|–k 0. Adding |V| to both sides iff |V|2/2+|V|/2–|E|–k |V|. If S’(V’, E’) adds 1 vertex, x, to S and adds only odx new edges out from x, S’ a k-plex iff (|V|+1)|V|/2–(|E’|+|E|) k iff |V|2/2+|V|/2 -|E|–k odx v so can say only that S=k-plex S’=kplex if odx=v (obvious). If S is a k-plex missing h edges (so the slack is k-h more edges can be missing), and S’ is as above, S’ is a k-plex iff k-h v-odx or odx v-k+h. And odx=Ct(ES’, x). So a bottom up approach (larger and larger Super. Graphs) might use this fact? ?

Topdown k-plex k-core Mining Alg If G isn’t a k-plex, Let H 1 be Topdown k-plex k-core Mining Alg If G isn’t a k-plex, Let H 1 be an ISG of G with a vertex of least degree removed. In parallel remove all degree ties before moving on. If H 1 still isn’t a k-plex, let H 2 be an ISG of H 1 with a vertex of least degree (in H 1) removed, etc. , until we find H j is a k-plex (usually our interest is in k=0). Remove H j and restart the alg until all vertexes are removed. Note, we know H j exists since an edge is a 0 -plex. H an ISG and |VH|=h, |EH|=H, H=h(h-1)/2. H is a k-plex iff H–H k. Downward Closure: If H a k-plex and F is an ISG of H, then F is a k-plex (If F is missing an edge, H is missing it too. So, F can’t be missing more edges than H). A k-core is a Subgraph containing k edges. 1 G 6 5 4 2 3 E 1 2 3 4 5 6 7 8 9 a b c 6 7 c 9 b a 8 {123456789 abc} 47 plex 19 core 333323334434 {1234 6789 abc} 37 plex 17 core 3333 2234434 1 0 1 1 1 0 0 0 0 3 2 1 0 1 1 0 0 0 0 3 3 1 1 0 0 0 0 0 1 3 4 1 1 0 0 0 0 0 3 5 0 0 0 1 1 0 0 0 2 A COMBO(|V|, 2)-core is a clique. Upward Closure of k-cores: If H is a kcore and H is an ISG of F, then F is a kcore. 6 0 0 1 0 1 1 0 0 3 7 0 0 0 1 1 1 0 0 0 3 8 0 0 0 1 1 0 0 3 9 0 0 0 0 1 1 1 4 a 0 0 0 0 1 1 4 b 0 0 0 0 1 1 0 1 3 c 0 0 1 0 0 0 1 1 1 0 4 Topdown Mining all kplexes and kcores. At each step, we [potentially] branch to each of the lowest degree vertices. {1234 6 89 abc} 30 plex 15 core 3332 1 34434 {1234 3333 789 abc} 30 plex 15 core 124434 {1234 3332 89 abc} 22 plex 14 core 24434 same as stop {123 223 89 abc} 16 plex 12 core 24434 {1234 3332 9 abc} 16 plex 12 core 3334 { 23 12 89 abc} 11 plex 10 core 24434 {1 3 1 2 89 abc} 11 plex 10 core 24434 {123 223 9 abc} 11 plex 10 core 3334 same as stop { 89 abc} 6 plex 9 core 24434 { 3 1 89 abc} 6 plex 9 core 24434 same as stop { 23 12 9 abc} 7 plex 8 core 3334 {1 3 1 2 9 abc} 7 plex 8 core 3334 { 89 abc} 2 plex 8 core 24433 { 9 abc} 3 plex 7 core 3334 { 3 1 9 abc} 3 plex 7 core 3334 same as stop { 9 abc} 0 plex 6 core 3333 { 9 abc} 0 plex 6 core 3333 3 1 So take {9 abc} and start over. {12345678} 18 plex 10 core 33232331 {1234567} 12 plex 9 core 3323223 {12 4567} 12 plex 9 core 22 3223 { 2 4567} 5 plex 5 core 1 2223 {1 1 4567} 5 plex 5 core 2223 {12 4 67} 5 plex 5 core 22 3 12 {12 45 7} 5 plex 5 core 22 31 2 {1234 3323 7} 4 plex 6 core 1 { 4567} 2 plex 4 core 1223 same as stop {12 4 22 3 7} 2 plex 4 core 1 {12 4 22 3 {1234 3322 } 1 plex 5 core { 567} 0 plex 3 core 222 {12 4 22 2 } 0 plex 3 core {1234 67} 8 plex 7 core 3323 12 7} 2 plex 4 core 1 same as stop {12 4 } 0 plex 3 core 22 2 same as stop {12345 7} 8 plex 7 core 33231 2 {1234 3323 7} 4 plex 6 core 1 same as stop {123 222 } 0 plex 3 core

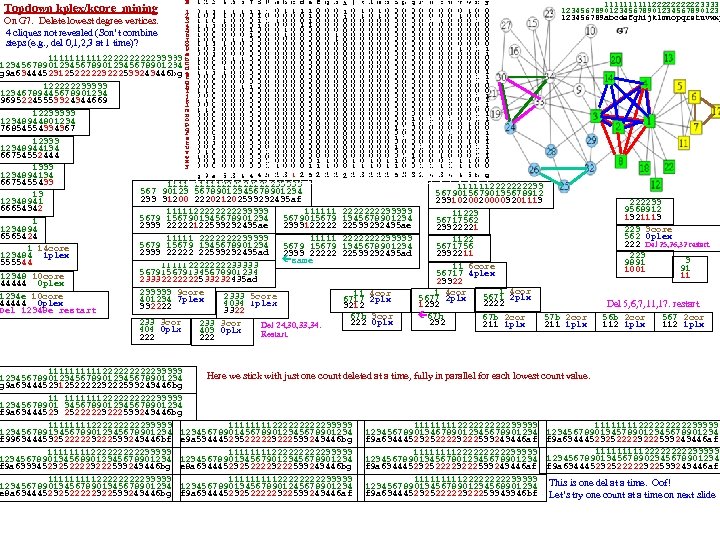Topdown kplex/kcore mining On G 7. Delete lowest degree vertices. 4 cliques not revealed Topdown kplex/kcore mining On G 7. Delete lowest degree vertices. 4 cliques not revealed (Son’t combine steps (e. g. , del 0, 1, 2, 3 at 1 time)? 111112222233333 123456789012345678901234 g 9 a 63444523125222223222533243446 bg 122222233333 12346789445678901234 96952245553324344669 12233333 12348944801234 76854554334367 12333 12348944134 66754552444 1333 1234894134 6675455433 13 12348941 66654342 1 1234894 6565424 1 14 core 123484 1 plex 555544 12348 10 core 44444 0 plex 1234 e 10 core 44444 0 plex Del 12348 e restart E 1 2 3 4 5 6 7 8 9 a b c d e f g h I j k l m n o p q r s t u v w x y 1 0 1 1 1 1 0 0 0 1 0 1 0 0 0 0 0 1 0 0 g 2 1 0 1 1 0 0 0 0 0 1 0 0 0 9 3 1 1 0 0 0 1 1 1 0 0 0 0 1 1 0 0 0 1 0 a 4 1 1 1 0 0 0 0 0 0 0 6 5 1 0 0 0 0 0 0 0 0 3 6 1 0 0 0 0 0 0 0 0 0 0 4 7 1 0 0 0 1 1 0 0 0 0 0 0 0 4 8 1 1 0 0 0 0 0 0 0 0 4 9 1 0 0 0 0 0 0 0 1 0 1 1 5 a 0 0 1 0 0 0 0 0 0 0 0 1 2 b 1 0 0 0 1 1 0 0 0 0 0 0 0 3 c 1 0 0 0 0 0 0 0 0 0 1 d 1 0 0 0 0 0 0 0 0 2 e 1 1 0 0 0 0 0 0 0 0 1 5 f 0 0 0 0 0 0 0 0 1 1 2 g 0 0 0 0 0 0 0 0 1 1 2 h 0 0 0 1 1 0 0 0 0 0 0 0 2 111112222233333 567 90123 5678901234 233 31200 222021202533232435 af 111112222233333 111111 5679 1567901345678901234 5679015679 2333 22222122533232435 ae 2333122222 11111 222233333 11111 5679 1345678901234 5679 15679 2333 22222 22533232435 ad 2333 22222 same 11111222233333 56791345678901234 23332222222533232435 ad 233333 9 core 2333 5 core 401234 7 plex 4034 1 plex 332222 3322 233 3 cor Del 24, 30, 33, 34. 404 0 plx 403 0 plx Restart. 222 i 1 1 0 0 0 0 0 0 0 0 2 j 0 0 0 0 0 0 0 0 1 1 2 l 0 0 0 0 0 0 0 0 1 1 2 k 1 1 0 0 0 0 0 0 0 0 1 3 m 1 1 0 0 0 0 0 0 0 0 2 n 0 0 0 0 0 0 0 0 1 1 2 o 0 0 0 0 0 0 0 1 0 1 0 0 1 1 5 p 0 0 0 0 0 0 0 1 0 0 3 q 0 0 0 0 0 0 1 1 0 0 0 1 0 0 3 222233333 1345678901234 22533232435 ae 222233333 1345678901234 22533232435 ad 11 6717 3212 67 h 222 4 cor 2 plx 3 cor 0 plx r 0 0 0 0 0 0 0 0 1 0 0 0 1 2 s 0 0 1 0 0 0 0 0 1 1 0 0 0 0 1 4 t 0 0 1 0 0 0 0 0 0 0 1 0 1 3 u 0 0 0 0 0 0 1 0 0 0 1 1 4 v 0 1 0 0 0 0 0 0 0 1 1 4 w 1 0 0 0 0 0 0 1 1 0 0 0 1 1 6 x 0 0 1 0 0 0 0 0 1 1 0 0 1 0 1 1 0 0 0 1 1 1 0 0 b y 0 0 0 0 1 1 1 0 1 1 0 0 1 1 1 0 0 g 111112222233333 12345678901234567890123456789 abcdefghijklmnopqrstuvwxy 111111222233 56790135678912 23310200200003201113 11223 56717562 23322221 1122 5671756 2332211 11 6 core 56717 4 plex 23322 1 4 cor 5671 2 plx 5677 2 plx 2222 1232 67 h 67 b 2 cor 57 b 2 cor 232 211 1 plx 222233 9568912 1321113 223 3 core 562 0 plex 222 Del 25, 26, 32 restart 223 3 9891 91 1001 11 Del 5, 6, 7, 11, 17. restart. 56 b 2 cor 112 1 plx 567 2 cor 112 1 plx 111112222233333 Here we stick with just one count deleted at a time, fully in parallel for each lowest count value. 123456789012345678901234 g 9 a 63444523125222223222533243446 bg 11 11111112222233333 12345678901234 f 9 a 63444523 25222223222533243446 bg 11111111222222222233333 12345678913456789012345678901234567890123456789013467890123456789012345678901345789012345678901234 f 99634445325222223222533243446 bf e 9 a 534445235222223222533243446 bg f 9 a 634445232522223222533243446 af 1111122222222233333 1111111122222233333 11112222233333 1234567890134568901234567890123456789013456780123456789012345678901345678902345678901234 f 9 a 633345232522223222533243446 bg e 8 a 634445232522223222533243446 bg f 9 a 634445232522223222533243446 af f 9 a 634445232522222322533243446 af 11111111122222222233333 123456789013456789012345678901245678901234 e 8 a 634445232522222322533243446 bg f 9 a 634445232522222322533243446 af 111112222233333 12345678901234568901234 f 9 a 634445232522222322253343346 bf This is one del at a time. Oof! Let’s try one count at a time on next slide

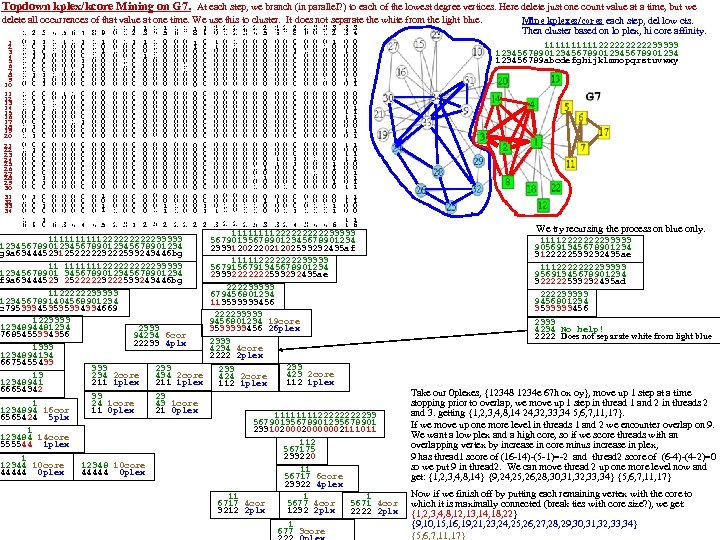Topdown kplex/kcore Mining on G 7. At each step, we branch (in parallel? ) Topdown kplex/kcore Mining on G 7. At each step, we branch (in parallel? ) to each of the lowest degree vertices. Here delete just one count value at a time, but we delete all occurrences of that value at one time. We use this to cluster. It does not separate the white from the light blue. 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 1 0 1 1 1 1 0 0 0 1 0 1 0 0 0 0 0 1 6 2 1 0 1 1 0 0 0 0 0 1 0 0 0 3 1 1 0 0 0 1 1 1 0 0 0 0 1 1 0 0 0 1 9 0 4 1 1 1 0 0 0 0 0 0 0 5 1 0 0 0 0 0 0 0 0 6 1 0 0 0 0 0 0 0 0 0 0 7 1 0 0 0 1 1 0 0 0 0 0 0 0 6 3 4 4 8 1 1 0 0 0 0 0 0 0 0 9 1 0 0 0 0 0 0 0 1 0 1 1 4 5 1 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 1 2 1 0 0 0 0 0 0 0 0 0 1 3 1 0 0 0 0 0 0 0 0 1 4 1 1 0 0 0 0 0 0 0 0 1 1 5 0 0 0 0 0 0 0 0 1 1 1 6 0 0 0 0 0 0 0 0 1 1 1 7 0 0 0 1 1 0 0 0 0 0 0 0 1 8 1 1 0 0 0 0 0 0 0 0 1 9 0 0 0 0 0 0 0 0 1 1 2 0 1 1 0 0 0 0 0 0 0 0 1 2 1 0 0 0 0 0 0 0 0 1 1 2 2 1 1 0 0 0 0 0 0 0 0 2 3 0 0 0 0 0 0 0 0 1 1 2 4 0 0 0 0 0 0 0 1 0 1 0 0 1 1 2 5 0 0 0 0 0 0 0 1 0 0 2 3 1 2 5 2 2 2 3 2 2 2 5 3 2 6 0 0 0 0 0 0 1 1 0 0 0 1 0 0 2 7 0 0 0 0 0 0 0 0 1 0 0 0 1 2 8 0 0 1 0 0 0 0 0 1 1 0 0 0 0 1 3 2 4 2 9 0 0 1 0 0 0 0 0 0 0 1 0 1 3 0 0 0 0 0 0 1 0 0 0 0 0 1 1 3 1 0 0 0 0 0 0 0 0 1 1 3 2 1 0 0 0 0 0 0 1 1 0 0 0 1 1 3 4 4 6 3 3 0 0 1 0 0 0 0 0 1 1 0 0 1 0 1 1 0 0 0 1 1 1 0 0 1 1 3 4 0 0 0 0 1 1 1 0 1 1 0 0 1 6 11112222233333 111112222233333 5679013567890123456789012345678901234 2333120222021202533232435 af g 9 a 63444523125222223222533243446 bg 11111222233333 11 11111112222233333 567913456789012345678901 345678901234 23332222222533232435 ae f 9 a 63444523 25222223222533243446 bg 222233333 1122222233333 679456801234567891404568901234 113533333456 c 795333453535334334669 222233333 1223333 9456801234 19 core 1234894481234 2333 3533333456 26 plex 7685455334356 94234 6 cor 2333 22233 4 plx 1333 4234 4 core 1234894134 2222 2 plex 6675455433 233 333 233 423 2 core 13 234 2 core 424 2 core 112 1 plex 12348941 211 1 plex 112 1 plex 66654342 33 23 1 24 1 core 43 1 core 1234894 16 cor 11 0 plex 21 0 plex 11112222233 6565424 5 plx 56790135678901235678901 2331020000002111011 1 123484 14 core 112 555544 1 plex 567175 233220 1 12344 10 core 12348 10 core 11 44444 0 plex 56717 6 core 23322 4 plex 11 1 1 6717 4 cor 5671 4 cor 3212 2 plx 1232 2 plx 2222 2 plx 1 677 3 core Mine kplexes/cores each step, del low cts. Then cluster based on lo plex, hi core affinity. 111112222233333 12345678901234567890123456789 abcdefghijklmnopqrstuvwxy We try recursing the process on blue only. 1111222233333 905691345678901234 3122222533232435 ae 111222233333 95691345678901234 322222533232435 ad 222233333 9456801234 3533333456 2333 4234 No help! 2222 Does not separate white from light blue Take our 0 plexes, {12348 1234 e 67 h ox oy}, move up 1 step at a time stopping prior to overlap, we move up 1 step in thread 1 and 2 in threads 2 and 3. getting {1, 2, 3, 4, 8, 14 24, 32, 33, 34 5, 6, 7, 11, 17}. If we move up one more level in threads 1 and 2 we encounter overlap on 9. We want a low plex and a high core, so if we score threads with an overlapping vertex by increase in core minus increase in plex, 9 has thread 1 score of (16 -14)-(5 -1)=-2 and thread 2 score of (6 -4)-(4 -2)=0 so we put 9 in thread 2. We can move thread 2 up one more level now and get: {1, 2, 3, 4, 8, 14} {9, 24, 25, 26, 28, 30, 31, 32, 33, 34} {5, 6, 7, 11, 17} Now if we finish off by putting each remaining vertex with the core to which it is maximally connected (break ties with core size? ), we get: {1, 2, 3, 4, 8, 12, 13, 14, 18, 22} {9, 10, 15, 16, 19, 21, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34} {5, 6, 7, 11, 17}

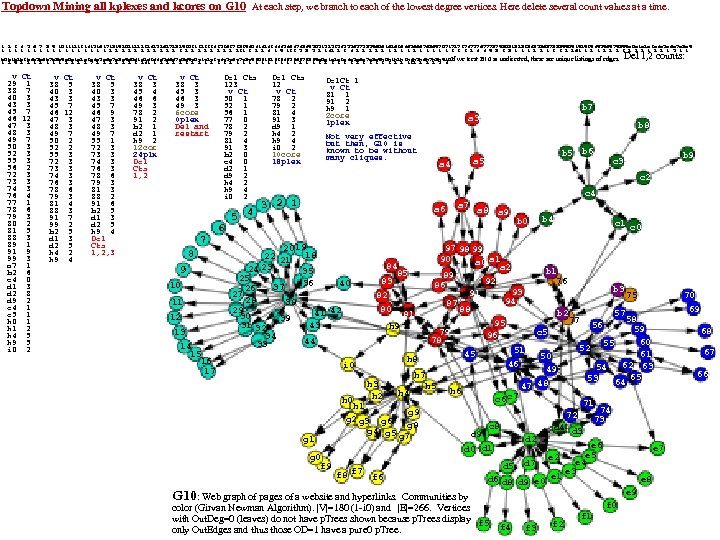Topdown Mining all kplexes and kcores on G 10 At each step, we branch Topdown Mining all kplexes and kcores on G 10 At each step, we branch to each of the lowest degree vertices. Here delete several count values at a time. 1 2 3 4 5 6 7 8 9 101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899 a 0 a 1 a 2 a 3 a 4 a 5 a 6 a 7 a 8 a 9 1 1 1 1 1 2 2 2 3 2 2 2 2 231 3 2 2 4 1 9 133 5 8 5 2 142 2 3 4 2 2 2 1 1 1 3 3 3 2 4 4 9 8 3 8 1 1 1 2 2 1 3 3 2 261 1 2 2 2 3 2 2 2 1 5 1 1 Del 1, 2 counts: b 0 b 1 b 2 b 3 b 4 b 5 b 6 b 7 b 8 b 9 c 0 c 1 c 2 c 3 c 4 c 5 c 6 c 7 c 8 c 9 d 0 d 1 d 2 d 3 d 4 d 5 d 6 d 7 d 8 d 9 e 0 e 1 e 2 e 3 e 4 e 5 e 6 e 7 e 8 e 9 f 0 f 1 f 2 f 3 f 4 f 5 f 6 f 7 f 8 f 9 g 0 g 1 g 2 g 3 g 4 g 5 g 6 g 7 g 8 g 9 h 0 h 1 h 2 h 3 h 4 h 5 h 6 h 7 h 8 h 9 i 0 If we treat B 10 as undirected, these are unique listings of edges. 1 2 9 2 2 1 1 1 2 2 7 2 2 2 3 241 1 2 2 3 2 2 1 2 3 3 2 1 1 1 1 1 2 1 1 1 3 3 2 2 132 2 5 4 v Ct 29 1 38 7 40 3 43 3 45 7 46 12 47 3 48 3 49 7 50 3 52 3 55 3 56 2 72 3 73 3 74 3 76 4 77 1 78 6 79 3 80 2 81 5 88 3 89 1 91 9 99 3 a 7 1 b 2 6 c 4 0 d 1 3 d 2 8 d 9 2 e 4 1 e 5 1 h 0 1 h 1 2 h 4 5 h 9 5 i 0 2 v Ct 38 5 40 3 43 3 45 7 46 12 47 3 48 3 49 7 50 2 52 2 55 3 72 3 73 3 74 3 76 3 78 6 79 3 81 4 88 3 91 7 99 2 b 2 5 d 1 3 d 2 5 h 4 2 h 9 4 v Ct 38 5 40 3 43 3 45 7 46 9 47 3 48 3 49 7 55 1 72 3 73 3 74 3 76 3 78 6 79 3 81 3 88 2 91 6 b 2 5 d 1 3 d 2 5 h 9 4 Del Cts 1, 2, 3 v Ct 38 3 45 4 46 6 49 3 78 2 91 2 b 2 1 d 2 1 h 9 2 12 cor 24 plx Del Cts 1, 2 v Ct 38 3 45 3 46 3 49 3 6 core 0 plex Del and restart Del Cts 123 v Ct 50 1 52 1 56 1 77 0 78 2 79 2 81 4 91 3 b 2 0 c 4 0 d 2 1 d 9 2 h 4 2 h 9 4 i 0 2 6 7 8 9 10 11 12 13 14 15 16 17 5 4 Del Cts 12 v Ct 78 2 79 2 81 4 91 3 d 9 1 h 4 2 h 9 4 i 0 2 10 core 18 plex Del. Ct 1 v Ct 81 1 91 2 h 9 1 2 core 1 plex b 7 a 3 Not very effective but then, G 10 is known to be without many cliques. b 8 b 6 b 5 a 4 b 9 c 3 c 2 c 4 3 2 1 a 6 20 19 18 22 21 23 24 35 25 36 40 37 26 27 28 38 29 41 42 30 39 43 31 32 34 44 33 84 85 83 82 80 h 9 h 8 i 0 h 0 g 1 g 0 f 9 81 h 3 h 2 h 4 a 7 a 8 a 9 97 98 99 90 a 1 a 2 89 92 86 93 91 94 87 88 95 79 96 78 51 45 h 7 h 5 46 h 6 c 7 h 1 g 9 g 2 g 3 g 6 g 8 g 4 g 5 g 7 b 4 c 1 c 0 b 1 76 b 2 b 3 c 9 58 59 60 55 52 61 62 63 54 65 53 64 c 5 50 49 48 47 56 71 c 8 d 4 d 2 d 5 f 6 G 10: Web graph of pages of a website and hyperlinks. Communities by d 7 e 2 d 6 d 8 d 9 e 0 e 1 color (Girvan Newman Algorithm). |V|=180 (1 -i 0) and |E|=266. Vertices with Out. Deg=0 (leaves) do not have p. Trees shown because p. Trees display f 5 only Out. Edges and thus those OD=1 have a pure 0 p. Tree. 74 73 d 3 e 6 e 5 e 4 e 3 e 7 e 8 e 9 f 0 f 4 75 57 77 72 d 0 d 1 f 8 f 7 b 0 f 3 f 2 f 1 70 69 68 67 66

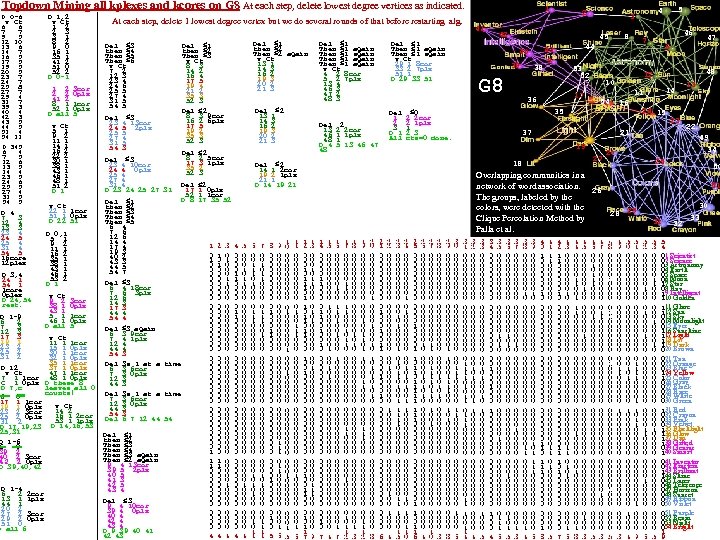Topdown Mining all kplexes and kcores on G 8 At each step, delete lowest Topdown Mining all kplexes and kcores on G 8 At each step, delete lowest degree vertices as indicated. D 0 -6 v Ct 6 6 7 7 9 5 12 10 13 6 14 7 16 5 17 5 19 5 20 5 23 7 24 7 25 8 27 7 29 4 31 7 39 3 40 4 42 3 43 5 44 5 51 4 54 11 D 345 6 4 7 5 12 6 13 5 14 4 23 5 24 6 25 5 27 4 31 5 54 5 D 4 7 3 12 4 13 3 23 4 24 5 25 4 31 4 54 5 16 core 12 plex D 3, 4 24 1 54 1 1 core 0 plex D 24, 54 rest. D 1 -9 6 2 7 3 12 3 17 3 19 1 23 2 25 2 31 2 D 1, 2 v Ct 1 2 2 3 3 1 8 2 9 0 16 1 35 1 41 2 51 0 52 2 D 0 -1 1 2 2 2 41 2 8 1 52 1 D all At each step, delete 1 lowest degree vertex but we do several rounds of that before restarting alg. 3 cor 0 plx 1 cor 0 plx 5 v Ct 5 1 9 2 11 1 14 1 16 2 22 2 30 1 38 1 43 1 46 1 48 1 51 2 D 1 D 0, 1 5 1 9 2 11 1 16 2 35 1 38 1 43 1 46 1 53 2 D 1 3 cor 0 plx 1 cor 0 plx 5 v Ct 11 1 1 cor 15 1 0 plx 30 1 1 cor 32 1 0 plx 35 1 1 cor 37 1 0 plx D 12 47 1 1 cor v Ct 48 1 0 plx 7 1 1 cor C 1 0 plx D these 8 leaves all 0 D 7, c counts! 6 0 17 1 1 cor v Ct 19 1 0 plx 14 2 23 2 3 cor 16 1 2 cor 25 2 0 plx 53 1 1 plx 31 2 D 14, 16, 53 D 17, 19, 23 25, 31 D 1 -6 6 0 39 2 40 2 3 cor 42 2 0 plx D 39, 40, 42 D 1 -4 6 2 2 cor 13 1 1 plx 44 1 20 2 27 2 3 cor 29 2 0 plx 51 0 D all 6 Del 23 24 25 27 31 54 3 4 13 cor 5 2 plx 5 4 5 3 Del 3 23 4 10 cor 24 4 0 plx 25 4 27 4 31 4 D 23 24 25 27 31 v Ct 22 1 1 cor 51 1 0 plx D 22 51 v Ct 9 2 38 1 43 1 5 1 46 1 D all Del 3 then 4 Then 5 Then 6 v Ct 7 2 12 3 23 4 24 6 25 5 27 4 31 5 54 5 Del 1 then 2 Then 3 Then 4 Then 5 6 4 7 6 12 6 14 4 17 4 19 3 40 2 43 3 44 5 54 7 Del 6 7 12 14 17 44 54 3 4 18 cor 6 3 plx 6 3 3 4 4 Del 6 7 12 44 54 Del 6 7 12 44 Del 7 12 44 54 Del 3 again 3 9 cor 4 1 plx 4 4 3 3 s 1 at a time 3 6 cor 3 0 plx 3 3 6 7 12 44 54 Del 1 then 2 Then 3 Then 4 Then 3 again Then 2 again 9 4 13 cor 39 5 2 plx 40 5 41 3 42 5 43 4 Del 3 9 4 10 cor 39 4 0 plx 40 4 42 4 43 4 D 9 39 40 41 42 43 Del 1 then 2 Then 2 again v Ct 13 1 14 3 16 2 19 3 20 2 21 3 Del 1 then 2 Then 3 v Ct 8 3 14 2 16 4 17 5 19 4 21 2 35 3 52 3 Del 2 8 3 9 cor 16 2 6 plx 17 5 19 2 35 3 52 3 Del 13 14 16 19 20 21 Del 8 17 35 52 2 2 5 cor 3 1 plx 2 3 Del 17 52 D 8 2 1 0 plx 1 1 cor 17 35 52 1 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 4 2 1 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 4 3 0 1 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 4 1 3 2 3 Del 1 Then 1 again Then 1 sgain Then 1 again v Ct 4 2 8 cor 5 2 7 plx 13 4 46 3 47 2 48 3 41 Del 1 Then 1 again Then 1 sgain v Ct 29 1 8 cor 33 2 7 plx 51 1 D 29 33 51 2 Del 13 46 48 D 4 48 1 Del 1 2 3 D 1 All 2 2 2 cor 1 1 plx 1 5 13 46 47 5 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 4 6 0 0 1 1 1 0 0 0 0 0 0 0 0 0 1 0 1 0 1 1 7 0 0 1 1 0 0 0 1 1 1 0 0 0 0 0 0 0 1 0 0 0 0 1 1 8 0 0 0 1 0 0 0 1 1 0 0 0 0 0 0 0 1 0 0 0 1 0 0 5 9 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 1 6 1 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 5 1 1 0 0 0 1 0 0 1 1 1 0 0 0 0 0 0 0 1 0 0 0 0 0 1 6 8 45 39 38 G 8 53 52 0 2 2 cor 2 1 plx 1 2 3 cts=0 done. 16 37 1 4 0 0 0 1 1 0 0 1 0 0 0 0 0 0 0 0 0 1 0 7 1 5 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 4 1 6 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 1 7 0 0 0 1 1 0 0 0 0 1 1 0 0 0 0 1 0 1 1 2 1 8 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 3 1 9 0 0 0 0 1 0 0 1 1 0 0 0 0 1 1 1 0 0 0 0 1 1 1 2 2 0 0 0 0 0 1 0 0 0 1 0 1 0 1 0 0 0 0 0 0 0 8 19 2 1 0 0 0 1 0 0 1 0 0 0 0 0 0 0 6 2 2 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 4 2 3 0 0 0 1 0 0 0 0 1 0 1 1 0 0 1 1 1 0 0 0 0 1 1 1 0 0 0 1 5 2 4 0 0 0 0 0 1 0 1 0 1 0 0 1 1 0 0 0 0 0 1 0 0 1 1 0 2 5 0 0 0 0 1 0 0 1 1 1 1 0 0 0 0 1 1 0 0 1 1 6 2 6 0 0 0 0 0 1 0 0 0 1 0 1 0 0 0 0 0 0 0 4 2 7 0 0 0 0 0 1 1 0 1 1 0 0 0 0 0 0 1 0 2 8 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 3 2 9 0 0 0 0 0 1 1 0 0 0 1 1 0 0 0 0 0 0 0 8 3 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 1 0 0 0 6 3 1 0 0 0 0 0 0 1 1 0 1 1 1 0 0 0 0 1 1 1 0 0 1 1 4 3 2 0 0 0 0 0 0 1 0 0 0 0 1 1 0 0 0 0 0 0 4 3 3 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 1 0 0 0 5 3 4 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 4 3 5 0 0 0 0 0 0 0 0 1 0 0 0 0 1 1 1 6 3 6 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 1 5 3 7 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 3 27 3 8 0 0 0 0 1 0 0 0 0 0 0 0 0 1 1 0 0 0 0 1 4 3 9 0 0 0 0 1 0 0 0 0 0 0 0 1 0 1 1 0 0 0 6 23 21 4 0 1 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 1 8 4 1 1 1 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 5 4 2 1 1 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 7 4 3 0 0 0 0 1 0 0 0 0 0 0 0 0 1 1 0 1 0 0 0 0 0 1 6 4 4 0 0 0 1 1 1 0 0 0 0 0 0 1 0 0 0 0 1 8 4 5 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 3 4 6 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 5 4 7 0 0 0 1 1 0 0 0 0 0 0 0 0 0 1 0 0 0 3 13 22 49 34 20 25 Overlapping communities in a network of word association. 26 The groups, labeled by the colors, were detected with the 28 29 Clique Percolation Method by Palla et al. 1 3 0 0 0 1 1 0 0 0 0 0 1 0 0 0 0 0 0 1 1 1 0 0 0 9 14 24 15 35 18 1 2 0 0 0 1 1 1 0 0 0 1 0 0 0 0 0 1 0 0 1 1 0 0 0 1 1 7 48 11 54 47 6 12 10 17 36 46 7 44 43 9 5 4 3 42 40 Del 2 14 1 2 cor 19 2 1 plx 21 1 D 14 19 21 4 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 4 2 4 8 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 1 0 0 0 0 5 4 9 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 3 5 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 4 5 1 0 0 0 0 0 0 1 1 0 0 0 0 0 1 0 0 9 50 51 31 5 2 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 0 0 6 5 3 0 0 0 1 1 0 0 0 0 0 0 0 1 0 0 0 0 0 5 32 30 33 5 4 01 Scientist 02 Science 03 Astronomy 04 Earth 05 Space 06 Moon 17 Star 08 Ray 19 Intelligent 110 Golden 111 Glare 112 Sun 013 Sky 014 Moonlight 015 Eyes 116 Sunshine 117 Light 118 Lit 119 Dark 020 Brown 021 Tan 022 Orange 023 Blue 124 Yellow 125 Color 026 Gray 027 Black 028 Race 029 White 030 Green 131 Red 032 Crayon 033 Pink 034 Velvet 135 Flashlight 136 Glow 137 Dim 138 Gifted 039 Genius 140 Smart 041 Inventor 042 Einstein 143 Brilliant 144 Shine 045 Laser 046 Telescope 047 Horizon 048 Sunset 049 Ribbon 050 Violet 051 Purple 052 Beam 053 Night 054 Bright 1 9

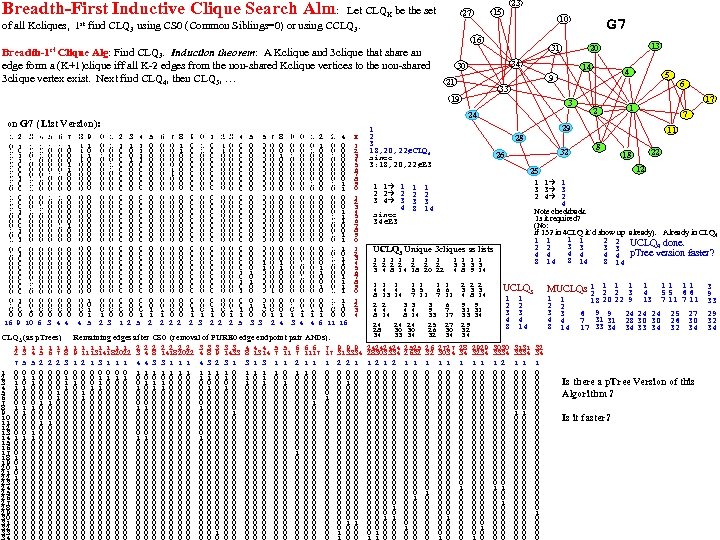Breadth-First Inductive Clique Search Alm: Let CLQK be the set 23 15 27 10 Breadth-First Inductive Clique Search Alm: Let CLQK be the set 23 15 27 10 of all Kcliques, 1 st find CLQ 3 using CS 0 (Common Siblings=0) or using CCLQ 3. 16 Breadth-1 st Clique Alg: Find CLQ 3. Induction theorem: A Kclique and 3 clique that share an edge form a (K+1)clique iff all K-2 edges from the non-shared Kclique vertices to the non-shared 3 clique vertex exist. Next find CLQ 4, then CLQ 5, … 34 2 1 0 1 1 0 0 0 0 0 1 0 0 0 9 3 1 1 0 0 0 1 1 1 0 0 0 0 1 1 0 0 0 10 4 1 1 1 0 0 0 0 0 0 0 6 5 1 0 0 0 0 0 0 0 0 3 6 1 0 0 0 0 0 0 0 0 0 0 4 7 8 1 1 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 4 4 CLQ 3 (as p. Trees) 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 1 2 7 0 0 1 1 0 0 0 0 0 1 0 1 0 0 0 1 3 5 0 1 0 0 0 1 1 0 0 0 0 0 0 1 4 5 0 1 1 0 0 0 0 0 0 0 1 5 2 0 0 0 1 0 0 0 0 0 0 0 1 6 2 0 0 0 1 0 0 0 0 0 0 0 1 7 2 0 0 1 1 0 0 0 0 0 0 0 9 1 0 0 0 0 0 0 0 1 0 1 1 5 0 0 0 1 0 0 0 0 0 0 0 0 1 2 1 1 0 0 0 0 0 0 0 0 3 2 1 0 0 0 0 0 0 0 0 0 1 3 1 0 0 0 0 0 0 0 0 2 4 1 1 0 0 0 0 0 0 0 0 1 5 5 0 0 0 0 0 0 0 0 1 1 2 6 0 0 0 0 0 0 0 0 1 1 2 7 0 0 0 1 1 0 0 0 0 0 0 0 2 8 1 1 0 0 0 0 0 0 0 0 2 9 0 0 0 0 0 0 0 0 1 1 2 0 1 1 0 0 0 0 0 0 0 0 1 3 1 0 0 0 0 0 0 0 0 1 1 2 2 1 1 0 0 0 0 0 0 0 0 2 3 0 0 0 0 0 0 0 0 1 1 2 4 0 0 0 0 0 0 0 1 0 1 0 0 1 1 5 5 5 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 1 1 0 0 3 3 7 0 0 0 0 0 0 0 0 1 0 0 0 1 2 8 0 0 1 0 0 0 0 0 1 1 0 0 0 0 1 4 9 0 0 1 0 0 0 0 0 0 0 1 0 1 3 0 0 0 0 0 0 1 0 0 0 0 0 1 1 4 1 0 0 0 0 0 0 0 0 1 1 4 2 2 1 0 0 0 0 1 0 0 0 1 0 0 0 1 1 0 0 0 1 0 1 1 0 6 11 4 0 0 0 0 1 1 1 0 1 1 0 0 16 E 1 2 3 4 5 6 7 8 9 0 1 2 3 4 Remaining edges after CS 0 (removal of PURE 0 edge endpoint pair ANDs). 1 8 3 0 1 1 1 0 0 0 0 0 0 0 0 1 9 1 0 0 0 0 0 0 0 0 3 24 on G 7 ( List Version): 1 1 1 111314182022 2 1 3 1 1 1 0 0 0 0 1 1 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 3 4 1 0 0 0 0 0 0 0 0 2 4 4 1 0 0 0 0 0 0 0 0 2 8 3 1 0 1 1 0 0 0 0 0 0 0 0 2 2 14182022 3 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 3 4 4 1 1 0 0 0 0 0 0 0 0 0 0 3 8 3 1 1 0 0 0 0 0 0 0 0 3 9 2 1 0 0 0 0 0 0 0 0 1 3 3 1433 3 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 4 8 3 1 1 1 0 0 0 0 0 0 0 0 4 4 1314 1 3 1 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 5 7 1 1 0 0 0 0 0 0 0 0 5 11 1 0 0 0 0 0 0 0 0 6 7 2 1 0 0 0 0 0 0 0 0 6 6 1117 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 7 17 1 0 0 0 0 0 0 0 0 9 9 9 313334 2 2 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 1 2 3 18, 20, 22 CLQ 4 since 3: 18, 20, 22 E 3 28 1 1 1 5 5 6 7 11 7 3 3 3 4 4 9 8 14 33 24 24 25 30 30 26 33 34 32 2424 28303334 1 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 1 0 0 0 0 0 1 0 0 2525 2632 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 26 32 1 0 0 0 0 0 0 1 0 0 0 0 2727 3034 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 2 2 2 3 3 3 4 8 14 9 9 31 31 33 34 29 32 34 28 34 1 0 0 0 0 0 0 1 0 0 0 0 0 2929 3234 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 17 7 11 8 22 18 12 1 1 1 3 3 3 2 4 Note checkback. Is it required? (No: if 132 in 4 CLQ it’d show up already). Already in CLQ 4 1 1 2 2 UCLQ done. 4 3 3 2 2 3 3 4 4 4 p. Tree version faster? 8 14 1 1 3 3 4 8 9 14 1 6 11 6 7 17 27 30 34 6 1 25 UCLQ 3 Unique 3 cliques as lists 1 4 14 2 32 26 1 1 1 1 2 2 2 2 3 4 8 14 18 20 22 5 29 1 1 1 2 2 2 3 4 3 3 3 4 8 14 since 34 E 3 1 1 4 4 8 13 2 2 4 4 8 14 24 28 34 4 33 19 1 0 1 1 1 1 0 0 0 1 0 1 0 0 0 0 0 16 14 9 21 13 20 31 30 G 7 UCLQ 5 1 2 3 4 8 3030 3334 1 2 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 3131 3334 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 2 2 3 18 20 22 9 MUCLQs 1 2 3 4 14 1 2 3 4 8 32 34 1 0 0 0 0 0 0 0 1 0 0 1 2 3 4 14 6 9 9 7 31 31 17 33 34 1 4 13 11 11 55 66 7 11 24 24 24 28 30 30 34 33 34 25 26 32 27 30 34 Is there a p. Tree Version of this Algorithm ? Is it faster? 3 9 33 29 32 34

n-clique (n-clan, n-club) Community Search on G 6 1 2 G 6 4 5 n-clique (n-clan, n-club) Community Search on G 6 1 2 G 6 4 5 7 n-clique = subgraph s. t. pairs a geodesic path of length n (all pairs are n-connected). 3 c 9 b Downward Closures: Sub. Graph, SGDC (Every subgraph of an n-clique is an n-clique. ) 8 a Path Length, PLDC (If C is an n-clique then C is an (n-1)-clique. ) Apriori, ADC (If C, D are n-cliques of size=k sharing k-1 vertices, then C D is (n+1)-clique) n-clan = n-clique with diameter n. n-club = subgraph of diameter =n. 1 -clique=clique We already have many clique search algorithms, but the pattern we are going to use for n=2… may give us another one? : 1 is 1 conn to 234. 123 1 clique? (23 edge? ). Yes! 124 1 clique? (24 edge? ) Yes! 134 1 clique? (34 edge? ) No! 1234 not a clique by SGDC. 2 is 1 conn to 34. 234 1 clique? No! 3 is 1 conn to just c. 4 is 1 conn to just 7. 5 is 1 conn to 67. 567 1 clique? (67 edge? ) Yes! 6 is 1 conn to 78. 578 1 clique? (78 edge? ) No! 8 is 1 conn to 9 a. 89 a 1 clique? (9 a edge? ) Yes! 9 is 1 conn to abc. 9 ab 1 clique? Yes! 9 ac 1 clique? Yes! 9 bc 1 clique? Yes! So 9 abc is 1 clique by ASGDC and abc is 1 clique by SGDC. 1 is 2 conn to 7 c. 17 c 2 clique? 7 c turned on in SP 1 or SP 2? No! 2 is 2 conn to 7 c. 27 c 2 clique? 7 c turned on in SP 1 or SP 2? No! 3 2 con to 49 abc. 349 2 clique? 49 on in SP 1|2? N! 34 a? 4 a on SP 1|2? N! 34 b? 4 b on SP 1|2? N! 34 c? 4 c on SP 1|2? N! 39 a 2 clique? Y! (9 a on in SP 1). 39 b 2 clique? Y! (9 b on SP 1). 39 c 2 clique? Y! (9 c on SP 1). 3 ab 2 clique? Y! (ab on in SP 1). 3 ac 2 clique? Y! (ac on in SP 1). 3 bc 2 clique? Y! (bc on in SP 1). 39 ab, 39 ac, 3 abc, are 2 cliques by ASGDC. Research questions: 4 2 con to 56. 456 2 clique? Y! (56 on in SP 1). 1. Did I miss anything by using the lower triangular matricies? 5 2 con to 8 only. 2. What about n-clans and n-clubs? 6 2 con to 9 a. 69 a 2 clique? Y! (9 a on in SP 1). 3. Would it be better to start with SP 4, then SP 3, then SP 2, then SP 1 by virtue of 7 2 con to 8 only. PLDC or some other closure or property? 8 2 con to bc. 8 bc 2 clique? Y! (bc on in SP 1). 4. Keeping in mind that it is a big task to creat SPk’s for large graphs, is there a 9 a b are not 2 con to anybody new. better way? Upward Closures: Apriori, ADC (If C, D are n-cliques of size=k sharing k-1 vertices, then C D is (n+1)-clique) All Sub. Graphs, ASGDC (C a subgraph size=k and all subgraphs of C of size (k-1) are n-cliques then C is a n-clique? ? n-clan = n-clique with diameter n. n-club = subgraph of diameter =n. 1 is 4 conn to 8 so 18 is a 4 -clique. 2 is 4 conn to 8 so 28 is a 4 -clique. 3 is 4 conn to 56, 5 is 1 conn to 6 so 356 is a 4 -clique. 4 is 4 conn to 9 ab, 9 a 9 b ab are edges so 49 ab is a 4 -clique. 5 is 4 conn to bc, bc is an edge so 5 bc is a 4 -clique. 7 is 4 conn to bc bc, bc is an edge so 7 bc is a 4 -clique. 1 is 3 conn to 569 ab checking it out, 169 ab is a 3 -clique. SP 1 1 1 3 1 4 0 5 0 6 0 7 0 8 0 9 0 a 0 b 0 c 6 2 SP 2 1 2 3 4 5 6 7 8 9 a b c SP 3 1 2 3 4 5 6 7 8 9 a b c SP 4 1 2 3 4 5 6 7 8 9 a b c SP 1 2 3 4 5 6 7 8 9 a b c 2 3 4 5 6 7 8 9 a b 1 1 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 1 1 1 0 1 1 2 3 4 5 6 7 8 9 a b 0 0 0 1 0 0 0 0 0 1 0 1 0 1 0 0 0 0 1 0 0 0 0 0 0 1 1 2 3 4 5 6 7 8 9 a b 0 0 1 0 1 0 0 1 0 1 0 1 0 0 2 0 0 1 1 0 0 0 3 3 0 0 0 0 1 4 4 0 0 1 0 0 5 5 0 0 0 1 6 0 0 1 0 0 7 7 0 0 0 1 0 0 0 0 1 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 2 3 4 5 6 7 8 9 a b 3 7 1 1 1 3 0 2 2 0 4 0 3 0 3 0 2 2 0 1 1 3 0 2 0 4 0 0 3 0 3 0 2 0 2 0 0 4 3 0 3 3 0 0 3 2 0 2 1 1 1 0 2 2 2 0 2 1 1 0 3 3 0 4 0 4 0 3 3 1 1 2 0 3 3 0 4 0 4 1 1 2 0 0 3 2 0 3 0 4 0 0 0 8 9 a b 1 1 1 0 1 1 2 0 1 1 1 2

G 6 has 4 max cliques: 123 124 567 9 abc. 8 is G 6 has 4 max cliques: 123 124 567 9 abc. 8 is the only point not in an MCLQ and 8 is maximally connected to 9 abc. So the G 6 Clique Aura Partition of: 123 124 567 89 abc G 6 1 5 4 2 3 6 7 c 9 b 8 a E 1 2 3 4 5 6 7 8 9 a b c d e f g h I j k l m n o p q r s t u v w x y 1 c 0 1 1 1 1 0 0 0 1 0 1 0 0 0 0 0 1 0 0 g 1 c 0 1 1 1 1 0 0 0 1 0 1 0 0 0 0 0 1 0 0 b 2 1 0 1 1 0 0 0 0 0 1 0 0 0 9 2 1 0 1 1 0 0 0 0 0 1 0 0 0 7 3 1 1 0 0 0 1 1 1 0 0 0 0 1 1 0 0 0 1 0 a 3 1 1 0 0 0 1 1 1 0 0 0 0 1 1 0 0 0 1 0 9 4 1 1 1 0 0 0 0 0 0 0 6 4 1 1 1 0 0 0 0 0 0 0 5 E 1 2 3 4 5 6 7 8 9 a b c 5 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 3 6 1 0 0 0 0 0 0 0 0 0 0 4 6 1 0 0 0 0 0 0 0 0 0 0 3 7 1 0 0 0 1 1 0 0 0 0 0 0 0 4 7 1 0 0 0 1 1 0 0 0 0 0 0 0 3 8 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 4 9 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 1 5 a 0 0 1 0 0 0 0 0 0 0 0 1 2 b 1 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 3 d 1 0 0 0 0 0 0 0 0 2 e 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 5 f 0 0 0 0 0 0 0 0 1 1 2 g 0 0 0 0 0 0 0 0 1 1 2 h 0 0 0 1 1 0 0 0 0 0 0 0 2 i 1 1 0 0 0 0 0 0 0 0 2 j 0 0 0 0 0 0 0 0 1 1 2 k 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 3 l 0 0 0 0 0 0 0 0 1 1 2 m 1 1 0 0 0 0 0 0 0 0 2 n 0 0 0 0 0 0 0 0 1 1 2 o 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 0 1 0 0 1 1 5 p 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 0 0 3 q 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 1 0 0 3 r 0 0 0 0 0 0 0 0 1 0 0 0 1 2 s 0 0 1 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 1 4 1 0 1 1 1 0 0 0 0 3 t 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 3 2 1 0 1 1 0 0 0 0 3 u 0 0 0 0 0 0 1 0 0 0 1 1 4 u 0 0 0 0 0 0 1 0 0 0 1 1 3 3 1 1 0 0 0 0 0 1 3 v 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 4 4 1 1 0 0 0 0 0 3 5 0 0 0 1 1 0 0 0 2 6 0 0 1 0 1 1 0 0 3 w 1 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 1 1 6 x 0 0 1 0 0 0 0 0 1 1 0 0 1 0 1 1 0 0 0 1 1 1 0 0 b x 0 0 1 0 0 0 0 0 1 1 0 0 1 0 1 1 0 0 0 1 1 1 0 0 6 y 0 0 0 0 1 1 1 0 1 1 0 0 1 1 1 0 0 g y 0 0 0 0 1 1 1 0 1 1 0 0 1 1 1 0 0 9 7 0 0 0 1 1 1 0 0 0 3 8 0 0 0 1 1 0 0 3 9 0 0 0 0 1 1 1 4 E 1 2 3 4 5 6 7 8 9 a b c d e f g h I j k l m n o p q r s t u v w x y a 0 0 0 0 1 1 4 1 c 0 1 1 1 1 0 0 0 1 0 1 0 0 0 0 0 1 0 0 7 1 c 0 1 1 1 1 0 0 0 1 0 1 0 0 0 0 0 1 0 0 6 b 0 0 0 0 1 1 0 1 3 c 0 0 1 0 0 0 1 1 1 0 4 2 1 0 1 1 0 0 0 0 0 1 0 0 0 6 3 1 1 0 0 0 1 1 1 0 0 0 0 1 1 0 0 0 1 0 8 4 1 1 1 0 0 0 0 0 0 0 5 8 1 1 0 0 0 0 0 0 0 0 4 9 1 0 0 0 0 0 0 0 1 0 1 1 5 e 1 1 0 0 0 0 0 0 0 0 1 5 2 1 0 1 1 0 0 0 0 0 1 0 0 0 6 3 1 1 0 0 0 1 1 1 0 0 0 0 1 1 0 0 0 1 0 7 4 1 1 1 0 0 0 0 0 0 0 5 8 1 1 0 0 0 0 0 0 0 0 4 9 1 0 0 0 0 0 0 0 1 0 1 1 5 e 1 1 0 0 0 0 0 0 0 0 1 5 o 0 0 0 0 0 0 0 1 0 1 0 0 1 1 3 s 0 0 1 0 0 0 0 0 1 1 0 0 0 0 1 3 v 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 4 w 1 0 0 0 0 0 0 1 1 0 0 0 1 1 3 x 0 0 1 0 0 0 0 0 1 1 0 0 1 0 1 1 0 0 0 1 1 1 0 0 5 y 0 0 0 0 1 1 1 0 1 1 0 0 1 1 1 0 0 6 x 0 0 1 0 0 0 0 0 1 1 0 0 1 0 1 1 0 0 0 1 1 1 0 0 3 y 0 0 0 0 1 1 1 0 1 1 0 0 1111 1 112345678901234567 1 1123456789 abcdefgh 1 1 0112222233333 089012345678901234 3 ijklmnopqrstuvwxy

E 1 2 4 2 6 7 3 Thm: If h H, dd. H-h E 1 2 4 2 6 7 3 Thm: If h H, dd. H-h = dd. H – (2 idh - edh). So want to remove h s. t. (2 idh – edh) is min. 4 3 c H=G= {123456789 abc} dd. H=38 5 id= 333323334434 dd. H/|VH|=38/12=3. 16 9 b Very Simple Weighted SP 1 and SP 2 K-plex Search 6 ed= 000000 Remove 5 7 8 a Weighting: 0, 1 path nbrs of x times 3; 2 path nbrs of x times 2; Until 8 H= {12346789 abc} dd. H=34 all degrees are weighted, then back to actual subgraph degrees 9 id= 33333334434 dd. H/|VH|=34/11=3. 09 ed= 00001100000 UNWEIGHTED Degrees a b 2 id-ed=66665568868 Remove 6, 7 H={123456789 abc c K-Degree-Difference Community Search: H SG s. t. dd. H Int. Deg. H-Ext. Deg. H k. 1 G 6 5 H= {123489 abc} dd. H=26 id= 333224434 dd. H/|VH|=26/9=2. 88 ed= 000110000 2 id-ed=666338868 Remove 4, 8 deg 333323334434 H= {1239 abc} dd. H=16 id= 2233334 dd. H/|VH|=16/7=2. 28 ed= 1101100 2 id-ed=3365568 Remove 1, 2 H={123456789 abc deg 999923634438 x=1 H={1234578 c deg 99992638 H=15 H=7 kplex k 8 x=1 after cutting 234 1 0 1 1 1 0 0 0 0 3 2 1 0 1 1 0 0 0 0 3 3 1 1 0 0 0 0 0 1 3 4 1 1 0 0 0 0 0 3 5 0 0 0 1 1 0 0 0 2 6 0 0 1 0 1 1 0 0 3 7 0 0 0 1 1 1 0 0 0 3 8 0 0 0 1 1 0 0 3 9 0 0 0 0 1 1 1 4 a 0 0 0 0 1 1 4 b 0 0 0 0 1 1 0 1 3 c 0 0 1 0 0 0 1 1 1 0 4 H={12345 H=6 H=5 kplex k 1 deg 99992 x=1, after cut 23468 H= {39 abc} dd. H=10 id= 13334 dd. H/|VH|=10/5= 2 ed= 21100 2 id-ed=05568 Remove 3 H={123456789 abc deg 999923634438 x=2 H={123456789 abc deg 99962333886 c x=3 H={123456789 abc deg 996946334434 x=4 H= {9 abc} dd. H=9 id= 3333 dd. H/|VH|=9/4=2. 25 H={123456789 abc ed= 1101 deg 333669964434 x=5 2 id-ed=5565 CLQ. Start over w 12345678 H= {12345678} dd. H=17 id= 33232331 dd. H/|VH|=17/8=2. 13 H={123456789 abc ed= 00100002 deg 333669998834 x=6 2 id-ed=66563660 Remove 8 H={1234578 c deg 99992638 H=15 H=7 kplex k 8 x=2 after cutting 234 H={123 c H=6 H=4 2 plex deg 99962 x=3, after cut 2368 H={12345 H=6 H=5 kplex k 1 deg 99992 x=2, after cut 23468 H={123456789 abc H=3 0 plex deg 222623338861 x=3 after cut 1 (actual SG degrees) H={123456789 abc H=3 0 plex deg 996946334434 x=4 after cut 2346 H={123456789 abc H=10 H=5 5 plex deg 333669964434 x=5 after cut 34 H={123456789 abc H=3 0 plex deg 333123314434 x=5 after cut 1 from SG degs H={123456789 abc deg 333669998834 x=6 after cut 34 H={123456789 abc H=3 H=2 1 plex deg 33312333223 x=6 after cut 12 SG degs 211 H={123456789 abc H=3 0 plex deg 333122232234 x=7 after cut 1 SG degs H= {1234567} dd. H=17 id= 3323223 dd. H/|VH|=16/7=2. 28 ed= 0010010 2 id-ed=6636436 Remove 3, 6 H={123456789 abc deg 333969934434 x=7 H={123456789 abc deg 333969998834 x=7 after cut 34 H= {12457} dd. H=6 id= 22312 dd. H/|VH|=6/5=1. 2 ed= 11011 2 id-ed=33613 Remove 5 H={123456789 abc deg 33334969 cc 68 x=8 after cut 34 H={123456789 abc 2 plex deg 333342134433 x=8 after cut 12 SG degs H= {1247} dd. H=4 id= 2231 dd. H/|VH|=4/4=1 ed= 1102 2 id-ed=3360 Remove 7 H={123456789 abc deg 33632639 cc 9 c x=9 H={123456789 abc H=10 H=8 H a kplex k 2 deg 33632639 cc 9 c x=9 after Cutting 2, 3, 6 H= {124} dd. H=3 id= 222 dd. H/|VH|=3/3=1 ed= 111 2 id-ed=333 CLQ. Start over w 35678 H={123456789 abc deg 33632639 cc 9 c x=a H={123456789 abc H=10 H=8 H a kplex k 2 deg 33632639 cc 9 c x=a after cut 2, 3, 6 H={35678} id=02321 ed=30012 dd. H=2 2 id-ed=-34630 dd. H/|VH|=2/5=. 4 Remove 3 H={123456789 abc deg 33632336 cc 9 c x=b H={123456789 abc H=6 H a kplex k 0 deg 33632639 cc 9 c x=b after cut 2, 3, 6 H={5678} id=2321 ed=0012 dd. H=5 2 id-ed= 4630 dd. H/|VH|=5/4=1. 2 Remove 8 H= {567} id=222 ed=011 dd. H=4 2 id-ed= 433 dd. H/|VH|=4/3=1. 33 H={123456789 abc deg 66932336 ccpc x=c H={123456789 abc H=6 H a kplex k 0 deg 66932336 cc 9 c x=c after cut 2, 3, 6 By weighting the initial round we have gotten nearly perfect information for this example (G 6). Weightings, 3 and 2, were arbitrarily chosen but worked here. In general, one should devise a formula to determine them. Also we could weight SP 3 and etc. as well? If we have paid the price of constructing SPk k>1, this is a much simpler way to do it, as compared to the Clique Percolation method of Palla.

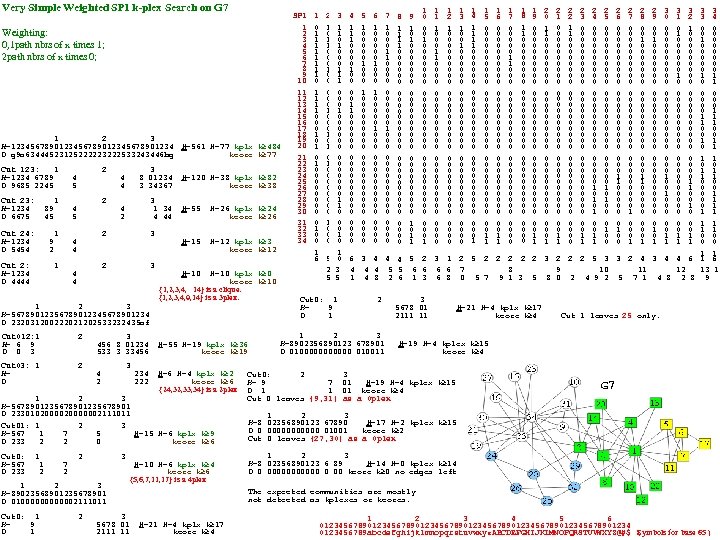Very Simple Weighted SP 1 k-plex Search on G 7 Weighting: 0, 1 path Very Simple Weighted SP 1 k-plex Search on G 7 Weighting: 0, 1 path nbrs of x times 1; 2 path nbrs of x times 0; 1 2 3 H=123456789012345678901234 H=561 H=77 kplx k 484 D g 9 a 63444523125222223222533243446 bg kcore k 77 Cut 123: 1 2 3 H=123456789012345678901234 D 9685322452322522222322243323334367 H=120 H=38 kplx k 82 kcore k 38 Cut 23: 1 2 3 H=123456789012345678901234 D 66753224523225222223323334344 H=55 H=26 kplx k 24 kcore k 26 Cut 24: 1 2 3 H=123456789012345678901234 D 5454322422222322223323334344 H=15 H=12 kplx k 3 kcore k 12 Cut 2: 1 2 3 H=123456789012345678901234 H=10 kplx k 0 D 4444322422222322223323334344 kcore k 10 {1, 2, 3, 4, 14} is a clique. {1, 2, 3, 4, 9, 14} is a 3 plex. 1 2 3 H=56789012345678901234 D 232031200222021202533232435 af Cut 012: 1 2 3 H=56789012345678901234 D 20203120022202120253323233456 Cut 03: 1 2 3 H=56789012345678901234 D 20203120022202120223323233222 H=55 H=19 kplx k 36 kcore k 19 H=6 H=4 kplx k 2 kcore k 6 {24, 32, 33, 34} is a 2 plex 1 2 3 H=5678901235678901 D 23301020000002111011 Cut 01: 1 2 3 H=5678901235678901 H=15 H=6 kplx k 9 D 23301020000000111011 kcore k 6 Cut 0: 1 2 3 H=5678901235678901 H=10 H=6 kplx k 4 D 23301020000000111011 kcore k 6 {5, 6, 7, 11, 17} is a 4 plex 1 2 3 H=89023568901235678901 D 010000002111011 Cut 0: 1 2 3 H=5678901235678901 D 23301020000002111011 H=21 H=4 kplx k 17 kcore k 4 SP 1 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 1 0 1 1 1 1 0 0 0 1 0 1 0 0 0 0 0 1 6 2 1 0 1 1 0 0 0 0 0 1 0 0 0 3 1 1 0 0 0 1 1 1 0 0 0 0 1 1 0 0 0 1 9 0 2 3 5 5 5 1 0 0 0 0 0 0 0 0 6 1 0 0 0 0 0 0 0 0 0 0 7 1 0 0 0 1 1 0 0 0 0 0 0 0 8 1 1 0 0 0 0 0 0 0 0 9 1 0 0 0 0 0 0 0 1 0 1 1 1 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 1 2 1 0 0 0 0 0 0 0 0 0 Cut 0: 1 2 3 H=5678901235678901 D 23301020000002111011 1 2 3 H=89023568901235678901 D 010000002010011 1 3 1 0 0 0 0 0 0 0 0 1 4 1 1 0 0 0 0 0 0 0 0 1 1 5 0 0 0 0 0 0 0 0 1 1 1 6 0 0 0 0 0 0 0 0 1 1 1 7 0 0 0 1 1 0 0 0 0 0 0 0 1 8 1 1 0 0 0 0 0 0 0 0 1 9 0 0 0 0 0 0 0 0 1 1 H=21 H=4 kplx k 17 kcore k 4 2 0 1 1 0 0 0 0 0 0 0 0 1 2 1 0 0 0 0 0 0 0 0 1 1 2 2 1 1 0 0 0 0 0 0 0 0 3 3 3 4 0 0 1 0 0 0 1 1 0 0 0 0 1 1 1 0 0 1 1 0 0 0 1 0 1 1 1 1 0 0 1 1 6 3 4 4 4 5 2 3 1 2 5 2 2 2 3 2 2 2 5 3 3 2 4 3 4 4 6 1 6 4 4 4 5 5 6 6 7 8 9 10 11 12 13 15 1 4 8 2 6 1 3 6 8 0 5 7 9 1 3 5 8 0 2 4 9 2 5 7 1 4 8 2 8 9 5 4 1 1 1 0 0 0 0 0 0 0 2 3 0 0 0 0 0 0 0 0 1 1 2 4 0 0 0 0 0 0 0 1 0 1 0 0 1 1 2 5 0 0 0 0 0 0 0 1 0 0 2 6 0 0 0 0 0 0 1 1 0 0 0 1 0 0 2 7 0 0 0 0 0 0 0 0 1 0 0 0 1 2 8 0 0 1 0 0 0 0 0 1 1 0 0 0 0 1 2 9 0 0 1 0 0 0 0 0 0 0 1 0 1 3 0 0 0 0 0 0 1 0 0 0 0 0 1 1 3 1 0 0 0 0 0 0 0 0 1 1 3 2 1 0 0 0 0 0 0 1 1 0 0 0 1 1 Cut 1 leaves 25 only. H=19 H=4 kplex k 15 kcore k 4 Cut 0: 2 3 H=89023568901235678901 H=19 H=4 kplex k 15 D 010000002010001 kcore k 4 Cut 0 leaves {9, 31} as a 0 plex G 7 1 2 3 H=89023568901235678901 H=17 H=2 kplex k 15 D 010000002010011 kcore k 2 Cut 0 leaves {27, 30} as a 0 plex 1 2 3 H=89023568901235678901 H=14 H=0 kplex k 14 D 01000000201001 kcore k 0 no edges left The expected communities are mostly not detected as kplexes or kcores. 1 2 3 4 5 6 0123456789012345678901234567890123456789 abcdefghijklmnopqrstuvwxyz. ABCDEFGHIJKLMNOPQRSTUVWXYZ@#$ ( Symbols for base 65 )

1 Simple Weighted SP 1, SP 2 K-plex Search on G 8 Weighting 444 1 Simple Weighted SP 1, SP 2 K-plex Search on G 8 Weighting 444 0, 1 path neighbors (12012) times 5 334 2 path nbrs (39893) times 3 221 11 1 1 1 13231 00244105845697461218645954938634545429855587353534965 next cut<18 123456789012345678901234567890123 x=1 41 42 40 39 38 221 11 1 1 1 13231 00244105845697461218645954938634545429855587353534965 instead cut<19 123456789012345678901234567890123 x=1 Cutting C 0 and starting over: Weighting 0, 1 path neighbors (367) times 5 1111445 2 path nbrs (452347483) times 3 11 1 1 1 44544105645697461218645954938634545421675766353534965 G-C 0 degs 123456789012345678901234567890123 x=3 21155 1422 3 1 1 1 1 44522505645887163218645954938634545421675768353534965 next cut<10 123456789012345678901234567890123 x=3 21155 1422 3 1 1 1 1 44522505645887163218645954938634545421675768353534965 next cut<12 123456789012345678901234567890123 x=3 This gives C 2={3, 4, 5, 6, 7, 12, 13, 14, 15, 17, 23, 25, 31, 44, 48, 53} Astronomy is 3, 4, 5, 6, 7, 8, 10, 11, 12, 13, 14, 16, 17, 44, 45, 46, 47, 48, 52, 53 Whereas, so, not a good fit! 11 1 1 1 44444105645697461218645954938634545423675767353534965 123456789012345678901234567890123 With replacement but using as starting vertex, the remaining vertex of highest degree (first, v=12). Weighting 0, 1 SP nbrs times 5 121552 22143135 3231441 2 213 112 231 44202505605655205634025554734894545823675785955594705 cut<20 2 SP nbrs times 3 123456789012345678901234567890123 x=12 121552 22143135 3231441 2 213 112 231 44202505605655205634025554734894545823675785955594705 cut<20 123456789012345678901234567890123 x=12 11111 11 44444 55 Astronomy is 345678 01234 67 45678 23 Weighting 11 1 1 1 44444105645697461218645954938634545423675767353534965 123456789012345678901234567890123 2 SP nbrs times 3 121663 23954136 3231353 2 212 11 14 113 131 44242600640642266634620404734864545223675782958094865 cut<30 Astronomy is 345678 01234 67 45678 23 0, 1 SP nbrs times 6 Weighting 12345678901234567890123456789012 2 SP nbrs times 1 5 astronomy vertices missing (3, 5, 46, 53} and 2 non-astronomy included {21, 24} 0, 1 SP nbrs times 6 54 16 6 14 11 27 20 47 48 24 15 23 21 19 18 46 7 12 10 37 G 8 Thus if we cut next using C 1 -degrees (cut 2, 40) leaves the clique ( 0 plex) C 2={1, 42} 53 52 17 8 45 5 4 3 44 35 221 11 1 1 1 13231 00244105845697461218645954938634545429855587353534965 123456789012345678901234567890123 x=1 Within the Intelligence Class this is the 1 plex, C 1={1, 2, 40, 41, 42} ( only edge missing is (2, 40) ) with C 1 -degrees: 4 3 3 4 4 43 9 36 This gives C 0={1, 2, 9, 39, 40, 41, 42, 43} which is exactly the Intelligence Class except that v=38 (gifted) is missing. It is a kplex k 8 (not that strong of a community!) 2 13 22 49 34 25 5 51 26 28 29 31 32 30 33

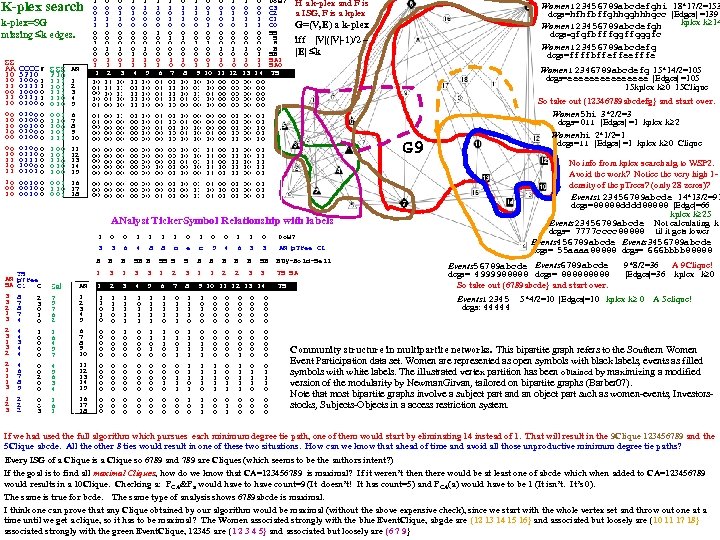10 11 00 11 10 10 0 0 1 01 1 10 0 01 10 11 00 11 10 10 0 0 1 01 1 10 0 01 1 01 0 0 0 111 101 110 010 1 2 3 4 5 1 0 0 0 1 1 10 01 00 10 10 10 00 01 0 0 0 00 1 0 0 0 01 0 001 110 101 111 6 7 8 9 10 01 01 00 00 11 00 00 01 00 00 10 10 00 01 01 01 00 00 01 10 10 10 01 10 00 00 10 10 10 00 01 10 00 00 01 01 01 10 11 00 00 00 01 01 10 00 10 11 01 0 01 1 0 0 01 1 1 0 10 0 01 0 100 101 110 010 100 11 12 13 14 15 00 00 00 00 00 00 00 10 00 01 01 01 10 10 01 00 10 01 10 00 11 11 11 00 00 00 10 01 11 11 11 00 10 10 10 00 01 11 11 11 01 K-plex search k-plex=SG missing k edges. SS AA CCCC F S S S AN 1 0 32 1 0 1 0 0 0 0 1 16 0 0 1 1 0 17 1 0 0 0 0 1 18 0 0 0 1 1 2 11 11 10 01 00 0 0 1 1 0 0 1 3 10 11 11 10 10 1 0 0 0 1 1 1 4 11 01 11 1 1 0 0 0 1 0 1 1 5 10 10 10 1 1 0 0 0 0 0 1 6 01 01 00 1 1 0 0 0 1 0 7 01 11 10 0 1 1 1 0 0 0 1 0 8 10 10 10 01 00 1 1 1 0 0 0 1 9 10 01 11 01 00 0 0 1 1 0 0 0 0 0 1 1 0 10 11 10 00 01 00 10 00 1 1 0 0 1 0 12 00 00 00 1 0 0 1 1 0 0 0 1 0 13 00 00 00 0 0 0 1 1 1 14 00 00 00 Dow? C 3 C 2 C 1 C 0 SS S H B SB SA 1 SA 0 TS H a k-plex and F is a ISG, F is a kplex G=(V, E) a k-plex iff |V|(|V|-1)/2 – |E| k Women 12346789 abcdefg 15*14/2=105 degs=eeeeeeee |Edges| =105 15 kplex k 0 15 Clique G 9 00 00 00 01 10 01 01 00 00 00 01 00 11 10 10 01 00 00 00 01 01 00 11 01 00 01 ANalyst Ticker. Symbol Relationship with labels 1 0 0 1 1 0 3 3 6 4 8 8 a e c 5 4 6 3 3 Dow? AN p. Tree Ct H TS AN p. Tree SA Ct C 3 8 2 3 7 3 2 8 0 1 7 1 3 4 0 2 4 1 3 4 0 1 3 0 3 4 0 2 4 0 1 6 0 1 7 2 1 8 0 3 5 0 1 2 0 2 2 0 3 2 3 B B SS S S H H B B B SB Buy-Hold-Sell 1 3 3 1 2 3 1 1 2 2 3 3 TS SA 7 8 9 10 11 12 13 14 Sal AN 1 2 3 4 5 6 7 5 7 6 2 1 2 3 4 5 1 1 0 1 1 1 0 0 1 1 1 1 1 0 0 1 1 1 1 0 1 0 0 0 0 0 0 0 1 6 4 5 7 6 7 8 9 10 0 0 1 0 0 0 0 0 1 1 1 0 0 0 1 1 1 1 0 0 0 0 0 0 0 1 0 0 0 0 0 4 5 6 3 4 11 12 13 14 15 0 0 0 0 0 0 0 1 0 0 0 1 1 1 1 1 0 0 0 1 1 1 1 0 1 6 1 16 17 18 0 0 0 0 0 0 1 0 0 1 1 1 0 0 0 0 Women 123456789 abcdefghi 18*17/2=153 degs=hfhfbffghhgghhhgcc |Edges| =139 kplex k 14 Women 123456789 abcdefgh degs=gfgfbfffgggfc |14 Women 123456789 abcdefg 1 degs=ffffbffeffeefffe |Edg TS So take out {12346789 abcdefg} and start over. Women 5 hi 3*2/2=3 degs=011 |Edges| =1 kplex k 2 Womenhi 2*1/2=1 degs=11 |Edges| =1 kplex k 0 Clique No info from kplex search alg to WSP 2. Avoid the work? Notice the very high 1 density of the p. Trees? (only 28 zeros)? Events 123456789 abcde 14*13/2=91 degs=88888 dddd 88888 |Edge|=66 kplex k 25 Events 23456789 abcde Not calculating k degs= 7777 cccc 88888 til it gets lower Events 456789 abcde Events 3456789 abcde degs= 55 aaaa 88888 degs= 666 bbbb 88888 Events 6789 abcde 9*8/2=36 A 9 Clique! Events 56789 abcde 1 |Edges|=36 kplex k 0 degs= 499998888825 degs= 88888 So take out {6789 abcde} and start over. Events 12345 5*4/2=10 |Edges|=10 kplex k 0 A 5 clique! degs: 44444 Community structure in multipartite networks. This bipartite graph refers to the Southern Women Event Participation data set. Women are represented as open symbols with black labels, events as filled symbols with white labels. The illustrated vertex partition has been obtained by maximizing a modified version of the modularity by Newman. Girvan, tailored on bipartite graphs (Barber 07). Note that most bipartite graphs involve a subject part and an object part such as women-events, Investorsstocks, Subjects-Objects in a access restriction system. If we had used the full algorithm which pursues each minimum degree tie path, one of them would start by eliminating 14 instead of 1. That will result in the 9 Clique 123456789 and the 5 Clique abcde. All the other 8 ties would result in one of these two situations. How can we know that ahead of time and avoid all those unproductive minimum degree tie paths? Every ISG of a Clique is a Clique so 6789 and 789 are Cliques (which seems to be the authors intent? ) If the goal is to find all maximal Cliques, how do we know that CA=123456789 is maximal? If it weren’t then there would be at least one of abcde which when added to CA=123456789 would results in a 10 Clique. Checking a: PCA&Pa would have to have count=9 (It doesn’t! It has count=5) and PCA(a) would have to be 1 (It isn’t. It’s 0). The same is true for bcde. The same type of analysis shows 6789 abcde is maximal. I think one can prove that any Clique obtained by our algorithm would be maximal (without the above expensive check), since we start with the whole vertex set and throw out one at a time until we get a clique, so it has to be maximal? The Women associated strongly with the blue Event. Clique, abgde are {12 13 14 15 16} and associated but loosely are {10 11 17 18} associated strongly with the green Event. Clique, 12345 are {1 2 3 4 5} and associated but loosely are {6 7 9}

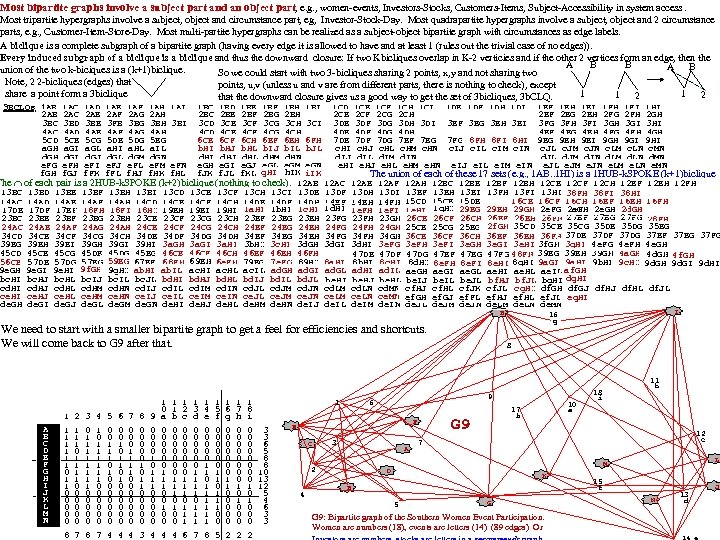Most bipartite graphs involve a subject part and an object part, e. g. , Most bipartite graphs involve a subject part and an object part, e. g. , women-events, Investors-Stocks, Customers-Items, Subject-Accessibility in system access. Most tripartite hypergraphs involve a subject, object and circumstance part, eg, Investor-Stock-Day. Most quadrapartite hypergraphs involve a subject, object and 2 circumstance parts, e. g. , Customer-Item-Store-Day. Most multi-partite hypergraphs can be realized as a subject-object bipartite graph with circumstances as edge labels. A biclique is a complete subgraph of a bipartite graph (having every edge it is allowed to have and at least 1 (rules out the trivial case of no edges)). Every induced subgraph of a biclique is a biclique and thus the downward closure: If two Kbicliques overlap in K-2 verticies and if the other 2 vertices form an edge, then the B B A A B union of the two k-biciques is a (k+1)biclique. So we could start with two 3 -bicliques sharing 2 points, x, y and not sharing two Note, 2 2 -bicliques (edges) that points, u, v (unless u and v are from different parts, there is nothing to check), except share a point form a 3 biclique 1 1 1 2 2 that the downward closure gives us a good way to get the set of 3 bicliques, 3 b. CLQ. 3 BCLQs 1 AB 2 AB 3 BC 4 AC 5 CD a. GH d. GH e. FG f. GH 1 AC 2 AC 3 BD 4 AD 5 CE a. GI d. GI e. FH f. GJ 1 AD 2 AE 3 BE 4 AE 5 CG a. GL d. GJ e. FI f. FK 1 AE 2 AF 3 FB 4 AF 5 DE a. HI d. GL e. FJ f. FL 1 AF 2 AG 3 BG 4 AG 5 DG a. HL d. GM e. FL f. HJ 1 AH 2 AH 3 BH 4 AH 5 EG a. IL d. GN e. FM f. HK 1 AI 1 BC 2 BC 3 CD 4 CD 6 CE b. HI d. HI e. GH f. JK 1 BD 2 BE 3 CE 4 CE 6 CF b. HJ d. HJ e. GI f. JL 1 BE 2 BF 3 CF 4 CF 6 CH b. HL d. HL e. GJ f. KL 1 BF 2 BG 3 CG 4 CG 6 EF b. IJ d. HM e. GL g. HI 1 BH 1 BI 1 CD 1 CE 1 CF 1 CH 1 CI 1 DE 1 DF 1 DH 1 DI 1 EF 1 EH 1 EI 1 FH 1 FI 1 HI 2 BH 2 CE 2 CF 2 CG 2 CH 2 EF 2 EG 2 EH 2 FG 2 FH 2 GH 3 BI 3 CH 3 CI 3 DE 3 DF 3 DG 3 DH 3 DI 3 EF 3 EG 3 EH 3 EI 3 FG 3 FH 3 FI 3 GH 3 GI 3 HI 4 CH 4 DE 4 DF 4 DG 4 DH 4 EF 4 EG 4 EH 4 FG 4 FH 4 GH 6 EH 6 FH 7 DE 7 DF 7 DG 7 EF 7 EG 7 FG 8 FH 8 FI 8 HI 9 EG 9 EH 9 EI 9 GH 9 GI 9 HI b. IL b. JL c. HI c. HJ c. HL c. HM c. HN c. IJ c. IL c. IM c. IN c. JL c. JM c. JN c. LM c. LN c. MN d. HN d. IJ d. IL d. IM d. IN d. JL d. JM d. JN d. LM d. LN d. MN e. FN e. GM e. GN e. HI e. HJ e. HL e. HM e. HN e. IJ e. IL e. IM e. IN e. JL e. JM e. JN e. LM e. LN e. MN h. IK i. IK f. HL The union of each of these 17 sets (e. g. , 1 AB. . 1 HI) is a 1 HUB-k. SPOKE (k+1)biclique The of each pair is a 2 HUB-k. SPOKE (k+2)biclique (nothing to check). 12 AB 12 AC 12 AE 12 AF 12 AH 12 BC 12 BE 12 BF 12 BH 12 CE 12 CF 12 CH 12 EF 12 EH 12 FH 13 BC 13 BD 13 BE 13 BF 13 BH 13 BI 13 CD 13 CE 13 CF 13 CH 13 CI 13 DE 13 DF 13 DH 13 DI 13 EF 13 EH 13 EI 13 FH 13 FI 13 HI 38 FH 38 FI 38 HI 16 CE 16 CF 16 CH 16 EF 16 EH 16 FH 14 AC 14 AD 14 AE 14 AF 14 AH 14 CD 14 CE 14 CF 14 CH 14 DE 14 DF 14 DH 14 EF 14 EH 14 FH 15 CD 15 CE 15 DE 2 e. FH 17 DE 17 DF 17 EF 18 FH 18 FI 18 HI 19 EH 19 EI 19 HI 1 a. HI 1 b. HI 1 c. HI 1 d. HI 1 e. FH 1 e. FI 1 e. HI 1 g. HI 29 EG 29 EH 29 GH 2 e. FG 2 a. GH 2 e. GH 2 d. GH 23 BC 23 BE 23 BF 23 BG 23 BH 23 CE 23 CF 23 CG 23 CH 23 EF 23 EG 23 EH 23 FG 23 FH 23 GH 26 CE 26 CF 26 CH 26 EF 26 EH 26 FH 27 EF 27 EG 27 FG 28 FH 24 AC 24 AE 24 AF 24 AG 24 AH 24 CE 24 CF 24 CG 24 CH 24 EF 24 EG 24 EH 24 FG 24 FH 24 GH 25 CE 25 CG 25 EG 2 f. GH 35 CD 35 CE 35 CG 35 DE 35 DG 35 EG 34 CD 34 CE 34 CF 34 CG 34 CH 34 DE 34 DF 34 DG 34 DH 34 EF 34 EG 34 EH 34 FG 34 FH 34 GH 36 CE 36 CF 36 CH 36 EF 36 EH 36 FH 37 DE 37 DF 37 DG 37 EF 37 EG 37 FG 39 EH 39 EI 39 GH 39 GI 39 HI 3 a. GH 3 a. GI 3 a. HI 3 b. HI 3 c. HI 3 d. GH 3 d. GI 3 d. HI 3 e. FG 3 e. FH 3 e. FI 3 e. GH 3 e. GI 3 e. HI 3 f. GH 3 g. HI 4 e. FG 4 e. FH 4 e. GH 45 CD 45 CE 45 CG 45 DE 45 DG 45 EG 46 CE 46 CF 46 CH 46 EF 46 EH 46 FH 47 DE 47 DF 47 DG 47 EF 47 EG 47 FG 48 FH 39 EG 39 EH 39 GH 4 a. GH 4 d. GH 4 f. GH 56 CE 57 DG 57 EG 59 EG 67 EF 68 FH 69 EH 6 e. FH 79 EG 7 e. FG 89 HI 8 a. HI 8 b. HI 8 c. HI 8 d. HI 8 e. FH 8 e. FI 8 e. HI 8 g. HI 9 a. GI 9 a. HI 9 b. HI 9 c. HI 9 d. GH 9 d. GI 9 d. HI 9 e. GH 9 e. GI 9 e. HI 9 f. GH 9 g. HI ab. IL ac. HI ac. HL ac. IL ad. GH ad. GI ad. GL ad. HI ad. IL ae. GH ae. GI ae. GL ae. HI ae. HL ae. IL af. GH bc. HI bc. HJ bc. HL bc. IJ bc. IL bc. JL bd. HI bd. HJ bd. HL bd. IJ bd. IL bd. JL be. HI be. HJ be. HL be. IJ be. IL be. JL bf. HJ bf. JL bg. HI dg. HI cd. HJ cd. HL cd. HM cd. HN cd. IJ cd. IL cd. IM cd. IN cd. JL cd. JM cd. JN cd. LM cd. LN cd. MN cf. HJ cf. HL cf. JK cf. JL cg. HI df. GH df. GJ df. HL df. JL ce. HI ce. HJ ce. HL ce. HM ce. HN ce. IJ ce. IL ce. IM ce. IN ce. JL ce. JM ce. JN ce. LM ce. LN ce. MN ef. GH ef. GJ ef. FL ef. HJ ef. HL ef. JL eg. HI de. GH de. GI de. GJ de. GL de. GM de. GN de. HI de. HJ de. HL de. HM de. HN de. IJ de. IL de. IM de. IN de. JL de. JM de. JN de. LM de. LN de. MN H We need to start with a smaller bipartite graph to get a feel for efficiencies and shortcuts. We will come back to G 9 after that. 1 1 1 1 1 0 1 2 3 4 5 6 7 8 9 a b c d e f g h i A A B B C C D D E E F F G G H H I I J J K K L L M M N N 1 1 1 0 0 0 1 1 1 1 0 0 0 1 1 1 1 0 0 0 0 0 1 0 1 0 0 0 0 0 1 1 0 0 0 1 0 1 1 0 0 0 0 0 1 1 1 0 0 0 0 0 0 1 1 1 0 0 0 0 1 1 1 0 0 0 1 1 1 1 0 0 0 1 1 1 0 0 0 0 0 0 1 0 0 0 0 3 0 6 0 5 0 8 0 10 0 13 1 12 0 5 1 4 0 6 0 3 8 7 4 4 4 3 4 4 4 6 7 8 5 2 2 2 1 9 3 A 2 4 10 a 17 h G 9 F C 8 6 E I 16 g 11 b 18 i 12 c 7 L M D K B 5 G G 9: Bipartite graph of the Southern Women Event Participation. Women are numbers (18), events are letters (14) (89 edges) Or 15 f J N 13 d

Clique Mining Thm (CLQm) 1 1 0 1 0 0 1 3 D 1 Clique Mining Thm (CLQm) 1 1 0 1 0 0 1 3 D 1 2 3 4 A B C D Use AN ARM-like downward closure alg: b. CCLQk = pairs from b. CLQk-1 that share k-2 vertices. Each such b. CLQk iff the non-shared points E 2 C 3 1 2 2 A B C D E F G 2 1 0 0 1 1 0 0 3 3 0 0 1 1 1 3 4 0 0 1 1 3 G 5 1 1 1 0 0 3 3 1 2 2 3 2 2 G 6 B 4 F 3 5 C 1 0 0 0 1 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 1 1 1 2 1 1 1 F A E 1 CD 1 BD 1 AD Bclq 3 A A B B C C 1 1 2 1 1 1 3 0 1 1 4 1 0 1 5 0 0 1 6 0 0 1 7 0 0 0 1 1 1 1 1 1 0 1 1 D 3 3 6 D D E E F F 4 7 6 1 BC 1 AC C B 6 5 5 5 3 3 2 1 1 AB 2 BC 2 AC 1 AB 1 AC 1 AD 1 AE 1 AF 2 AB 2 AC 2 AE 2 AF 4 AC 4 AD 4 AE 4 AF C 3 A 2 4 D B G 9 B 1 5 2 CE 2 BE 2 AE 4 CD 3 BD 2 BD 3 DE 3 CE 3 BE 2 EF 2 CF 2 BF 2 AF 1 DE 1 CE 3 EF 3 DF 3 CF 3 BF 1 EF 1 DF 1 CF 1 AF 5 DE 5 CE 6 CE 4 AE 5 CD 4 AD 3 BC 4 AC 2 3 4 1 BC 1 BD 1 BE 1 BF 2 BC 2 BE 2 BF 3 BC 3 BD 3 BE 3 BF F E 1 DE 1 CE 1 BE 1 AE 1 EF 1 DF 1 CF 1 BF 1 AF 2 AB 1 6 b. CCLQ 4 14 AC 67 DE 8 FGH b. CCLQ 5 = b. CLQ 3 1 AD 1 AE 1 DE 2 AD 2 AE 2 DE 3 EF 3 EG 3 FG 4 CF 4 CG 4 FG 5 AB 5 AC 5 BC b. CCLQ 4 1 ADE 12 AD 12 AE 12 DE 2 ADE 3 EFG 34 FG 4 CFG 5 ABC = CLQ 4 b. CCLQ 5 12 ADE 34 EFG 34 CFG 2 1 5 6 7 1 CD 1 CE 2 CE 3 CD 3 CE 4 CD 4 CE 5 CD 5 CE 1 CF 2 CF 3 CF 4 CF 1 DE 1 DF 3 DE 3 DF 4 DE 4 DF 5 DE 6 CF 7 Bclq 3 12 A 14 A 12 B 13 B 12 C 13 C 14 C 15 C 16 C 13 D 14 D 15 D 12 E 13 E 14 E 15 E 16 E 17 E 12 F 13 F 14 F 16 F 17 F 8 H b. CLQ 3 1 AC 4 AC 5 BC 6 DE 7 DE 8 FG 8 FH 8 GH 2 1 1 2 2 3 E D 7 3 2 E F G H A 12 A 14 A 24 C 12 D 34 b. CCLQ 4 12 AC 14 AC 12 AC 24 AC 34 BD 24 AD 34 AD 124 A 12 AC b. CLQ 4 12 AC 124 A b. CCLQ 5 12 A 4 C 1 1 0 0 3 5 A B C D E G 2 6 C 1 2 3 4 5 6 7 8 2 2 b. CLQ 3 1 AC 2 AC 3 BD 4 AD B 3 D F Each such b. CLQk iff the non-shared points are in the same part (do not qualify to be an edge). 4 G 5. 1 b 1 (THROW OUT IF NON-SHARED PAIR COULD FORM AN EDGE BUT DOESN’T) G 5 b A 4 24 A 23 B 23 C 24 C 25 C 26 C 34 C 35 C 36 C 45 C 46 C 56 C 34 D 35 D 45 D 23 E 24 E 25 E 26 E 27 E 34 E 35 E 36 E 37 E 45 E 46 E 47 E 56 E 57 E 67 E 23 F 24 F 36 F 37 F 34 F 36 F 37 F 46 F 47 F 67 F 1 EF 2 EF 3 EF 4 EF 6 EF 7 EF = b. CLQ 4 6 EF 6 CF 7 EF F E D C B A

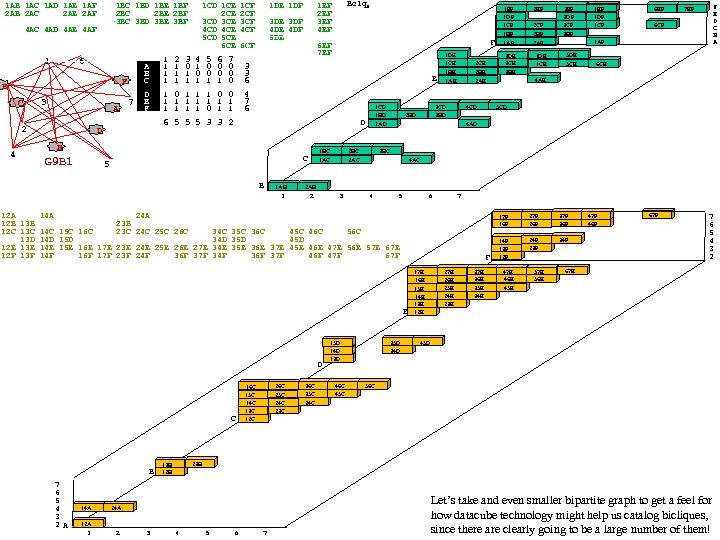1 AB 1 AC 1 AD 1 AE 1 AF 2 AB 2 AC 1 AB 1 AC 1 AD 1 AE 1 AF 2 AB 2 AC 2 AE 2 AF 1 BC 1 BD 1 BE 1 BF 2 BC 2 BE 2 BF 3 BC 3 BD 3 BE 3 BF 4 AC 4 AD 4 AE 4 AF 1 6 F E C 3 A 2 4 1 1 D D E 7 E F F 3 0 1 1 4 1 0 1 5 0 0 1 6 0 0 1 1 CF 2 CF 3 CF 4 CF 1 DE 1 DF 7 0 0 0 F 6 EF 7 EF 3 3 6 4 7 6 E 6 5 5 5 3 3 2 D 1 BC 1 AC C 5 B 1 AB 1 12 A 14 A 12 B 13 B 12 C 13 C 14 C 15 C 16 C 13 D 14 D 15 D 12 E 13 E 14 E 15 E 16 E 17 E 12 F 13 F 14 F 16 F 17 F 1 CD 1 BD 1 AD D B G 9 B 1 Bclq 3 1 EF 2 EF 3 EF 4 EF 3 DE 3 DF 4 DE 4 DF 5 DE 6 CF 1 0 1 1 1 0 0 1 1 1 0 1 1 A A B B C C 2 1 1 CD 1 CE 2 CE 3 CD 3 CE 4 CD 4 CE 5 CD 5 CE 6 CE 2 BC 2 AC C B 24 A 2 3 6 EF 6 CF 1 AF 5 DE 5 CE 7 EF F E D C B A 6 CE 4 AE 3 BC 4 AC 2 3 4 5 6 7 17 F 16 F F 36 C 35 C 34 C 35 D 34 D 15 D 14 D 13 D 46 C 45 C 17 E 16 E 15 E 14 E 13 E 12 E 27 E 26 E 25 E 24 E 23 E 37 E 36 E 35 E 34 E 27 F 26 F 37 F 36 F 14 F 13 F 12 F 24 F 23 F 34 F 47 E 46 E 45 E 57 E 56 E 47 F 46 F 67 F 7 6 5 4 3 2 67 E 45 D 56 C 23 B 12 B 12 A 1 1 DE 1 CE 1 EF 1 DF 1 CF 4 AD 34 C 35 C 36 C 45 C 46 C 56 C 34 D 35 D 45 D 23 E 24 E 25 E 26 E 27 E 34 E 35 E 36 E 37 E 45 E 46 E 47 E 56 E 57 E 67 E 23 F 24 F 36 F 37 F 34 F 36 F 37 F 46 F 47 F 67 F 26 C 25 C 24 C 23 C 2 CF 2 BF 2 AF 3 EF 3 DF 3 CF 3 BF 5 CD 4 CD 24 A 23 B 23 C 24 C 25 C 26 C 15 C 14 C 13 C 12 C 3 DE 3 CE 3 BE 2 EF 2 AB D 14 A 2 CE 2 BE 2 AE 3 CD 3 BD 2 BD E 7 6 5 4 3 2 A 1 DE 1 CE 1 BE 1 AE 1 EF 1 DF 1 CF 1 BF 1 AF 4 5 6 7 Let’s take and even smaller bipartite graph to get a feel for how datacube technology might help us catalog bicliques, since there are clearly going to be a large number of them!

Remember the Sales Data Cube? Each cell contains a sales measurement, e. g. , Remember the Sales Data Cube? Each cell contains a sales measurement, e. g. , the number of sales (may contain many other measurements of product-date-country instances) We will attempt to apply this technology to the task of finding bicliques later, after reviewing the technology. TV PC 1 Qtr 2 Qtr 3 Qtr 4 Qtr U. S. A VCR Canada Mexico Country Pr o du ct Date

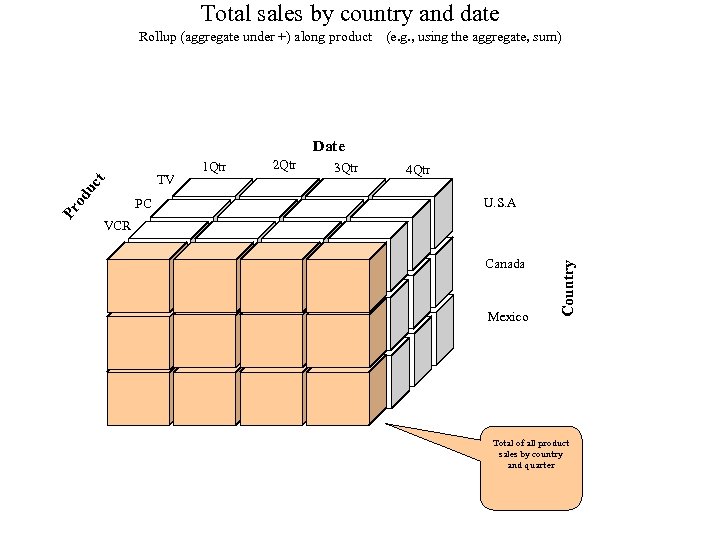Total sales by country and date Rollup (aggregate under +) along product (e. g. Total sales by country and date Rollup (aggregate under +) along product (e. g. , using the aggregate, sum) TV PC 1 Qtr 2 Qtr 3 Qtr 4 Qtr U. S. A VCR Canada Mexico Country Pr o du ct Date Total of all product sales by country and quarter

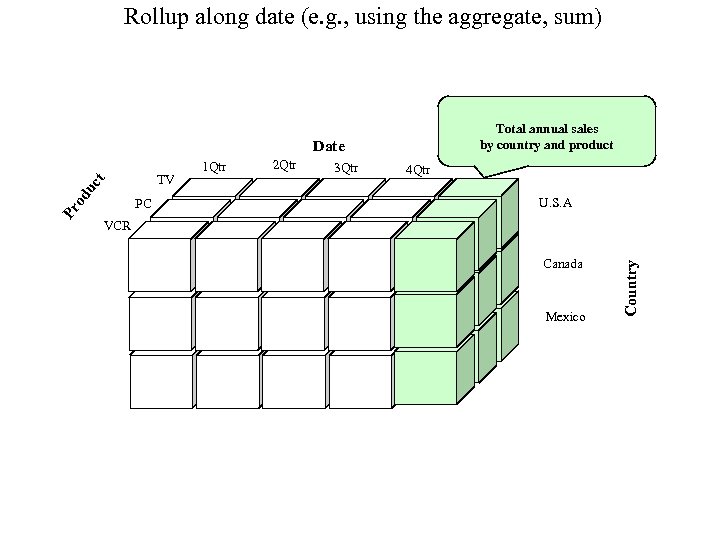Rollup along date (e. g. , using the aggregate, sum) Total annual sales by Rollup along date (e. g. , using the aggregate, sum) Total annual sales by country and product TV PC 1 Qtr 2 Qtr 3 Qtr 4 Qtr U. S. A VCR Canada Mexico Country Pr o du ct Date

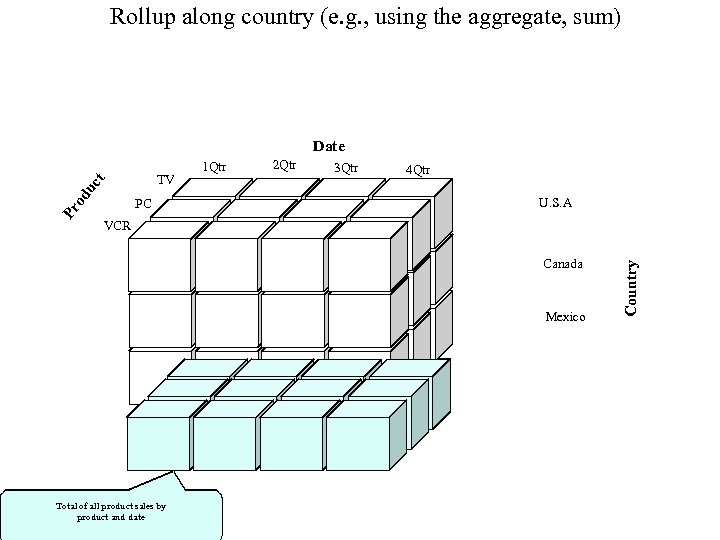Rollup along country (e. g. , using the aggregate, sum) TV PC 1 Qtr Rollup along country (e. g. , using the aggregate, sum) TV PC 1 Qtr 2 Qtr 3 Qtr 4 Qtr U. S. A VCR Canada Mexico Total of all product sales by product and date Country Pr o du ct Date

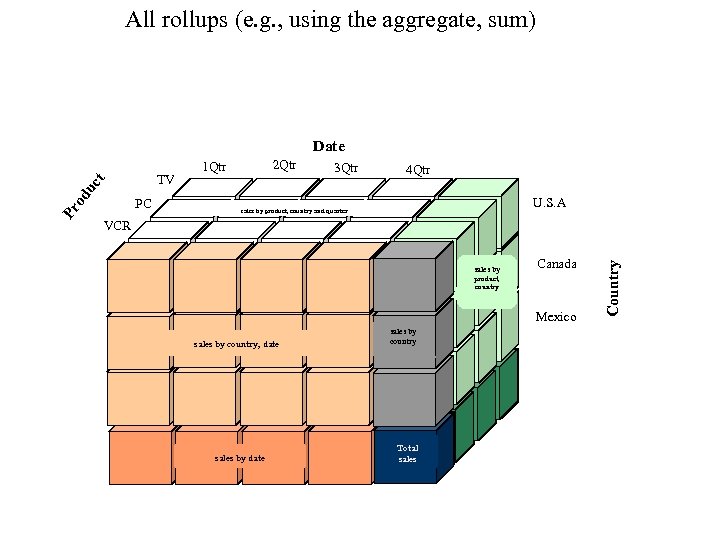All rollups (e. g. , using the aggregate, sum) TV PC 2 Qtr 1 All rollups (e. g. , using the aggregate, sum) TV PC 2 Qtr 1 Qtr 3 Qtr 4 Qtr U. S. A sales by product, country and quarter VCR sales by Canada product, country Mexico sales by country, date sales by country sales by product, country sales by date Total sales Country Pr o du ct Date

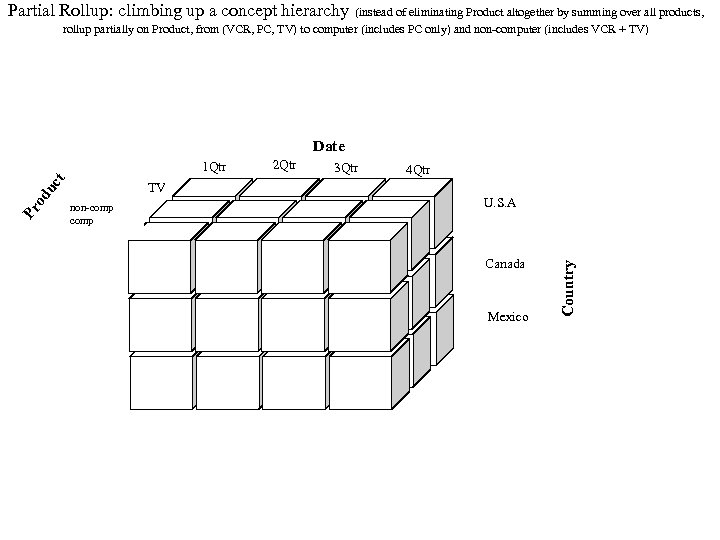Partial Rollup: climbing up a concept hierarchy (instead of eliminating Product altogether by summing Partial Rollup: climbing up a concept hierarchy (instead of eliminating Product altogether by summing over all products, rollup partially on Product, from (VCR, PC, TV) to computer (includes PC only) and non-computer (includes VCR + TV) Date TV non-comp VCR comp 2 Qtr 3 Qtr 4 Qtr U. S. A PC Canada Mexico Country Pr od u ct 1 Qtr

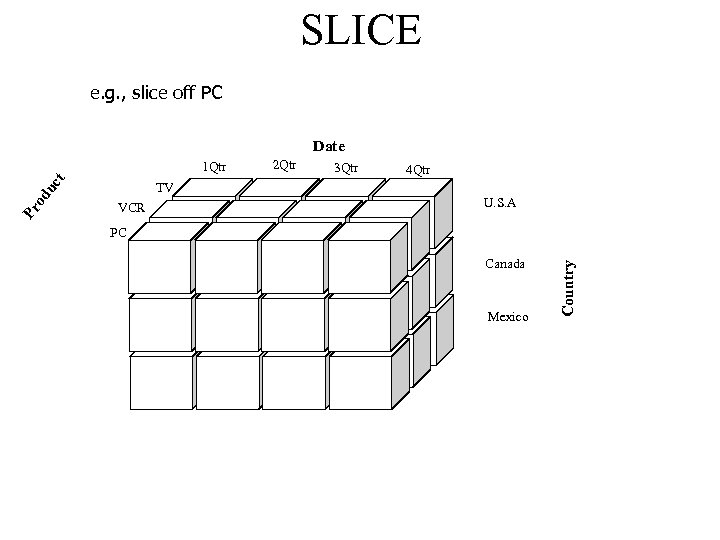SLICE e. g. , slice off PC Date TV VCR 2 Qtr 3 Qtr SLICE e. g. , slice off PC Date TV VCR 2 Qtr 3 Qtr 4 Qtr U. S. A PC Canada Mexico Country Pr od u ct 1 Qtr

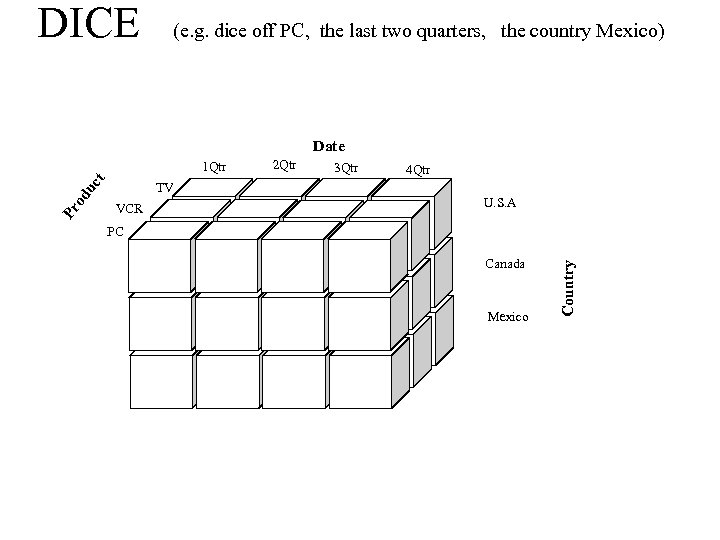DICE (e. g. dice off PC, the last two quarters, the country Mexico) Date DICE (e. g. dice off PC, the last two quarters, the country Mexico) Date 2 Qtr 3 Qtr 4 Qtr TV VCR U. S. A PC Canada Mexico Country Pr o du ct 1 Qtr

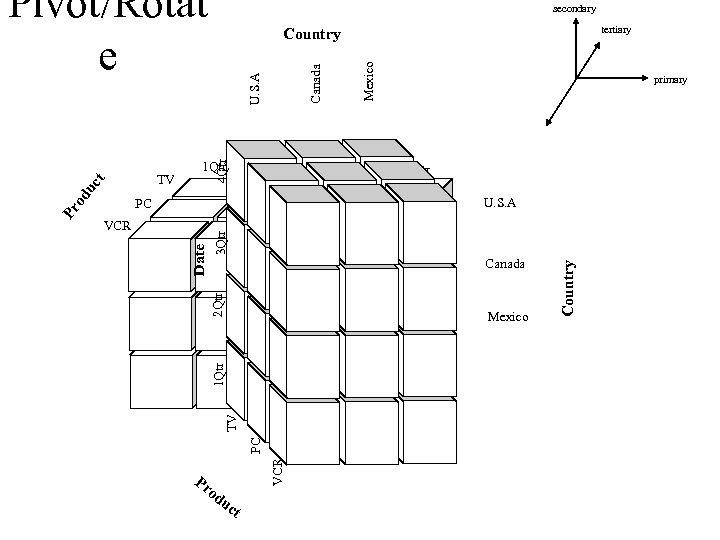Pivot/Rotat e secondary tertiary U. S. A Canada Mexico Country primary 2 Qtr 4 Pivot/Rotat e secondary tertiary U. S. A Canada Mexico Country primary 2 Qtr 4 Qtr 1 Qtr 3 Qtr 4 Qtr U. S. A VCR 3 Qtr PC 2 Qtr Canada VCR PC TV 1 Qtr Mexico Pr od u ct Country TV Date Pr o du ct Date

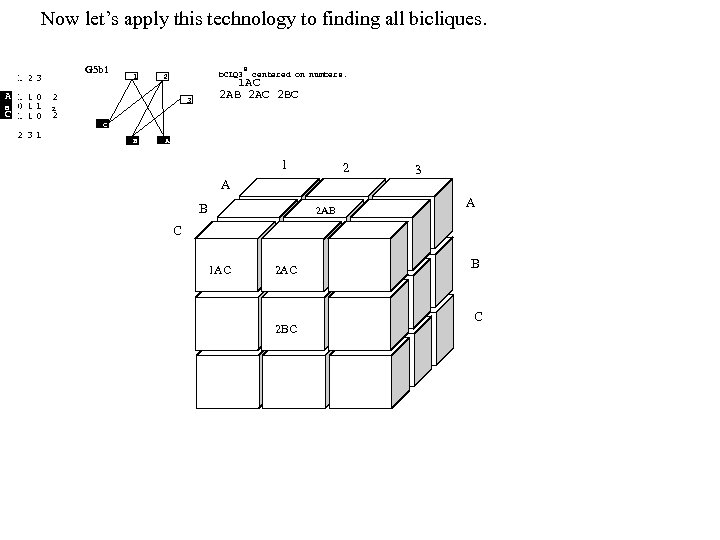Now let’s apply this technology to finding all bicliques. G 5 b 1 123 Now let’s apply this technology to finding all bicliques. G 5 b 1 123 A 110 B 0 1 1 C 110 231 1 s b. CLQ 3 centered on numbers. 2 2 1 AC 2 AB 2 AC 2 BC 3 2 2 C B A 1 2 3 A B 2 AB A C 2 AB 1 AC 2 BC B C

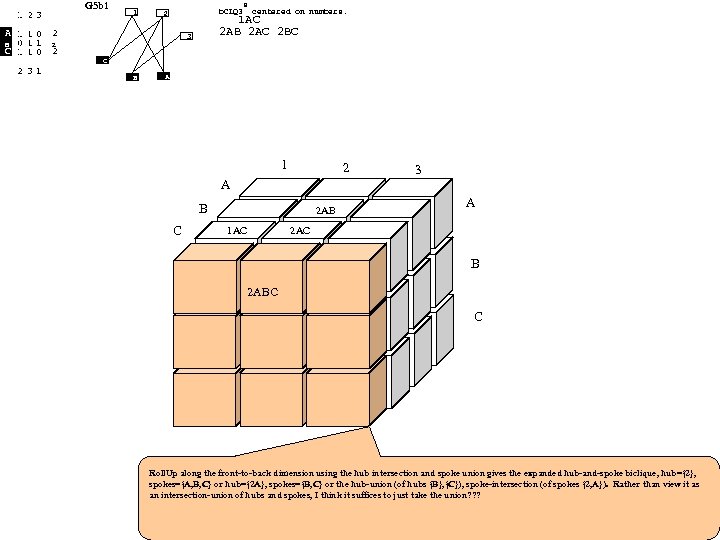G 5 b 1 123 A 110 B 0 1 1 C 110 231 G 5 b 1 123 A 110 B 0 1 1 C 110 231 1 s b. CLQ 3 centered on numbers. 2 2 1 AC 2 AB 2 AC 2 BC 3 2 2 C B A 1 2 3 A B C 2 AB 1 AC A 2 AC B 2 ABC 2 BC C Roll. Up along the front-to-back dimension using the hub intersection and spoke union gives the expanded hub-and-spoke biclique, hub={2}, spokes={A, B, C} or hub={2 A}, spokes={B, C} or the hub-union (of hubs {B}, {C}), spoke-intersection (of spokes {2, A}). Rather than view it as an intersection-union of hubs and spokes, I think it suffices to just take the union? ? ?

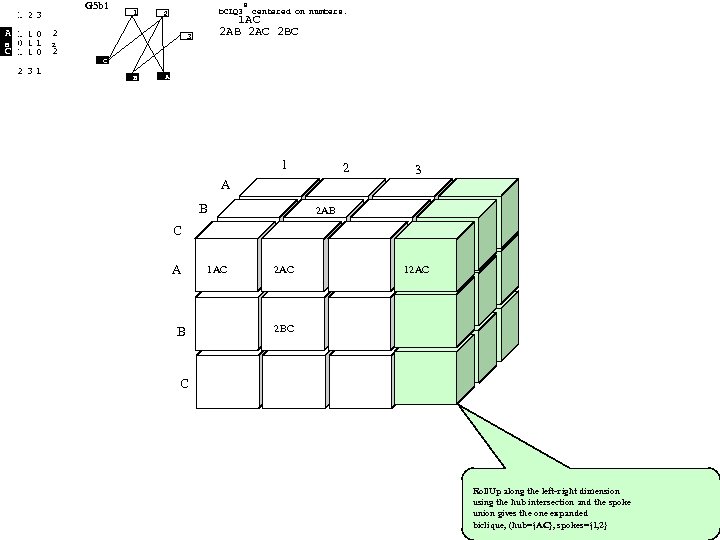G 5 b 1 123 A 110 B 0 1 1 C 110 231 G 5 b 1 123 A 110 B 0 1 1 C 110 231 1 s b. CLQ 3 centered on numbers. 2 2 1 AC 2 AB 2 AC 2 BC 3 2 2 C B A 1 2 3 A B 2 AB C A B 1 AC 2 AC 12 AC 2 BC C Roll. Up along the left-right dimension using the hub intersection and the spoke union gives the one expanded biclique, (hub={AC}, spokes={1, 2}

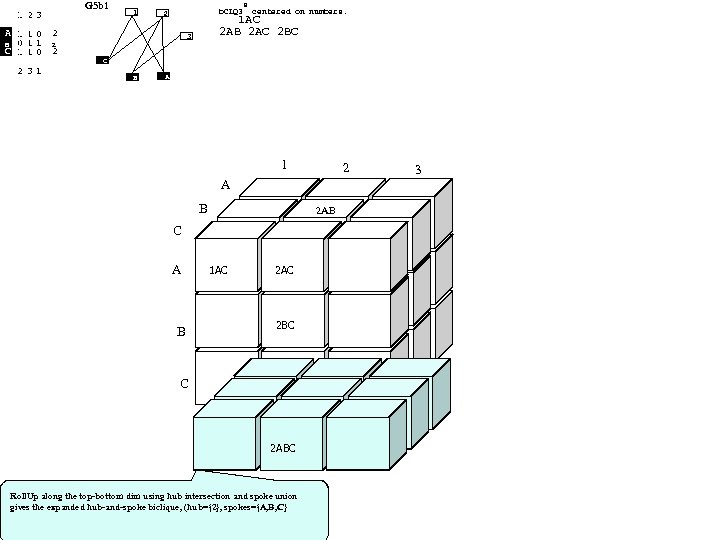G 5 b 1 123 A 110 B 0 1 1 C 110 231 G 5 b 1 123 A 110 B 0 1 1 C 110 231 1 s b. CLQ 3 centered on numbers. 2 2 1 AC 2 AB 2 AC 2 BC 3 2 2 C B A 1 2 A B 2 AB C A B 1 AC 2 BC C 2 ABC Roll. Up along the top-bottom dim using hub intersection and spoke union gives the expanded hub-and-spoke biclique, (hub={2}, spokes={A, B, C} 3

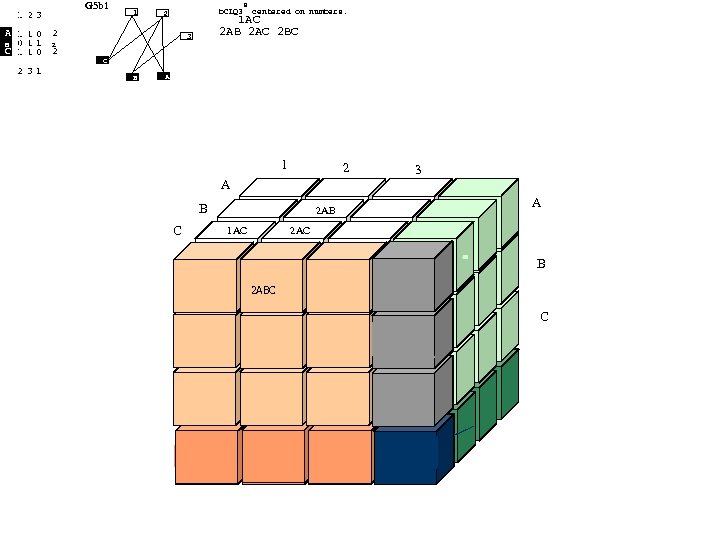G 5 b 1 123 A 110 B 0 1 1 C 110 231 G 5 b 1 123 A 110 B 0 1 1 C 110 231 1 s b. CLQ 3 centered on numbers. 2 2 1 AC 2 AB 2 AC 2 BC 3 2 2 C B A 1 2 3 A B C A 2 AB 1 AC 2 AC 12 AC B 2 ABC C

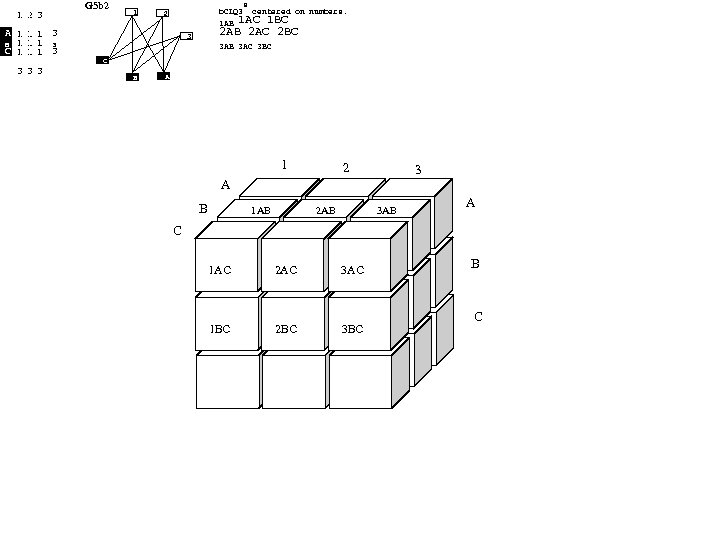1 23 A 1 11 3 B 1 1 1 3 C 1 11 1 23 A 1 11 3 B 1 1 1 3 C 1 11 3 3 33 G 5 b 2 1 s b. CLQ 3 centered on numbers. 2 1 AC 1 BC 2 AB 2 AC 2 BC 1 AB 3 3 AB 3 AC 3 BC C B A 1 2 3 A B 2 AB 1 AB 3 AB A C 2 AB 1 AC 2 AC 3 AC 1 BC 2 BC 3 BC B C

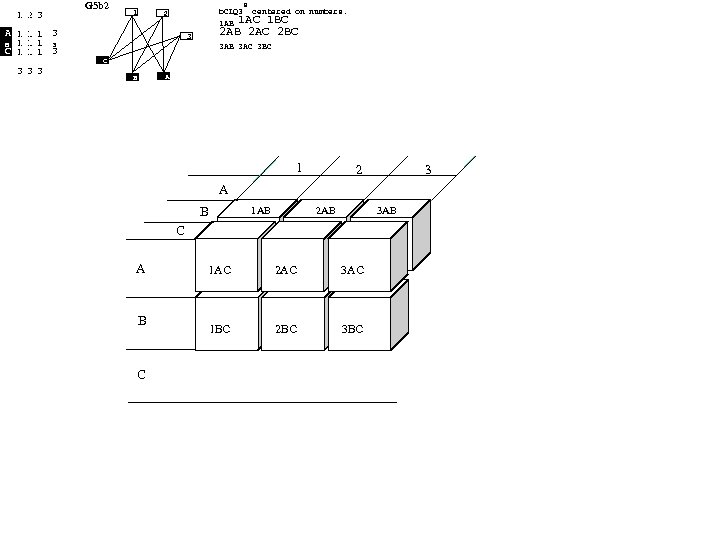1 23 A 1 11 3 B 1 1 1 3 C 1 11 1 23 A 1 11 3 B 1 1 1 3 C 1 11 3 3 33 G 5 b 2 1 s b. CLQ 3 centered on numbers. 2 1 AC 1 BC 2 AB 2 AC 2 BC 1 AB 3 3 AB 3 AC 3 BC C A B 1 2 3 A B 2 AB 1 AB C 2 AB A B C 1 AC 2 AC 3 AC 1 BC 2 BC 3 BC 3 AB

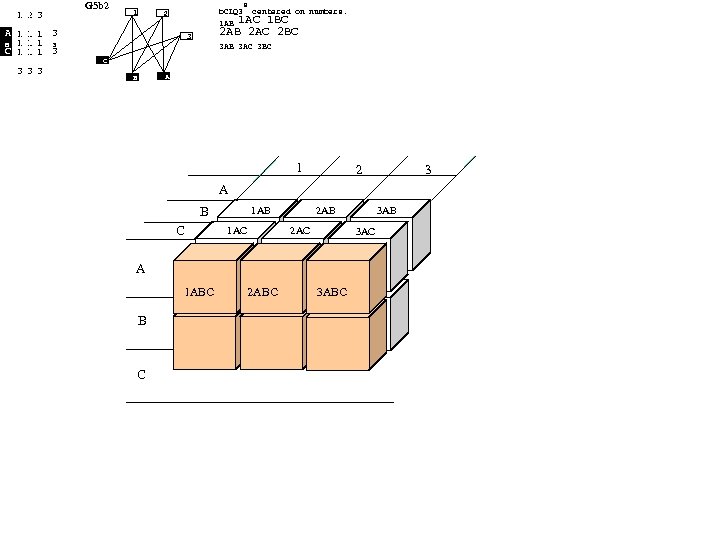1 23 A 1 11 3 B 1 1 1 3 C 1 11 1 23 A 1 11 3 B 1 1 1 3 C 1 11 3 3 33 G 5 b 2 1 s b. CLQ 3 centered on numbers. 2 1 AC 1 BC 2 AB 2 AC 2 BC 1 AB 3 3 AB 3 AC 3 BC C A B 1 2 3 A C A 1 AC 1 ABC B C 2 AB 1 AB B 1 BC 2 AC 3 AB 3 AC 2 AC 2 ABC 2 BC 3 ABC 3 BC

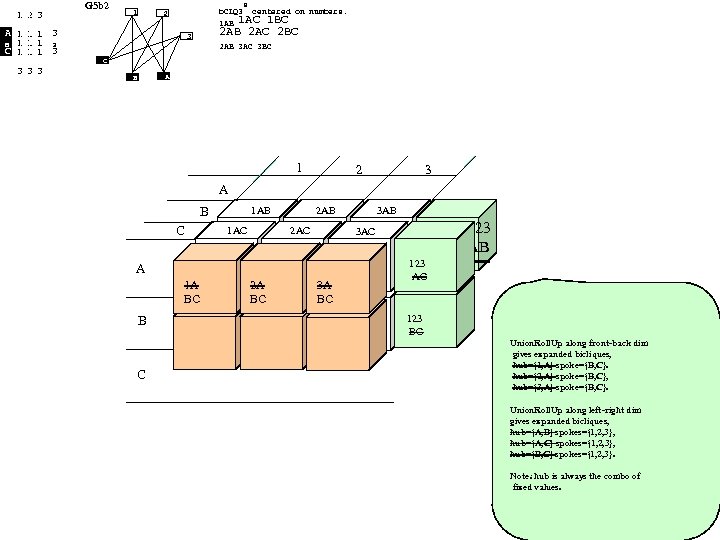1 23 A 1 11 3 B 1 1 1 3 C 1 11 1 23 A 1 11 3 B 1 1 1 3 C 1 11 3 3 33 G 5 b 2 1 s b. CLQ 3 centered on numbers. 2 1 AC 1 BC 2 AB 2 AC 2 BC 1 AB 3 2 AB 3 AC 3 BC C A B 1 2 3 A C A 1 AC C 2 AC 1 AC 1 A BC B 2 AB 1 AB B 123 AC 3 A BC 2 BC 123 AB 3 AC 2 AC 2 A BC 1 BC 3 AB 3 BC 123 BC Union. Roll. Up along front-back dim gives expanded bicliques, hub={1, A} spoke={B, C}. hub={2, A} spoke={B, C}, hub={3, A} spoke={B, C}. Union. Roll. Up along left-right dim gives expanded bicliques, hub={A, B} spokes={1, 2, 3}, hub={A, C} spokes={1, 2, 3}, hub={B, C} spokes={1, 2, 3}. Note: hub is always the combo of fixed values.

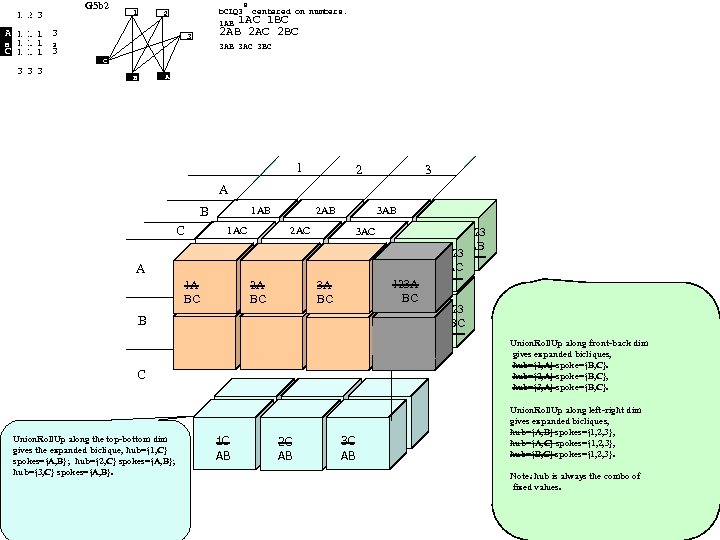1 23 A 1 11 3 B 1 1 1 3 C 1 11 1 23 A 1 11 3 B 1 1 1 3 C 1 11 3 3 33 G 5 b 2 1 s b. CLQ 3 centered on numbers. 2 1 AC 1 BC 2 AB 2 AC 2 BC 1 AB 3 3 AB 3 AC 3 BC C A B 1 2 3 A C A 1 AC 3 AC 2 AC 2 A BC 1 BC 3 AB 2 AC 1 AC 1 A BC B 2 AB 1 AB B 3 A BC 2 BC 3 BC Union. Roll. Up along front-back dim gives expanded bicliques, hub={1, A} spoke={B, C}. hub={2, A} spoke={B, C}, hub={3, A} spoke={B, C}. C Union. Roll. Up along the top-bottom dim gives the expanded biclique, hub={1, C} spokes={A, B}; hub={2, C} spokes={A, B}; hub={3, C} spokes={A, B}. 123 AB 123 AC 123 A BC 123 BC 1 C AB 2 C AB 3 C AB Union. Roll. Up along left-right dim gives expanded bicliques, hub={A, B} spokes={1, 2, 3}, hub={A, C} spokes={1, 2, 3}, hub={B, C} spokes={1, 2, 3}. Note: hub is always the combo of fixed values.

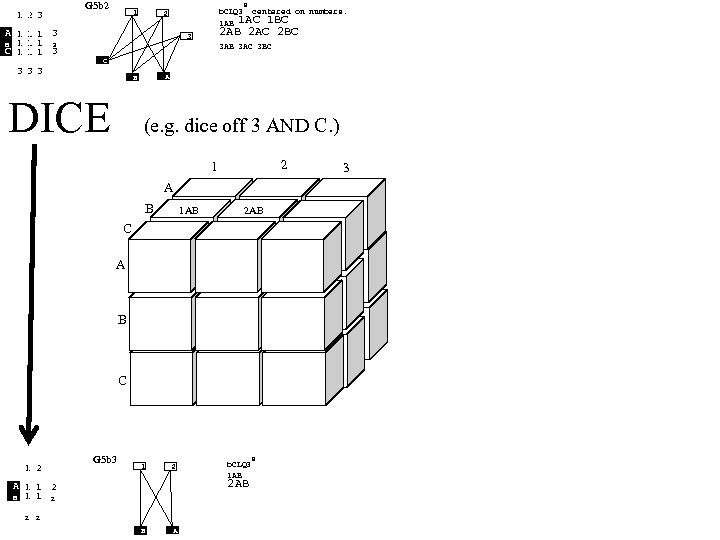1 23 A 1 11 3 B 1 1 1 3 C 1 11 1 23 A 1 11 3 B 1 1 1 3 C 1 11 3 G 5 b 2 1 s b. CLQ 3 centered on numbers. 2 1 AC 1 BC 2 AB 2 AC 2 BC 1 AB 3 3 AB 3 AC 3 BC C 3 33 A B DICE (e. g. dice off 3 AND C. ) 2 1 A B 1 AB 2 AB C A B C 1 2 G 5 b 3 1 2 s b. CLQ 3 1 AB 2 AB A 1 1 2 B 1 1 2 2 2 B A 3

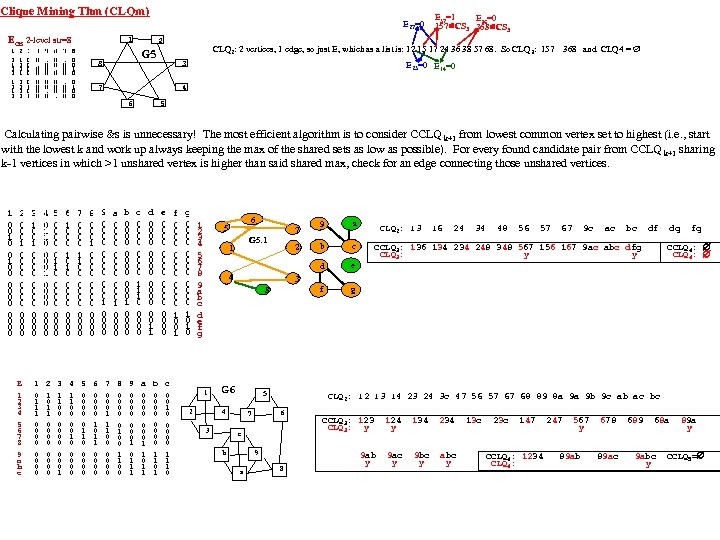Clique Mining Thm (CLQm) E 27=0 EG 5 2 -level str=8 1 0 0 Clique Mining Thm (CLQm) E 27=0 EG 5 2 -level str=8 1 0 0 1 0 2 1 0 0 0 0 3 0 0 0 1 4 0 1 0 0 0 5 1 0 0 0 1 0 6 0 0 1 7 1 0 0 0 1 8 0 0 1 0 0 2 CLQ 2: 2 vertices, 1 edge, so just E, which as a list is: 12 15 17 24 36 38 57 68. So CLQ 3: 157 368 and CLQ 4 = G 5 8 E 57=1 E 36=0 157 CS 3 368 CS 3 E 25=0 E 14=0 3 4 7 5 6 Calculating pairwise &s is unnecessary! The most efficient algorithm is to consider CCLQ k+1 from lowest common vertex set to highest (i. e. , start with the lowest k and work up always keeping the max of the shared sets as low as possible). For every found candidate pair from CCLQ k+1 sharing k-1 vertices in which >1 unshared vertex is higher than said shared max, check for an edge connecting those unshared vertices. 1 0 0 0 0 0 2 0 0 0 1 0 0 0 E 1 2 3 4 5 6 7 8 9 a b c 3 1 0 0 0 0 1 0 1 1 1 0 0 0 0 4 0 1 1 0 0 0 2 1 0 1 1 0 0 0 0 5 0 0 0 1 1 0 0 0 0 0 3 1 1 0 0 0 0 0 1 6 1 0 0 0 0 0 4 1 1 0 0 0 0 0 7 0 0 1 1 0 0 0 0 0 5 0 0 0 1 1 0 0 0 8 0 0 0 1 0 0 0 6 0 0 1 0 1 1 0 0 9 0 0 0 1 0 0 7 0 0 0 1 1 1 0 0 0 a 0 0 0 1 0 0 8 0 0 0 1 1 0 0 b 0 0 0 1 0 0 9 0 0 0 0 1 1 1 c 0 0 0 0 1 1 1 0 0 0 a 0 0 0 0 1 1 d 0 0 0 0 1 1 b 0 0 0 0 1 1 0 1 e 0 0 0 0 c 0 0 1 0 0 0 1 1 1 0 f 0 0 0 1 0 0 1 g 0 0 0 1 0 6 5 G 5. 1 1 2 4 G 6 5 4 2 3 b c e g CLQ 2: 13 16 24 34 48 56 57 67 9 c ac bc df dg fg CCLQ 4: CCLQ 3: 136 134 248 348 567 156 167 9 ac abc dfg CLQ 3: y y 3 8 1 a f 7 9 d 1 2 3 4 5 6 7 8 9 a b c d e f g CLQ 2: 12 13 14 23 24 3 c 47 56 57 67 68 89 8 a 9 a 9 b 9 c ab ac bc 6 7 c 9 b a 8 CCLQ 3: 123 CLQ 3: y 124 y 134 234 9 ab y 9 ac y 9 bc y abc y 13 c 23 c 147 CCLQ 4: 1234 CLQ 4: 247 567 y 89 ab 678 89 ac 689 68 a 9 abc y 89 a y CCLQ 5=

More Complex Graph Structures? The vertex-labelled, edge-labelled graph ANalyst Ticker. Symbol Relationship with labels More Complex Graph Structures? The vertex-labelled, edge-labelled graph ANalyst Ticker. Symbol Relationship with labels 1 We can interpret this structure many ways, 1. as a relationship with entity tables; 2. as a AN[lysist] Table with attributes, the AN attributes (SA, Ct, C, Sal) plus each Ticker. Symbol p. Tree as an additional attribute (the TS attributes (Dow? , Ct, BHS, SA) are not captured in this interpretation); 3. as a T[icker] S[ymbol] or Stock Table with attributes, the TS attributes (Dow? , Ct, 0 0 1 1 0 1 0 0 1 1 0 3 3 6 4 8 8 a e c 5 4 6 3 3 Dow? AN p. Tree Ct H TS AN p. Tree SA Ct C 3 8 2 3 7 3 2 8 0 1 7 1 3 4 0 2 4 1 3 4 0 1 3 0 3 4 0 2 4 0 1 6 0 1 7 2 1 8 0 3 5 0 1 2 0 2 2 0 3 2 3 B B SS S S H H B B B SB Buy-Hold-Sell 1 2 2 3 3 TS SA 1 3 3 1 2 3 1 Sal AN 1 2 3 4 5 6 7 8 9 10 11 12 13 14 7 5 7 6 2 1 2 3 4 5 1 1 0 1 1 1 0 0 1 1 1 1 1 0 0 1 1 1 1 0 1 0 0 0 0 0 0 0 1 6 4 5 7 6 7 8 9 10 0 0 1 0 0 0 0 0 1 1 1 0 0 0 1 1 1 1 0 0 0 0 0 0 0 1 0 0 0 0 0 4 5 6 3 4 11 12 13 14 15 0 0 0 0 0 0 0 1 0 0 0 1 1 1 1 1 0 0 0 1 1 1 1 0 1 6 1 16 17 18 0 0 0 0 0 0 1 0 0 1 1 1 0 0 0 0 1 1 0 0 0 1 1 2 11 11 10 01 00 0 0 1 1 0 0 1 3 10 11 11 10 10 1 0 0 0 1 1 1 4 11 01 11 1 1 0 0 0 1 0 1 1 5 10 10 10 1 1 0 0 0 0 0 1 6 01 01 00 1 1 0 0 0 1 0 7 01 11 10 0 1 1 1 0 0 0 1 0 8 10 10 10 01 00 1 1 1 0 0 0 1 9 10 01 11 01 00 0 0 1 1 0 0 0 0 0 1 1 0 10 11 10 00 01 00 10 00 1 1 0 0 1 0 12 00 00 00 1 0 0 1 1 0 0 0 1 0 13 00 00 00 0 0 0 1 1 1 14 00 00 00 TS BHS, SA) plus each Analyst p. Tree as an additional attribute (the AN attributes (SA, Ct, F, Sal) are not captured in this interpretation); We can include this relationship with other relationships sharing entities by using the Rolo. Dex Model (next slide). The graph could be 3 D, 4 D (i. e. , edges are triples, quadruples), etc. The graph could also be edge labelled. A convenient way to capture edge labels is by making the cell content of each matrix cell into the label structure rather than just a yes/no bit. As a simple but pertinent example, suppose we have a 0 -3 rating of each Analyst-Stock pair which measure how much that Analysts know about that stock. We just change each bit to a decimal number in [0, 3] (or bitslice those using two bits instead of on, so that the matrix columns are 2 -bit p. Tree. Sets rather than just one p. Tree). 10 11 00 11 10 10 0 0 1 01 1 10 0 01 1 01 0 0 0 111 101 110 010 1 2 3 4 5 1 0 0 0 1 1 10 01 00 10 10 10 00 01 0 0 0 00 1 0 0 0 01 0 001 110 101 111 6 7 8 9 10 01 01 00 00 11 00 00 01 00 00 10 10 00 01 01 01 00 00 01 10 10 10 01 10 00 00 10 10 10 00 01 10 00 00 01 01 01 10 11 00 00 00 01 01 10 00 10 11 01 0 01 1 0 0 01 1 1 0 10 0 01 0 100 101 110 010 100 11 12 13 14 15 00 00 00 00 00 00 00 10 00 01 01 01 10 10 01 00 10 01 10 00 11 11 11 00 00 00 10 01 11 11 11 00 10 10 10 00 01 11 11 11 01 In full p. Tree form: SS AA CCCC F S S S AN 1 0 32 1 0 1 0 0 0 0 1 16 0 0 1 1 0 17 1 0 0 0 0 1 18 Dow? C 3 C 2 C 1 C 0 SS S H B SB SA 1 SA 0 TS 00 00 00 01 10 01 01 00 00 00 01 00 11 10 10 01 00 00 00 01 01 00 11 01 00 01 If C measures the “Correctness Level” of the Analyst over recent days or weeks over all stock (e. g. , based on backward analysis of previous sentiment analysis and the actual performance of the stock) and the cell numbers measure the correctness of that Analyst on that Stock, then a signal might be to mask C>=2 and for those Analysts find the average Correctness for each stock, then mask out those Stock for which the number of Analysts is between two thresholds (want a high average but also more than one analyst but not too many).

Every Entity (Gene, Term, Experiment, Person, Document, Item, Stock, Course, Movie) has an Entity. Every Entity (Gene, Term, Experiment, Person, Document, Item, Stock, Course, Movie) has an Entity. Table of many descriptive attributes (columns). They aren’t shown here. For example, on the previous slide we show the descriptive columns of Stocks(Dow? , Count, BHS, SA) and Analysts(SA, Count, Female? , Salary. In. Billions), not shown here. Tweets are Documents, so the Tweet-Tweeter relationship is a Document-Author relationship (Tweetee, hashtag, etc. are Edge Labels). Stock In looking for signals that no one else uses: What if an Investor BUYS an island in the Mediterranean? What if an Investor’s best friend buys lots of stock in an Online University? 1 2 Stock. Investor relationship 3 4 Conf(A B) Supp(A) = Cus. Freq(Item. Set) =Supp(A B)/Supp(A) 5 6 7 16 Item Friends relationship 6 itemset 5 BUYS 4 3 2 People Author Customer Term. Document 1 1 1 PI 3 4 4 5 7 2 2 3 5 6 Item. Set 1 2 3 4 0 0 antecedent 1 1 1 Auth 1 1 1 Doc gene rel (ppi) 3 2 1 1 3 1 docdoc 1 1 1 Gene Enroll 2 1 movie 4 Do c 1 Item. Set 1 4 Course 2 People term G exp. PI 1 1 2 3 4 5 6 3 4 3 0 0 Doc 3 0 0 2 7 0 2 1 0 0 0 Expg ene Ex 1 The Multi-Relationship Model 5 0 3 0 1 0 0 0 4 0 5 6 7 0 5 0 0 0 1 0 4 0 0 0 0 1 0 customer rates movie 0 2 Share. Stem term rel Cell. Label=stem 0 0 t p 3 1 3 5 0 0 0 0 customer rates movie as 5 relationships 0 0 0 1 0 5 6 16

More Complex Graph Structures? Hyper. Graphs, clique. Trees (c. Trees), GRAPH (linear edges, 2 More Complex Graph Structures? Hyper. Graphs, clique. Trees (c. Trees), GRAPH (linear edges, 2 vertices) k. PARTITE Graph or just k. PART Graph (V=! Vi i=1. . k (x, y) E x, y same Vi ) Motifs k. Hyper. Graph (edges=k vertex set) k. PART Hyper. Graph (V=! Vi i=1. . k (x 1. . xk) E xj, xj same Vi ) Bi. Part. Clique Mining finds Max. Cliques (bicliques) at cost of pairwise &s. Each LETp. Tree MCLQ unless pairwise & with same ct. A&B, B w Ct(A&B)=Ct(A) is MCLQ potential for a k-plex [k-core] mining alg here. Instead of Ct(A&B)=Ct(A), consider. E. g. , Ct(A&B)=Ct(A)-1. Each such p. Tree, C, would be missing just 1 vertex (1 edge). Taking any MCLQ as above, ANDing in Cp. Tree would produce a 1 -plex. ANDing in k such C’s would produce a k-plex. In fact, suppose we have produced a k-plex in such a manner, then ANDing in any C with Ct(C)=Ct(A)-h would produce a (K+h)-plex. &i=1. . n. Ai is a [ i=1. . n. Ct(Ai)]-Core Tri. PART Clique Mining Algorithm? In a Tripartite Graph edges must start and end in different vertex parts. E. g. , PART 1=tweeters; PART 2=hashtags; PART 3=tweets. Tweeters-to-hashtags is many-to-many? Tweeters-to-tweets is many-to-many (incl. retweets)? ; hashtags-to-tweets is many-to-many? Multi. PART Graphs Bi. PART, Tri. PART (have 2, 3 PARTs respectively but still an edge is a linear (between two vertices) … No edge can start and end in the same PART. 0 D 1 Hyper. Clique Mining: A 3 hyper. Graph has 3 vertex PARTS and each edge is a planar triangle (defined by a vertex triple, one from each PART). 1 Stock recommender is 3 hyper. Graph (Investors, Stocks, Days). A triangular edge connects Investor k, Stock X, and Day n if k recommends X on day n. A 3 hyper. Clique is I 0 1 a community s. t. all investors in clique recommend all stocks in the clique on each day in clique. Tweet ex: PART 1=tweeters; PART 2=hashtags; PART 3=tweets. 1 1 Conjecture: Kmulti. Cliques and Khyper. Cliques are in 1 -1 correspondence (both are defined by a K PART vertex set)? So, only one mining process needed? 1 S We will represent these common objects with clique. Trees (c. Trees). A c. Tree bitmaps each PART of the clique. E. g. , the c. Tree for Inv={2, 3}; Stock={A, B} Day={ , }: 0 Cts Cliques, Kplexes and Kcores are subgraphs (communities) defined using an internal edge count. A Motif is a subgraph defined using external “isomorphism into the graph” count. A motif must occur (isomorphically) in the graph more times than “expected”. Criticism: Some authors argue[62] that a motif structure does not necessarily determine function. Recent research [64] shows the connections of a motif to the network, is too important to draw function inferences just from local structure. [65] Research shows certain topological features of biological networks naturally give rise to canonical motifs, . [66] Most find induced Motifs. A graph, G′, is a subgraph of G (G′⊆G) if V′⊆V and E′⊆E∩(V′×V′). If G′⊆G and G′ contains all ‹u, v›∈E with u, v∈V′, G′ is induced subgraph. G′ and G are isomorphic (G′↔G), if a bijection f: V′→V with ‹u, v›∈E′⇔‹f(u), f(v)›∈E u, v∈V′. G″⊂G and an isomorphism between G″ and G′, G′ appears in G). The number of appearances G′ in G is the frequency FG of G′ in G, FG(G’). G is recurrent or frequent in G, when FG(G’)>threshold (pattern=frequent subgraph). Motif discovery includes exact counting, sampling, pattern growth. Motif discovery has 2 steps: calculate the # of occurrences; evaluating the significance. Are Stock-Inv or Stock-Inv-Day Motifs useful? Some questions/theorems/thoughts: 1. 2. 3. 4. 5. All K-Paths are isomorphic (thus, there’s alway a Kpath motif). A Shortest. KPath is an Induced subgraph. What does sequence Frequency(1 Path. Motif)=|V|, Frequency(2 Path. Motif), …tell? Sequence of Frequency(Shortest 1 Path), Frequency(Shortest 2 Path), …? Sequence Frequency(Max. Shortest 1 Path), Frequency(Max. Shortest 2 Path)… tell us? where a Max. S 2 P is not part of a S 3 P. Extend to Hyper. Edges? What is a path in, e. g. , a 3 Hyper. Graph? Both? 2 HGInterface 3 Hyper. Graph. Path. 1 HGI 3 HGP. (In general, h. HGIk. HGP, where 0

Introduction to 2 PART Graph Community Search: For a multipartite graph the concept of Introduction to 2 PART Graph Community Search: For a multipartite graph the concept of community is still related to a large density of edges between members of the same group. A clique in a 2 PART (bipartite) graph to be a bipartite subset of vertices with all possible edges. 2 PART Induction thm: In a bipartite graph, a Kclique and 3 clique that share an edge form a (K+1)clique iff all edges that can exist, from the nonshared Kclique vertices to the non-shared 3 clique vertex, do exist. 2 PART 3 Clique thm: a pair of vertices from part 1, a, b and a vertex from the part 2, 1, form a 3 Clique iff both possible edges a 1, b 1 exist. CLQ 3 is constructed by listing each vertex pair in each p. Tree along with the naming vertex of the p. Tree. a a The 2 3 cliques ab 1 and b 12 sharing b 1 form a 4 clique iff the non-shared vertex pair a 2 is an edge The 2 3 cliques ab 1 and bc 1 sharing b 1 form a 4 clique. b 1 2 1 b c a a 1 b 2 The 4 clique ab 12 and 3 clique bc 2 sharing b 2 form a 5 clique iff the non-shared vertex pair c 1 is an edge. The 4 clique abc 1 and 3 clique cd 1 sharing c 1 form a 5 clique c c d a a a b 2 5 clique abc 12 and 3 clique c 23 sharing c 2 form a 6 clique iff the non-shared vertex pairs a 3 and b 3 are edges. 5 clique abc 12 and 3 clique d 12 sharing vertices 1 and 2 form a 6 clique. 5 clique abcd 1 and 3 clique de 1 sharing edge e 1 form a 6 clique. b 2 c 3 d d e a a a 1 c d 3 b c 3 d c d 1 e 1 b 2 1 2 b 1 b c c a 1 2 1 b 6 clique abc 123 and 3 clique cd 3 sharing c 3 form a 7 clique iff the non-shared vertex pairs d 1 and d 2 are edges. 6 clique abc 123 and 3 clique d 23 sharing vertices 2 and 3 form a 7 clique iff vertex pair d 1 is an edge. 6 clique abcd 12 and 3 clique de 2 sharing edge d 2 form a 7 clique iff vertex pair e 1 is an edge 6 clique abcde 1 and 3 clique ef 1 sharing edge e 1 form a 7 clique. 1 b c d e f Although the pattern seems complex, the 2 PART Clique Algorithm can be stated: A Kclique and 3 clique sharing 2 vertices form a K+1 clique iff all edges from the non-shared 3 clique vertex to each non-shared Kclique vertex (from the other PART) exist. That is, check edge existence between all non-shared vertices.

Most bipartite graphs involve a subject part and an object part, e. g. , Most bipartite graphs involve a subject part and an object part, e. g. , women-events, Investors-Stocks, Customers-Items, Subject-Accessibility in the system access case. Most tripartite hypergraphs involve a subject, object and circumstance part, eg, Investor-Stock-Day, Customer-Item-Store, Subject-Accessibility-Day Most quadrapartite hypergraphs involve a subject, object and 2 circumstance parts, e. g. , Customer-Item-Store-Day. Most multi-partite hypergraphs can be realized as a subject-object bipartite graph with the circumstances as edge labels. A biclique is a complete subgraph of a bipartite graph (having every edge it is allowed to have and at least 1 (rules out the trivial case of no edges)). Every induced subgraph of a biclique is a biclique and therefore, we get the same downward closure: If two bicliques with k vertices each overlap in k-2 verticies and if the other two verticies form an edge, then the union of the two k-biciques is a (k+1)biclique. The only difference is that with bicliques, it is easier because we only need to check that the unshared pair is an edge when those two points are from different parts. Otherwise the union is a (k+1)biclique by default. p. Tree Bi. Clique Existence Thm (BCLQep) |W|=k. (W, EW) CLQk iff x, y W |Wx&Wy|=k-2 (k*(k-1)/2 ANDs) OR |W|=k. (W, EW) CLQk iff xy EW s. t. |Wx&Wy|=k-2 and u, v Wx&Wy u Wv (1 AND (but which one? ) and k-2 lookups). OR Bi. Clique Existence Thm (BCLQe) Let G=(S, O, E) be a bipartite graph and U S and V O with |U|=k and |V|=h then the induced subgraph, (U, V, EUV) BCLQk (is a k-biclique) iff every induced (k-1)vertex subgraph of (W, EW) CLQk-1. Clique Mining Thm (CLQm) finds all cliques using a closure property: Let Candk+1 Clique. Set CCLQk+1. By the CLQe thm, CCLQk+1= all s of CLQk-pairs having k-1 common vertices. Let C CCLQk+1 be a union of two k-cliques with k-1 common vertices. Let v and w be their kth (non-common) vertices respectively, then C CLQk+1 iff Evw=1 (Just check a single bit in PE. ) Clique Existence Thm edge count (CLQec): C={1, 2, 3, 4}, CU=C&EU. ct(CU)=comb(4, 2)=4!/2!2!=6 C CLQ 4. Is there an edge count Clique Mining Thm?