Version 1 9 2001 FINANCIAL ENGINEERING DERIVATIVES AND RISK MANAGEMENT

Version 1/9/2001 FINANCIAL ENGINEERING: DERIVATIVES AND RISK MANAGEMENT (J. Wiley, 2001) K. Cuthbertson and D. Nitzsche LECTURE Options Pricing BOPM 1

Topics • Pricing: One Period BOPM • Pricing: Two-Period BOPM • Delta Hedging © K. Cuthbertson, D. Nitzsche

Pricing: One Period BOPM © K. Cuthbertson, D. Nitzsche

Binomial Model • Pricing an option by creating a synthetic risk free portfolio of “stock + written call”. • Risk free, synthetic portfolio must earn the (known) risk free rate, r =5% - otherwise riskless arbitrage profits could be made. • One period call option (expires at t=1) with payoff max (ST - K, 0) © K. Cuthbertson, D. Nitzsche

Figure 3: Payoffs from the 1 -Period BOPM A. Long One Share (U=1. 1, D=0. 9) Su = SU = 110 100 Difference =20 Sd = SD = 90 B. Long One Call K = $ 100 Cu = 10 = (ST - K) C Difference =10 Cd = 0 Try : Long 1/2 share and write(sell) one call Hedge Ratio = 1/2 (=10 / 20) = Cu - Cd / Su - Sd

Portfolio =Long 1/2 share and write one call • Note: payoff to written(sold) call is “opposite” of long call • Up Vu = (0. 5) 110 - 10 = 45 • Down Vd = (0. 5) 90 - 0 = 45 • Hence we have a Risk free portfolio © K. Cuthbertson, D. Nitzsche

Portfolio =Long 1/2 share and write one call • Cost of risk free portfolio = (1/2) S - C • Portfolio must earn the risk free rate: (Value at t=1) / (Cost at t=0) = (1+r) 45 / [ (1/2) (100) - C)] = (1+r) • If r = 0. 05 = risk free rate • then “fair/corrrect/ no-arbitrage price, C = 7. 143 • Note: Cost of portfolio at t=0 for correctly priced call is (1/2) S - C = 50 - 7. 143= 42. 957 © K. Cuthbertson, D. Nitzsche

Overpriced Call Ca = 7. 5 • Can I make a riskless profit ? Overpriced call , therefore sell (write) the call AND go long (ie. Buy ) 1/2 share • Cost of strategy(t=0) = (1/2) S - Ca = 50 -7. 5= 42. 5 • Borrow 42. 5 from bank at r=5% to execute the strategy • Owe the bank at t=1 : 42. 5 (1. 05) • Value of your portfolio at t=1 “up” or “down”) • Net $ profit (at t=1) • Note: ( 0. 375/42. 5) = 0. 882 % © K. Cuthbertson, D. Nitzsche = $44. 625 = 45 (regardless of = $ 0. 375

Overpriced Call Ca = 7. 5 • Alternative presentation: • Cost of strategy(t=0) = 42. 5 • Value of your portfolio at t=1 = 45 (regardless of “up” or “down”) • Return = (45/42. 5)- 1 = 5. 882% • (ie. greater than r=5%, cost of borrowing from bank, or return on a riskless deposit in the bank) © K. Cuthbertson, D. Nitzsche

Under-priced Call Ca = 7. 0 • Can I make a riskless profit ? • Underpriced call , therefore buy the call • AND short sell 1/2 share • • • Receipts at t=0 = (1/2) S - Ca = 50 -7. 0= 43 Invest at r giving, at t=1, 43(1. 05) = 45. 15 Value ( t=1) = - 45 regardless of “up” or “down” (ie. You have to buy back the share and take the payoff from your long call) • Net profit = 45. 15 - 45 = $0. 15 • Return = 0. 15/43 - 1 = 0. 349% © K. Cuthbertson, D. Nitzsche

Complete Algebra • Vu = h. (SU) - Cu = Vd = h. (SD) - Cd • Hence • h =1/2 = ( Cu - Cd ) / (SU - SD) • Riskless Portfolio earns risk free rate of return: • [ Value at t=1 / Cost at t=0 ] = (1+r) Vu or Vd / [ h S - C)] = (1+r) C = (1 / R) [ q Cu +(1 -q) Cd ] • where q= [R - D] / ( U-D ) and R=(1+r) • q ~ risk neutral probability of “up” move © K. Cuthbertson, D. Nitzsche

Pricing: Two-Period BOPM © K. Cuthbertson, D. Nitzsche

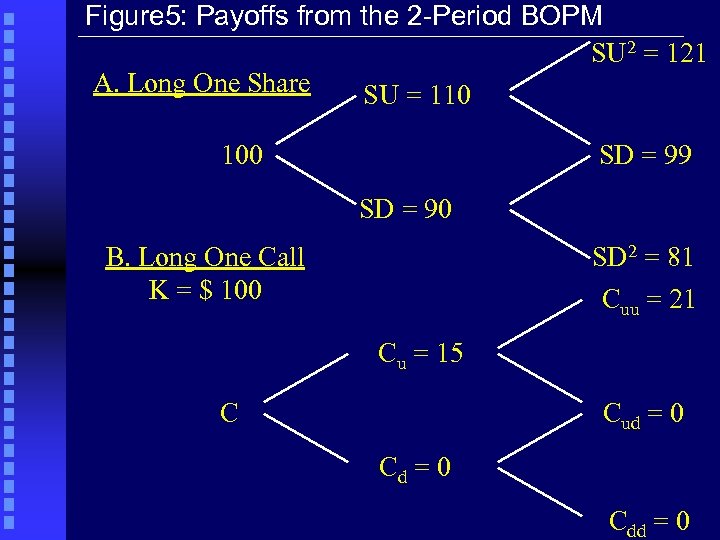Figure 5: Payoffs from the 2 -Period BOPM SU 2 = 121 A. Long One Share SU = 110 100 SD = 99 SD = 90 B. Long One Call K = $ 100 SD 2 = 81 Cuu = 21 Cu = 15 C Cud = 0 Cdd = 0

Figure 6 : Payoffs from the 2 -Period BOPM Option Value and Hedge Ratios Cuu = 21 C = 10. 715 (h = 0. 75) Cu = 15 (hu=0. 9545) Cud = 0 Cd = 0 (hd=0) Cdd = 0

Two Period : Algebra © K. Cuthbertson, D. Nitzsche

Delta Hedging with the (Two-period) BOPM © K. Cuthbertson, D. Nitzsche

Delta Hedging with the (Two-period) BOPM • At t=0 ( h = 0. 75, C = 10. 714, S=100) Write 1000 calls and buy 750 shares • Buy 750 shares @ 100 = $75, 000 • Write 1000 calls at 10. 714 = $10, 714 • Net investment = $64, 285 • Cu node ( hu =0. 9545, Cu = 15, S =110 ) • Value of portfolio Vu = 750 (110) – 1000(15) = $67, 500 • Return over period-1 = 674500/64, 285 = 1. 05 (5%) • New hedge ratio hu =0. 9545 = Ns / Nc © K. Cuthbertson, D. Nitzsche

Delta Hedging • New hedge ratio hu =0. 9545 = Ns / Nc : • Either, • or, the A)Write 1000 calls and hold 954. 5 shares B) Write 785. 7 calls (= 750/0. 9545) and hold ‘original’ 750 shares • ‘A’ involves increasing the number of shares held from 750 to 954. 5 (at a price of $110 per share) • ‘B’ appears to be the cheaper alternative since it involves buying back 214. 3 calls ( = 1, 000 – 785. 7) at Cu = 15 per contract. • Assume we take ‘B’. We do not increase our “own funds” in the hedge so we borrow the funds required at the risk free rate r = 5%. © K. Cuthbertson, D. Nitzsche

Delta Hedging • Case B) Buy back 214. 3 calls @ 15 = $3, 214 (= borrowed funds) • Case B): Cuu node ( Cu = 21, S =121, r= 0. 05 ) • Value of shares = 750 (121) = 90, 750 • Less call payoff = 785. 7 (21) = 16, 500 • Less loan outstanding 3, 214(1. 05) = 3, 375 • Value of portfolio Vuu(case B) = 70, 875 • Return over period-2(case B) = 70, 875/67, 500 = 1. 05 (5%) © K. Cuthbertson, D. Nitzsche

• Case-A: Outcome is again a return of 5%. • © K. Cuthbertson, D. Nitzsche

Figure 4 : Binomial Tree : Dividend Payments SU S SU 2(1 -d) SU(1 -d) SD SUD(1 -d) SD 2 (1 -d) Note: Dividend payments are proportional The tree still recombines

End of Slides © K. Cuthbertson, D. Nitzsche