Version 1 9 2001 FINANCIAL ENGINEERING DERIVATIVES AND RISK MANAGEMENT

Version 1/9/2001 FINANCIAL ENGINEERING: DERIVATIVES AND RISK MANAGEMENT (J. Wiley, 2001) K. Cuthbertson and D. Nitzsche LECTURE Derivatives: An Overview 1

Topics Forwards and Futures Contracts Options Contracts Swaps 2

Forwards and Futures 3

Forward/Futures Contract The buyer(long) in a forward/futures contract: uacquires a legal obligation to buy an asset (the underlying) ·at some specific future date (maturity/expiry date) ·in an amount (contract size). ·and at a price (the forward/futures price) which is fixed today. 4

Uses of Forward/Futures Contract Hedging (removing risk) In Jan. Mac. Donalds purchases a forward contract for delivery of live cattle in December at price fixed today ~ holds to maturity Speculation Buy a 3 m futures contract today at F 0 =$100 and sell after 1 m at F=$110 ~ close out contract (no delivery) and profit of $10. Arbitrage Keeps movement of F in line with S (underlying) 5

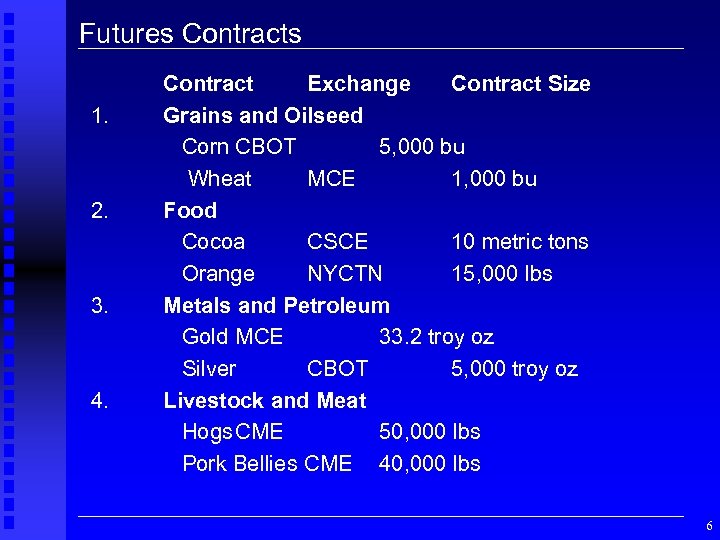Futures Contracts 1. 2. 3. 4. Contract Exchange Contract Size Grains and Oilseed Corn CBOT 5, 000 bu Wheat MCE 1, 000 bu Food Cocoa CSCE 10 metric tons Orange NYCTN 15, 000 lbs Metals and Petroleum Gold MCE 33. 2 troy oz Silver CBOT 5, 000 troy oz Livestock and Meat Hogs CME 50, 000 lbs Pork Bellies CME 40, 000 lbs 6

Futures Contracts 6. Contract Size Swiss Franc CME Euro CME Japanese Yen 12. 5 m 5. Contract Exchange Foreign Currency British Pound IMM SFr 125, 000 Euro 125, 000 Stock Indices S&P 500 £ 62, 500 CME IOM $500 x Value Line KCBT $500 x FTSE 100 LIFFE £ 10 x Index index Eurotop 100 LIFFE Euro 20 x index 7

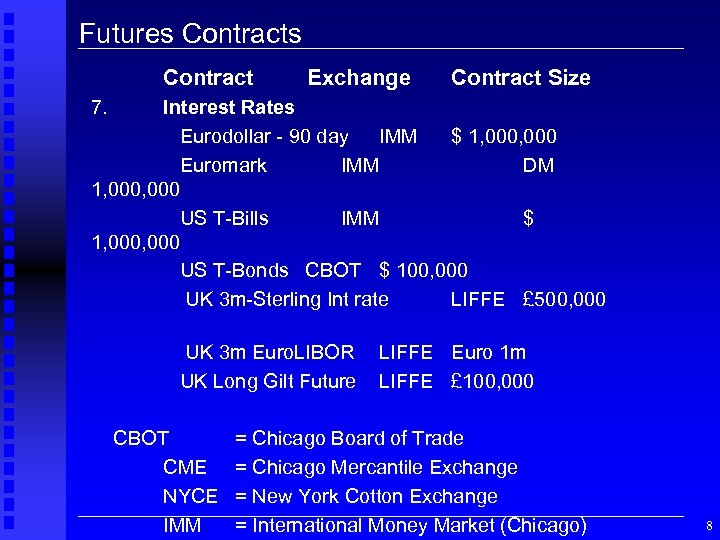Futures Contract Exchange Contract Size 7. Interest Rates Eurodollar - 90 day IMM $ 1, 000 Euromark IMM DM 1, 000 US T-Bills IMM $ 1, 000 US T-Bonds CBOT $ 100, 000 UK 3 m-Sterling Int rate LIFFE £ 500, 000 UK 3 m Euro. LIBOR UK Long Gilt Future CBOT CME NYCE IMM LIFFE Euro 1 m LIFFE £ 100, 000 = Chicago Board of Trade = Chicago Mercantile Exchange = New York Cotton Exchange = International Money Market (Chicago) 8

Comparison of Forwards and Futures FORWARDS Private contract Delivery at expiry FUTURES Traded on an exchange Usually closed out before maturity Usually one delivery date Range of delivery dates No cash paid until expiry Cash payments Daily( margin) Negotiable choice of delivery dates, size of contract Standardised Contract 9

Options Contracts 10

Options Holder has the right to buy or sell an ‘asset’ (underlying) at some time in the future at a fixed price but she does not have to exercise this right can ‘walk away’ from the contract if holder wishes ~ latter is key distinction between options and futures/futures contracts. E. g. In Jan, purchase an option to buy 100 Microsoft shares in September, at a fixed price of $102 What happens in Sept if actual stock price is $90 or $110? 11

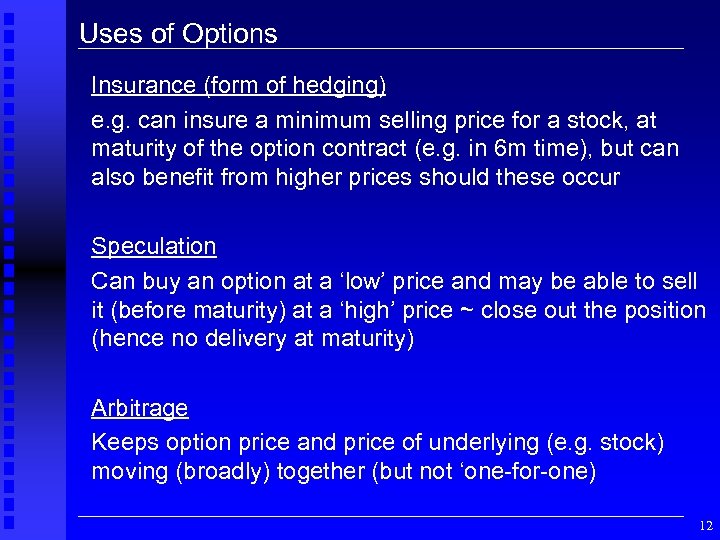Uses of Options Insurance (form of hedging) e. g. can insure a minimum selling price for a stock, at maturity of the option contract (e. g. in 6 m time), but can also benefit from higher prices should these occur Speculation Can buy an option at a ‘low’ price and may be able to sell it (before maturity) at a ‘high’ price ~ close out the position (hence no delivery at maturity) Arbitrage Keeps option price and price of underlying (e. g. stock) moving (broadly) together (but not ‘one-for-one) 12

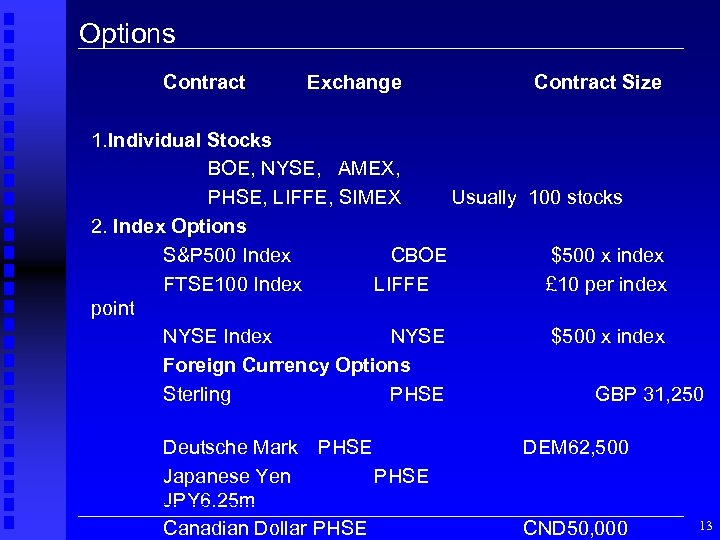Options Contract Exchange Contract Size 1. Individual Stocks BOE, NYSE, AMEX, PHSE, LIFFE, SIMEX Usually 100 stocks 2. Index Options S&P 500 Index CBOE $500 x index FTSE 100 Index LIFFE £ 10 per index point NYSE Index NYSE $500 x index Foreign Currency Options Sterling PHSE GBP 31, 250 Deutsche Mark PHSE Japanese Yen PHSE JPY 6. 25 m Canadian Dollar PHSE DEM 62, 500 CND 50, 000 13

Options Contract Exchange Contract Size 3. Options on Futures Contracts Options on interest rate futures: Eurodollars IMM $1 m US T-Bills IMM $1 m US T-Bond CBOT $100, 000 3 -month Euro. LIBOR LIFFE as for futures UK Long Gilt LIFFE as for futures Options on index futures: S&P 500 Index IOM $500 x premium Nikkei 225 IOM $5 x premium Most commodities (agriculture and metals) on which there are futures contracts (see above). CBOT, CME, KCBT, COMEX, CTN The same as in the futures contract 14

Call Option A European call option gives the holder (the long) the right (but not an obligation) ·to purchase the underlying asset at a ·specified future date (known as the expiration, expiry or maturity date) ·for a certain price (the exercise or strike price) ·and in an amount (contract size) which is fixed in advance. ·For this privilege you pay today, the call premium/price. 15

Figure 1. 1 : Buy one European Call Option Strike price K = $80 Profit $5 K = $80 0 Call premium $83 $88 -$3 © K. Cuthbertson, D. Nitzsche ST

Figure 1. 8 : Leverage from option (on 100 shares) OPTIONS MARKET (JULY) CASH MARKET (JULY) Call premium, C = $3 Premium paid = $300 Strike price, K = $80 Spot price, S = $78 Cash paid = $7800 OPTIONS MARKET (OCT. ) CASH MARKET (OCT. ) Profit = $8 = ($88 - $80) Net profit = $800 - $300 Return = $500/$300 = 167% Profit = $10 = ($88 - $78) Total profit = $1000 Return = $1000/$7800 = 12. 8% © K. Cuthbertson, D. Nitzsche

Figure 1. 2 : Sell (write) a European Call Option Strike price K = $80 Profit $3 Call premium 0 $83 K = $80 -$5 © K. Cuthbertson, D. Nitzsche $88 ST

Put Option A European put option gives the holder (the long) the right (but not an obligation) ·to sell the underlying asset at a ·specified future date (known as the expiration, expiry or maturity date) ·for a certain price (the exercise or strike price) ·and in an amount (contract size) which is fixed in advance. ·For this privilege you pay today, the call premium/price. 19

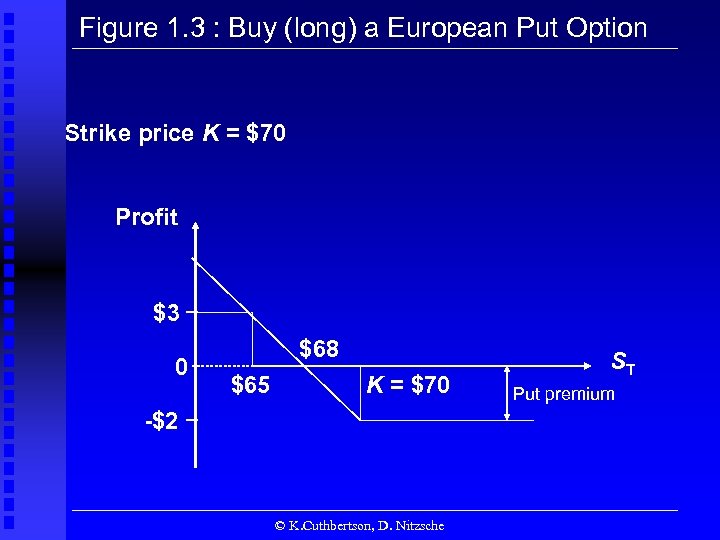Figure 1. 3 : Buy (long) a European Put Option Strike price K = $70 Profit $3 0 $68 $65 K = $70 -$2 © K. Cuthbertson, D. Nitzsche ST Put premium

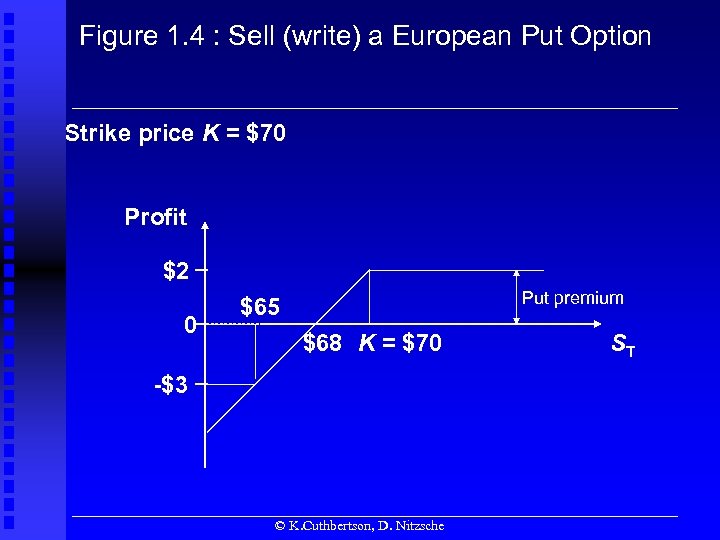Figure 1. 4 : Sell (write) a European Put Option Strike price K = $70 Profit $2 0 Put premium $65 $68 K = $70 -$3 © K. Cuthbertson, D. Nitzsche ST

Swaps © K. Cuthbertson, D. Nitzsche

Figure 1. 5 : Liabilities : Using Swaps Swap A negotiated (OTC) agreement between two parties to exchange cash flows at a set of pre-specified future dates Plain Vanilla Interest Rate Swap M/s A. agrees to pay interest at a floating rate and receive fixed rate payments from the “other side” of the swap transaction (eg. M/s B) e. g. 5 year swap, with floating rate at 6 m LIBOR, with resets every 6 months. Fixed rate is say 5% p. a. Usually the interest payments are in the same currency © K. Cuthbertson, D. Nitzsche

Figure 1. 5 : Liabilities : Using Swaps Floating to Fixed: Liability LIBOR + 0. 5% LIBOR Issue Floating Rate Bond Firm’s Swap 6% fixed Net Payment = 0. 5% + 6% = 6. 5% (fixed) Fixed to Floating : Liability 6. 2% fixed 6% fixed Issue Fixed Rate Bond Firm’s Swap Net Payment = 0. 2% + LIBOR (floating) © K. Cuthbertson, D. Nitzsche LIBOR

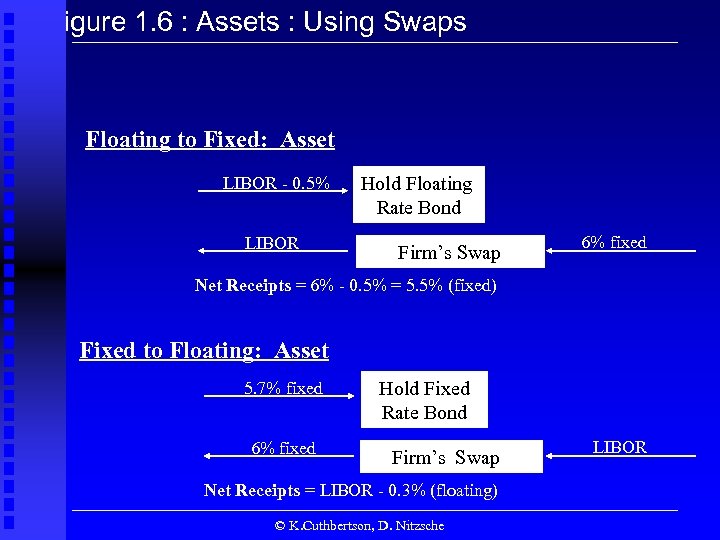Figure 1. 6 : Assets : Using Swaps Floating to Fixed: Asset LIBOR - 0. 5% LIBOR Hold Floating Rate Bond Firm’s Swap 6% fixed Net Receipts = 6% - 0. 5% = 5. 5% (fixed) Fixed to Floating: Asset 5. 7% fixed 6% fixed Hold Fixed Rate Bond Firm’s Swap Net Receipts = LIBOR - 0. 3% (floating) © K. Cuthbertson, D. Nitzsche LIBOR

Figure 1. 7 : Swap : financial intermediary 12% fixed Hold Floating Rate Bond LIBOR - 1% Without swap if LIBOR > 13% firm’s swap makes a loss. 11% fixed Firm’s Swap LIBOR After swap : Net Receipts = (12% - 11%) + LIBOR - (LIBOR - 1%) = 2% (fixed) © K. Cuthbertson, D. Nitzsche

End of Slides © K. Cuthbertson, D. Nitzsche