Вероятностные оценки погрешностей n В результате измерения

Вероятностные оценки погрешностей n В результате измерения получают значение измеряемой величины в виде числа в принятых единицах величин. n Погрешность измерения тоже выражается в виде числа. n Погрешность измерения является случайной величиной, описывающимся законом распределения погрешностей. 1/31/2018 1

n Из теории вероятности известно, что закон распределения характеризуется числовыми характеристиками (неслучайными числами), которые и используются для количественной оценки погрешности. Основными числовыми характеристиками законов распределения являются: М [∆x] - математическое ожидание D [∆x] – дисперсия 1/31/2018 2

Математическое ожидание погрешности измерений есть неслучайная величина, относительно которой рассеиваются другие значения погрешностей при повторных измерениях. -функция распределения Математическое ожидание характеризует систематическую составляющую погрешности измерения, , т. е. это тоже самое, что m. Как числовая характеристика погрешности М[∆x] показывает на смещение результатов измерения относительно истинного значения измеряемой величины. 1/31/2018 3

Дисперсия погрешности D[∆x] Она характеризует степень разброса отдельных значений погрешности относительно математического ожидания. 1/31/2018 4

Так как рассеивание происходит за счет случайной составляющей погрешности, то Чем D меньше, тем меньше разброс, тем точнее выполнены измерения. Следовательно дисперсия может служить характеристикой точности проведенных измерений. Однако, дисперсия выражается в единицах погрешности в квадрате. 1/31/2018 5

Поэтому, в качестве числовой характеристики точности измерений используют среднее квадратичное отклонение с положительным знаком и выражаемое в единицах погрешности. Обычно, при проведении измерений стремятся получить результат измерения с погрешностью, не превышающей допустимое значение. Знание только одного среднеквадратического отклонения не позволяет найти максимальную погрешность, которая может встретиться при измерениях, что свидетельствует об ограниченных возможностях такой числовой характеристики 1/31/2018 6

При разных условиях измерения, когда законы распределения погрешностей могут отличаться друг от друга, погрешность с меньшей дисперсией может принимать большие значения. Максимальные значения погрешности зависят не только от , но и от вида закона распределения. Тогда распределение погрешности теоретически не ограниченно, и, например, при нормальном распределении, погрешность может быть любой по значению. В этом случае можно говорить лишь об интервале, за границы которого погрешность не выйдет с некоторой вероятностью. Этот интервал называют доверительным интервалом, характеризующим его вероятность – доверительной вероятностью, а границы этого интервала – доверительными значениями погрешности. 1/31/2018 7

Правило 3 В практике измерений применяют различные значения доверительной вероятности PД, например: 0. 90; 0. 95; 0. 98; 0. 9973 и 0. 999. Доверительный интервал и доверительную вероятность выбирают в зависимости от конкретных условий измерений. Так например, при нормальном законе распределения случайных погрешностей со средним квадратическим отклонением часто пользуются доверительным интервалом от + до - 1/31/2018 8

Для которого доверительная вероятность равна Р = 0. 9973. Такая доверительная вероятность означает, что в среднем из 370 случайных погрешностей только одна погрешность по абсолютному значению будет больше, т. е. 370/371= 0. 9973. Так как на практике число отдельных измерений редко превышает несколько десятков, то появление даже одной случайной погрешности, больше, чем маловероятное событие, наличие же двух подобных погрешностей почти невозможно. 1/31/2018 9

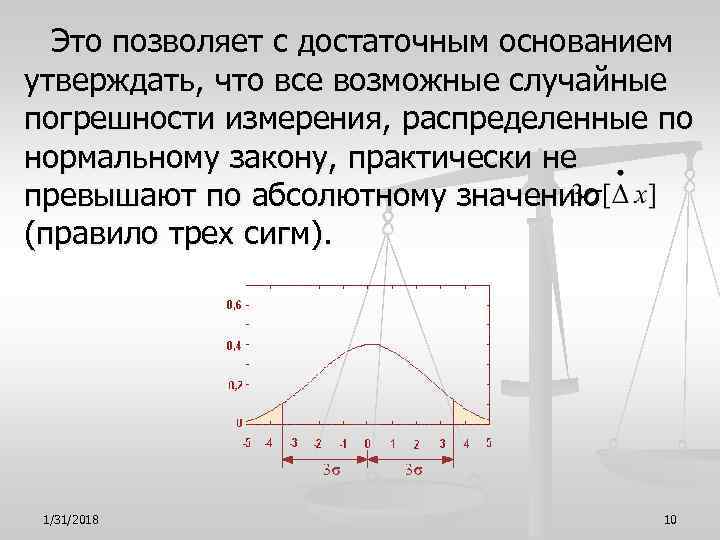Это позволяет с достаточным основанием утверждать, что все возможные случайные погрешности измерения, распределенные по нормальному закону, практически не превышают по абсолютному значению (правило трех сигм). 1/31/2018 10

Правило трех сигм 3 -sigma rule n Вероятность того, что случайная величина отклонится от своего математического ожидания на большую величину, чем утроенное среднее квадратичное отклонение, практически равна нулю. Правило справедливо только для случайных величин, распределенных по нормальному закону. n Например, пусть имеется выборка наблюдений за ежедневными продажами в магазине. Значения их распределены по нормальному закону с математическим ожиданием 150 000 руб. и среднеквадратическим отклонением 20 000 руб. Тогда в соответствии с правилом 3 -х сигм продажи ниже, чем 150 000 - 20 000 x 3 = 90 000, и выше, чем 150 000 + 20 000 х 3 = 210 000, являются практически невозможными событиями. Фактически это означает, что рассматривать данные объемы продаж как потенциально возможные не имеет смысла. 1/31/2018 11

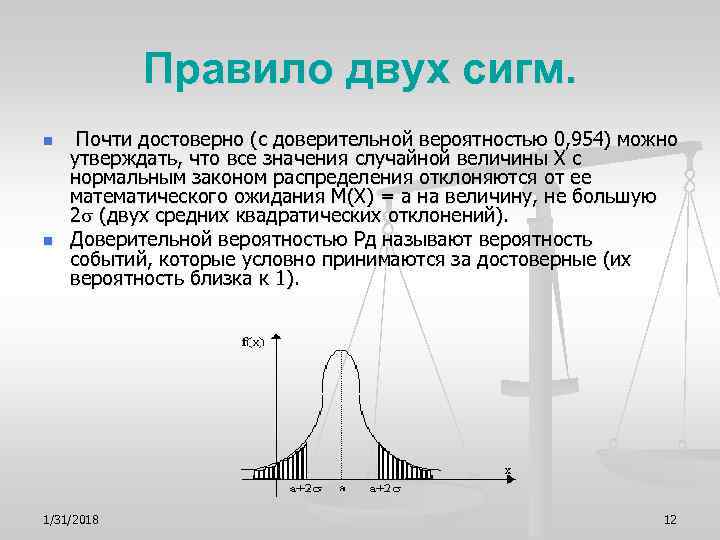Правило двух сигм. n Почти достоверно (с доверительной вероятностью 0, 954) можно утверждать, что все значения случайной величины X с нормальным законом распределения отклоняются от ее математического ожидания M(X) = a на величину, не большую 2 (двух средних квадратических отклонений). n Доверительной вероятностью Pд называют вероятность событий, которые условно принимаются за достоверные (их вероятность близка к 1). 1/31/2018 12

1/31/2018 13

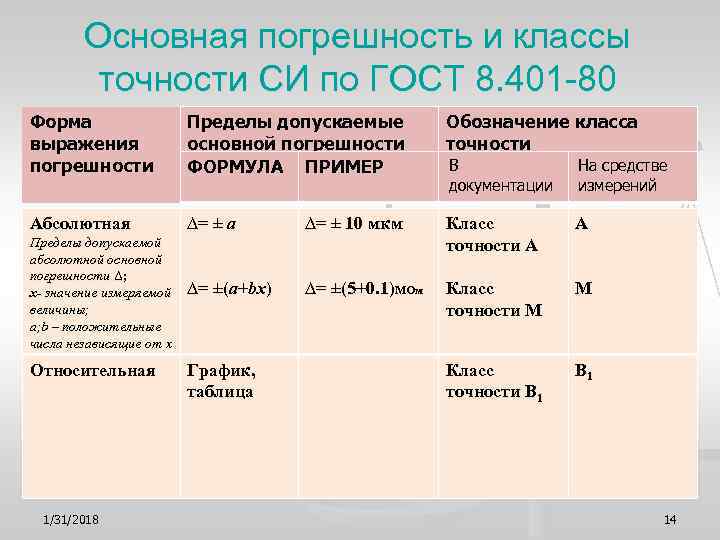Основная погрешность и классы точности СИ по ГОСТ 8. 401 -80 Форма Пределы допускаемые Обозначение класса выражения основной погрешности точности погрешности ФОРМУЛА ПРИМЕР В На средстве документации измерений Абсолютная ∆= ± а ∆= ± 10 мкм Класс А Пределы допускаемой точности А абсолютной основной погрешности Δ; x- значение измеряемой ∆= ±(а+bx) ∆= ±(5+0. 1)МОм Класс М величины; точности М a; b – положительные числа независящие от x Относительная График, Класс В 1 таблица точности В 1 1/31/2018 14

1/31/2018 15

1/31/2018 16

1/31/2018 17

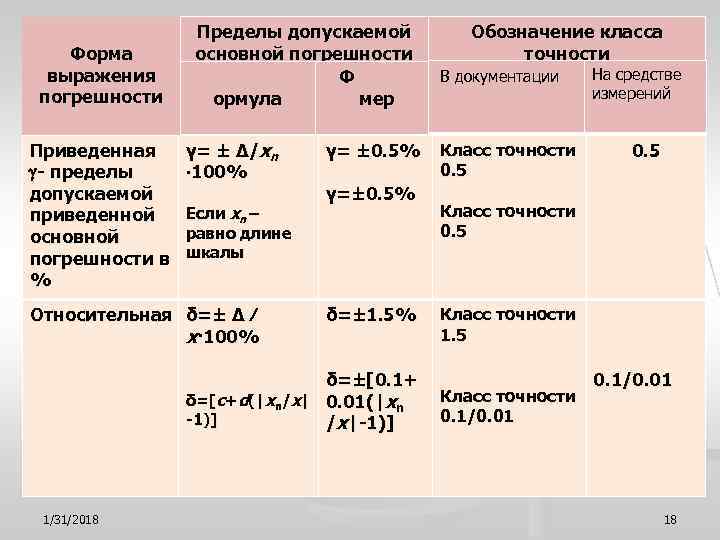Пределы допускаемой Обозначение класса Форма основной погрешности точности выражения Ф При В документации На средстве погрешности ормула мер измерений Приведенная γ = ± ∆/ x n γ= ± 0. 5% Класс точности 0. 5 - пределы ∙ 100% 0. 5 допускаемой γ=± 0. 5% приведенной Если xn – Класс точности основной равно длине 0. 5 погрешности в шкалы % Относительная δ=± ∆ ⁄ δ=± 1. 5% Класс точности x· 100% 1. 5 δ=±[0. 1+ 0. 1/0. 01 δ=[c+d(|xn/x| 0. 01(|xn Класс точности -1)] /x|-1)] 0. 1/0. 01 1/31/2018 18

1/31/2018 19

1/31/2018 20

1/31/2018 21

1/31/2018 22

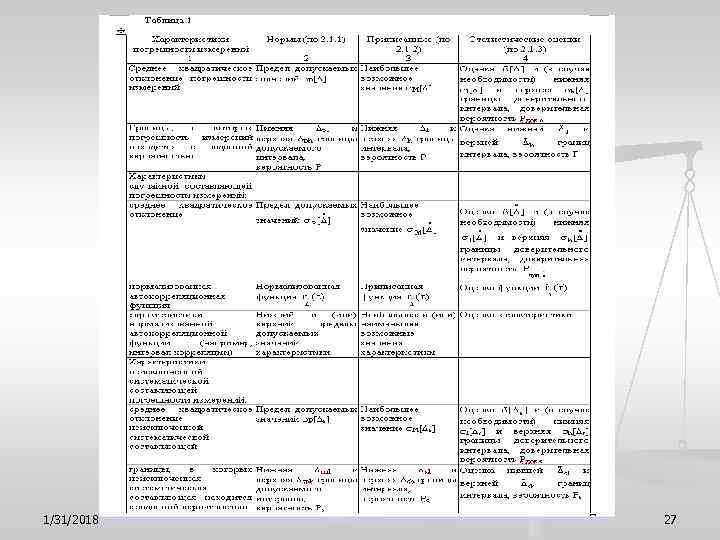
В соответствие с ГОСТом 8. 011 -72 доверительный интервал является одной из основных характеристик точности измерений. x, Δx от xn до x. B ; P Δx xn - погрешность измерений с нижней и верхней ее границами в тех же единицах. x. B Х - результат измерения в единицах измеряемой величины Р – вероятность с которой погрешность измерения находиться в этих границах. Пример : (1, 03± 0, 04) В; Р=1. 1/31/2018 23

Примером записи номинальной погрешности является указание класса точности электроизмерительного прибора. Для средств измерений, пределы допускаемых погрешностей которых выражают в виде относительных или приведенных погрешностей в ГОСТе установлен следующий ряд чисел для выражения пределов допускаемых погрешностей и применяемых для обозначения класса точности. 1· 10 n ; 1. 5· 10 n ; 2. 5· 10 n ; 4· 10 n; 5· 10 n ; 6· 10 n , где n=1; 0; -2 и т. д. 1/31/2018 24

С использованием чисел указанного ряда разработаны условные обозначения классов точности. Ряды классов точности устанавливают в государственных стандартах на отдельные виды средств измерений С точки зрения вероятностного характера погрешности делятся на : Систематические и случайные. Систематическими называют погрешности, которые вызываются постоянно действующими факторами. 1/31/2018 25

n В настоящее время ГОСТ 8. 011 -72 заменен на МИ 1317 -2004 разработанный Федеральным государственным унитарным предприятием Всероссийский научно- исследовательский институт метрологической службы (ФГУП ВНИИМС). 1/31/2018 26

1/31/2018 27

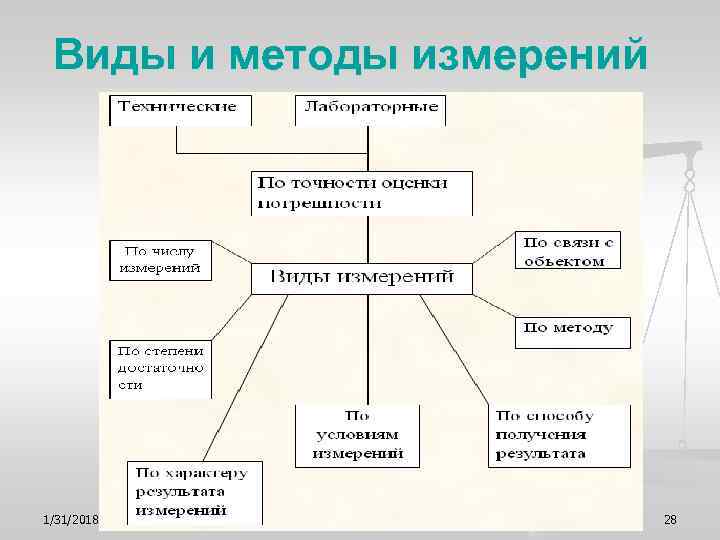Виды и методы измерений 1/31/2018 28