Вероятностно статистический подход Классическое определение вероятности

Вероятностно – статистический подход

Классическое определение вероятности P(A) = m / n, (1) где P(A) — вероятность события A; m — число случаев, благоприятствующих событию A; n — общее число случаев. Пример. При бросании игрального кубика возможно 6 исходов — выпадение одной из граней с номером 1, 2, 3, 4, 5 или 6. Какова вероятность выпадения грани с четным номером? Решение. Все n = 6 исходов образуют группу событий и равновозможны, т. е. единственно возможны, несовместны и равновозможны. Событию A — «появление грани с четным номером» — благоприятствуют 3 исхода — 2, 4 и 6. Тогда P(A) = 3/6 = 1/2.

Статистическое определение вероятности P(A) = m / n, (2) где P(A) — статистическая вероятность события A; m — число испытаний, в которых появилось событие A; n — общее число испытаний. . Свойства вероятности 1. Вероятность любого события заключается между нулем и единицей, т. е. 0 ≤ P(A) ≤ 1. 2. Вероятность достоверного события равна единице, т. е. P(Ω) = 1. 3. Вероятность невозможного события равна нулю, т. е. P( ) = 0. 4. Сумма вероятностей полной группы событий равна единице. События, вероятности которых очень малы (близки к нулю) или очень велики (близки к единице), называют практически невозможными или практически достоверными.

Задача 1 В непрозрачном мешочке находятся 32 шара, окрашенных в различные цвета. Определить количество информации о цвете наугад взятого из мешочка шара. Решение При реализации этого события возможен один из 32 исходов, соответствующий одному из 32 цветов. Значит, вероятность события равна 1/32. Задача 2 В непрозрачном мешочке содержатся 32 шара, окрашенных в различные цвета. Определить количество информации в сообщении, что из мешочка достали шар. Решение Так как ничего, кроме шара, из мешочка взять невозможно, то вероятность данного (достоверного) события равна 1. В каком случае событие несет больше информации? Очевидно, если мы заранее знаем, что в мешочке лежат только шары, то сообщение о том, что мы достали шар, никакой новой информации не дает. Вообще, чем меньше вероятность события, тем больше информации несет сообщение о том, что такое событие все-таки произошло.

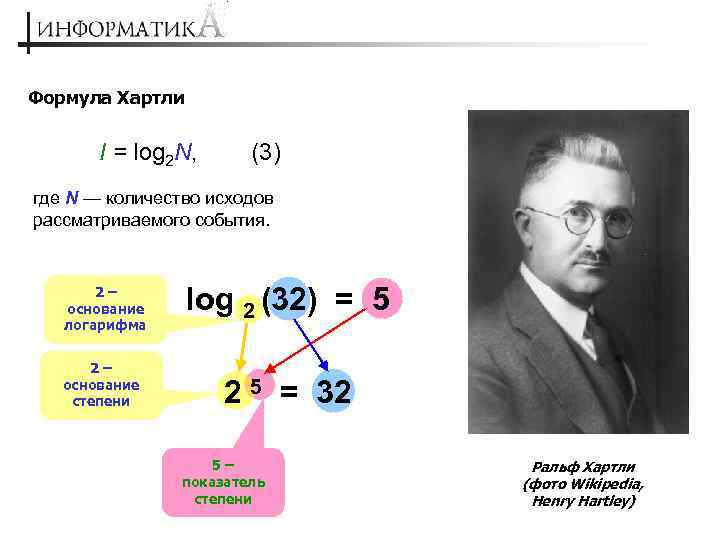Формула Хартли I = log 2 N, (3) где N — количество исходов рассматриваемого события. 2– основание логарифма 2– основание степени log 2 (32) = 5 2 5 = 32 5– показатель степени Ральф Хартли (фото Wikipedia, Henry Hartley)

Основные свойства логарифма 1. log(1) = 0, так как любое число в нулевой степени дает 1. 2. log(ab) = b · log(a). 3. log(a · b) = log(a) + log(b). 4. log(a/b) = log(a) − log(b). 5. log(1/b) = 0 − log(b) = − log(b). Если сообщение частично снимает неопределенность события, то количество информации в нем можно определить по формуле: I = log 2(Nдо/Nпосле), (4) где Nдо — количество альтернативных исходов до сообщения, Nпосле — количество альтернативных исходов после сообщения

Единица измерения информации – бит Название bit (бит) образовано из двух начальных и из последней букв английского выражения binary unit – «двоичная единица» , или, по другой версии, binary digit – «двоичная цифра» . Да Нет Один бит соответствует выбору одной из двух возможностей (Да/Нет, 1 / 0 и т. д. ). Один бит соответствует количеству информации о событии, которое имеет вероятность ½. При бросании игрального кубика может равновероятно выпасть одна из 6 граней (вероятность выпадения. например, шестерки равна 1/6). Тогда количество информации в сообщении о том, что выпала «шестерка» , равно log 2(6) = 2, 585 бит (в отличие от использования понятия «бит» в компьютерной технике здесь допустимо дробное количество битов).

«Неправильный» игральный кубик Пусть игральный кубик имеет одну грань с 1 точкой, две грани с 2 точками и три грани с 3 точками. Каковы вероятности выпадения при его бросании 1, 2 и 3 точек? Перечислим возможные события: {1, 2, 2, 3, 3, 3}. Вероятность выпадения « 1» : p 1 = n 1/N = 1/6 = 0, 1667. Вероятность выпадения « 2» : p 2 = n 2/N = 2/6 = 0, 3333. Вероятность выпадения « 1» : p 3 = n 3/N = 3/6 = 0, 5000. Сумма всех вероятностей в точности равна 1 (что очевидно: хоть одно из этих событий произойдет обязательно). Как в этом случае определить количество информации о выпадении какого-либо количества точек?

Вычисление количества информации путем разбиения на подмножества «неправильная» рулетка, на которой из каждых 16 Пусть имеется «запусков» 2 раза выпадает единица, 2 раза – двойка, 4 раза – тройка и 8 раз – четверка. Тогда весь набор событий можно записать так: {1, 1, 2, 2, 3, 3, 4, 4, 4, 4} Вероятности этих событий: p 1 = n 1/N = 2/16 = 0, 125 p 2 = n 2/N = 2/16 = 0, 125 p 3 = n 3/N = 4/16 = 0, 250 p 4 = n 4/N = 8/16 = 0, 500 Количество информации о выпадении « 1» : I 1 = log 2(2/16) = log 2(8) = 3 бита. Количество информации о выпадении « 2» : I 2 = log 2(2/16) = log 2(8) = 3 бита. Количество информации о выпадении « 3» : I 3 = log 2(4/16) = log 2(4) = 2 бита. Количество информации о выпадении « 4» : I 4 = log 2(8/16) = log 2(2) = 1 бит. 4 Общее количество информации для определения одного из событий: = II= p 1*I 1 + p 2*I 2 * p 3*I 3 + p 4*I 4 + 0, 125*3 + 0, 25*4 + 0, 5*1 = 1, 75 бита. * + + + * = *

Неопределенность (энтропия) Чем больше возможно разных событий (исходов) и меньше вероятность совершения каждого события в повторяющемся опыте, тем больше изначальная неопределенность. Проведение опыта снимает эту неопределенность. Если возможно k исходов, то функция неопределенности f(k): • если k = 1, то f(k)=0 (т. е. неопределенности нет); • для двух независимых опытов a и b неопределенность их одновременного проведения (ab) равна сумме неопределенностей каждого опыта в отдельности (f(ab) = f(a) + f(b)). f(k) – это логарифмическая функция: Основание логарифма – любое. • log(1) = 0; Переход между системами логарифмов: • log(ab) = log(a) + log(b). loga(k) logb(k) = logb(a) · loga(k) константа log 2(k) — бит, log 10(k) — дит, ln(k) — нат

Неопределенность (энтропия) для разновероятных исходов Задача. В урне находятся 16 шаров, из них 2 шара красного цвета, 4 шара зеленого цвета и 10 шаров белого цвета. Вероятности: • для красных шаров: pк = 2/16, • для зеленых шаров: pз = 4/16, • для белых шаров: pб = 10/16. Функция неопределенности: f(pк, pз, pб) Энтропия вероятностей по Шеннону: Н = −K · Σpi · log(pi) константа Н = –Σpi · log(pi) – энтропия множества вероятностей p 1…pk. К чему относится минус? – (pi · log(pi)) = pi · – log(pi) = pi · log(pi – 1) = pi · log(1/pi). вероятность не может быть отрицательной

Неопределенность (энтропия) для событий с равной вероятностью Формула Шеннона: Н = –Σpi · log(pi) Если всего возможно N исходов, из которых количество исходов i-го вида равно mi, то pi = mi/N. Тогда: Н = –Σpi · log(pi) = –Σ(mi/N) · log(mi/N) = = Σ(mi/N) · log(N/mi). Для N равновероятных событий все pi = 1/N, тогда: Н = –Σpi · log(pi) = –Σ 1/N · log(1/N) = = Σ 1/N · log(N) = N * 1/N · log(N) Н = log(N). значение энтропии по формуле Хартли Вывод: формула Хартли представляет собой частный случай формулы Шеннона. Клод Шеннон (фото www. bell-labs. com)

Неопределенность (энтропия) для маловероятных событий Формула Шеннона: Н = –Σpi · log(pi) Совершение события с очень малой вероятностью несет в себе большое количество информации. А какой вклад оно вносит в энтропию вероятностей? Пусть вероятность i-го исхода p = 1/2 n. Тогда log(1/p) = n, а p · log(1/p) = n/2 n. С ростом n знаменатель растет гораздо быстрее, поэтому при p → 0 произведение p · log(1/p) неограниченно убывает: lim(p·log(1/p)) = 0 p→ 0 Вывод. Маловероятные исходы вносят незначительный вклад в величину энтропии (неопределенности) рассматриваемого события. При значениях вероятности, близких к нулю, такими исходами можно пренебречь.

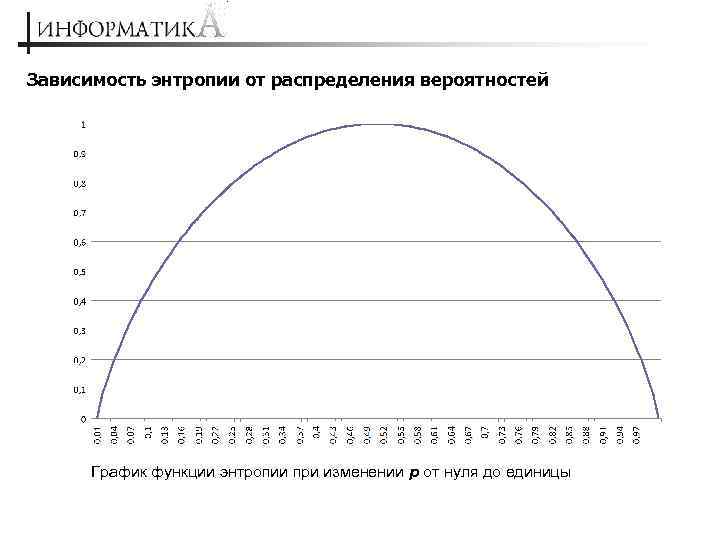Зависимость энтропии от распределения вероятностей График функции энтропии при изменении p от нуля до единицы

Решение задач Задача 1. Количество бит информации в сообщении «Миша на олимпиаде по информатике занял одно из 16 мест» равно 3, 5, 4, 2 или 424 бита? Решение Событием в данной задаче является конкретное место, занятое на олимпиаде (одно из 16). Сообщение же о том, что Миша вообще занял какое-то одно из мест, для нас неопределенность не уменьшает, и следовательно, информации не несет (т. е. несет 0 бит информации). Значит, среди представленного списка значений правильный ответ отсутствует.

Решение задач Задача 2. В озере обитают 12 500 окуней, 25 000 пескарей, а карасей и щук по 6250. Какое количество информации несет сообщение о ловле рыбы каждого вида? Сколько информации мы получим, когда поймаем какую-нибудь рыбу? Решение Обозначим: Ко = 12 500; Кп = 25 000; Кк = Кщ = 6250. 1. Общее количество рыбы: N = Ко + Кп + Кк + Кщ = 50 000. 2. Вероятности ловли каждого вида рыбы: pо = Ko/N = 12 500/50 000 = 0, 250 pп = Kп/N = 25 000/50 000 = 0, 500 pк = Kк/N = 6250/50 000 = 0, 125 pщ = Kщ/N = 6250/50 000 = 0, 125 3. Количество информации о ловле рыбы каждого вида: Iо = log 2(1/pо) = log 2(50 000 / 12 500) = log 2(4) = 2 бита Iп = log 2(1/pп) = log 2(50 000 / 25 500) = log 2(2) = 1 бит Iк = log 2(1/pк) = log 2(50 000 / 6250) = log 2(8) = 3 бита Iщ = log 2(1/pщ) = log 2(50 000 / 6250) = log 2(8) = 3 бита 4. Количество информации о ловле рыбы любого вида: I = –(pо ∙ log 2(pо) + pп ∙ log 2(pп) + pк ∙ log 2(pк) + pщ ∙ log 2(pщ)) = = 0, 250 ∙ 2 + 0, 500 ∙ 1 + 0, 125 ∙ 3 = 1, 750 бита

Решение задач Правильно ли полученное решение? 1. Так как заранее известно, что ловится рыба, то сообщение «выловлена рыба любого вида» не несет для нас информации, следовательно I = 0 бит. 2. Неопределенность (мера незнания) того, какой из четырех видов рыб выловлен, равна 1, 75 бит. Любое сообщение о вылове окуня, пескаря, карася или щуки снимает эту неопределенность. Следовательно, каждое такое сообщение несет информацию в 1, 75 бит и не более.

Решение задач Задача 3. Словарь аборигенов племени Мумбо-Юмбо содержит слова трех частей речи: существительные, глаголы и междометия. Абориген произносит предложение, состоящее из одного равновероятно выбранного из словаря слова. Количество информации, содержащееся в сообщении «Предложение состоит из глагола» , равно log 211 – log 23 бита. Информационный объем сообщения «Предложение состоит не из существительного» равен 2 – log 23 бита. В словаре только 21 междометие. Чему равно количество слов в словаре, которые не являются существительными? Решение Обозначения: N — общее количество слов; nс — количество существительных; nг — количество глаголов; nм — количество междометий. Сообщение, что предложение состоит из глагола, частично снимает неопределенность из N реализаций до неопределенности из nг реализаций, тогда: log 2(N/nг) = log 2(11) – log 2(3). Тогда: log 2(N/nг) = log 2(11/3), откуда N/nг = 11/3 или 3 · N = 11 · nг.

Решение задач Задача 3. Решение (продолжение) Сообщение, что предложение состоит не из существительного, также снимает неопределенность из N реализаций до неопределенности из (nг + nм) реализаций: log 2(N/(nг + nм)) = 2 – log 2(3) Тогда: log 2(N/(nг + nм)) = log 2(4) — log 2(3) или log 2(N/(nг + nм)) = log 2(4/3), откуда N/(nг + nм) = 4/3 или 3 · N = 4 · (nг + nм). По условию задачи nм = 21, тогда 3 · N = 4 · nг + 84. Построим систему уравнений: 3 · N = 4 · nг + 84 (1) 3 · N = 11 · nг (2) Вычитая из (2) выражение (1), получим: 7 · nг = 84, откуда nг = 84/7 = 12. Вывод: словарь аборигенов содержит 12 глаголов. Подставляя это значение в (2), получим: N = 11 · 12/3 = 44. Вывод: всего в словаре 44 слова, из них не существительных – nг + nм = 12 + 21 = 33. Ответ. В словаре аборигенов 33 слова, которые не являются существительными.

Формула Шеннона и двоичные коды Какое минимальное количество двоичных знаков можно использовать для кодирования символов текста? К. Шеннон в 1950 г. в статье «Современные достижения теории связи» показал, что не существует метода кодирования символов национального алфавита, использующего в среднем на 1 символ двоичных кодов меньше, чем значение H. Пример Пусть язык состоит из четырех букв: A, B, C и D с вероятностями 1/2, 1/4, 1/8 и 1/8. Самый простой код для них: A − 00, B — 01, C − 10, D — 11 (два двоичных знака на букву). Можно сконструировать более компактный код: A − 0, B — 10, C − 110, D — 111. Число использованных двоичных знаков здесь в среднем меньше. Его можно вычислить так: 1/2(1) + 1/4(2) + 1/8(3) = 1 · 3/4, где первый член относится к букве A, которая встречается в половине случаев и которой соответствует один двоичный знак, и т. д. Но 1 · 3/4 – это в точности значение H, вычисленное как энтропия вероятностей.