Вероятность Виды распределения Всякий результат полученный в

Вероятность. Виды распределения.

Всякий результат, полученный в процессе наблюдения или эксперимента, называют событием Событие, которое может произойти, а может и не произойти, называется случайным событием 2

Закономерности случайных событий изучает специальный раздел математики, который называется теорией вероятностей 3

Вероятность 1. Изменяющаяся от 0 до 1 мера убеждения в верности гипотезы 2. Предел относительной частоты появления события в последовательности N случайных проб, где N стремится к бесконечности, т. е предел, выраженный как Число появлений данного события N

Относительной частотой случайного события в серии испытаний называется отношение числа испытаний, в которых это событие наступило, к числу всех испытаний 5

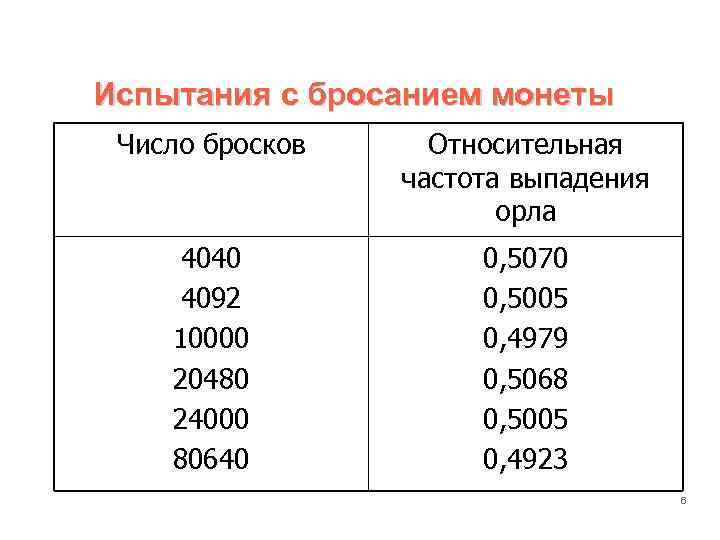Испытания с бросанием монеты Число бросков Относительная частота выпадения орла 4040 4092 10000 20480 24000 80640 0, 5070 0, 5005 0, 4979 0, 5068 0, 5005 0, 4923 6

Результаты наблюдений и опытов показывают, что при большом числе испытаний, проводимых в одних и тех же условиях, относительная частота принимает достаточно устойчивое значение и принимается за вероятность случайного события Такое определение называют статистическим определением вероятности 7

Вероятностью события называется отношение числа благоприятных для него исходов испытания к числу всех равновозможных исходов. Это классическое определение вероятности. 8

• Событие, которое никогда не может произойти, сколько бы раз ни повторялось испытание, называется невозможным событием. • Вероятность невозможного события равна 0. 9

• Событие, которое происходит всегда, сколько бы раз ни повторялось испытание, называется достоверным событием. • Вероятность достоверного события равна 1 10

В саду было совершенно тихо. Замёрзшая земля, покрытая пушистым слоем снега, совершенно смолкла, не отдавая звуков. Зато воздух стал как-то особенно чуток, отчётливо и полно перенося на далёкие расстояния крик вороны, удар топора, легкий треск обломавшейся ветки. Найдем относительную частоту появления буквы О. Всего букв - 217. Буква О – 29. Относительная частота - 11

Многократная проверка показала, что всхожесть семян огурцов определенного сорта равна 0, 9. Посадили 85 семян этого сорта. Найдите ожидаемое число проросших семян. Р = 0, 9 n = 85 m = 0, 9 * 85 = 76, 5 77 (семян) 12

Какова вероятность того, что при бросании игрального кубика выпадет: а) одно очко; б) более 3 очков? а) Р= б) больше трех баллов, т. е. 4, 5, 6. значит Р= 13

Вероятность – количественная мера объективной возможности появления события при реализации определенного комплекса условий. Вероятность события А обозначается как р(А) и выражается в долях единицы или в процентах. Мера вероятности – диапазон ее числовых значений: от 0 до 1 или от 0 до 100%.

Случайное событие – событие, которое при реализации определенного комплекса условий может произойти или не произойти. Его вероятность будет находиться в пределах 0< p(A) < 1 или 0< p(A) < 100%.

Достоверное событие - событие, которое при реализации определенного комплекса условий произойдет непременно. Его вероятность будет равна 1 или 100%.

Невозможное событие - событие, которое при реализации определенного комплекса условий не произойдет никогда. Его вероятность будет равна 0.

В медицинских исследованиях достаточной считается вероятность появления события не менее 0, 95 или 95%. При изучении заболеваний или ситуаций, имеющих важнейшие медико-социальные последствия или высокие показатели летальности и инвалидности, а также при фармакологических исследованиях вероятность появления события должна быть не менее 0, 99 (99%).

Частота появления события (статистическая вероятность) – это отношение числа случаев, в которых реализовался определенный комплекс условий (m), к общему числу случаев (n): p(A)=m/n. Вероятность отсутствия события: q= 1 - p. Например, если вероятность того, что больной останется жив спустя пять лет после операции равна 0. 8 (80%), то вероятность того, что он за этот временной промежуток умрёт равна 0. 2 (20%).

Шанс – это отношение вероятности того, что события произойдёт к вероятности того, что событие не произойдёт. В нашем примере шанс равен 4, так как 0. 8/0. 2=4 Таким образом, вероятность выздоровления в 4 раза больше вероятности смерти. Интерпретация: 1) Если Шанс =1, то вероятность наступления события равна вероятности того, что событие не произойдёт; 2) если Шанс >1, то вероятность наступления события больше вероятности того, что событие не произойдёт; 3) если Шанс <1, то вероятность наступления события меньше вероятности того, что событие не

Правило сложения вероятностей Если два события , А и В, взаимоисключающие, несовместимые, то вероятность события А или В равна сумме их вероятностей: Р(А или В) = р(А) + р(В)

• Например: Вероятность того, что у взрослого человека все зубы сохранены – 0, 67; Вероятность отсутствия некоторых зубов – 0, 24; Вероятность того, что он – беззубый – 0, 09. Какова вероятность того, что у взрослого человека есть хотя бы несколько зубов?

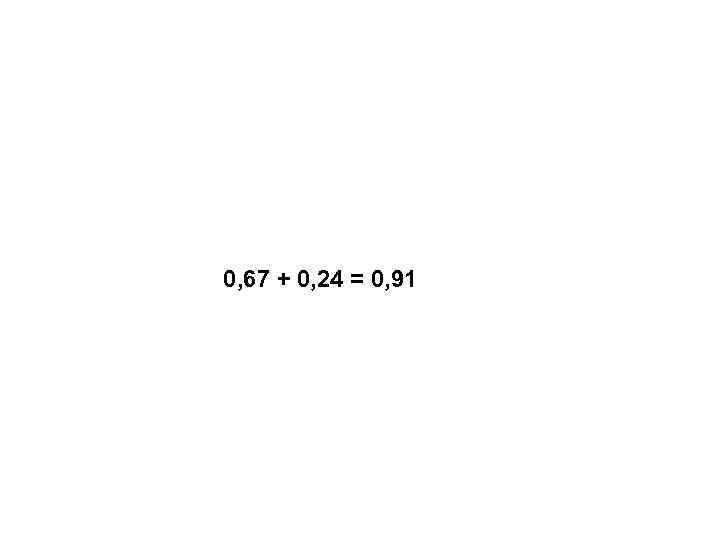0, 67 + 0, 24 = 0, 91

Правило умножения вероятностей: Если два события, А и В, независимы (т. е. возникновение одного события не влияет на возможность появления другого), то вероятность того, что оба события произойдут, равна произведению вероятности каждого: Р(А и В) = р(А) × р(В)

Например: Какова вероятность того, что у 2 -х не имеющих отношения друг к другу больных, ожидающих приема к стоматологу, есть все зубы?

0, 67 × 0, 67 = 0, 45

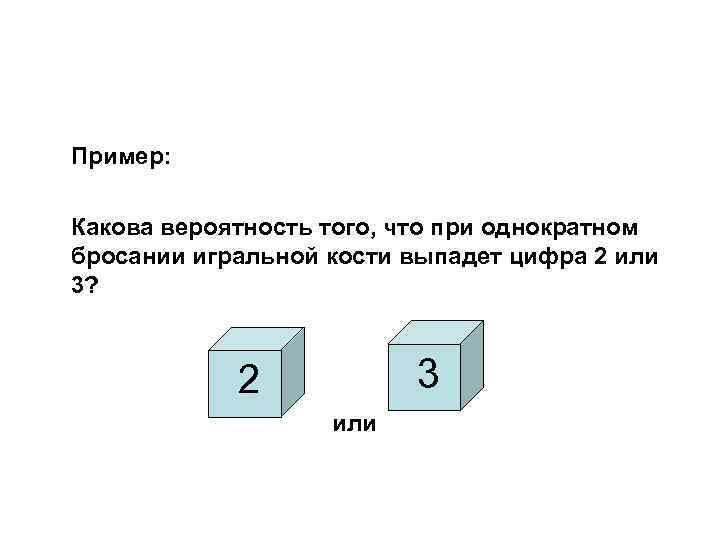Пример: Какова вероятность того, что при однократном бросании игральной кости выпадет цифра 2 или 3? 3 2 или

р(2) + р(3) = 1/6 + 1/6 = 1/3 (формула сложения для несовместных событий)

Пример: Какова вероятность того, что при двукратном бросании игральной кости оба раза выпадет цифра 6? 6 6

1 -е бросание: р(6) = 1/6 2 -е бросание: р(6) = 1/6 р(6) × р(6) = 1/ 6 × 1/6 = 1/36 (формула умножения для независимых событий)

Случайная величина – величина, которая при реализации определенного комплекса условий может принимать различные значения.

Закон больших чисел: при достаточно большом числе наблюдений случайные отклонения взаимно погашаются и проявляется основная тенденция (закономерность).

ВНИМАНИЕ ! От вида распределения зависит выбор статистического пути описания (обобщения) и анализа количественного признака

Вид распределения Под видом распределения случайной величины понимают соответствие, устанавливаемое между всеми возможными числовыми значениями случайной величины и вероятностями их появления в совокупности.

Вид распределения Вид (закон) распределения может быть представлен: - аналитической зависимостью в виде формулы; - в виде графического изображения; - в виде таблицы

Виды распределения - нормальное - биноминальное (Бернулли) - распределение Пуассона - t- распределение Стьюдента - распределение Пирсона (Хи-квадрат) - F-распределение (Фишера) - логнормальное

Нормальное распределение (гауссово, симметричное, колообразное) (normal, Gaussian distribution) – описывает совместное воздействие на изучаемое явление небольшого числа случайно сочетающихся факторов (по сравнению с общей суммой факторов), число которых неограничено велико. Встречается в природе наиболее часто, за что и получило название «нормального» . Характеризует распределение непрерывных случайных величин.

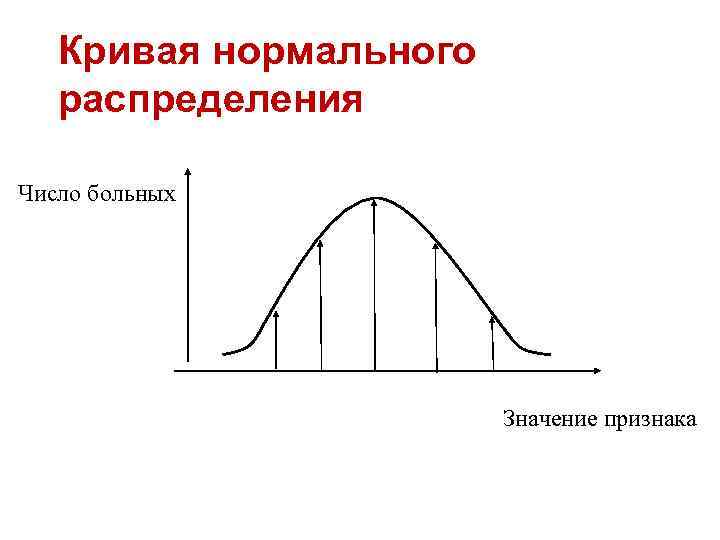Кривая нормального распределения Число больных Значение признака

• Биномиальное (Бернулли) распределение (binomial, Bernoulli distribution) – описывает распределение частоты события, обладающего постоянной вероятностью появления при многократных испытаниях. • При большом числе испытаний стремиться к нормальному.

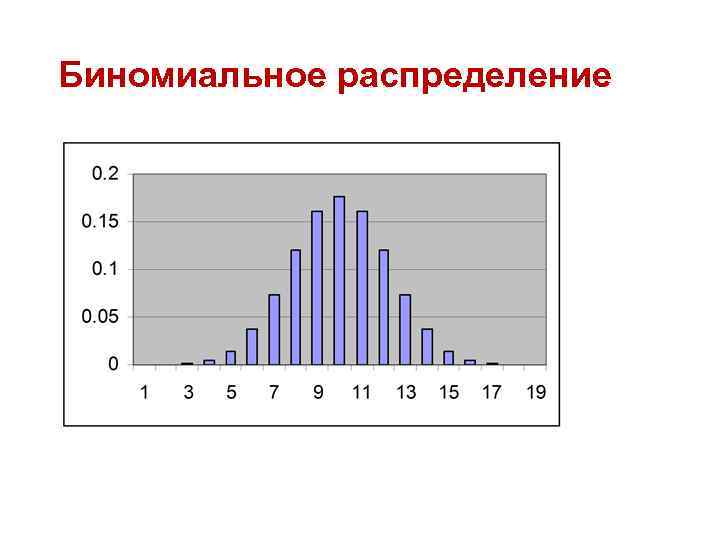Биномиальное распределение

• Крайним вариантом биномиального распределения является альтернативное распределение, при котором вся совокупность распределяется на две части (две альтернативы). • Биномиальное распределение характеризует распределение дискретных случайных величин.

• Распределение Пуассона – описывает события, при которых с возрастанием значения случайной величины, вероятность появления ее в совокупности резко уменьшается. • Распределение Пуассона характерно для редких событий и может рассматриваться также как крайний вариант биномиального. Характеризует распределение дискретных случайных величин.

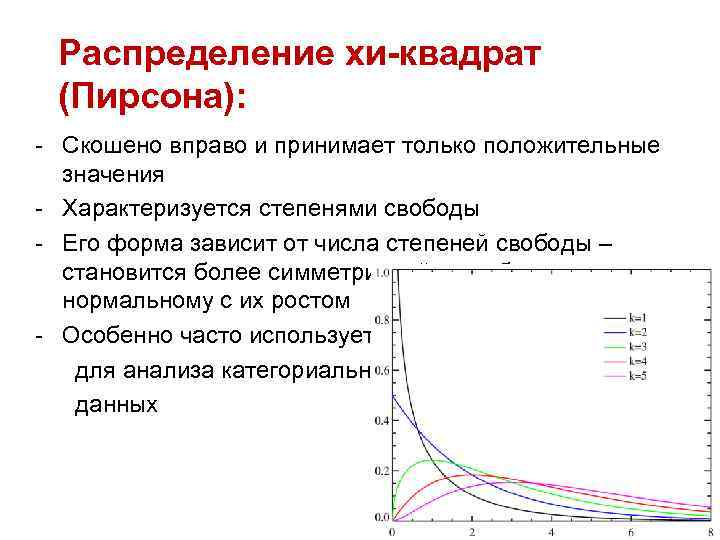Распределение хи-квадрат (Пирсона): - Скошено вправо и принимает только положительные значения - Характеризуется степенями свободы - Его форма зависит от числа степеней свободы – становится более симметричной и приближается к нормальному с их ростом - Особенно часто используется для анализа категориальных данных

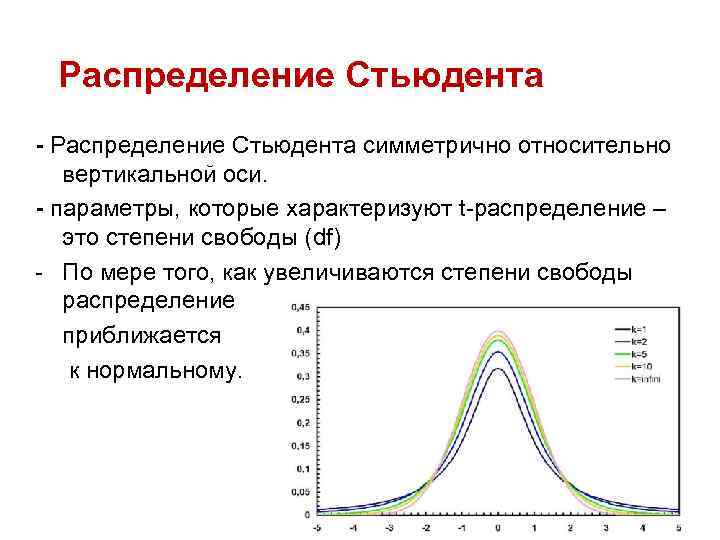Распределение Стьюдента - Распределение Стьюдента симметрично относительно вертикальной оси. - параметры, которые характеризуют t-распределение – это степени свободы (df) - По мере того, как увеличиваются степени свободы распределение приближается к нормальному.

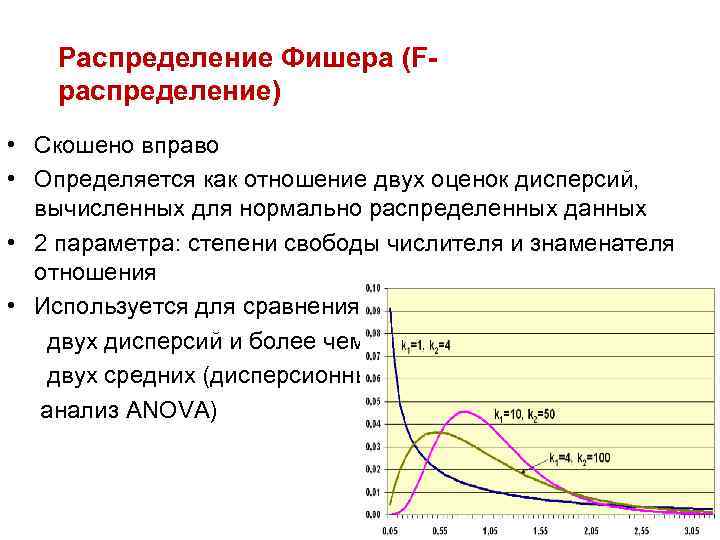Распределение Фишера (Fраспределение) • Скошено вправо • Определяется как отношение двух оценок дисперсий, вычисленных для нормально распределенных данных • 2 параметра: степени свободы числителя и знаменателя отношения • Используется для сравнения двух дисперсий и более чем двух средних (дисперсионный анализ ANOVA)

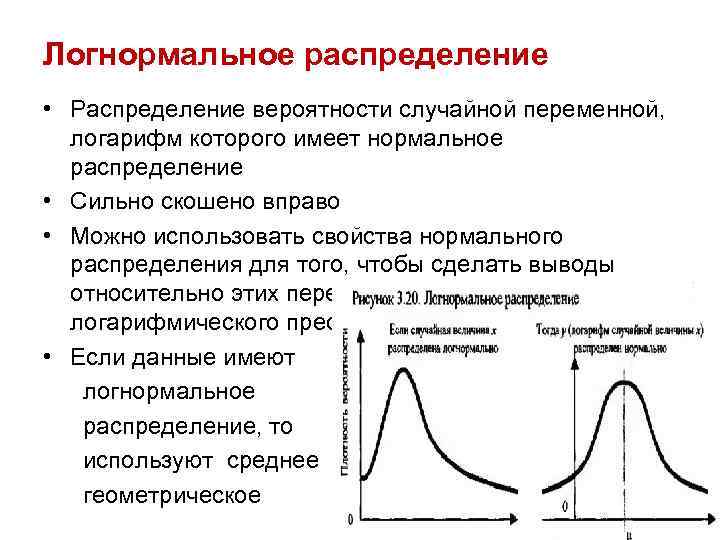Логнормальное распределение • Распределение вероятности случайной переменной, логарифм которого имеет нормальное распределение • Сильно скошено вправо • Можно использовать свойства нормального распределения для того, чтобы сделать выводы относительно этих переменных после логарифмического преобразования данных • Если данные имеют логнормальное распределение, то используют среднее геометрическое

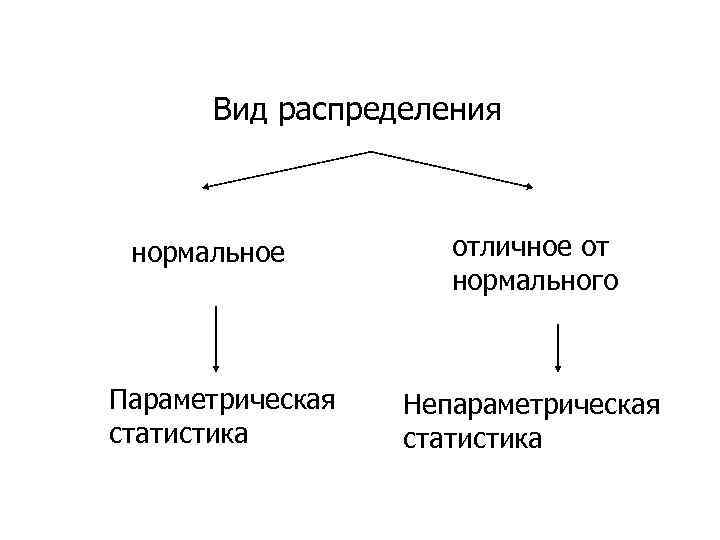Вид распределения нормальное Параметрическая статистика отличное от нормального Непараметрическая статистика

Непараметрические методы: • не требуют предварительного знания вида распределения; • не требуют предварительного расчета параметров распределения (средних величин, стандартного отклонения и др. ); • позволяют сравнивать совокупности с номинальными и порядковыми признаками; • просты в применении.

Отрицательные стороны непараметрических методов: • обладают меньшей мощностью, чем параметрические; • имеют существенные ограничения в применении по числу наблюдений

Проверка нормальности распределения По соотношению средней арифметической, моды и медианы: • при нормальном распределении, которое обладает симметричностью: • правило "двух третей" Юла:

Проверка нормальности распределения • если распределение симметрично: Me = Mo • если распределение обладает правосторонней асимметрией: Me > Mo • если распределение имеет левостороннюю асимметрию: Me < Mo

Проверка нормальности распределения По коэффициенту асимметрии (skewness): • если распределение симметрично: =0 • при правосторонней асимметрии: >0 • при левосторонней асимметрии: <0

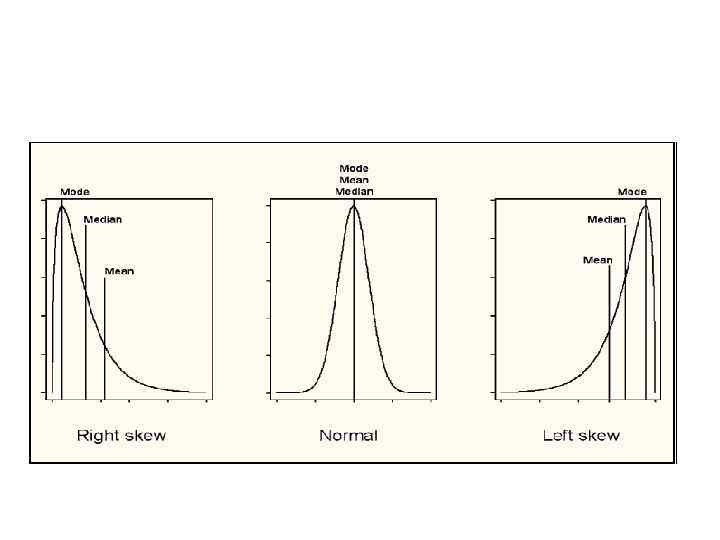
Проверка нормальности распределения Kurtosis (Коэффициент эксцесса): • Коэффициент указывает, является ли распределение пологим (при большом значении коэффициента) или островершинным. Коэффициент вариации равен нулю, если наблюдения подчиняются нормальному распределению. • Если коэффициент вариации значительно отличается от нуля, то гипотезу о том, что данные взяты из нормально распределенной генеральной совокупности, следует отвергнуть.

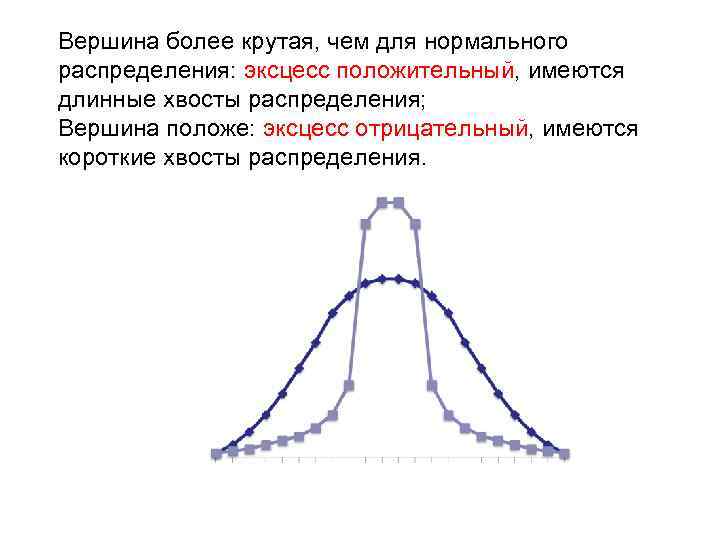Вершина более крутая, чем для нормального распределения: эксцесс положительный, имеются длинные хвосты распределения; Вершина положе: эксцесс отрицательный, имеются короткие хвосты распределения.

Проверка нормальности распределения • Если Ме занимает срединное положение между 25 -м и 75 -м процентилем, то распределение близко к нормальному.

Проверка нормальности распределения Тесты на нормальность: • Шапиро-Вилка (Shapiro-Wilk) • Колмогорова-Смирнова (Kolmogorov. Smirnov) • Крамера-вон Майса (Kramer-von Mises) • Андерсона-Дарлинга (Anderson. Darling)

Способы "нормализующего преобразования" (transformation to normality) данных : - гармоническое преобразование: 1 /х; - извлечение квадратного корня; - логарифмирование (дает наиболее точное приближение): log xi

• Успешность преобразования данных оценивают по коэффициенту асимметрии: чем ближе он к 0, тем ближе экспериментальное распределение к нормальному.

Логарифм • Логари фм числа b по основанию a определяется как показатель степени, в которую надо возвести основание a, чтобы получить число b. • Обозначение: logab, произносится: "логарифм b по основанию a". х= logab равносильно решению уравнения ax =b. Например, log 28=3, потому что 23=8 • Нахождение • Вычисление логарифма называется логарифмированием.

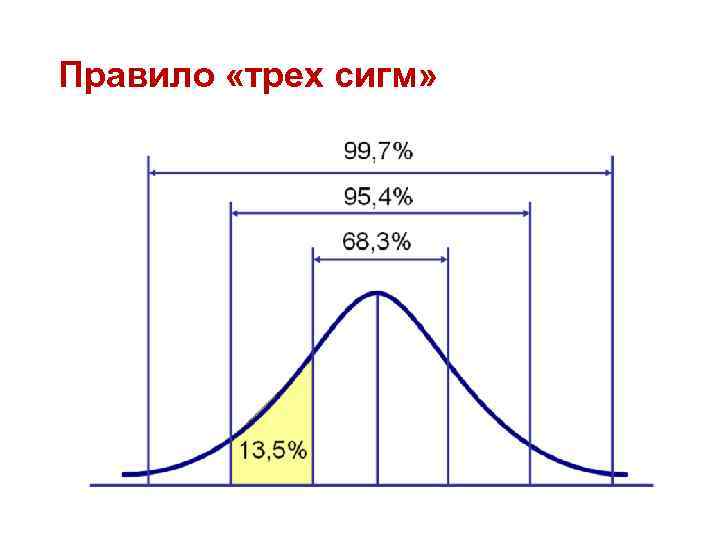Правило «трех сигм»

Следствия 1. Площадь под кривой нормального распределения на интервале от μ - σ до μ + σ составляет 68, 27% всей площади. На этом интервале сосредоточено 68, 27% всех значений случайной величины. 2. Площадь под кривой нормального распределения на интервале от μ - 2σ до μ + 2σ составляет 95, 45% всей площади. На этом интервале сосредоточено 95, 45% всех значений случайной величины. 3. Площадь под кривой нормального распределения на интервале от μ - 3σ до μ + 3σ составляет 99, 73% всей площади. На этом интервале сосредоточено 99, 73% всех значений случайной величины.

Следствия Площадь 90% площади 95% площади 99% площади Интервал μ ± 1, 64 σ μ ± 1, 96 σ μ ± 2, 50 σ

Пример Батарейки работают в среднем 19 часов со стандартным отклонением 1, 2 часа. Можно утверждать, что 95, 45% батареек служат от 16, 6 до 21, 4 часа.

Центральная предельная теорема Для бесконечного числа независимых случайных выборок одинакового объема, извлеченных из генеральной совокупности, выборочное распределение любой линейной комбинации выборочных средних будет стремиться к нормальному при объеме выборки, стремящейся к бесконечности.