Verilog-A is for Equation Specification not for Modeling

Verilog-A is for Equation Specification, not for Modeling Colin Mc. Andrew Laurent Lemaitre Zoltan Huszka Geoffrey Coram Freescale Semiconductor Austriamicrosystems Analog Devices MOS-AK Meeting Saturday December 13, 2008

Overview • A Brief History of Verilog-A for Compact Modeling • A Brief Review of How Circuit Simulators Work • How to Leverage Understanding of How Simulators Work to Implement Desired Equations § thinking outside the “equivalent network” modeling box § example 1: BJT excess phase § example 2: single formulation resistor that can handle R=0 • Summary Mc. Andrew/Lemaitre/Huszka/Coram MOS-AK December 2008 2

What is Verilog-A? • Initially (mid to late 1990’s), a language for analog behavioral modeling to enable § top down AMS design at the block level § efficient top-level AMS verification • VHDL-AMS is a “competing” language developed around the same time for the same purposes • So how does Verilog-A relate to compact modeling? Mc. Andrew/Lemaitre/Huszka/Coram MOS-AK December 2008 3

Automation in Compact Modeling • In the late 1980’s automation began to creep into the development of simulators § especially for the time-consuming and error-prone task of implementing compact models (symbolic derivative generation) § added impetus to the on-going migration from “diffused” model code to “modular” model code • Simulator-model interfaces of the 1980’s and 1990’s: § WATAND § Saber/MAST – major commercial success § Tektronix (very early pioneer) § ADMIT plus various compilers (AT&T) § i. SMILE § CMC Type-II interface (DOA circa 1995; engineering ≠ CS) Mc. Andrew/Lemaitre/Huszka/Coram MOS-AK December 2008 4

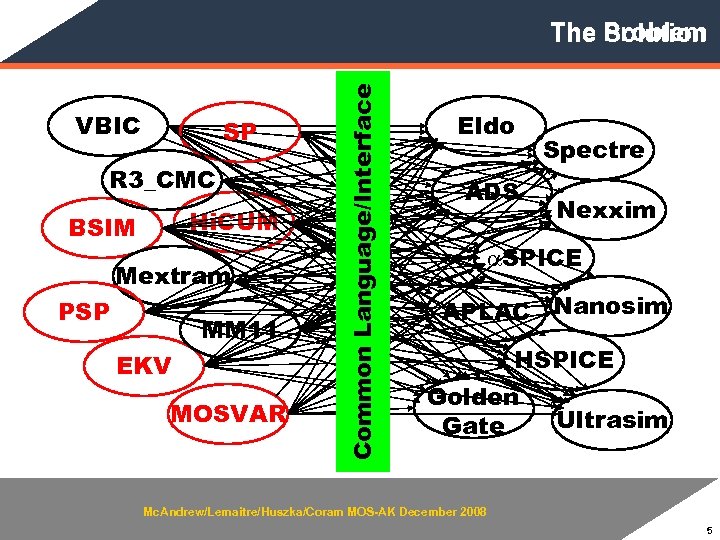VBIC SP R 3_CMC Hi. CUM BSIM Mextram PSP MM 11 EKV MOSVAR Common Language/Interface The Problem Solution Eldo ADS Spectre Nexxim a. SPICE APLAC Nanosim HSPICE Golden Gate Ultrasim Mc. Andrew/Lemaitre/Huszka/Coram MOS-AK December 2008 5

Automated Model Implementation • Mostly flopped in mid 1990’s § VBIC was the first public model defined in high level code § generated FORTRAN and C also provided > these were used > high-level pseudo-code was not! (except by Tektronix) > chasm between engineers and advanced software techniques • Many misconceptions § code is slow compared to hand-coded C > within 10% of hand coded and getting better > will be faster one day (proven already), then works for all models! § cannot use for parameter extraction > if it’s in a simulator it’s in your simulator-based extractor! § different code for different simulators will give different results > different compile flags on the same platform give different results! Mc. Andrew/Lemaitre/Huszka/Coram MOS-AK December 2008 6

Enter Verilog-A • Significant issue with the concept (high-level language + compilers) was the lack of a standard high-level language! • Verilog-A was obviously the solution for this § VHDL-AMS touted as well initially • Minor deficiencies overcome by compact model additions • defined in LRM 2. 2 CMC accepted models defined in Verilog-A circa 2004 • Verilog-A has become the de facto standard language for defining compact models Mc. Andrew/Lemaitre/Huszka/Coram MOS-AK December 2008 7

Moving Beyond “Models” • You can use Verilog-A to define “physical” compact models • But this can be very restrictive § constrained to think in terms of equivalent networks § constrained to think in terms of I(V), Q(V) relations • A circuit simulator is an equation solver • Think of what equations you want to force the simulator to solve, then develop Verilog-A constructs to force this § not thinking in terms of physical representation Mc. Andrew/Lemaitre/Huszka/Coram MOS-AK December 2008 8

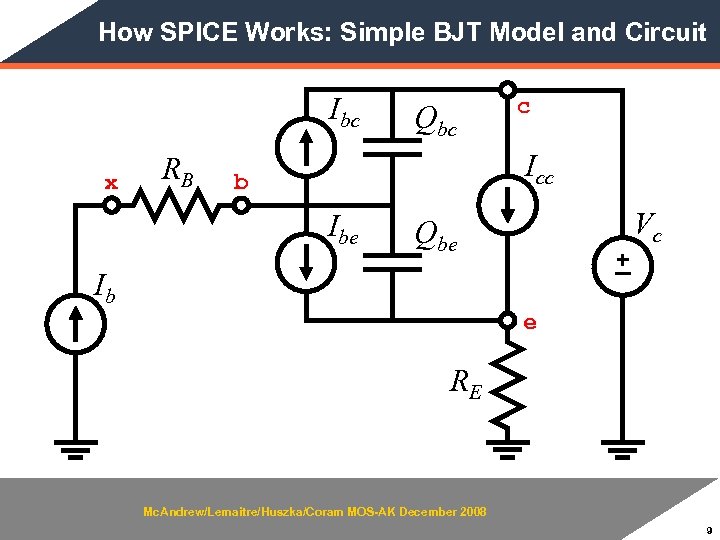How SPICE Works: Simple BJT Model and Circuit Ibc x RB Qbc c Icc b Ibe Vc Qbe + – Ib e RE Mc. Andrew/Lemaitre/Huszka/Coram MOS-AK December 2008 9

System Equations (DC): MNA • Unknowns are V(x), V(b), V(c), V(e), and Ic=I(Vc) x b e c • Vbe=V(b)–V(e) and Vbc=V(b) –V(c) Mc. Andrew/Lemaitre/Huszka/Coram MOS-AK December 2008 10

Branch Jacobian Entry (Element Matrix Stamp) • Solve KCL SI (V)=f(V)=0 at each node, plus the “voltage equation” for voltage sources (and inductors) § nonlinear, so need iterative Newton solution § Vk+1=Vk+d. Vk, Jkd. Vk=-f(Vk), Jk= ∂I/∂V |V=Vk • Easy to set up Jacobian Jk in an algorithmic fashion § rows are defined by nodes that the current flows between > +ve for flow into node, –ve for flow out-of node § columns are defined by the branch control voltages > +ve for first node, –ve for second, for Vab=V (a)-V (b) § voltage sources and inductors add a row for the voltage equation and a column (unknown system variable) for the current Mc. Andrew/Lemaitre/Huszka/Coram MOS-AK December 2008 11

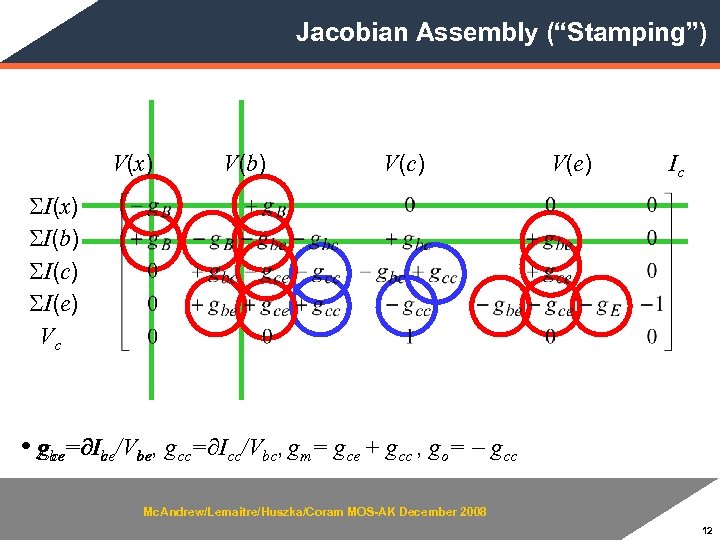Jacobian Assembly (“Stamping”) V(x) V(b) V(c) V(e) Ic SI(x) SI(b) SI(c) SI(e) Vc • gbe=∂Ibe/Vbe, gcc=∂Icc/Vbc, gm= gce + gcc , go= - gcc ce cc Mc. Andrew/Lemaitre/Huszka/Coram MOS-AK December 2008 12

SPICE • Circuit simulators are not really “circuit simulators” § for DC they are multidimensional nonlinear equation solvers § for transient they are nonlinear ordinary differential equation (ODE) solvers > multidimensional nonlinear equation solvers at each time point • Instead of thinking of Verilog-A as a means to define equivalent network models, think of it as a means of specifying equations for numerical solution § formulate the equations you want § understand how MNA equations are set up § work out how to use Verilog-A to set up the desired equations Mc. Andrew/Lemaitre/Huszka/Coram MOS-AK December 2008 13

Weil-Mc. Namee Excess Phase for BJTs • Goal: implement a phase shift for gm with the least possible change in the magnitude of gm § network approach leads to 2 nd order Bessel (linear phase) filter § straight forward to implement as RLC circuit (L. Wagner, IBM) Itxf =V(xf 2) TD /3 xf 1 Itzf TD xf 2 1 W Mc. Andrew/Lemaitre/Huszka/Coram MOS-AK December 2008 14

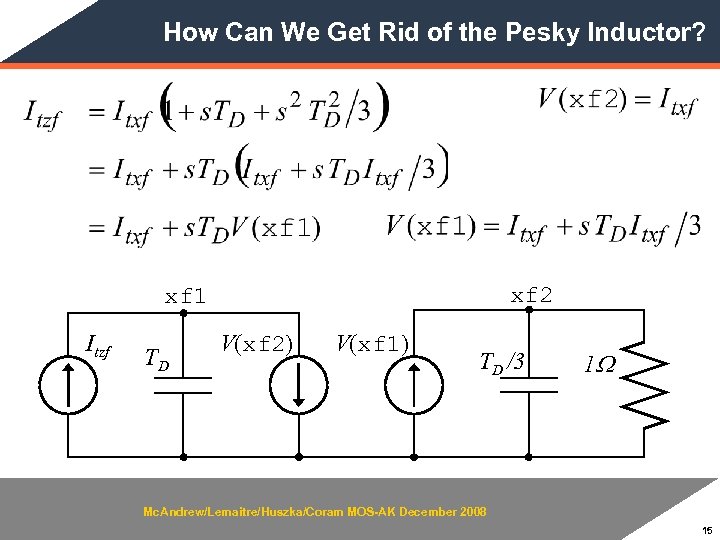How Can We Get Rid of the Pesky Inductor? xf 2 xf 1 Itzf TD V(xf 2) V(xf 1) TD /3 1 W Mc. Andrew/Lemaitre/Huszka/Coram MOS-AK December 2008 15

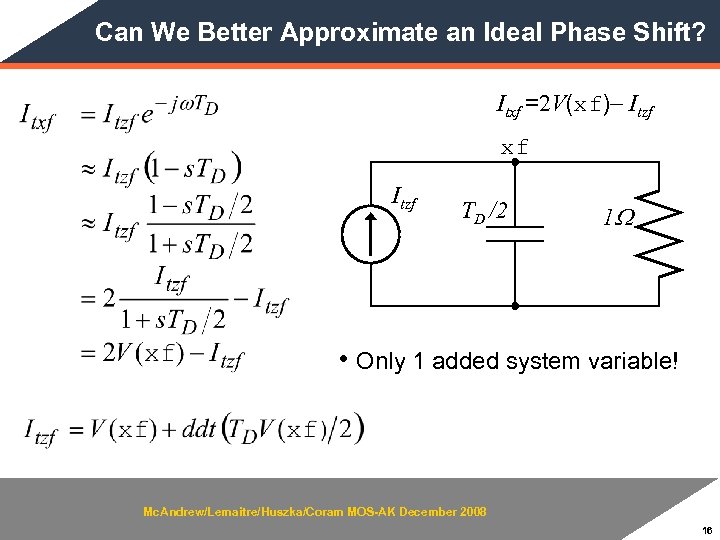Can We Better Approximate an Ideal Phase Shift? Itxf =2 V(xf)- Itzf xf Itzf TD /2 1 W • Only 1 added system variable! Mc. Andrew/Lemaitre/Huszka/Coram MOS-AK December 2008 16

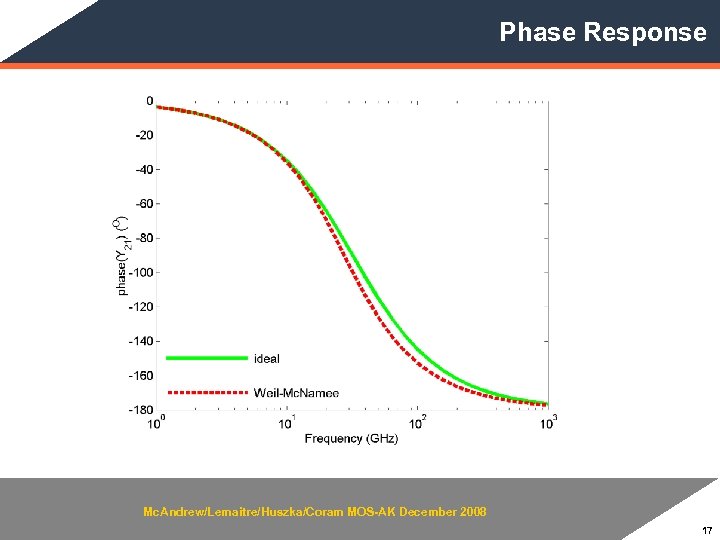Phase Response Mc. Andrew/Lemaitre/Huszka/Coram MOS-AK December 2008 17

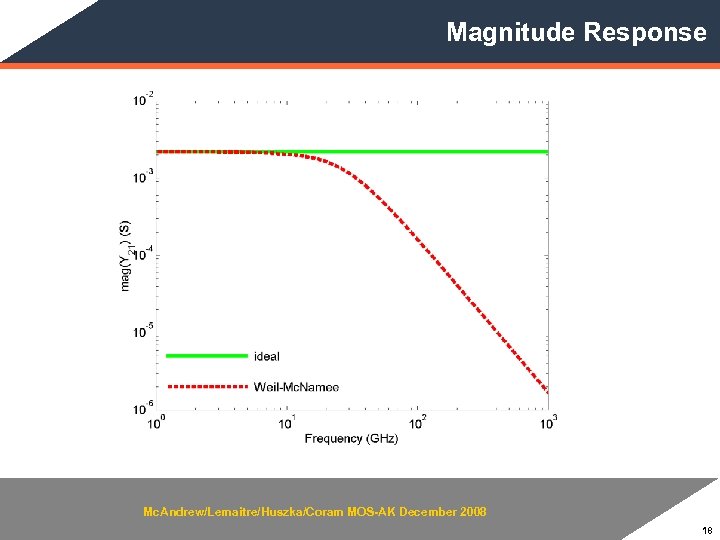Magnitude Response Mc. Andrew/Lemaitre/Huszka/Coram MOS-AK December 2008 18

What about Resistors? p m Mc. Andrew/Lemaitre/Huszka/Coram MOS-AK December 2008 19

The “Solution”. . . sort of • For “reasonable” R: § natural for NA (SPICE) § efficient for NA § nasty for R=0 or small R • For “small” R: § extra MNA system variable § no worries for R=0 or small R Mc. Andrew/Lemaitre/Huszka/Coram MOS-AK December 2008 20

The “. . . sort of” Solution `include "disciplines. h" `define rm 0. 001 module r_va(p, m); inout p, m; electrical p, m; parameter real R = 1. 0 from[0. 0: inf); analog begin : analog. Block if (R<`rm) V(p, m) <+ I(p, m)*R; EASY TO DEFINE else I(p, m) <+ V(p, m)/R; HARD TO IMPLEMENT end // analog. Block endmodule Mc. Andrew/Lemaitre/Huszka/Coram MOS-AK December 2008 21

Why “. . . sort of” is not Enough • Does work in Verilog-A § excellent feature of the language • Does not (easily) work for § built-in model implementation via ADMS § some model interfaces for some simulators § dynamic switching for the case when R varies with bias • Do not want to switch formulations during iterative solution § dynamically adds extra system variable I(p, m) • Observation: must have this current for V=RI formulation • Conclusion: explicitly include in model formulation Mc. Andrew/Lemaitre/Huszka/Coram MOS-AK December 2008 22

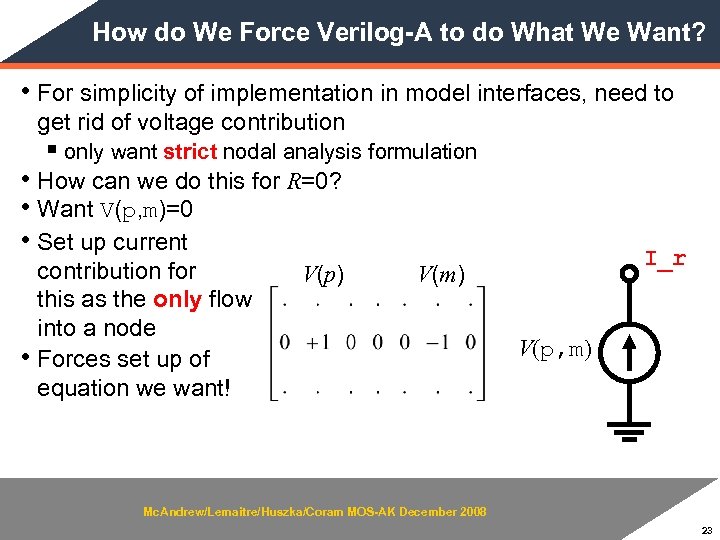How do We Force Verilog-A to do What We Want? • For simplicity of implementation in model interfaces, need to get rid of voltage contribution § only want strict nodal analysis formulation • How can we do this for R=0? • Want V(p, m)=0 • Set up current • contribution for this as the only flow into a node Forces set up of equation we want! V(p) I_r V(m) V(p, m) Mc. Andrew/Lemaitre/Huszka/Coram MOS-AK December 2008 23

The R=0 Solution `include "disciplines. h" module r_va(p, m); inout p, m; electrical p, m, I_r; parameter real R = 1. 0 from[0. 0: inf); analog begin : analog. Block I(I_r) <+ V(p, m); I(p, m) <+ 1. 0 e-6*V(I_r); end // analog. Block endmodule second equation forces V(I_r) to be current flowing between p and m Mc. Andrew/Lemaitre/Huszka/Coram MOS-AK December 2008 24

Extension for Small Nonzero R `include "disciplines. h" module r_va(p, m); inout p, m; electrical p, m, I_r; parameter real R = 1. 0 from[0. 0: inf); analog begin : analog. Block I(I_r) <+ V(p, m)-1. 0 e-6*R*V(I_r); I(p, m) <+ 1. 0 e-6*V(I_r); end // analog. Block endmodule first equation forces V(p, m)=I*R (voltage on node I_r is current p→m) Mc. Andrew/Lemaitre/Huszka/Coram MOS-AK December 2008 25

Final Result `include "disciplines. h" `define rm 0. 001 module r_va(p, m); inout p, m; electrical p, m, I_r; parameter real R = 1. 0 from[0. 0: inf); analog begin : analog. Block I(I_r) <+ V(p, m)-1. 0 e-6*R*V(I_r); if (R<`rm) I(p, m) <+ 1. 0 e-6*V(I_r); else I(p, m) <+ V(p, m)/R; // I=G*V formulation end // analog. Block endmodule Mc. Andrew/Lemaitre/Huszka/Coram MOS-AK December 2008 26

Final Model • Manipulated Verilog-A equations we want to solve • Resistor model that does not switch formulations from current contribution to voltage contribution § strictly nodal formulation § easy to implement in all simulator model interfaces § numerically well behaved for all R≥ 0 § can be adapted to use same “switch” for voltage variable R > direct bias dependence > indirect bias dependence (e. g. self-heating) • Cost is added system variable V(I_r) is added for all values of R, not just R<`rm Mc. Andrew/Lemaitre/Huszka/Coram MOS-AK December 2008 27

Summary • Circuit simulators are equation, not circuit, solvers • Historical modeling approach of equivalent networks and a physical approach may not always give desired result • By thinking about what equations you want to implement or solve, and understanding how MNA is set up, you can use Verilog-A to implement “non-obvious” but useful models • Note: if “currents” are mapped to node voltages (i. e. system variables), they need to be scaled by the voltage/current tolerance ratio (default is 1. 0 e 6) Mc. Andrew/Lemaitre/Huszka/Coram MOS-AK December 2008 28