Verification of Parameterized Hierarchical State Machines Using Action

Verification of Parameterized Hierarchical State Machines Using Action Language Verifier Tuba Yavuz-Kahveci University of Florida, Gainesville Tevfik Bultan University of California, Santa Barbara download Action Language Verifier at: //www. cs. ucsb. edu/~bultan/composite/

Outline • • An Example: Airport Ground Traffic Control Hierarchical State Machines Action Language Verifier Composite Symbolic Library Infinite State Verification Parameterized Verification Experimental Results Related work

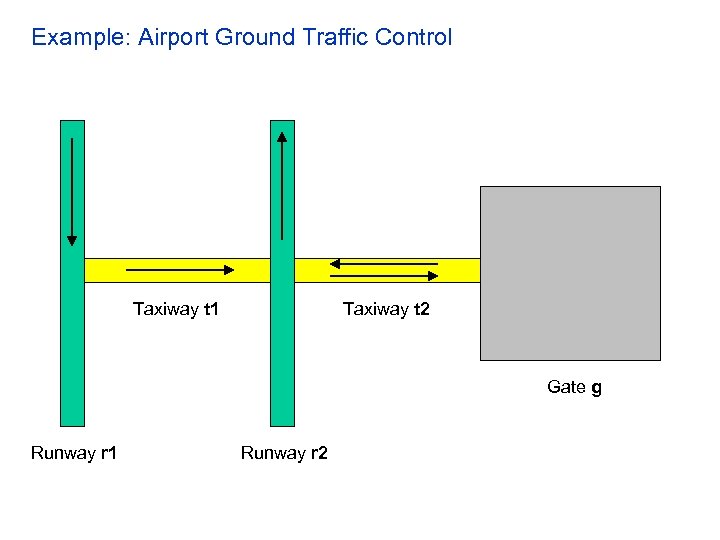Example: Airport Ground Traffic Control Taxiway t 1 Taxiway t 2 Gate g Runway r 1 Runway r 2

Control Logic • An arriving airplane lands using runway r 1, navigates to taxiway t 1, crosses runway r 2, navigates to taxiway t 2 and parks at gate g • A departing airplane starts at gate g, navigates to taxiway t 2, and takes off using runway r 2 • Only one airplane can use a runway at any given time • Only one airplane can use a taxiway at any given time • An airplane taxiing on taxiway t 1 can cross runway r 2 only if no airplane is taking off at the moment

Hierarchical State Machines In a Hierarchical State Machine (HSM) [Harel 87] • States can be combined to form superstates • OR decomposition of a superstate – The system can be in only one of the substates at any given time • AND decomposition of a superstate – The system has to be in all of the substates at the same time • Transitions – Transitions between states are labeled as trigger-event [ guard-condition ] / generated-event

Airport Ground Traffic Control Airplane[*] t 1 r 1 empty land[in(r 1. empty)]/taxii 1 E flow fly landing land/ taxii 1 E[in(t 1. empty)] /taxii 2 E takingoff taxiing 1 r 2 empty occupied taxii 1 E [in(t 1. empty)] /taxii 2 E occupied t 2 g empty parking empty occupied taxiing 2

Parameterized Hierarchical State Machines • We use “*” to denote arbitrary number of instantiations of a state – These instantiations are asynchronously composed using interleaving semantics • We used Action Language Verifier to verify CTL properties parameterized hierarchical state machines • In order to verify a specification for arbitrary instances of a module we used counting abstraction technique

Action Language [Bultan, ICSE 00], [Bultan, Yavuz-Kahveci, ASE 01] • A state based language – Actions correspond to state changes • States correspond to valuations of variables – boolean – enumerated – integer (possibly unbounded) – there is an extension to heap variables (i. e. , pointers) but this is not included in the current version • Parameterized constants – specifications are verified for every possible value of the constant

Action Language • Transition relation is defined using actions – Atomic actions: Predicates on current and next state variables – Action composition: • asynchronous (|) or synchronous (&) • Modular – Modules can have submodules – A modules is defined as asynchronous and/or synchronous compositions of its actions and submodules

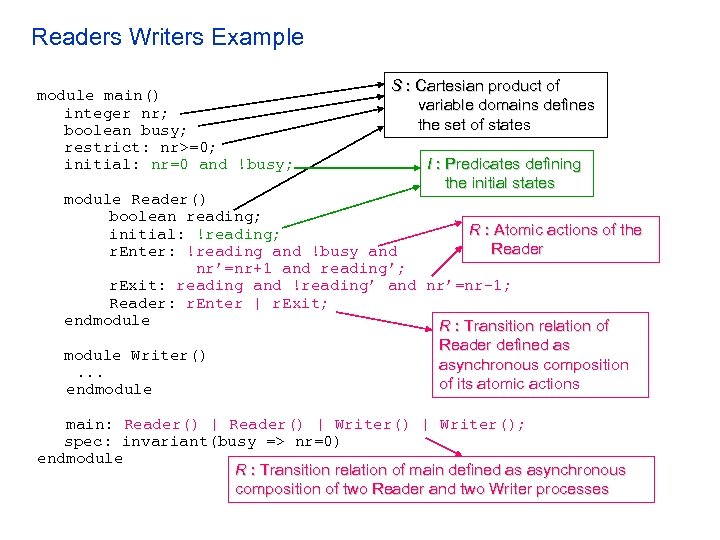Readers Writers Example module main() integer nr; boolean busy; restrict: nr>=0; initial: nr=0 and !busy; S : Cartesian product of variable domains defines the set of states I : Predicates defining the initial states module Reader() boolean reading; R : Atomic actions of the initial: !reading; Reader r. Enter: !reading and !busy and nr’=nr+1 and reading’; r. Exit: reading and !reading’ and nr’=nr-1; Reader: r. Enter | r. Exit; endmodule R : Transition relation of Reader defined as module Writer() asynchronous composition. . . of its atomic actions endmodule main: Reader() | Writer(); spec: invariant(busy => nr=0) endmodule R : Transition relation of main defined as asynchronous composition of two Reader and two Writer processes

Translating HSMs to Action Language • Transitions (arcs) correspond to actions • OR states correspond to enumerated variables and they define the state space • Transitions (actions) of OR states are combined using asynchronous composition • Transitions (actions) of AND states are combined using synchronous composition

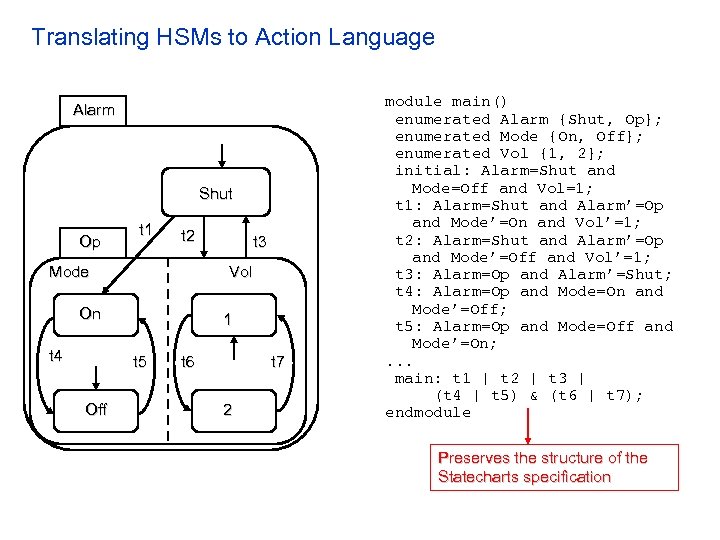Translating HSMs to Action Language Alarm Shut Op t 1 t 2 Mode Vol On t 4 1 t 5 Off t 3 t 6 t 7 2 module main() enumerated Alarm {Shut, Op}; enumerated Mode {On, Off}; enumerated Vol {1, 2}; initial: Alarm=Shut and Mode=Off and Vol=1; t 1: Alarm=Shut and Alarm’=Op and Mode’=On and Vol’=1; t 2: Alarm=Shut and Alarm’=Op and Mode’=Off and Vol’=1; t 3: Alarm=Op and Alarm’=Shut; t 4: Alarm=Op and Mode=On and Mode’=Off; t 5: Alarm=Op and Mode=Off and Mode’=On; . . . main: t 1 | t 2 | t 3 | (t 4 | t 5) & (t 6 | t 7); endmodule Preserves the structure of the Statecharts specification

Action Language Verifier [Bultan, Yavuz-Kahveci ASE 01], [Yavuz-Kahveci, Bar, Bultan CAV 05] Action Language Specification Action Language Parser Composite Symbolic Library Model Checker Omega Library Counter-example Verified I don’t know Presburger Arithmetic Manipulator CUDD Package BDD Manipulator MONA Automata Manipulator

Temporal Properties Fixpoints [Emerson and Clarke 80] EF( p) states that can reach p p Pre( p)) . . . p • • • EF( p) Initial states initial states that satisfy EF( p) initial states that violate AG(p) EG( p) states that can avoid reaching p p Pre( p)) . . . • • • EG( p) Initial states initial states that satisfy EG( p) initial states that violate AF(p)

Symbolic Model Checking [Mc. Millan et al. LICS 90] • Represent sets of states and the transition relation as Boolean logic formulas • Fixpoint computation becomes formula manipulation – pre and post-condition computations: Existential variable elimination – conjunction (intersection), disjunction (union) and negation (set difference), and equivalence check • Use an efficient data structure – Binary Decision Diagrams (BDDs)

Which Symbolic Representation to Use? BDDs • canonical and efficient representation for Boolean logic formulas • can only encode finite sets x y {(T, T), (T, F), (F, T)} F x a > 0 b = a+1 T y F F Linear Arithmetic Constraints • can encode infinite sets • two representations – polyhedra – automata • not efficient for encoding boolean domains T T {(1, 2), (2, 3), (3, 4), . . . }

Composite Model Checking [Bultan, Gerber, League ISSTA 98, TOSEM 00] • Map each variable type to a symbolic representation – Map boolean and enumerated types to BDD representation – Map integer type to a linear arithmetic constraint representation • Use a disjunctive representation to combine different symbolic representations: composite representation • Each disjunct is a conjunction of formulas represented by different symbolic representations – we call each disjunct a composite atom

Composite Representation composite atom symbolic rep. 1 symbolic rep. 2 symbolic rep. t Example: x: integer, y: boolean x>0 and x´ x-1 and y´ or x<=0 and x´ x and y´ y arithmetic constraint representation BDD

Composite Symbolic Library [Yavuz-Kahveci, Tuncer, Bultan TACAS 01], [Yavuz-Kahveci, Bultan STTT 03] • • Uses a common interface for each symbolic representation Easy to extend with new symbolic representations Enables polymorphic verification Multiple symbolic representations: – As a BDD library we use Colorado University Decision Diagram Package (CUDD) [Somenzi et al] – For integers we use two representations • Polyhedral representation provided by the Omega Library [Pugh et al] • An automata representation we developed using the automata package of MONA [Klarlund et al]

Composite Symbolic Library Class Diagram Symbolic +union() +is. Satisfiable() +is. Subset() +forward. Image() Int. Bool. Sym. Auto Int. Sym. Auto –representation: automaton +union() • • • MONA Int. Sym Comp. Sym –representation: BDD –representation: list of Polyhedra –representation: list of com. Atom +union() + union() • • • Bool. Sym CUDD Library OMEGA Library • • • comp. Atom –atom: *Symbolic

Pre and Post-condition Computation Variables: x: integer, y: boolean Transition relation: R: x>0 and x´ x-1 and y´ or x<=0 and x´ x and y´ y Set of states: s: x=2 and !y or x=0 and !y Compute post(s, R)

Pre and Post-condition Distribute R: x>0 and x´ x-1 and y´ or x<=0 and x´ x and y´ y s: x=2 and !y or x=0 and y post(s, R) = post(x=2 , x>0 and x´ x-1) post(!y , y´) x=1 y post(x=2 , x<=0 and x´ x) post (!y , y´ y) false !y post(x=0 , x>0 and x´ x-1) post(y , y´) false y post (x=0 , x<=0 and x´ x) post (y, y´ y ) x=0 y = x=1 and y or x=0 and y

Polymorphic Verifier Symbolic Tran. Sys: : check(Node f) { • • • Symbolic s = check(f. child); switch f. op { case EX: s. pre(trans. Relation); case EF: do sold = s; s. pre(trans. Relation); s. union(sold); while not sold. is. Equal(s) • • • } } Action Language Verifier is polymorphic It becomes a BDD based model checker when there or no integer variables

Undecidability Conservative Approximations • Compute a lower ( p ) or an upper ( p+ ) approximation to the truth set of the property ( p ) using truncated fixpoints and widening • Action Language Verifier can give three answers: I p 1) “The property is satisfied” states which violate the property I p p 3) “I don’t know” p p+ p 2) “The property is false and here is a counter-example”

Arbitrary Number of Instances of a Module • We use counting abstraction to verify asynchronous composition of arbitrary number of instances of a module • Counting abstraction – Creates an integer variable for each local state of a module – Each variable counts the number of instances in a particular state – Parameterized constants are used to denote the number of instances of each module • Local variables of the module have to be finite domain – Shared variables can be unbounded • Counting abstraction is automated

Readers-Writers After Counting Abstraction Parameterized constants module main() introduced by the counting integer nr; abstraction boolean busy; parameterized integer num. Reader, num. Writer; restrict: nr>=0 and num. Reader>=0 and num. Writer>=0; initial: nr=0 and !busy; Variables introduced by the module Reader() counting abstraction integer reading. F, reading. T; initial: reading. F=num. Reader and reading. T=0; r. Enter: reading. F>0 and !busy and nr’=nr+1 and reading. F’=reading. F-1 and reading. T’=reading. T+1; r. Exit: reading. T>0 and nr’=nr-1 reading. T’=reading. T-1 and reading. F’=reading. F+1; Reader: r. Enter | r. Exit; endmodule Writer(). . . Denotes arbitrary number of endmodule instances main: Reader()* | Writer()*; spec: invariant(busy => nr=0) endmodule

Airport Ground Traffic Control Airplane[*] t 1 r 1 empty land[in(r 1. empty)]/taxii 1 E flow fly landing land/ taxii 1 E[in(t 1. empty)] /taxii 2 E takingoff taxiing 1 r 2 empty occupied taxii 1 E [in(t 1. empty)] /taxii 2 E occupied t 2 g empty parking empty occupied taxiing 2

Action Language Translation of Airport Ground Traffic Control module main() enumerated sr 1, sr 2, st 1, st 2, sg {empty, occupied}; open boolean land, taxii 1 E, taxii 2 W, fly, park, takeoff; enumerated state 1, state 2 {flow, landing, taxiing 1, taxiing 2, takingoff, parking}; initial: land !taxii 1 E and !taxii 2 W and !fly and !park and !takeoff; module Airplane(state) enumerated state {flow, landing, taxiing 1, taxiing 2, takingoff, parking}; initial: state=flow; a 1: state=flow and sr 1=empty and land state'=landing and !land' and taxii 1 E'; a 2: state=landing and st 1=empty and taxii 1 E and state'=taxiing 1 and !taxii 1 E' and taxii 2 E'; a 3: state=taxiing 1 and sr 2=empty and st 2=empty and sg=empty and taxii 2 E and state'=taxiing 2 and !taxii 2 E' and park'; . . . Airplane: a 1 | a 2 | a 3 | a 4 | a 5 | a 6 | a 7 ; endmodule

Action Language Translation of Airport Ground Traffic Control module main(). . . module Airplane(state). . . endmodule. . . module r 1() initial: sr 1=empty; r 11: sr 1=empty and land !land' and taxii 1 E' and sr 1'=occupied; r 12: sr 1=occupied and taxii 1 E and st 1=empty and sr 1'=empty and !taxii 1 E' and taxii 2 E'; r 1: r 11 | r 12; endmodule. . . main: ((Airplane(state 1) | Airplane(state 2)) & r 1() & t 1() & r 2() & t 2() & g() | Env. Event()) & Event. Constraint(); spec: AG(EX(true)) spec: AG(sr 1=occupied and st 1=occupied => AX(sr 1=occupied)) spec: AG(state 1=taxiing 2 => state 2!=taxiing 2) endmodule

Parameterized Version of Airport Ground Traffic Control module main(). . . integer taxiing 2 count; restrict: taxiing 2 count >= 0; initial: taxiing 2 count = 0; initial: land !taxii 1 E and !taxii 2 W and !fly and !park and !takeoff; module Airplane() enumerated state {flow, landing, taxiing 1, taxiing 2, takingoff, parking}; . . . Airplane: a 1 | a 2 | a 3 | a 4 | a 5 | a 6 | a 7 ; endmodule. . . main: (Airplane()* & r 1() & t 1() & r 2() & t 2() & g() | Env. Event()) & Event. Constraint(); spec: AG(EX(true)) spec: AG(sr 1=occupied and st 1=occupied => AX(sr 1=occupied)) spec: AG(taxiing 2 count <= 1) endmodule

Experiments Number of Airplanes Construction time (sec) Verification time (sec) Memory (MB) 2 0. 08 0. 02 1. 68 4 0. 21 0. 16 4. 63 8 0. 56 1. 08 15. 75 16 1. 34 3. 24 39. 80 32 3. 25 9. 69 64. 45 64 10. 25 26. 21 124. 35 P 41. 32 13. 85 15. 15

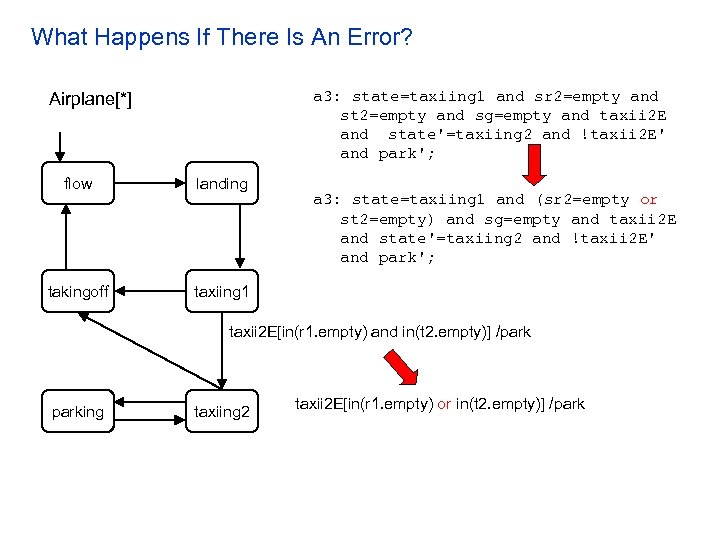What Happens If There Is An Error? a 3: state=taxiing 1 and sr 2=empty and st 2=empty and sg=empty and taxii 2 E and state'=taxiing 2 and !taxii 2 E' and park'; Airplane[*] flow landing takingoff taxiing 1 a 3: state=taxiing 1 and (sr 2=empty or st 2=empty) and sg=empty and taxii 2 E and state'=taxiing 2 and !taxii 2 E' and park'; taxii 2 E[in(r 1. empty) and in(t 2. empty)] /parking taxiing 2 taxii 2 E[in(r 1. empty) or in(t 2. empty)] /park

Action Language Verifier Generates a Counter-Example TEMPORAL PROPERTY AG(main. 0. state 1 = taxiing 2 => main. 0. state 2 != taxiing 2) COUNTER-EXAMPLE THE FORMULA EF(!(main. 0. state 1 = taxiing 2 => main. 0. state 2 != taxiing 2)) IS WITNESSED BY THE FOLLOWING PATH STATE 0 !main. 0. takeoff && !main. 0. park && !main. 0. fly && !main. 0. taxii 2 W && !main. 0. taxii 2 E && !main. 0. taxii 1 E && main. 0. land && main. 0. sg = empty && main. 0. st 2 = empty && main. 0. st 1 = empty && main. 0. sr 2 = empty && main. 0. sr 1 = empty && main. 0. state 2 = flow && main. 0. state 1 = flow PATH STATE 1 !main. 0. takeoff && !main. 0. park && !main. 0. fly && !main. 0. taxii 2 W && !main. 0. taxii 2 E && main. 0. taxii 1 E && !main. 0. land && main. 0. sg = empty && main. 0. st 2 = empty && main. 0. st 1 = empty && main. 0. sr 2 = empty && main. 0. sr 1 = occupied && main. 0. state 2 = flow && main. 0. state 1 = landing PATH STATE 2 !main. 0. takeoff && !main. 0. park && !main. 0. fly && !main. 0. taxii 2 W && main. 0. taxii 2 E && !main. 0. taxii 1 E && !main. 0. land && main. 0. sg = empty && main. 0. st 2 = empty && main. 0. st 1 = occupied && main. 0. sr 2 = empty && main. 0. sr 1 = empty && main. 0. state 2 = flow && main. 0. state 1 = taxiing 1

PATH STATE 3 !main. 0. takeoff && main. 0. park && !main. 0. fly && !main. 0. taxii 2 W && !main. 0. taxii 2 E && !main. 0. taxii 1 E && !main. 0. land && main. 0. sg = empty && main. 0. st 2 = occupied && main. 0. st 1 = empty && main. 0. sr 2 = empty && main. 0. sr 1 = empty && main. 0. state 2 = flow && main. 0. state 1 = taxiing 2 PATH STATE 4 !main. 0. takeoff && !main. 0. park && !main. 0. fly && !main. 0. taxii 2 W && !main. 0. taxii 2 E && !main. 0. taxii 1 E && main. 0. land && main. 0. sg = empty && main. 0. st 2 = occupied && main. 0. st 1 = empty && main. 0. sr 2 = empty && main. 0. sr 1 = empty && main. 0. state 2 = flow && main. 0. state 1 = taxiing 2 PATH STATE 5 !main. 0. takeoff && !main. 0. park && !main. 0. fly && !main. 0. taxii 2 W && !main. 0. taxii 2 E && main. 0. taxii 1 E && !main. 0. land && main. 0. sg = empty && main. 0. st 2 = occupied && main. 0. st 1 = empty && main. 0. sr 2 = empty && main. 0. sr 1 = occupied && main. 0. state 2 = landing && main. 0. state 1 = taxiing 2 PATH STATE 6 !main. 0. takeoff && !main. 0. park && !main. 0. fly && !main. 0. taxii 2 W && main. 0. taxii 2 E && !main. 0. taxii 1 E && !main. 0. land && main. 0. sg = empty && main. 0. st 2 = occupied && main. 0. st 1 = occupied && main. 0. sr 2 = empty && main. 0. sr 1 = empty && main. 0. state 2 = taxiing 1 && main. 0. state 1 = taxiing 2 PATH STATE 7 !main. 0. takeoff && main. 0. park && !main. 0. fly && !main. 0. taxii 2 W && !main. 0. taxii 2 E && !main. 0. taxii 1 E && !main. 0. land && main. 0. sg = empty && main. 0. st 2 = occupied && main. 0. st 1 = occupied && main. 0. sr 2 = empty && main. 0. sr 1 = empty && main. 0. state 2 = taxiing 2 && main. 0. state 1 = taxiing 2 THE FORMULA !(main. 0. state 1 = taxiing 2 => main. 0. state 2 != taxiing 2) IS SATISFIED BY THE STATE !main. 0. takeoff && main. 0. park && !main. 0. fly && !main. 0. taxii 2 W && !main. 0. taxii 2 E && !main. 0. taxii 1 E && !main. 0. land && main. 0. sg = empty && main. 0. st 2 = occupied && main. 0. st 1 = occupied && main. 0. sr 2 = empty &&

Time elapsed for transition system construction: 0. 07 seconds Time elapsed for counter-example generation: 0. 11 seconds Total heap memory used: 2314240 bytes

Related Work: Model Checking Software Specifications • [Atlee, Gannon 93] – Translating SCR mode transition tables to input language of explicit state model checker EMC [Clarke, Emerson, Sistla 86] • [Chan et al. 98, 00] – Translating RSML specifications to input language of SMV • [Bharadwaj, Heitmeyer 99] – Translating SCR specifications to Promela, input language of automata-theoretic explicit state model checker SPIN

Related Work: Constraint-Based Verification • [Cooper 71] – Used a decision procedure for Presburger arithmetic to verify sequential programs represented in a block form • [Cousot and Halbwachs 78] – Used real arithmetic constraints to discover invariants of sequential programs • [Halbwachs 93] – Constraint based delay analysis in synchronous programs • [Halbwachs et al. 94] – Verification of linear hybrid systems using constraint representations • [Alur et al. 96] – Hy. Tech, a model checker for hybrid systems

Related Work: Constraint-Based Verification • [Boigelot and Wolper 94] – Verification with periodic sets • [Boigelot et al. ] – Meta-transitions, accelerations • [Delzanno and Podelski 99] – Built a model checker using constraint logic programming framework • [Boudet Comon], [Wolper and Boigelot ‘ 00] – Translating linear arithmetic constraints to automata

Related Work: Automata-Based Representations • [Klarlund et al. ] – MONA, an automata manipulation tool for verification • [Boudet Comon] – Translating linear arithmetic constraints to automata • [Wolper and Boigelot ‘ 00] – verification using automata as a symbolic representation • [Kukula et al. 98] – application of automata based verification to hardware verification

Related Work: Combining Symbolic Representations • [Chan et al. CAV’ 97] – both linear and non-linear constraints are mapped to BDDs – Only data-memoryless and data-invariant transitions are supported • [Bharadwaj and Sims TACAS’ 00] – Combines automata based representations (for linear arithmetic constraints) with BDDs – Specialized for inductive invariant checking • [Bensalem et al. 00] – Symbolic Analysis Laboratory – Designed a specification language that allows integration of different verification tools

Related Work: Tools • LASH [Boigelot et al] – Automata based – Experiments show it is significantly slower than ALV • BRAIN [Rybina et al] – Uses Hilbert’s basis as a symbolic representation – Limited functionality • FAST [Leroux et al] – Also implemented on top of MONA – Supports acceleration and manual strategies • TREX [Bouajjani et al] – Reachability analysis, timed systems, multiple domains