Векторы в пространстве К Основные определения и понятия

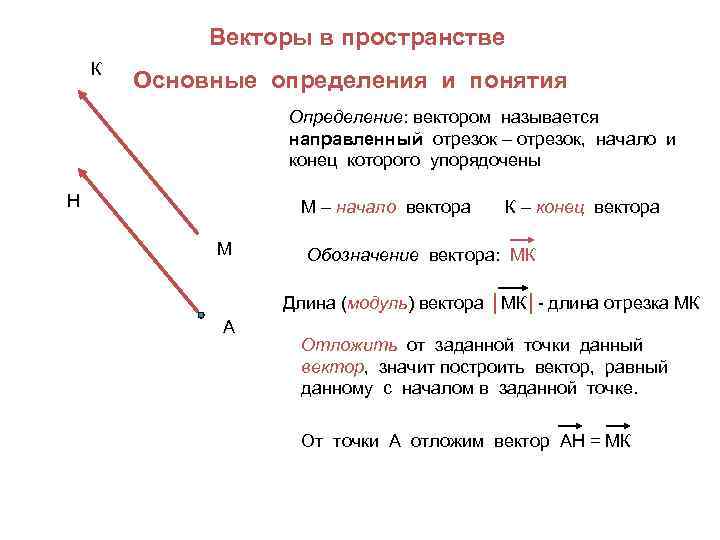Векторы в пространстве К Основные определения и понятия Определение: вектором называется направленный отрезок – отрезок, начало и конец которого упорядочены Н М – начало вектора М К – конец вектора Обозначение вектора: МК Длина (модуль) вектора │МК│- длина отрезка МК А Отложить от заданной точки данный вектор, значит построить вектор, равный данному с началом в заданной точке. От точки А отложим вектор АН = МК

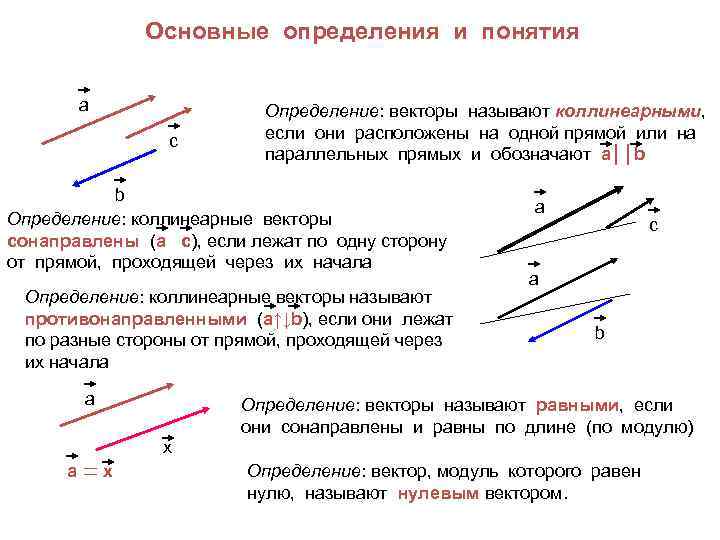Основные определения и понятия a c Определение: векторы называют коллинеарными, если они расположены на одной прямой или на параллельных прямых и обозначают а││b b Определение: коллинеарные векторы сонаправлены (а с), если лежат по одну сторону от прямой, проходящей через их начала Определение: коллинеарные векторы называют противонаправленными (а↑↓b), если они лежат по разные стороны от прямой, проходящей через их начала a a c a b Определение: векторы называют равными, если они сонаправлены и равны по длине (по модулю) х a х Определение: вектор, модуль которого равен нулю, называют нулевым вектором.

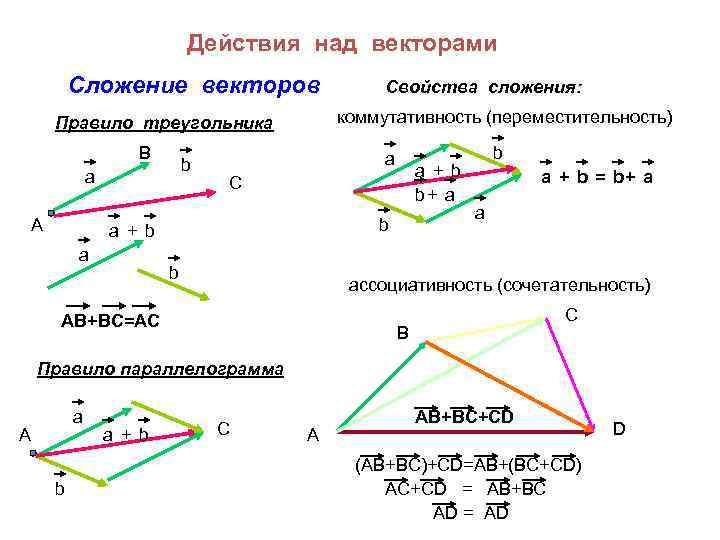Действия над векторами Сложение векторов коммутативность (переместительность) Правило треугольника В b a А a a + b b+ a С b a + b a Свойства сложения: b b a + b = b+ a a ассоциативность (сочетательность) АВ+ВС=АС С В Правило параллелограмма a А b a + b С А AB+BC+CD (AB+BC)+CD=AB+(BC+CD) AC+CD = AB+BC AD = AD D

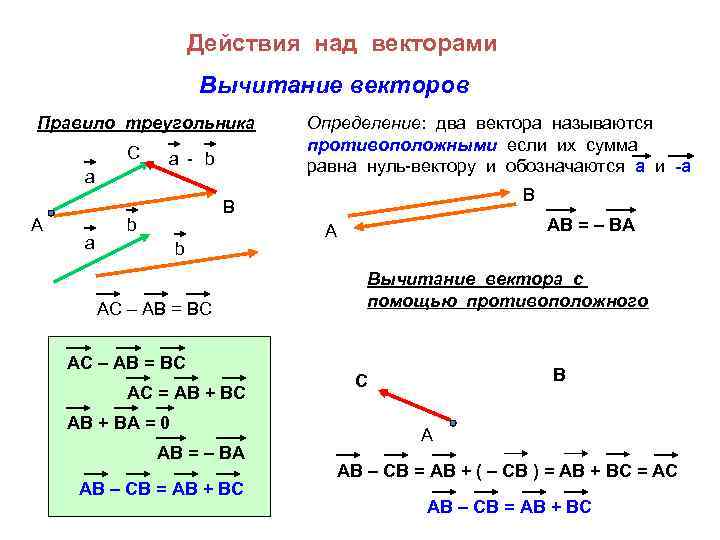Действия над векторами Вычитание векторов Правило треугольника C a А a a - b Определение: два вектора называются противоположными если их сумма равна нуль-вектору и обозначаются а и -а В B b b AC – AB = BC АС = АВ + ВС АВ + ВА = 0 АВ = – ВА АВ – СВ = АВ + ВС АВ = – ВА А Вычитание вектора с помощью противоположного В С А АВ – СВ = АВ + ( – СВ ) = АВ + ВС = АС АВ – СВ = АВ + ВС

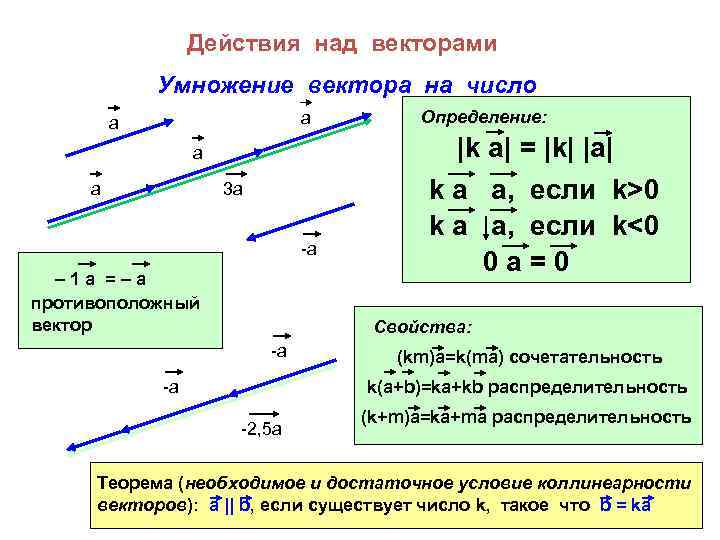Действия над векторами Умножение вектора на число a a 3 a -a – 1 a =–a противоположный вектор Определение: |k a| = |k| |a| k a a, если k>0 k a a, если k<0 0 a=0 Свойства: -a -a (km)a=k(ma) сочетательность k(a+b)=ka+kb распределительность -2, 5 a (k+m)a=ka+ma распределительность Теорема (необходимое и достаточное условие коллинеарности векторов): а || b, если существует число k, такое что b = ka

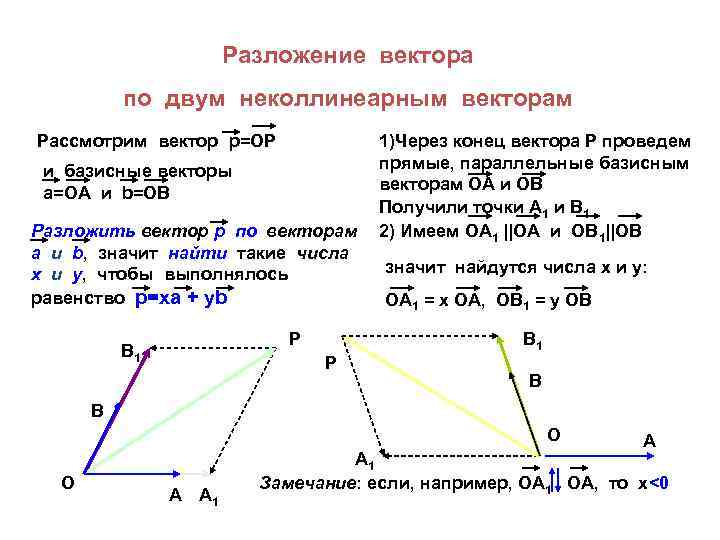Разложение вектора по двум неколлинеарным векторам Рассмотрим вектор p=OP и базисные векторы а=ОА и b=OB Разложить вектор р по векторам а и b, значит найти такие числа х и у, чтобы выполнялось равенство р=ха + уb P В 1 1)Через конец вектора Р проведем прямые, параллельные базисным векторам ОА и ОВ Получили точки А 1 и В 1 2) Имеем ОА 1 ||ОА и ОВ 1||ОВ значит найдутся числа х и у: ОА 1 = х ОА, ОВ 1 = у ОВ B 1 P B В O O А А 1 A A 1 Замечание: если, например, ОА 1 ОА, то х<0

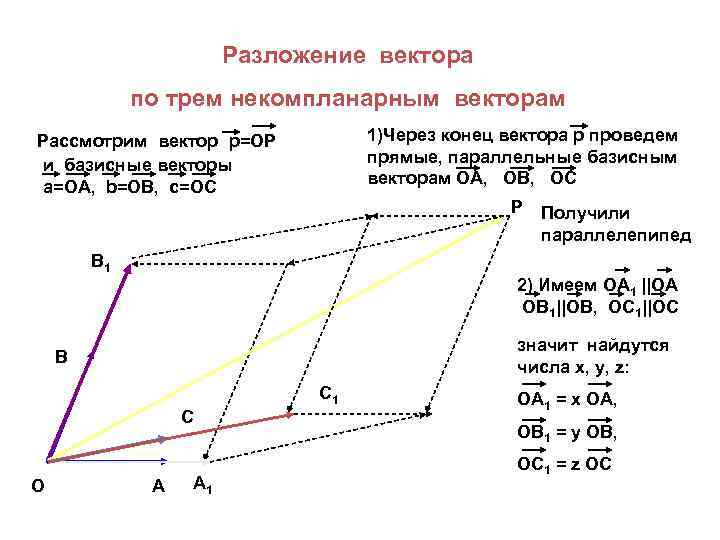Разложение вектора по трем некомпланарным векторам 1)Через конец вектора р проведем прямые, параллельные базисным векторам ОА, ОВ, ОС Рассмотрим вектор p=OP и базисные векторы а=ОА, b=OB, c=OC P Получили параллелепипед В 1 2) Имеем ОА 1 ||ОА ОВ 1||ОВ, OC 1||OC значит найдутся числа х, у, z: В C 1 C O А А 1 ОА 1 = х ОА, ОВ 1 = у ОВ, OC 1 = z OC

Действия над векторами Скалярное умножение векторов Определение: скалярным произведением векторов а и b называется произведение длин этих векторов на косинус угла между ними a · b=|a| · |b| · cos(a, b) Скалярное произведение векторов это число. Необходимое и достаточное условие равенства скалярного произведения нулю a · b = 0 <=> a=0 b=0 a┴b Свойства скалярного произведения: a·b=b·a переместительность (ka) · b = k(a · b) сочетательность (a + b) · c = a · c + b · c распределительность а 2= | а | 2 скалярный квадрат взаимная перпендикулярность ненулевых векторов