ВЕКТОРЫ ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ СКАЛЯРНОЕ ВЕКТОРНОЕ И

ВЕКТОРЫ. ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ. СКАЛЯРНОЕ, ВЕКТОРНОЕ И СМЕШАННОЕ ПРОИЗВЕДЕНИЯ ВЕКТОРОВ.

Скалярные и векторные величины. • • • , . • • • Величины, которые характеризуются лишь числовым значением (например: температура, масса, время, площадь, объем и др. ), называются скалярными или скалярами. Величины, которые характеризуются не только числом, но и направлением, называются векторными. Вектором называется направленный отрезок. Обозначение: или. В А Точка А – начало вектора, точка В – конец вектора. Длиной или модулем вектора называется длина отрезка АВ. Обозначение: Вектор, длина которого равна единице называется единичным. Единичный вектор, направление которого совпадает с направлением вектора , называется ортом вектора. Обозначение: .

• Два вектора и называются коллинеарными, если они лежат на одной или параллельных прямых. Обозначение: • Три вектора называются компланарными, если они лежат на одной или на параллельных плоскостях. • Два вектора называются равными, если они коллинеарные, сонаправленые и их длины равны.

Линейные операции над векторами • Суммой векторов и называется третий вектор , начало которого совпадает с началом первого вектора, а конец - с концом второго, при условии, что второй вектор приложен к концу первого. Правило треугольника: Правило параллелограмма:

• Разностью двух векторов и называется третий вектор идущий из конца второго вектора в конец первого, при условии, что оба вектора приложены в одну точку. В параллелограмме, построенном на векторах и , одна направленная диагональ является суммой данных векторов, а другая – их разностью. ,

• Произведением вектора на число называется вектор , коллинеарный вектору , длина его равна , а направление совпадает с направлением вектора , если и противоположно направлению вектора , если.

• Свойства линейных операций: 1) 2) 3) 4) 5) Эти свойства позволяют проводить преобразования в линейных операциях с вектором так, как это делается в обычной алгебре: слагаемые менять местами, вводить скобки, группировать, выносить за скобки скалярные, так и векторные общие множители.

Проекция вектора на ось • • • Проекцией точки М на ось l называется основание N перпендикуляра МN, опущенного из точки на ось. Проекцией вектора на ось l называется число , если вектор и ось l одинаково направлены, и , если их направления противоположны. Обозначение: В А С D l Проекция вектора на ось l равна произведению модуля этого вектора на косинус угла между вектором и осью: Свойство 1. Проекция суммы нескольких векторов на одну и ту же ось равна сумме их проекций на эту ось. Свойство 2. При умножении вектора на число его проекция умножается на это число.

Прямоугольная система координат • Прямоугольная система координат на плоскости: У ОХ – ось абсцисс, ОУ – ось ординат N М - радиус вектор точки М j • O i Проекции вектора: Х P на оси координат называются координатами этого Т. е. • Единичные векторы i и j , направления которых совпадает с направлением осей координат называются ортами. • Разложение вектора по ортам: Если , то

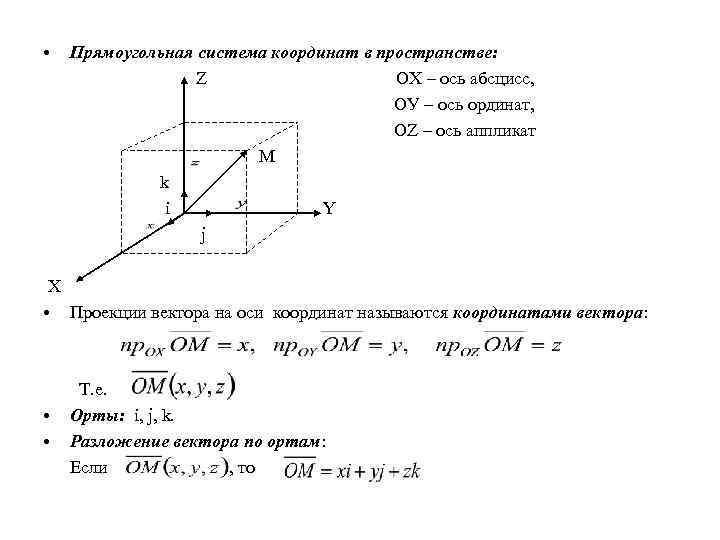• Прямоугольная система координат в пространстве: Z OX – ось абсцисс, ОУ – ось ординат, OZ – ось аппликат M k i Y j X • Проекции вектора на оси координат называются координатами вектора: • • Т. е. Орты: i, j, k. Разложение вектора по ортам: Если , то

Координаты вектора. Модуль вектора Пусть даны точки . Найдем координаты вектора Т. е. координаты вектора будут равны: или: Модуль вектора равен: или: Если , то

Линейные операции над векторами в координатной форме Если векторы и заданы своими координатами, т. е. то при сложении этих векторов их одноименные координаты складываются: При умножении вектора на число его координаты умножаются на то же число: Из последних двух формул следует, что Два вектора коллинеарны, если , тогда или Это есть условие коллинеарности двух векторов.

Направляющие косинусы вектора Направление вектора определяются углами , образованными им с осями координат ОХ, ОУ, ОZ. Косинусы этих углов называются направляющими косинусами вектора и определяются формулами Направляющие косинусы вектора связаны соотношением

Скалярное произведение векторов Скалярным произведением двух векторов и называется число, равное произведению модулей этих векторов на косинус угла между ними: Заметим, что Откуда проекция вектора , следовательно. на вектор будет равна: Свойства скалярного произведения: 1) 2) 3) 4) , если векторы перпендикулярны 5) , если 6) 7) ,

Скалярное произведение в координатной форме Если векторы и заданы своими координатами то: 1) 2) 3) если векторы перпендикулярны, то 4) угол между векторами равен

Векторное произведение векторов Тройка векторов , и называется правой, если кратчайший поворот от первого вектора ко второму совершается против часовой стрелки, если смотреть с конца третьего вектора. В противном случае тройка векторов называется левой. Векторным произведением вектора на вектор называется вектор , обозначаемый символом и определяемый следующими тремя условиями: 1) 2) вектор 3) тройка векторов перпендикулярен векторам , и и является правой. ;

Свойства векторного произведения Векторное произведение обладает следующими свойствами: 1) Если векторы коллинеарны, то 2) 3) Модуль векторного произведения равен площади параллелограмма, построенного на векторах и : 4) 5) 6)

Векторное произведение в координатной форме Если векторы заданы через координаты векторное произведение и определяется формулой: или Пример. Найти векторное произведение векторов Решение. , то