ВЕКТОРЫ И ДЕЙСТВИЯ НАД НИМИ 1 2 3

ВЕКТОРЫ И ДЕЙСТВИЯ НАД НИМИ 1. 2. 3. Основные понятия. Линейные операции над векторами. Нелинейные операции над векторами.

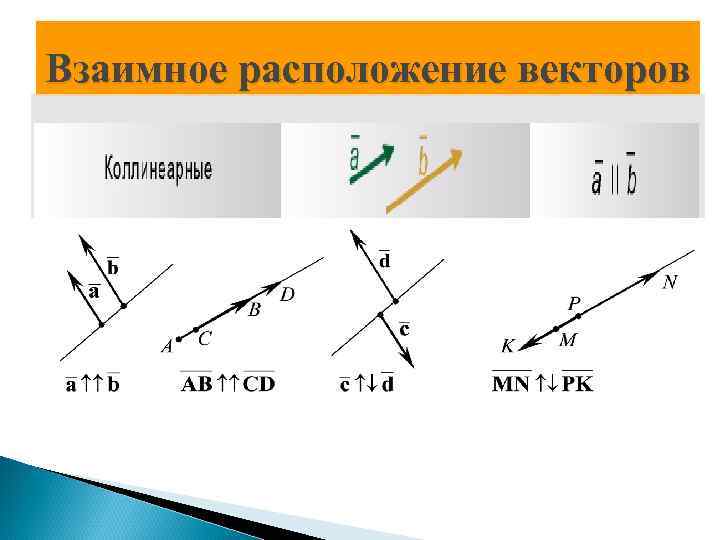Взаимное расположение векторов

Взаимное расположение векторов

Условия взаимного расположения векторов

Линейные операции над векторами № Геометрический образ 1. СЛОЖЕНИЕ ВЕКТОРОВ а) правило треугольника: в а а + в б) правило параллелограмма: а а в + в Координатная форма записи а + в = (ах + bx; аy + by ; аz + bz)

№ Геометрический образ 2. ВЫЧИТАНИЕ ВЕКТОРОВ а а в Координатная форма записи а в = (ах bx; аy by ; аz bz) в 3. УМНОЖЕНИЕ ВЕКТОРА НА ДЕЙСТВИТЕЛЬНОЕ ЧИСЛО k k a a k a = (kах; kаy; kаz)

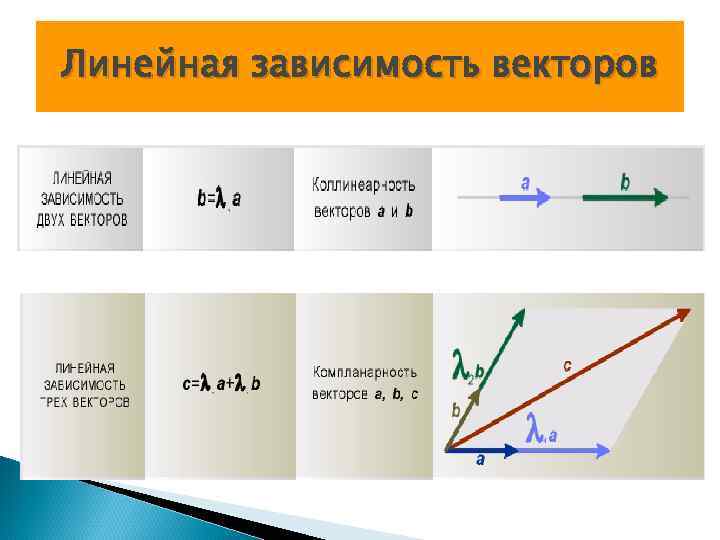Линейная зависимость векторов

Примеры: № 1. Найти длины диагоналей параллелограмма, построенного на векторах: = (3; -5; 8) и = (-1; 1; -4). № 2. Даны четыре точки. векторы , , , . Выяснить, коллинеарны ли и ?

НЕЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ скалярное произведение двух векторов; векторное произведение двух векторов; смешанное произведение трех векторов

Скалярное произведение двух векторов

Свойства скалярного произведения 1. (переместительное); 2. (сочетательное); 3. (распределительное); 4. 5. ; (условие перпендикулярности векторов) ;

Векторное произведение двух векторов

Свойства векторного произведения 1. 2. 3. 4. (условие коллинеарности) 1.

Смешанное произведение трех векторов

Свойства смешанного произведения ; 1. 2. 3. 4. если три данных вектора компланарны, то (и наоборот); ;

Приложения нелинейных операций над векторами Геометрические приложения Скалярное произведение

Приложения нелинейных операций над векторами Геометрические приложения Векторное произведение

Приложения нелинейных операций над векторами Геометрические приложения Смешанное произведение

Спасибо за внимание