Векторы 1 Понятие вектора 2 Сложение

Векторы § 1. Понятие вектора § 2. Сложение и вычитание векторов § 3. Умножение вектора на число. Применение векторов к решению задач

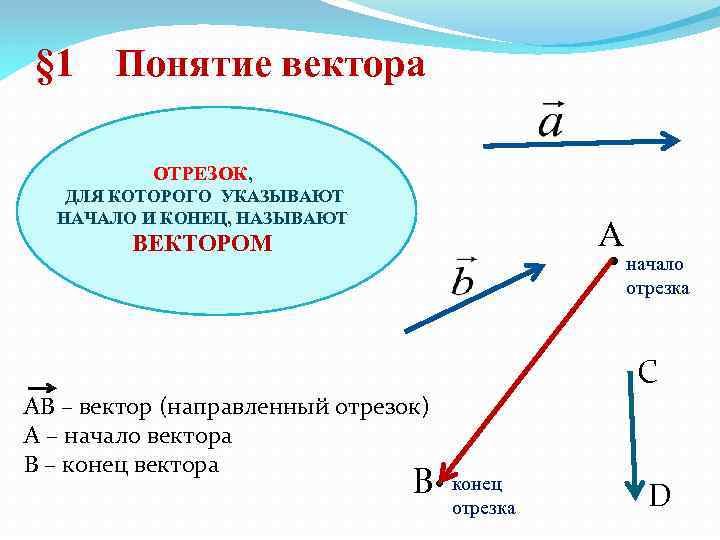§ 1 Понятие вектора ОТРЕЗОК, ДЛЯ КОТОРОГО УКАЗЫВАЮТ НАЧАЛО И КОНЕЦ, НАЗЫВАЮТ A • начало ВЕКТОРОМ отрезка С АВ – вектор (направленный отрезок) А – начало вектора В – конец вектора B • конец отрезка D

Длиной или модулем ненулевого вектора АВ называют длину отрезка АВ (или расстояние от точки А до В) Длина нулевого вектора |0| = 0 • A • B

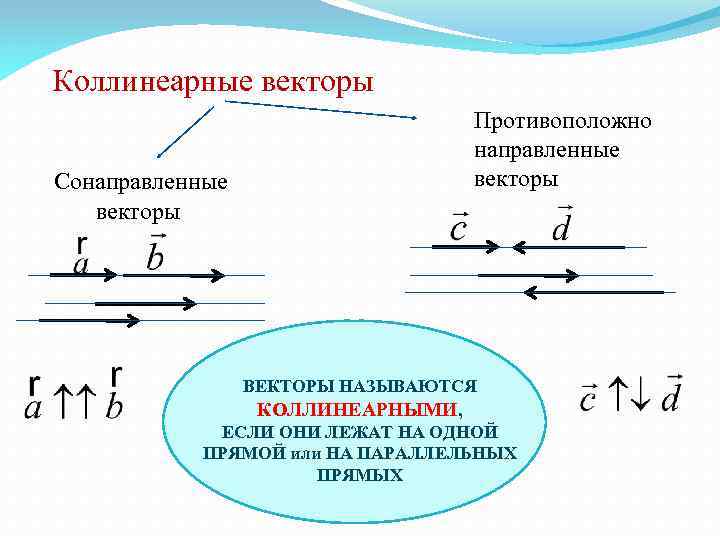Коллинеарные векторы Сонаправленные векторы Противоположно направленные векторы ВЕКТОРЫ НАЗЫВАЮТСЯ КОЛЛИНЕАРНЫМИ, ЕСЛИ ОНИ ЛЕЖАТ НА ОДНОЙ ПРЯМОЙ или НА ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ

ВЕКТОРЫ НАЗЫВАЮТСЯ РАВНЫМИ, ЕСЛИ ОНИ СОНАПРАВЛЕНЫ И ИХ ДЛИНЫ ОДИНАКОВЫ.

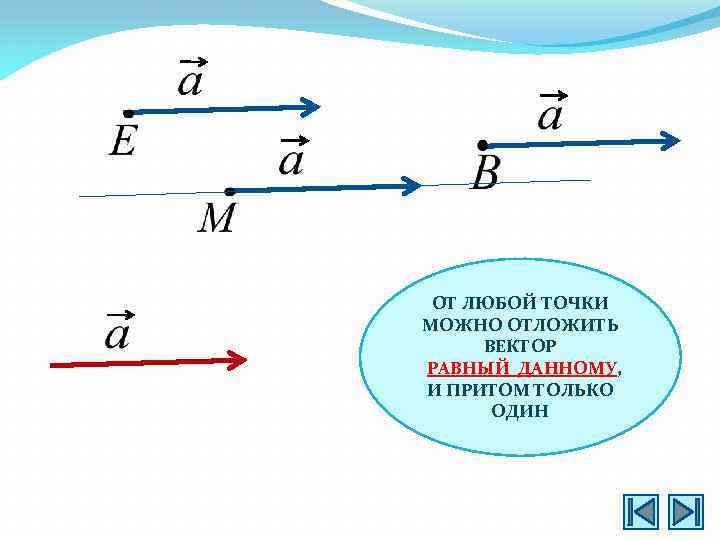ОТ ЛЮБОЙ ТОЧКИ МОЖНО ОТЛОЖИТЬ ВЕКТОР РАВНЫЙ ДАННОМУ, И ПРИТОМ ТОЛЬКО ОДИН

СЛОЖЕНИЕ И ВЫЧИТАНИЕ ВЕКТОРОВ

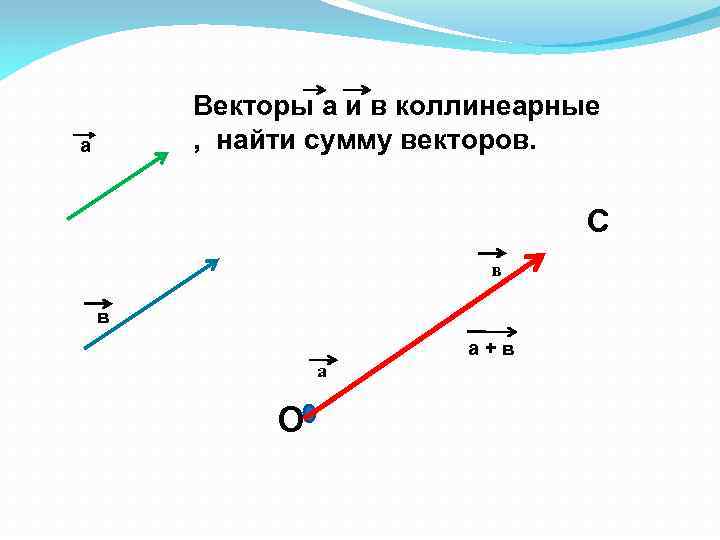Векторы а и в коллинеарные , найти сумму векторов. а С в в а+в а О

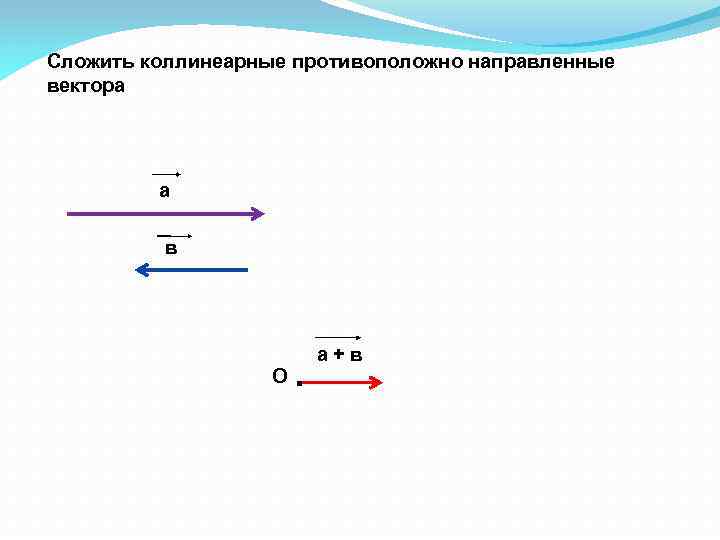Сложить коллинеарные противоположно направленные вектора а в О . а+в

ПРАВИЛО ТРЕУГОЛЬНИКА в в а а а+в 1) От конца вектора а отложить вектор в, равный вектору в ; 2) Провести вектор из начала вектора а в конец вектора в. 3) ВЫВОД: полученный вектор и будет суммой векторов а и в.

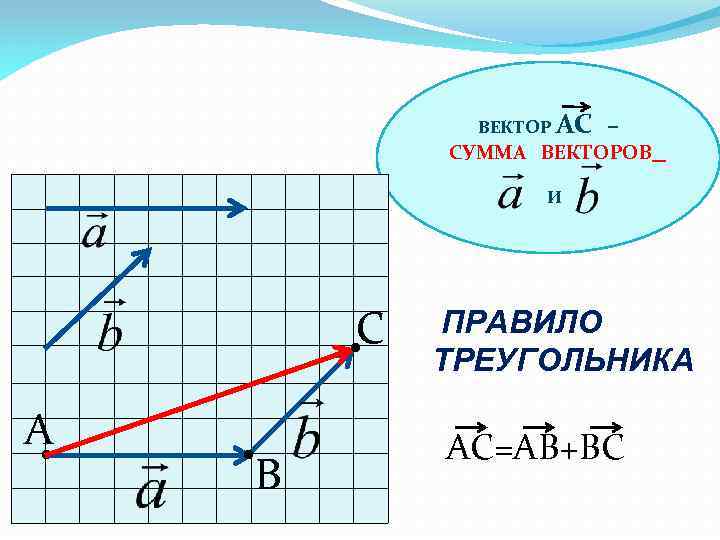ВЕКТОР АС – СУММА ВЕКТОРОВ И С • A • • B ПРАВИЛО ТРЕУГОЛЬНИКА AС=АВ+ВС

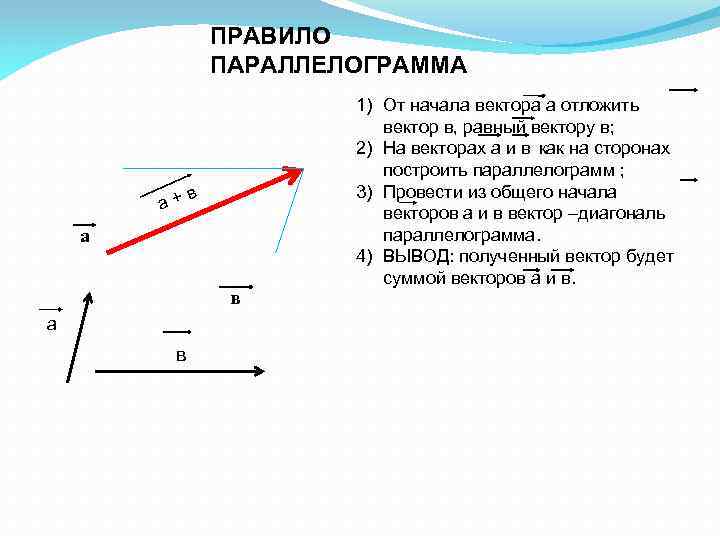ПРАВИЛО ПАРАЛЛЕЛОГРАММА а+ в а в 1) От начала вектора а отложить вектор в, равный вектору в; 2) На векторах а и в как на сторонах построить параллелограмм ; 3) Провести из общего начала векторов а и в вектор –диагональ параллелограмма. 4) ВЫВОД: полученный вектор будет суммой векторов а и в.

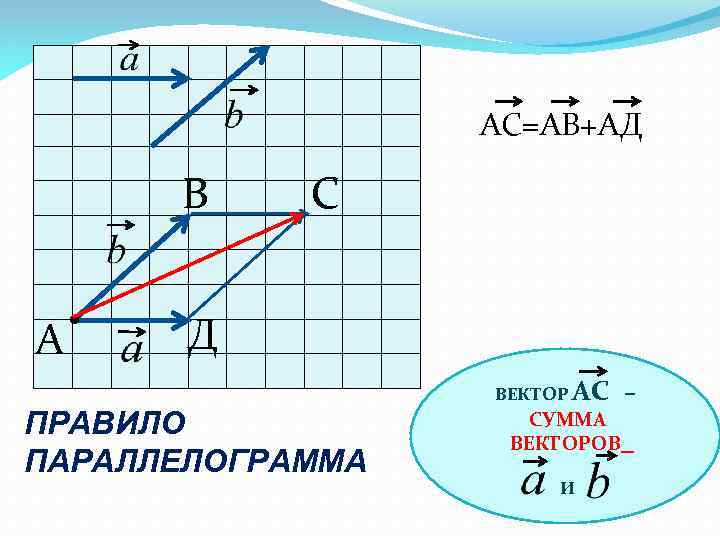AС=АВ+АД B A • С Д ПРАВИЛО ПАРАЛЛЕЛОГРАММА ВЕКТОР АС СУММА ВЕКТОРОВ И –

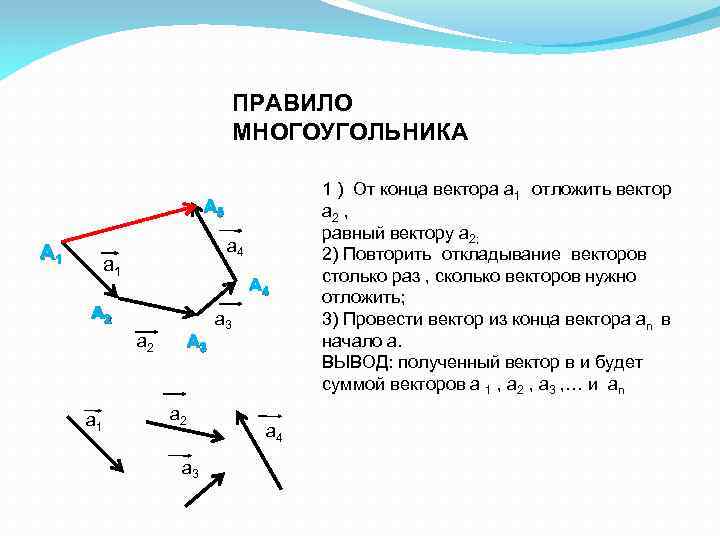ПРАВИЛО МНОГОУГОЛЬНИКА А 5 А 1 а 4 а 1 А 4 А 2 а 1 А 3 а 2 а 3 а 4 1 ) От конца вектора а 1 отложить вектор а 2 , равный вектору а 2; 2) Повторить откладывание векторов столько раз , сколько векторов нужно отложить; 3) Провести вектор из конца вектора аn в начало а. ВЫВОД: полученный вектор в и будет суммой векторов а 1 , а 2 , а 3 , … и аn

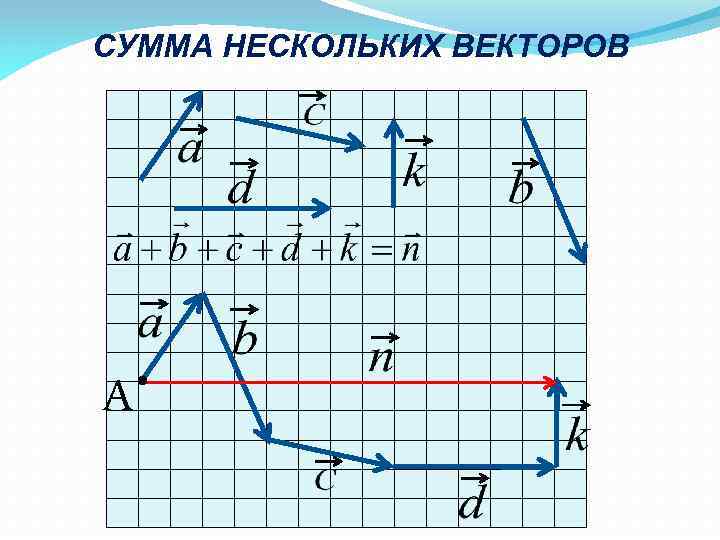СУММА НЕСКОЛЬКИХ ВЕКТОРОВ • A

При сложении нескольких векторов сумма данных векторов может быть равна нулевому вектору, если начало первого вектора совпадает с концом последнего вектора.

ЗАКОНЫ СЛОЖЕНИЯ ВЕКТОРОВ Для любых векторов а , в и с справедливы равенства: 1) а + в = в + а --- переместительный закон 2) ( а + в ) + с = а + ( в + с ) --- сочетательный закон

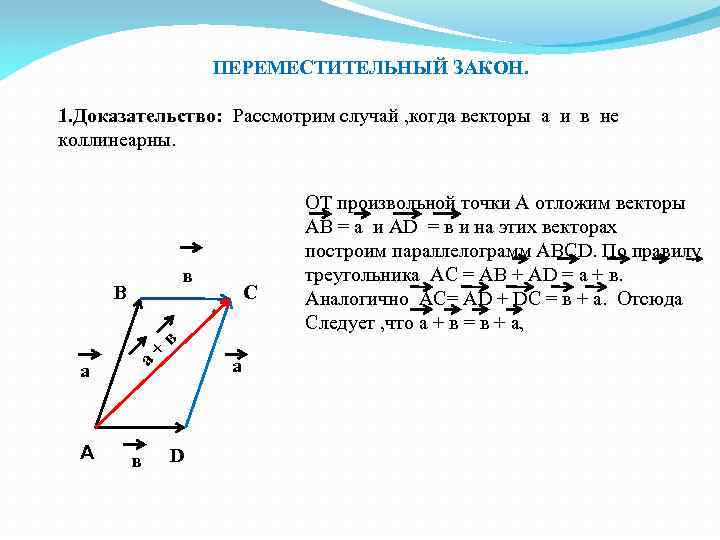ПЕРЕМЕСТИТЕЛЬНЫЙ ЗАКОН. 1. Доказательство: Рассмотрим случай , когда векторы а и в не коллинеарны. в В а а А в + С в а D ОТ произвольной точки А отложим векторы АВ = а и АD = в и на этих векторах построим параллелограмм АВСD. По правилу треугольника АС = АВ + АD = а + в. Аналогично АС= АD + DС = в + а. Отсюда Следует , что а + в = в + а,

2. СОЧЕТАТЕЛЬНЫЙ ЗАКОН. Доказательство. От произвольной точки А отложим вектор АВ = а , а от точки В вектор ВС = в , от точки С вектор СD=с. Применяя правило треугольника , получаем: (а + в ) + с = ( АВ + ВС )+ СD =АC+СD =АD а + ( в + с) = АВ + (ВС + СD)=АВ + ВС = А D. Отсюда следует , что ( а + в ) + с = а + ( в + с). Теорема доказана. В а . А в С с D

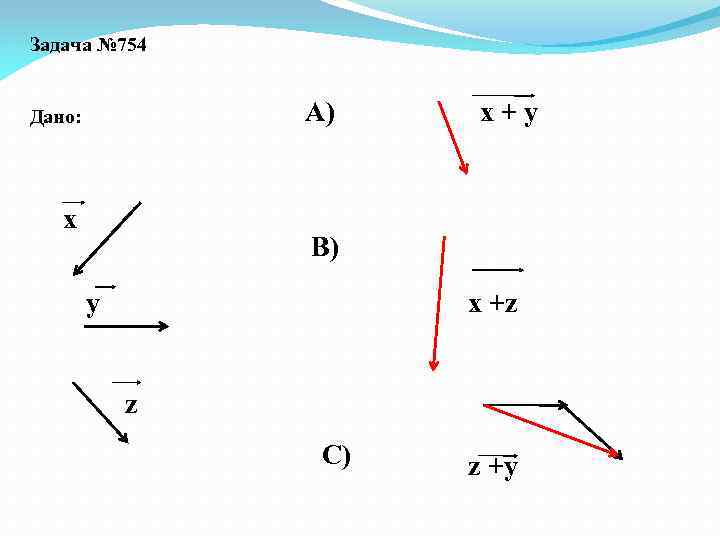Задача № 754 А) Дано: х х+y В) у x +z z C) z +y

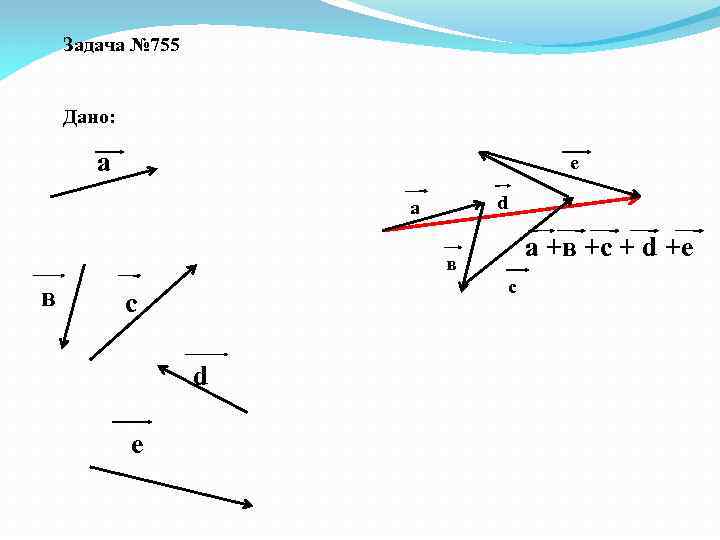Задача № 755 Дано: а e d а а +в +с + d +е в в с с d е

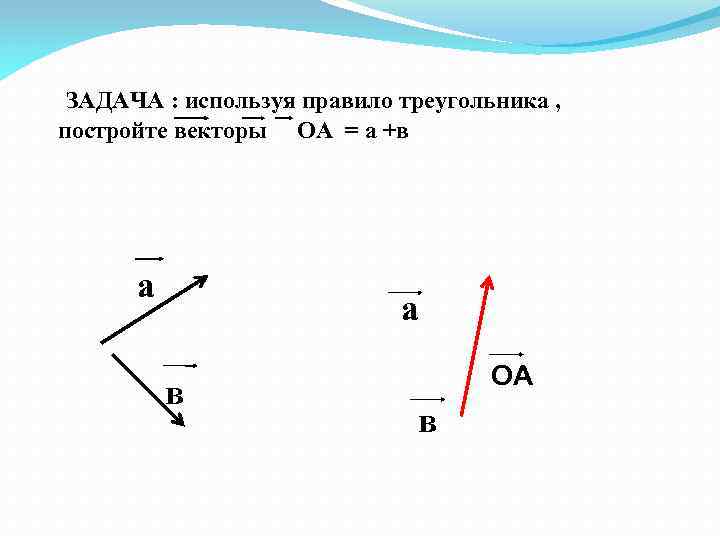ЗАДАЧА : используя правило треугольника , постройте векторы ОА = а +в а а в ОА в

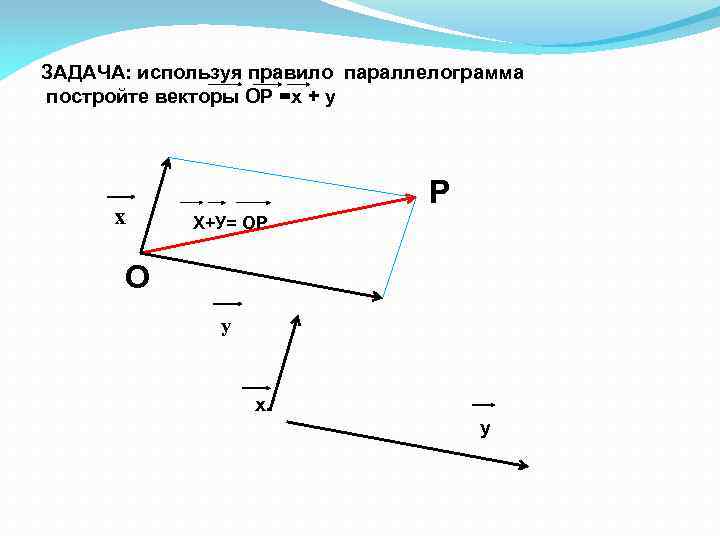ЗАДАЧА: используя правило параллелограмма постройте векторы ОР =х + у х P Х+У= ОР O у х. у

Задача: Используя правило треугольника, найдите сумму векторов: а) РМ и МТ, б) СН и НС, в) АВ + 0, г) 0 +СЕ. Решение: а)РМ + МТ = РТ б) СН +НС= СС= 0 в) АВ + 0 = АВ г) 0 + СЕ= СЕ

Д/З: п. 82 -84, № 753, 759(б), 763(б, в)

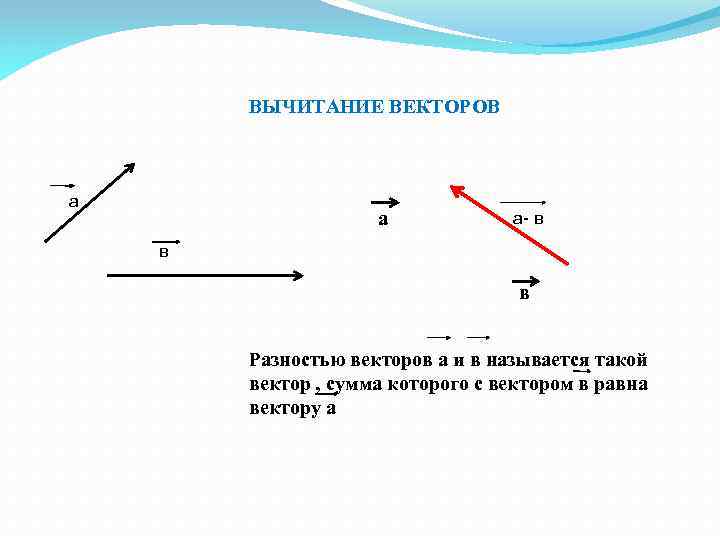ВЫЧИТАНИЕ ВЕКТОРОВ а а а- в в в Разностью векторов а и в называется такой вектор , сумма которого с вектором в равна вектору а

Теорема: Для любых векторов а и в справедливо равенство а – в = а +( - в ). Доказательство. По определению разности векторов ( а – в ) + в =а. Прибавив к обеим частям этого равенства вектор (-в), получим (а – в ) + в + (-в)= а+ (-в), или (а – в ) +0=(-в), откуда а – в = а + (-в). -в В а в а -в . О А а

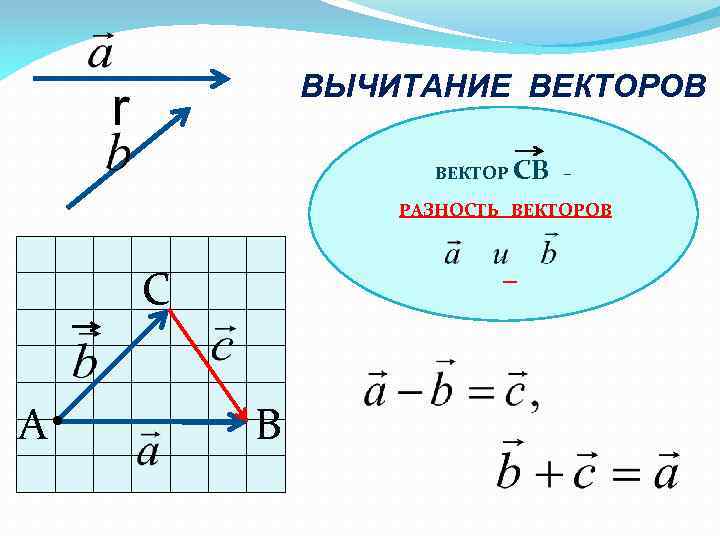ВЫЧИТАНИЕ ВЕКТОРОВ ВЕКТОР СВ – РАЗНОСТЬ ВЕКТОРОВ С А • B

ВЕКТОРЫ И ПРОТИВОПОЛОЖНЫЕ ВЕКТОРЫ

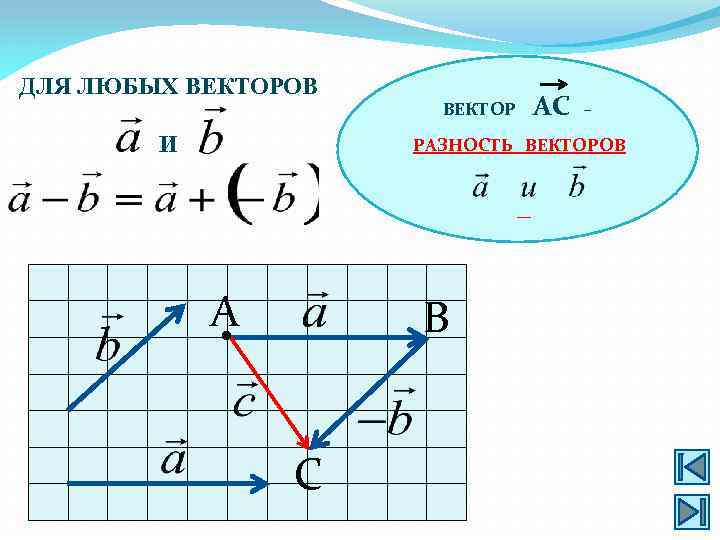ДЛЯ ЛЮБЫХ ВЕКТОРОВ И ВЕКТОР АС – РАЗНОСТЬ ВЕКТОРОВ А B • С

3. Упростите выражения: 1) ; 2). Решение Используем законы сложения векторов: 1)

Найдите вектор из условий: 1) ; 2) Решение Используем законы сложения векторов: или же , тогда

Д/З: п. 82 -85, № 761 без чертежа, 762, 764(а)