Вектор1.pptx
- Количество слайдов: 51

Векторная алгебра

Вектором называется упорядоченная пара точек, первая точка называется началом вектора, вторая – концом вектора. Расстояние между начальной и конечной точкам вектора называется его длиной, или модулем вектора. Вектор можно определить как направленный отрезок прямой имеющей начальную и конечную точки, поэтому определяющим для всякой векторной величины будет направление и значение. Вектор с началом в точке и концом в точке обозначают , начало вектора при этом называют точкой приложения. Если начало и конец вектора не задаются непосредственно, то вектор обозначают. Длина вектора обозначается или соединяющий начало и конец вектора. , или Чтобы задать вектор, необходимо указать: • его начальную и конечную точки, или • прямую; • направление на этой прямой; • начальную и конечную точки вектора на 13. 12. 2010 Р. Мунипов этой прямой. , как отрезок прямой 2

Вектор, начало и конец которого совпадают, называют нулевым вектором, его длина равна нулю. Очевидно, нулевой вектор есть точка, и он не имеет направления. Длина нулевого вектора равна нулю. Каждую точку пространства можно интерпретировать как нулевой вектор. 13. 12. 2010 Р. Мунипов 3

Два вектора называются равными если они имеют одинаковое направление и равные модули. Очевидно, два вектора равны если один из них параллельным переносом можно совместить с другим так, что их начальная и конечная точки совпадут. Значит данный вектор можно переносить, не меняя его направления и длины в любую точку пространства, при этом получаемые векторы будут равны исходному ПРИНЦИП СВОБОДНОГО ВЕКТОРА. Вектор не меняется при его параллельном переносе с сохранением исходного направления и длины. Вектор удовлетворяющий принципу свободного вектора называют свободным вектором. 13. 12. 2010 Р. Мунипов 4

Отношение равенства векторов является отношением эквивалентности алгебраических структур: а) каждый вектор равен самому себе (рефлексивность); б) если вектор равен вектору , то и вектор равен вектору (симметричность); в) если вектор равен вектору , то вектор равен вектору (транзитивность). Для любой точки и любого вектора существует единственная точка , для которой справедливо. Таким образом, любой вектор ставит в соответствие каждой точке единственную точку такую, что. Такое соответствие между точкой -вектором и точкой называют параллельным переносом. Поэтому свободные вектор отождествляют с параллельным переносом. 13. 12. 2010 Р. Мунипов 5
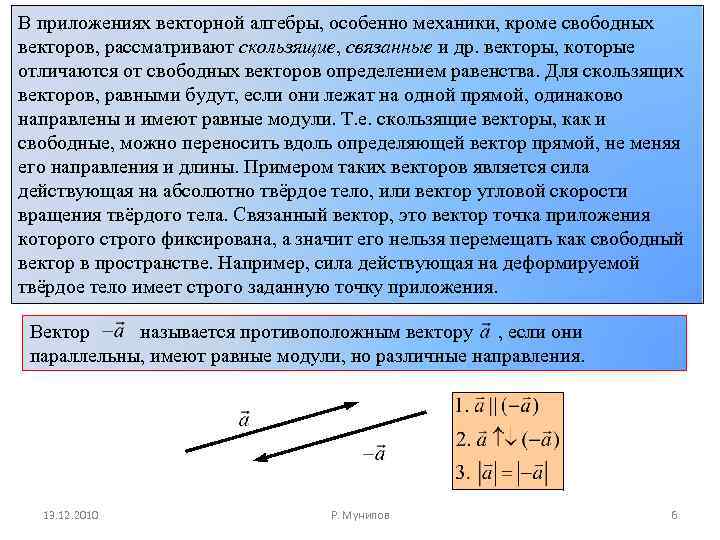
В приложениях векторной алгебры, особенно механики, кроме свободных векторов, рассматривают скользящие, связанные и др. векторы, которые отличаются от свободных векторов определением равенства. Для скользящих векторов, равными будут, если они лежат на одной прямой, одинаково направлены и имеют равные модули. Т. е. скользящие векторы, как и свободные, можно переносить вдоль определяющей вектор прямой, не меняя его направления и длины. Примером таких векторов является сила действующая на абсолютно твёрдое тело, или вектор угловой скорости вращения твёрдого тела. Связанный вектор, это вектор точка приложения которого строго фиксирована, а значит его нельзя перемещать как свободный вектор в пространстве. Например, сила действующая на деформируемой твёрдое тело имеет строго заданную точку приложения. Вектор называется противоположным вектору , если они параллельны, имеют равные модули, но различные направления. 13. 12. 2010 Р. Мунипов 6
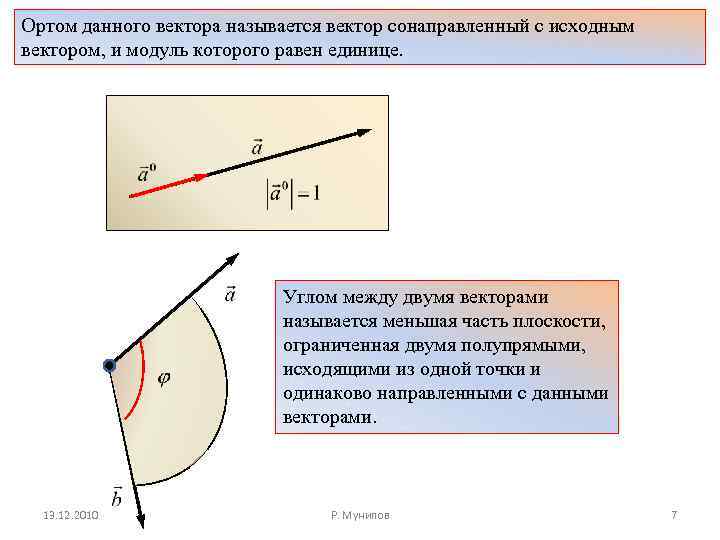
Ортом данного вектора называется вектор сонаправленный с исходным вектором, и модуль которого равен единице. Углом между двумя векторами называется меньшая часть плоскости, ограниченная двумя полупрямыми, исходящими из одной точки и одинаково направленными с данными векторами. 13. 12. 2010 Р. Мунипов 7
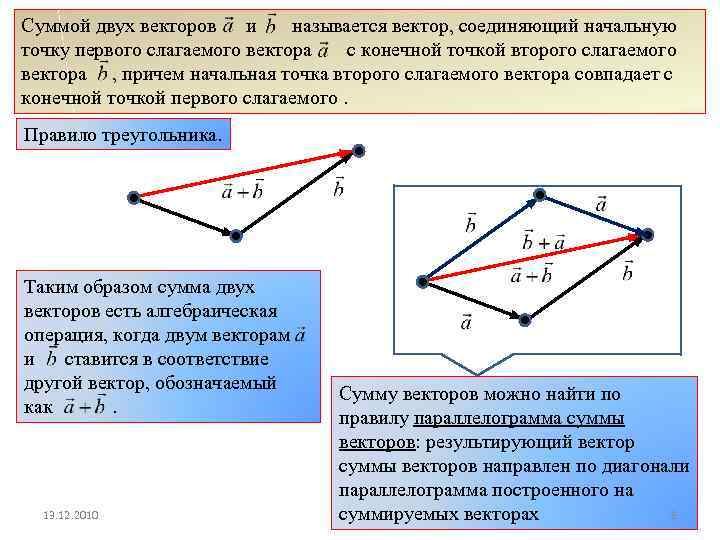
Суммой двух векторов и называется вектор, соединяющий начальную точку первого слагаемого вектора с конечной точкой второго слагаемого вектора , причем начальная точка второго слагаемого вектора совпадает с конечной точкой первого слагаемого. Правило треугольника. Таким образом сумма двух векторов есть алгебраическая операция, когда двум векторам и ставится в соответствие другой вектор, обозначаемый как. 13. 12. 2010 Сумму векторов можно найти по правилу параллелограмма суммы векторов: результирующий вектор суммы векторов направлен по диагонали параллелограмма построенного на Р. суммируемых векторах Мунипов 8

Правило параллелограмма позволяет определить свойство коммутативности для суммы векторов Для суммы векторов справедливо свойство коммутативности Для суммы векторов справедливо: 13. 12. 2010 Р. Мунипов 9
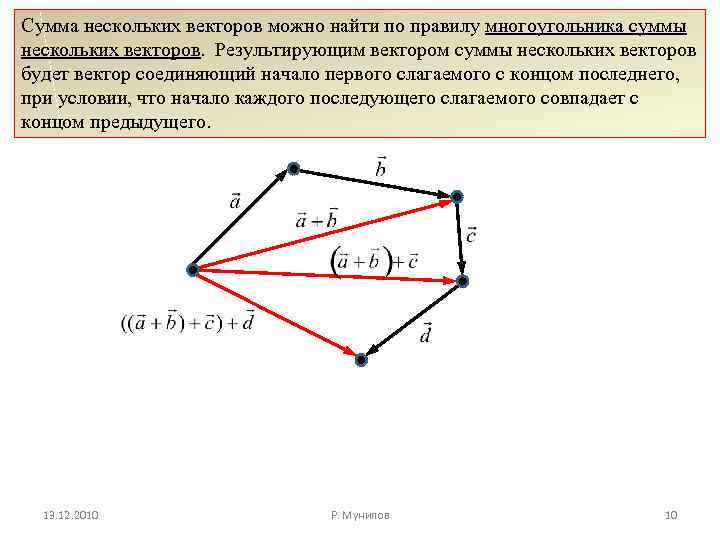
Сумма нескольких векторов можно найти по правилу многоугольника суммы нескольких векторов. Результирующим вектором суммы нескольких векторов будет вектор соединяющий начало первого слагаемого с концом последнего, при условии, что начало каждого последующего слагаемого совпадает с концом предыдущего. 13. 12. 2010 Р. Мунипов 10
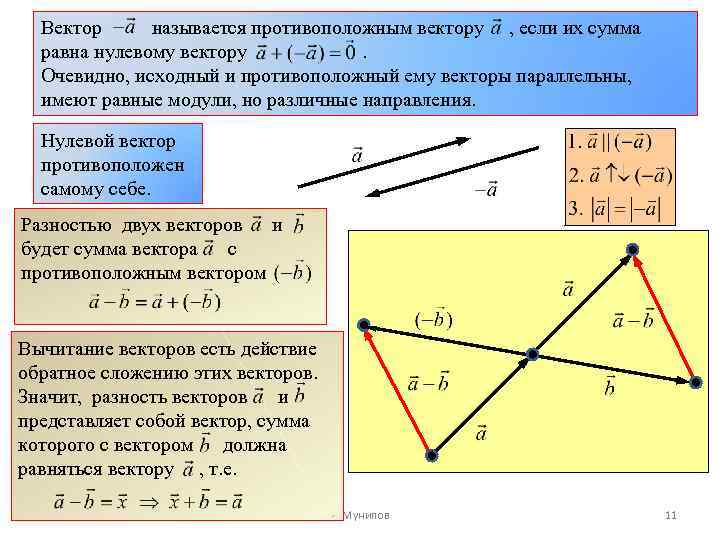
Вектор называется противоположным вектору , если их сумма равна нулевому вектору. Очевидно, исходный и противоположный ему векторы параллельны, имеют равные модули, но различные направления. Нулевой вектор противоположен самому себе. Разностью двух векторов и будет сумма вектора с противоположным вектором Вычитание векторов есть действие обратное сложению этих векторов. Значит, разность векторов и представляет собой вектор, сумма которого с вектором должна равняться вектору , т. е. 13. 12. 2010 Р. Мунипов 11
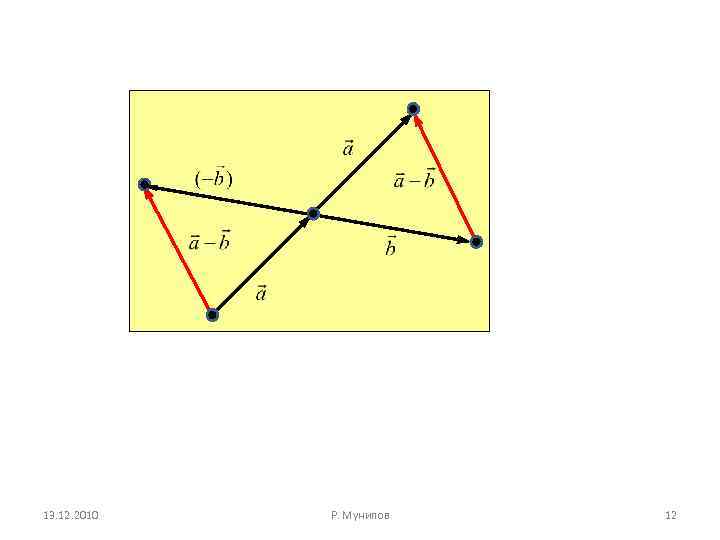
13. 12. 2010 Р. Мунипов 12
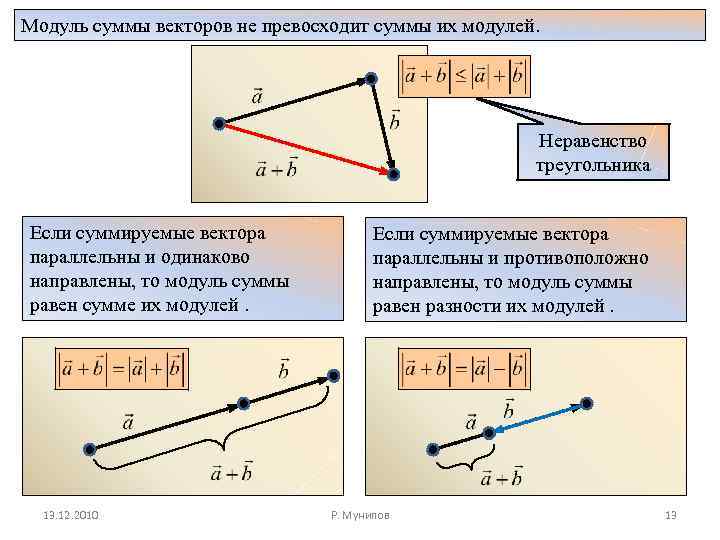
Модуль суммы векторов не превосходит суммы их модулей. Неравенство треугольника Если суммируемые вектора параллельны и одинаково направлены, то модуль суммы равен сумме их модулей. 13. 12. 2010 Если суммируемые вектора параллельны и противоположно направлены, то модуль суммы равен разности их модулей. Р. Мунипов 13
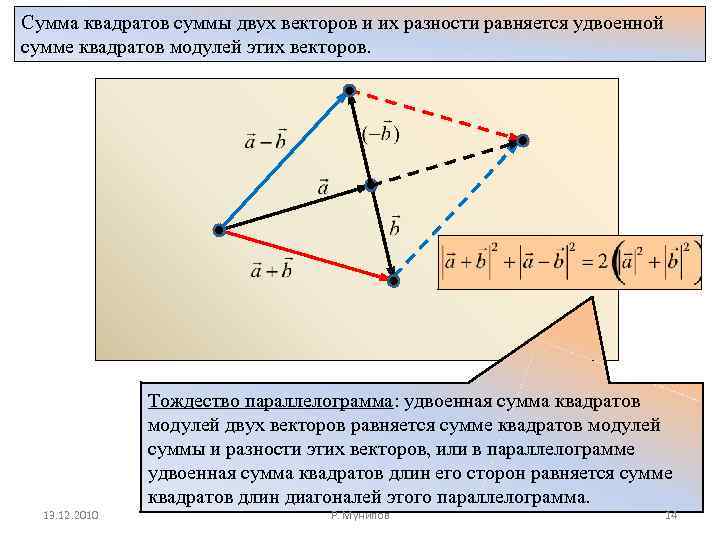
Сумма квадратов суммы двух векторов и их разности равняется удвоенной сумме квадратов модулей этих векторов. Тождество параллелограмма: удвоенная сумма квадратов модулей двух векторов равняется сумме квадратов модулей суммы и разности этих векторов, или в параллелограмме удвоенная сумма квадратов длин его сторон равняется сумме квадратов длин диагоналей этого параллелограмма. 13. 12. 2010 Р. Мунипов 14
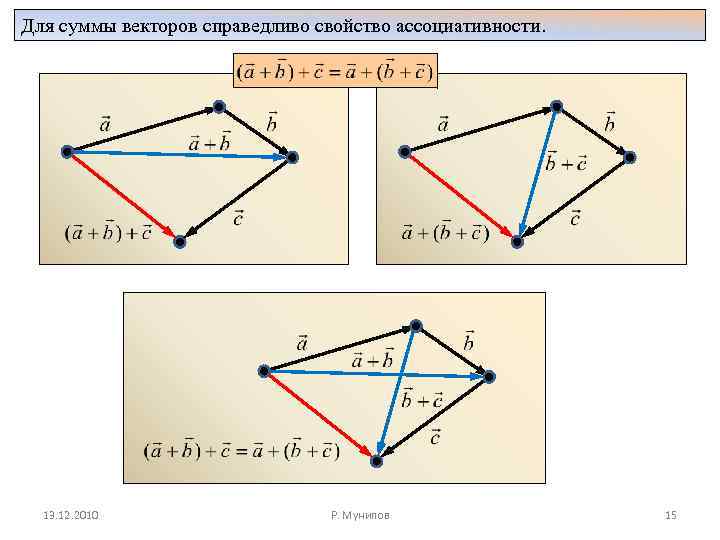
Для суммы векторов справедливо свойство ассоциативности. 13. 12. 2010 Р. Мунипов 15

Произведением вектора на скаляр (число) есть вектор одинаково направленный с перемножаемым вектором, если скаляр положительный, и противоположно направленный с ним, если скаляр отрицателен, модуль произведения равен произведению модуля умножаемого вектора на абсолютное значение скаляра. При умножении вектора на число по модулю большее единице, вектор удлиняется, при умножении на число по модулю меньшее единице вектор укорачивается. 13. 12. 2010 Р. Мунипов 16

Очевидно, а) произведение нулевого вектора на число даст нулевой вектор, б) произведение любого вектора на число нуль даст нулевой вектор, 13. 12. 2010 Р. Мунипов 17

Из определения вектора на число следуют свойства: 1) При умножении на единицу вектор не изменяется: 2) При умножении вектора на число (-1) получается вектор противоположный исходному: 3) Деление вектора на число отличное от нуля есть умножение этого вектора на число обратное исходному: 4) При деление ненулевого вектора на его длину, получаем единичный вектор со направленный с исходным, который называют ортом к исходному вектору: 5) При умножении единичного вектора на число, получаем вектор параллельный исходному, длина которого равна модулю этого числа: 13. 12. 2010 Р. Мунипов 18
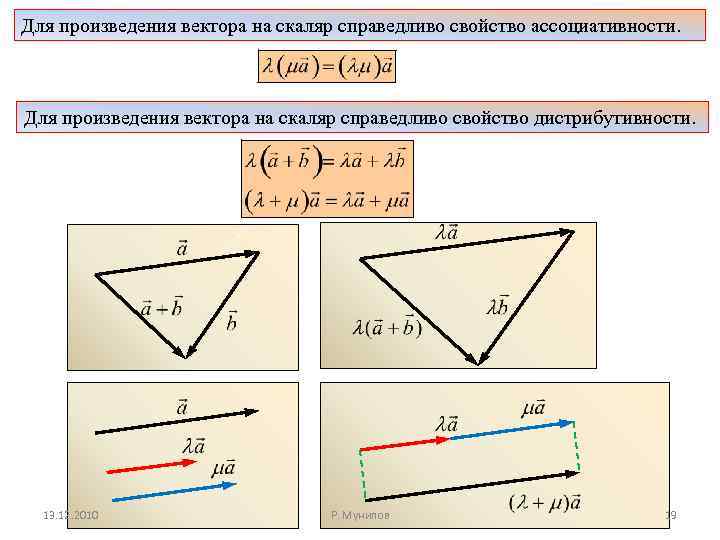
Для произведения вектора на скаляр справедливо свойство ассоциативности. Для произведения вектора на скаляр справедливо свойство дистрибутивности. 13. 12. 2010 Р. Мунипов 19

Сложение векторов и умножение вектора на число называют линейными операциями над векторами Для линейных операций над векторами справедливы свойства: 13. 12. 2010 Р. Мунипов 20
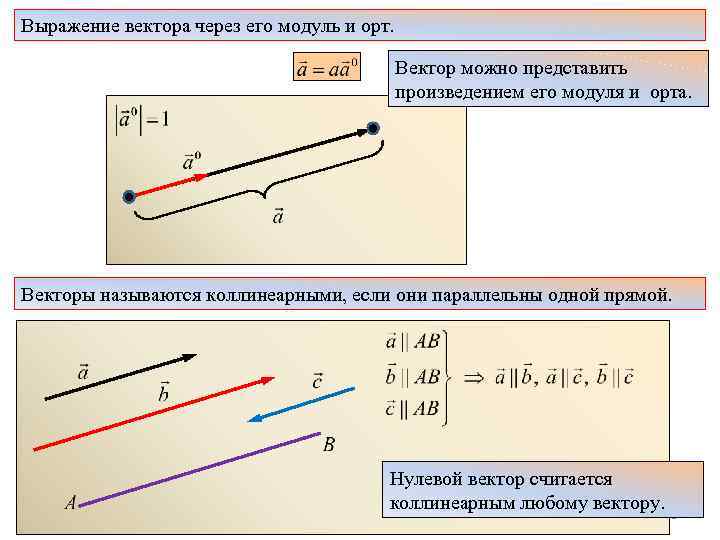
Выражение вектора через его модуль и орт. Вектор можно представить произведением его модуля и орта. Векторы называются коллинеарными, если они параллельны одной прямой. 13. 12. 2010 Р. Мунипов Нулевой вектор считается коллинеарным любому вектору. 21
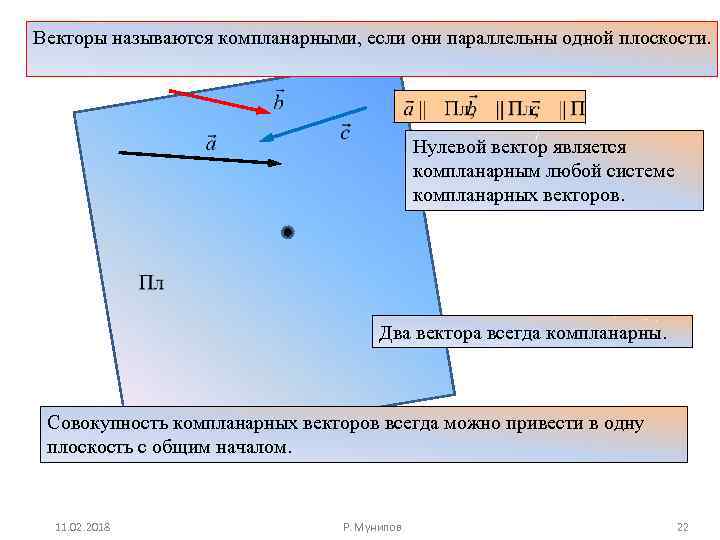
Векторы называются компланарными, если они параллельны одной плоскости. Нулевой вектор является компланарным любой системе компланарных векторов. Два вектора всегда компланарны. Совокупность компланарных векторов всегда можно привести в одну плоскость с общим началом. 11. 02. 2018 Р. Мунипов 22

Вектор называется линейной комбинацией векторов справедливо , если где – некоторые числа. В этом случае говорят, что вектор разложен по векторам , числа называют коэффициентами разложения Линейная комбинация векторов коэффициентов называются нетривиальной, если хотя бы один из отличен от нуля. Линейная комбинация называется тривиальной, если она равна нулевому вектору. 13. 12. 2010 Р. Мунипов 23

Для линейной комбинации векторов справедливы свойства: 1. Если векторы коллинеарны, то любая их линейная комбинация им коллинеарна. 2. Если векторы компланарны, то любая их линейная комбинация им компланарна. Действительно, покажем справедливость первого. При умножении вектора на число получаем (по определению) вектор, коллинеарный данному. При сложении двух векторов, параллельных некоторой прямой, получаем ( по определению) вектор, параллельный этой же прямой. Поэтому линейная комбинация двух векторов и коллинеарна им. По индукции свойство распространяется на любое конечное число коллинеарных векторов. 13. 12. 2010 Р. Мунипов 24

Система векторов существуют такие числа называется линейно зависимой, если , не все равные нулю одновременно, что т. е. существует хотя бы одна нетривиальная линейная комбинация этих векторов, равная нулевому вектору. В противном случае, т. е. если только тривиальная линейная комбинация данных векторов равна нулевому вектору, векторы называются линейно независимыми. Если рассматривать один вектор , как систему, то при , он будет, согласно определения, линейно зависим; если , то вектор линейно независим. Очевидно, нулевой вектор линейно зависим с любым вектором, действительно Значит, всякая совокупность векторов содержащая нулевой вектор линейно 13. 12. 2010 Р. Мунипов 25 зависимая.

СВОЙСТВА ЛИНЕЙНО ЗАВИСИМЫХ И ЛИНЕЙНО НЕЗАВИСИМЫХ ВЕКТОРОВ 1. Если в системе векторов присутствует нулевой вектор, то она линейно зависима. 2. Если в системе векторов присутствуют два равных вектора, то она линейно зависима. 3. Если в системе векторов имеются два пропорциональных вектора , то она линейно зависимая. 4. Система векторов линейно зависимая, тогда и только тогда когда, по крайней мере, один из векторов этой системы будет равен нетривиальной линейной комбинации других векторов этой системы, 5. Любые векторы линейно независимой системы, образуют линейно независимую подсистему. 6. Система векторов, содержащая линейно зависимую подсистему, линейно зависимая. 13. 12. 2010 Р. Мунипов 26

СВОЙСТВА ЛИНЕЙНО ЗАВИСИМЫХ И ЛИНЕЙНО НЕЗАВИСИМЫХ ВЕКТОРОВ (продолжение) 7. Если система векторов линейно независимая, а после присоединения к ней вектора оказывается линейно зависимой, то вектор можно разложить по векторам , и притом единственным образом. Покажем справедливость последнего свойства. Так как система векторов линейно зависимая , то, по определению, существуют числа не все равные нулю, что справедливо. Причём , в самом деле, если коэффициент , то , значит нетривиальная линейная комбинация векторов равна нулевому вектору, это противоречит условию их линейной независимости. Итак, справедливо равенство , и тогда т. е. вектор 13. 12. 2010 есть линейная комбинация векторов Р. Мунипов . 27

Покажем справедливость последнего свойства (продолжение). Справедливость единственности разложения вектора по векторам линейно независимой системы докажем от противного. Пусть имеются два разложения и , причём не все соответствующие коэффициенты разложений равны между собой, например, не ограничивая общности, . Тогда из равенства получаем Следовательно, нетривиальная линейная комбинация векторов равна нулевому вектору, что противоречит условию линейной независимости этих векторов. Полученное противоречие подтверждает единственность разложения. 13. 12. 2010 Р. Мунипов 28

Из свойств линейно зависимой и независимой системы векторов следует, что если среди векторов существует линейно зависимая подсистема векторов, то вся исходная система векторов будет линейно зависимой, И, если система векторов линейно независимая, то и всякая её подсистема векторов также будет линейно независимой. Если среди векторов системы, хотя бы один из них является нетривиальной линейной комбинацией других векторов, то вся система будет линейно зависимой. Если система векторов линейно зависимая, а её подсистема векторов линейно независимая, то вектор будет равен линейной комбинации векторов 13. 12. 2010 Р. Мунипов 29

Векторы называются линейно зависимыми, если справедливо где скалярные коэффициенты не все равны нулю. Между векторами имеет место линейная зависимость Векторы называются линейно независимыми, если равенство выполнятся тогда и только тогда, когда все скалярные коэффициенты равны нулю. 13. 12. 2010 Р. Мунипов 30
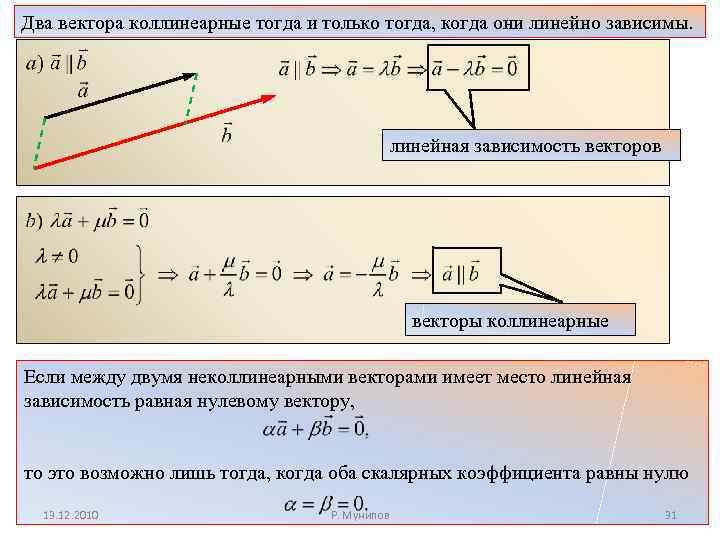
Два вектора коллинеарные тогда и только тогда, когда они линейно зависимы. линейная зависимость векторов векторы коллинеарные Если между двумя неколлинеарными векторами имеет место линейная зависимость равная нулевому вектору, то это возможно лишь тогда, когда оба скалярных коэффициента равны нулю 13. 12. 2010 Р. Мунипов 31

Три вектора компланарные тогда и только тогда, когда они линейно зависимы. линейная зависимость векторов Если между тремя некомпланарными векторами имеет место линейная векторы образуют треугольник зависимость значит компланарные то это возможно лишь тогда, когда все скалярных коэффициента равны нулю 13. 12. 2010 Р. Мунипов 32
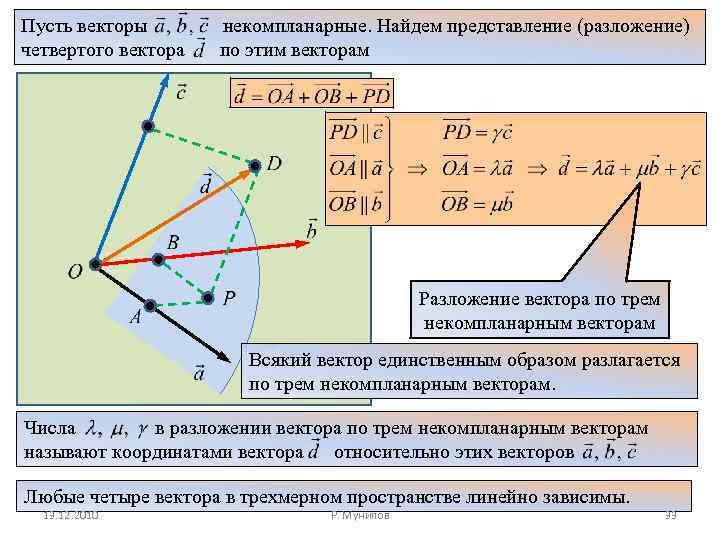
Пусть векторы четвертого вектора некомпланарные. Найдем представление (разложение) по этим векторам Разложение вектора по трем некомпланарным векторам Всякий вектор единственным образом разлагается по трем некомпланарным векторам. Числа в разложении вектора по трем некомпланарным векторам называют координатами вектора относительно этих векторов Любые четыре вектора в трехмерном пространстве линейно зависимы. 13. 12. 2010 Р. Мунипов 33
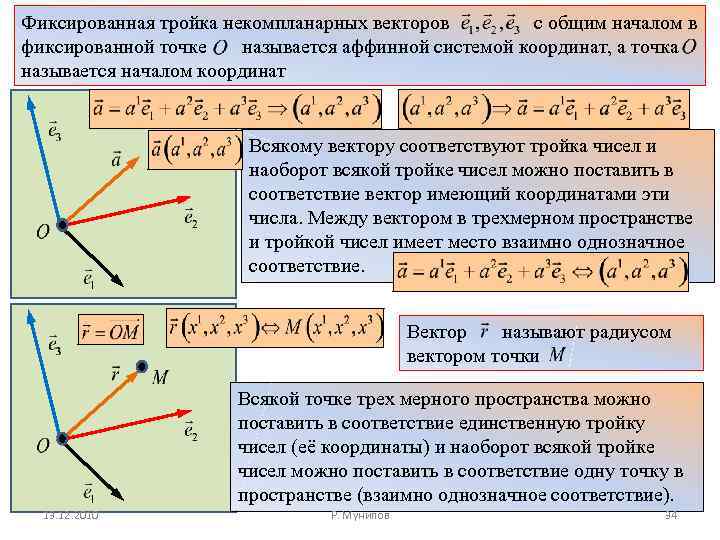
Фиксированная тройка некомпланарных векторов с общим началом в фиксированной точке называется аффинной системой координат, а точка называется началом координат Всякому вектору соответствуют тройка чисел и наоборот всякой тройке чисел можно поставить в соответствие вектор имеющий координатами эти числа. Между вектором в трехмерном пространстве и тройкой чисел имеет место взаимно однозначное соответствие. Вектор называют радиусом вектором точки Всякой точке трех мерного пространства можно поставить в соответствие единственную тройку чисел (её координаты) и наоборот всякой тройке чисел можно поставить в соответствие одну точку в пространстве (взаимно однозначное соответствие). 13. 12. 2010 Р. Мунипов 34
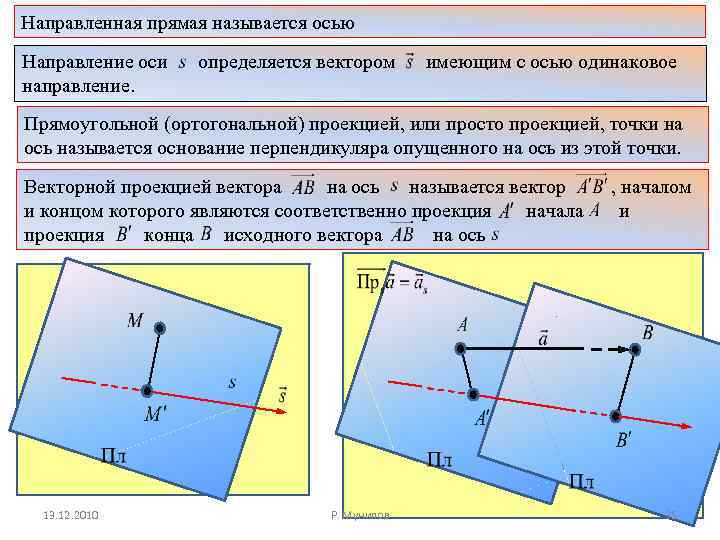
Направленная прямая называется осью Направление оси направление. определяется вектором имеющим с осью одинаковое Прямоугольной (ортогональной) проекцией, или просто проекцией, точки на ось называется основание перпендикуляра опущенного на ось из этой точки. Векторной проекцией вектора на ось называется вектор и концом которого являются соответственно проекция начала проекция конца исходного вектора на ось 13. 12. 2010 Р. Мунипов , началом и 35
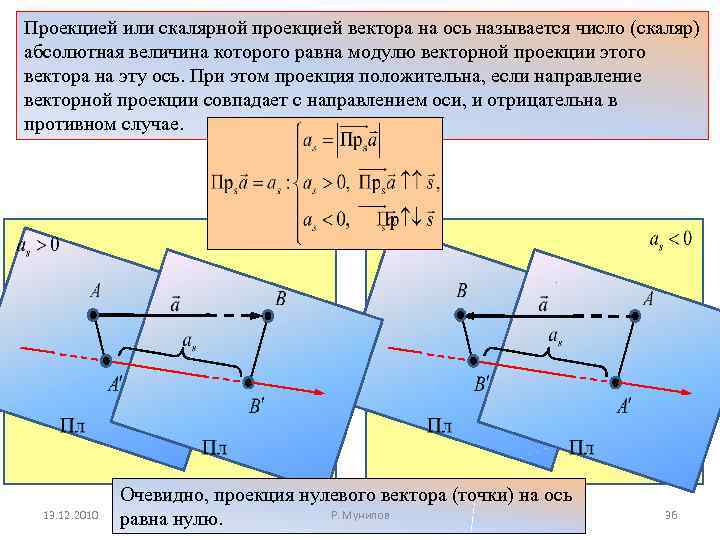
Проекцией или скалярной проекцией вектора на ось называется число (скаляр) абсолютная величина которого равна модулю векторной проекции этого вектора на эту ось. При этом проекция положительна, если направление векторной проекции совпадает с направлением оси, и отрицательна в противном случае. 13. 12. 2010 Очевидно, проекция нулевого вектора (точки) на ось Р. Мунипов равна нулю. 36
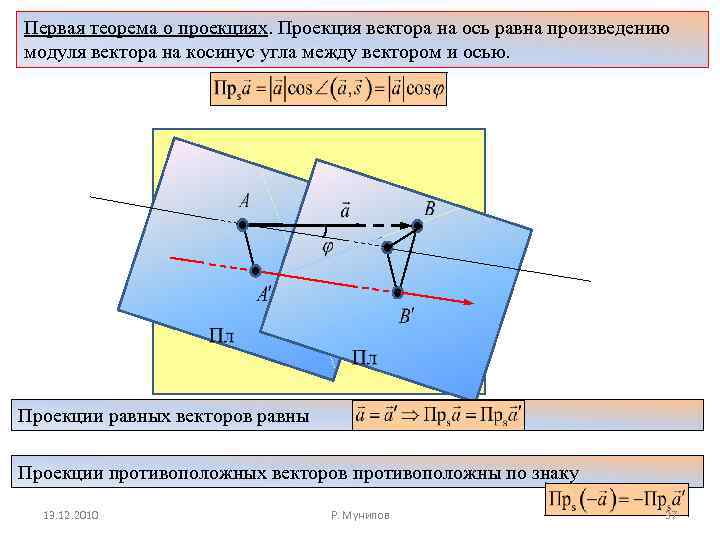
Первая теорема о проекциях. Проекция вектора на ось равна произведению модуля вектора на косинус угла между вектором и осью. Проекции равных векторов равны Проекции противоположных векторов противоположны по знаку 13. 12. 2010 Р. Мунипов 37

Вторая теорема о проекциях. Проекция суммы векторов равна сумме проекций. Третья теорема о проекциях. Проекция произведения вектора на число равна произведению этого числа на проекцию этого вектора. Проекция линейной комбинации векторов равна той же линейной комбинации проекций этих векторов. 13. 12. 2010 Р. Мунипов 38
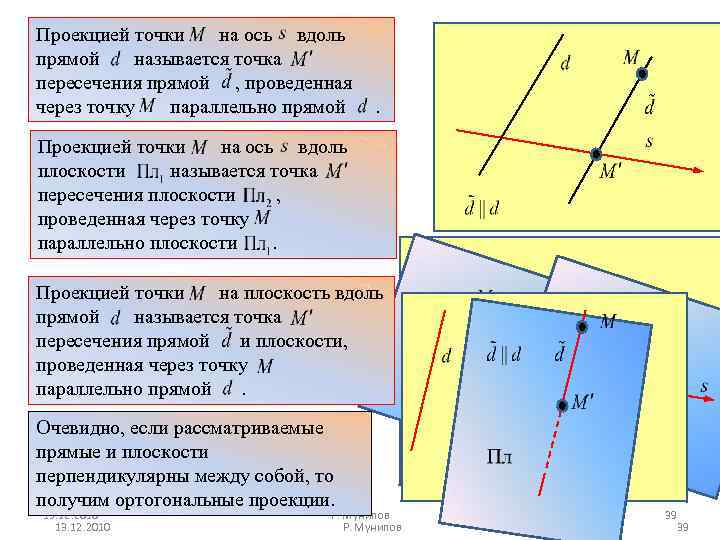
Проекцией точки на ось вдоль прямой называется точка пересечения прямой , проведенная через точку параллельно прямой . Проекцией точки на ось вдоль плоскости называется точка пересечения плоскости , проведенная через точку параллельно плоскости. Проекцией точки на плоскость вдоль прямой называется точка пересечения прямой и плоскости, проведенная через точку параллельно прямой. Очевидно, если рассматриваемые прямые и плоскости перпендикулярны между собой, то получим ортогональные проекции. 13. 12. 2010 Р. Мунипов 39 39

Для проекции вектора справедливо: 1. Если на плоскости заданы две пересекающиеся прямые и , то любой вектор на этой плоскости можно однозначно представить в виде суммы своих векторных проекций и вдоль этих прямых 2. Если пространстве заданы три прямые и пересекающиеся в одной точке и не лежащие на одной прямой, то любой вектор в пространстве можно однозначно представить в виде суммы своих векторных проекций вдоль этих прямых 13. 12. 2010 Р. Мунипов

Справедливо обратное: 1. Если вектор на плоскости равен сумме двух некомпланарных векторов, , то эти векторы и являются векторными проекциями исходного вектора вдоль прямых определяемых этими векторами соответственно. 2. Если вектор в пространстве равен сумме трёх некомпланарных векторов, то эти векторы являются векторными проекциями исходного вектора вдоль прямых определяемых этими векторами соответственно. 13. 12. 2010 Р. Мунипов

Пусть в плоскости два единичных вектора неколлинеарные между собой, тогда любой вектор в этой плоскости есть линейная комбинация этих единичных векторов с коэффициентами равными алгебраическим значениям проекций этого вектора на оси, определяемые единичными векторами (проекция на каждую ось рассматривается вдоль другой оси). 13. 12. 2010 Р. Мунипов 42
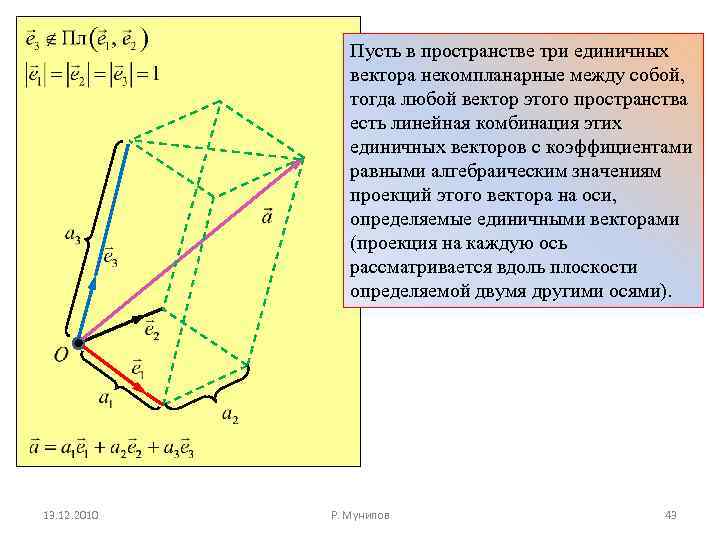
Пусть в пространстве три единичных вектора некомпланарные между собой, тогда любой вектор этого пространства есть линейная комбинация этих единичных векторов с коэффициентами равными алгебраическим значениям проекций этого вектора на оси, определяемые единичными векторами (проекция на каждую ось рассматривается вдоль плоскости определяемой двумя другими осями). 13. 12. 2010 Р. Мунипов 43

Любая пара неколлинеарных единичных векторов на плоскости и любые три неколлинеарных единичных векторов в пространстве, заданных в определенном порядке, называются базисом множества (или многообразия) всех векторов, лежащих в этой плоскости или пространстве соответственно. Сами эти единичные векторы называют базисными, а линейное представление вектора по этим базисным векторам называется разложением вектора по базису. Коэффициенты в разложении определяются однозначно как алгебраические значения проекции вектора на оси, определяемые базисными векторами, и называются координатами вектора относительно этого и только этого базиса. Линейное разложение вектора по базисам в плоскости и пространстве 13. 12. 2010 Координаты вектора по базисам в плоскости и пространстве Р. Мунипов Очевидно, два вектора равны если равны их соответствующие координаты относительно некоторых базисных векторов. 44
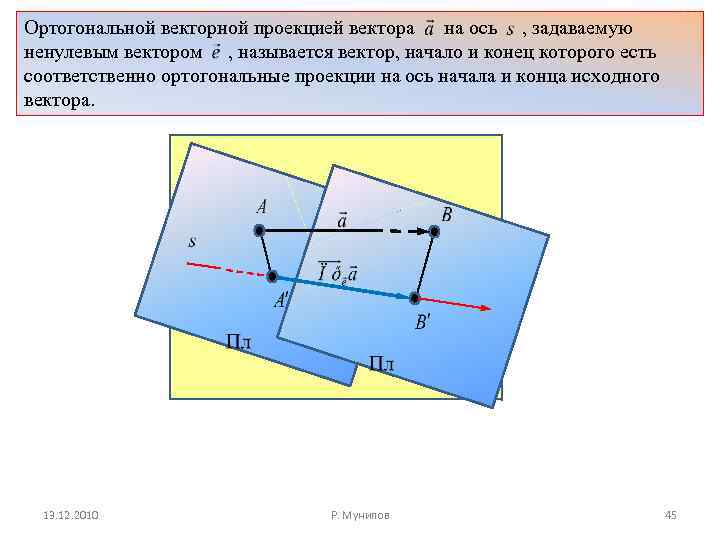
Ортогональной векторной проекцией вектора на ось , задаваемую ненулевым вектором , называется вектор, начало и конец которого есть соответственно ортогональные проекции на ось начала и конца исходного вектора. 13. 12. 2010 Р. Мунипов 45

Ортогональной векторной проекцией вектора на прямую , называется вектор, начало и конец которого есть соответственно ортогональные проекции на эту прямую начала и конца исходного вектора. 13. 12. 2010 Р. Мунипов 46
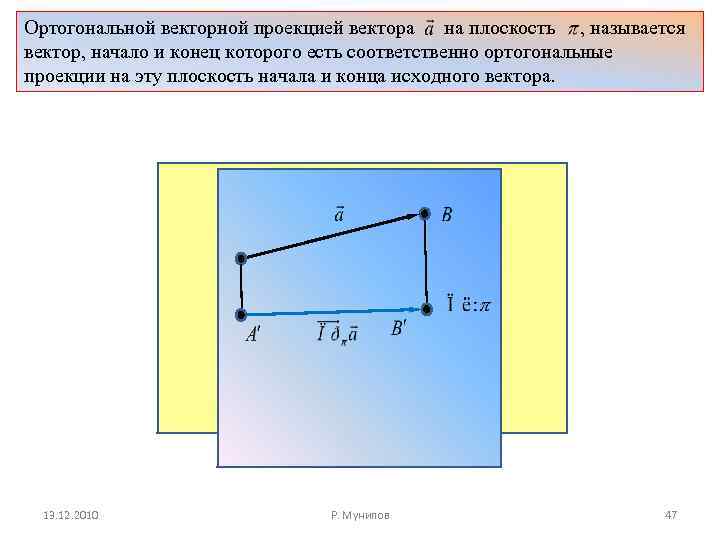
Ортогональной векторной проекцией вектора на плоскость , называется вектор, начало и конец которого есть соответственно ортогональные проекции на эту плоскость начала и конца исходного вектора. 13. 12. 2010 Р. Мунипов 47

Разность между вектором и его ортогональной векторной проекцией называют ортогональной составляющей. Можно рассмотреть соответственно ортогональные составляющие вектора относительно оси, прямой и плоскости, тогда, 13. 12. 2010 Р. Мунипов 48
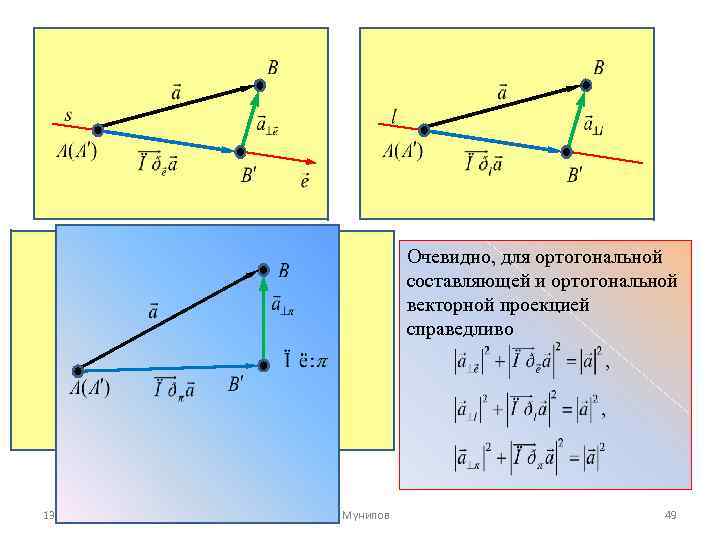
Очевидно, для ортогональной составляющей и ортогональной векторной проекцией справедливо 13. 12. 2010 Р. Мунипов 49

Для ортогональных проекций вектора на прямую справедливо: 1. Если на плоскости заданы две взаимно перпендикулярные прямые и , то любой вектор можно однозначно представить в виде суммы его ортогональных векторных проекций на эти прямые, 2. Если в пространстве заданы три попарно перпендикулярные прямые и , пересекающиеся в одной точке, то любой вектор в пространстве можно однозначно представить в виде суммы его ортогональных векторных проекций на эти прямые, 3. Квадрат длины вектора на плоскости или в пространстве равен сумме квадратов длин его ортогональных векторных проекций, 13. 12. 2010 Р. Мунипов 50

Алгебраическим значением длины ортогональной векторной проекцией вектора на ось задаваемой ненулевым вектором называется длина этой векторной проекции, взятая со знаком плюс, если угол между исходным вектором и вектором , определяющим ось, не превосходит , и с отрицательным знаком, если угол больше , т. е. тогда, 13. 12. 2010 Р. Мунипов 51
Вектор1.pptx