Векторная алгебра Пушникова Марина Юрьевна Определение

Векторная алгебра Пушникова Марина Юрьевна

Определение ► Вектор – это направленный отрезок ► Любой вектор задается длиной (модулем) и направлением ► Обозначение: или где А – начало вектора, В – конец вектора, – длина вектора

Классификация векторов Нулевой вектор – это вектор, длина которого равна нулю Единичный вектор – это вектор, длина которого равна единице ► Равные векторы – это два вектора, у которых совпадают длина и направление ► Противоположные векторы – это два вектора, у которых длины равны, а направления – противоположные ► Коллинеарные векторы – это два вектора, которые лежат на одной прямой или на параллельных прямых ► Сонаправленные векторы – это два коллинеарных вектора с одинаковым направлением ► Противоположно направленные векторы– это два коллинеарных вектора с противоположным направлением ► Компланарные векторы – это три вектора, которые лежат в одной плоскости или на параллельных плоскостях ► ►

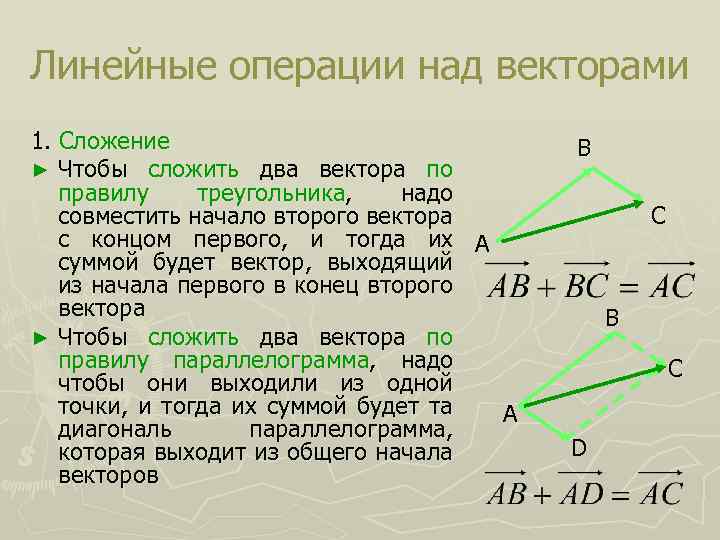
Линейные операции над векторами 1. Сложение ► Чтобы сложить два вектора по правилу треугольника, надо совместить начало второго вектора с концом первого, и тогда их А суммой будет вектор, выходящий из начала первого в конец второго вектора ► Чтобы сложить два вектора по правилу параллелограмма, надо чтобы они выходили из одной точки, и тогда их суммой будет та А диагональ параллелограмма, которая выходит из общего начала векторов В С D

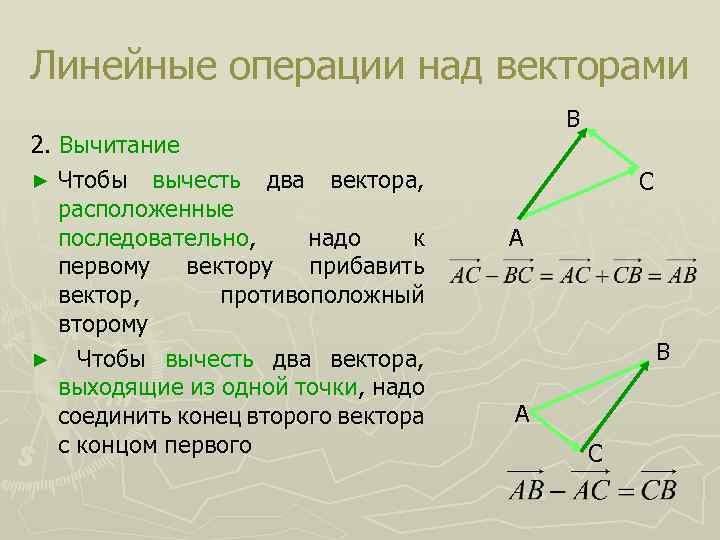
Линейные операции над векторами 2. Вычитание ► Чтобы вычесть два вектора, расположенные последовательно, надо к первому вектору прибавить вектор, противоположный второму ► Чтобы вычесть два вектора, выходящие из одной точки, надо соединить конец второго вектора с концом первого В С А В А С

Линейные операции над векторами 3. Умножение вектора на число ► При умножении вектора на число его длина изменяется в это число раз, а направление остается прежним, если число положительное, и меняется на противоположное, если число отрицательное

Свойства линейных операций ► Переместительное ► Сочетательные ► Распределительные

Прямоугольная система координат на плоскости – это две взаимно перпендикулярные прямые с выбранным направлением и началом отсчета, при этом горизонтальная прямая называется осью абсцисс, а вертикальная – осью ординат ► На осях введем единичные векторы (орты): на оси абсцисс – вектор , а на оси ординат – вектор ► Каждой точке в прямоугольной системе координат поставим в соответствие два числа: абсциссу и ординату ► Абсцисса точки на плоскости – это расстояние от точки до оси ординат ► Ордината точки на плоскости – это расстояние от точки до оси абсцисс ►

Прямоугольная система координат в пространстве ► ► ► Прямоугольная система координат в пространстве – это три взаимно перпендикулярные прямые с выбранным направлением и началом отсчета, при этом горизонтальная прямая, направленная на нас, называется осью абсцисс, горизонтальная прямая, направленная вправо от нас - осью ординат, а вертикальная прямая, направленная вверх – осью аппликат На осях введем единичные векторы (орты): на оси абсцисс – вектор на оси ординат – вектор , а на оси аппликат вектор Каждой точке в прямоугольной системе координат поставим в соответствие три числа: абсциссу, ординату и аппликату Абсцисса точки в пространстве – это расстояние от точки до плоскости OYZ Ордината точки в пространстве – это расстояние от точки до плоскости OXZ Аппликата точки пространстве– это расстояние от точки до плоскости OXY

Теоремы о разложении вектора ► Любой вектор на плоскости можно разложить в линейную комбинацию двух неколлинеарных векторов и при том только единственным образом Например: ► Любой вектор в пространстве можно разложить в линейную комбинацию трех некомпланарных векторов и при том только единственным образом Например:

Координаты вектора – это числа, стоящие перед ортами в разложении вектора по ортам ► Координаты вектора – это координаты конца вектора, выходящего из начала координат ► Чтобы найти координаты вектора, надо из У координат конца вычесть у2 у1 координаты начала ► У у А(х; у) О х В(х2; у2) А(х1; у1) О х1 х2 Х Х

Действия над векторами в координатной форме ► ► ► Чтобы сложить или вычесть два вектора в координатной форме, надо соответствующие координаты сложить или вычесть Чтобы умножить вектор в координатной форме на число, надо каждую координату умножить на это число Векторы равны тогда и только тогда, когда равны соответствующие координаты Вектора коллинеарны тогда и только тогда, когда их координаты пропорциональны Длина вектора в координатной форме равна квадратному корню из суммы квадратов его координат

Скалярное произведение векторов ► Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними ► Обозначение: или

Скалярное произведение векторов в координатной форме Скалярное произведение двух векторов, заданных в координатной форме равно сумме произведений соответствующих координат Доказательство:

Свойства скалярного произведения векторов 1. 2. 3. 4. 5. 6. Переместительное Сочетательное Распределительное Скалярный квадрат вектора равен квадрату его длины Два вектора перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю Косинус угла между векторами равен скалярному произведению этих векторов, деленному на произведение длин этих векторов

Пример Найти косинус угла BAD тетраэдра ABCD, если А(-5; 1; 1), В(1; -2), С(1; -3), D(-1; -4; -1)

Векторное произведение векторов ► 1. 2. 3. ► ► Векторным произведением двух векторов называется вектор, который перпендикулярен двум данным образует с ними правую тройку с длиной, равной произведению длин данных векторов на синус угла между ними Обозначение: или Следствия:

Векторное произведение векторов заданных в координатной форме Векторное произведение двух векторов заданных в координатной форме равно определителю третьего порядка, в первой строке которого стоят орты, во второй строке стоят координаты первого вектора, а в третьей строке – координаты второго вектора Доказательство:

Свойства векторного произведения векторов 1. 2. 3. 4. 5. 6. Антипереместительное Сочетательное Распределительное Векторный квадрат вектора равен нулю Векторное произведение двух коллинеарных векторов равно нулю Модуль векторного произведения равен площади параллелограмма, а половина модуля векторного произведения равна площади треугольника

Пример Найти площадь грани ABD тетраэдра ABCD, если А(-5; 1; 1), В(1; -2), С(1; -3), D(-1; -4; -1)

Определение смешанного произведения векторов ► Смешанным произведением трех векторов называется скалярное произведение векторного произведения двух первых векторов на третий вектор ► Обозначение:

Свойства смешанного произведения векторов 1. 2. 3. 4. 5. 6. Переместительные Смешанное произведение трех компланарных векторов равно нулю Смешанное произведение векторов в координатной форме равно определителю третьего порядка, в строках которого записаны координаты соответствующих векторов Модуль смешанного произведения векторов равен объему параллелепипеда, построенного на этих векторах Объем тетраэдра равен модулю смешанного произведения векторов деленному на 6 Если смешанное произведение векторов положительно, то эти вектора образуют правую тройку. Если смешанное произведение векторов отрицательно, то эти вектора образуют левую тройку c b a c

Пример Вычислить объем тетраэдра ABCD, если А(-5; 1; 1), В(1; -2), С(1; -3), D(-1; -4; -1)