Вектор2.pptx
- Количество слайдов: 55

Векторная алгебра
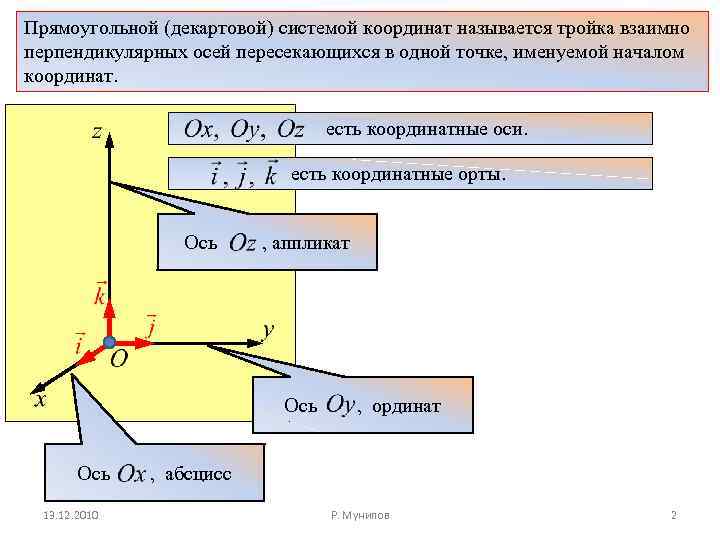
Прямоугольной (декартовой) системой координат называется тройка взаимно перпендикулярных осей пересекающихся в одной точке, именуемой началом координат. есть координатные оси. есть координатные орты. Ось , аппликат Ось 13. 12. 2010 , ординат , абсцисс Р. Мунипов 2
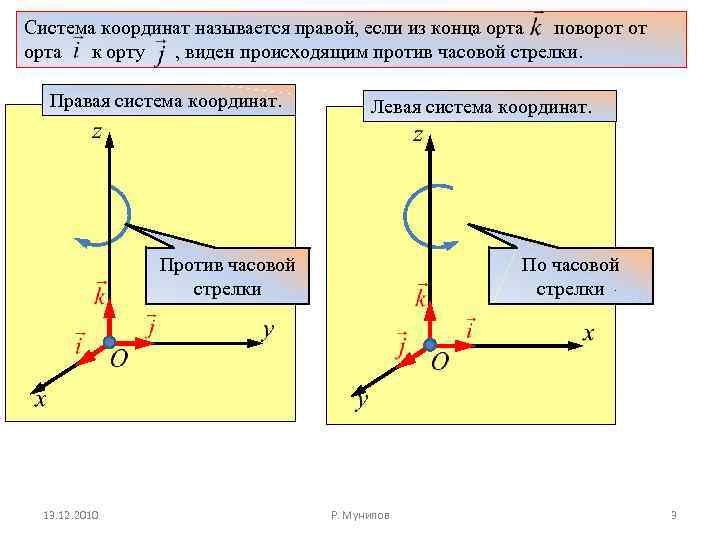
Система координат называется правой, если из конца орта поворот от орта к орту , виден происходящим против часовой стрелки. Правая система координат. Левая система координат. Против часовой стрелки 13. 12. 2010 По часовой стрелки Р. Мунипов 3
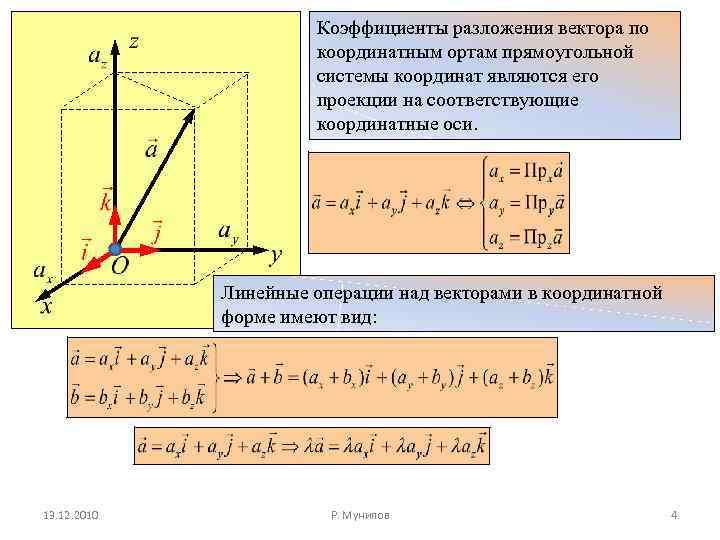
Коэффициенты разложения вектора по координатным ортам прямоугольной системы координат являются его проекции на соответствующие координатные оси. Линейные операции над векторами в координатной форме имеют вид: 13. 12. 2010 Р. Мунипов 4
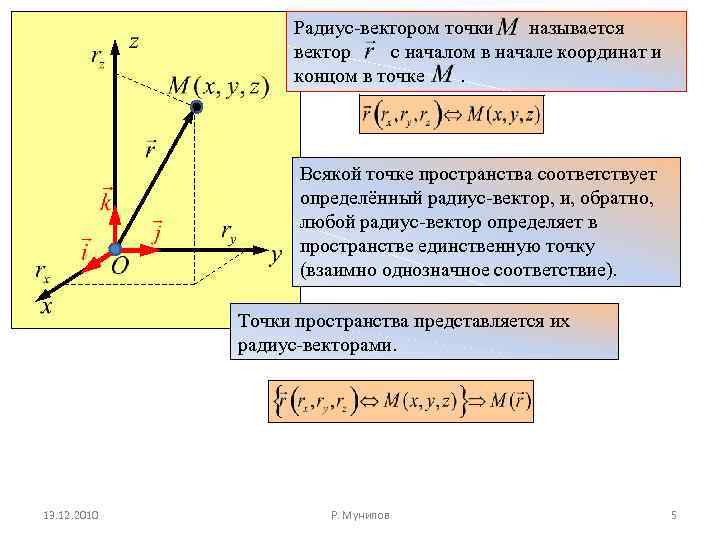
Радиус-вектором точки называется вектор с началом в начале координат и концом в точке. Всякой точке пространства соответствует определённый радиус-вектор, и, обратно, любой радиус-вектор определяет в пространстве единственную точку (взаимно однозначное соответствие). Точки пространства представляется их радиус-векторами. 13. 12. 2010 Р. Мунипов 5
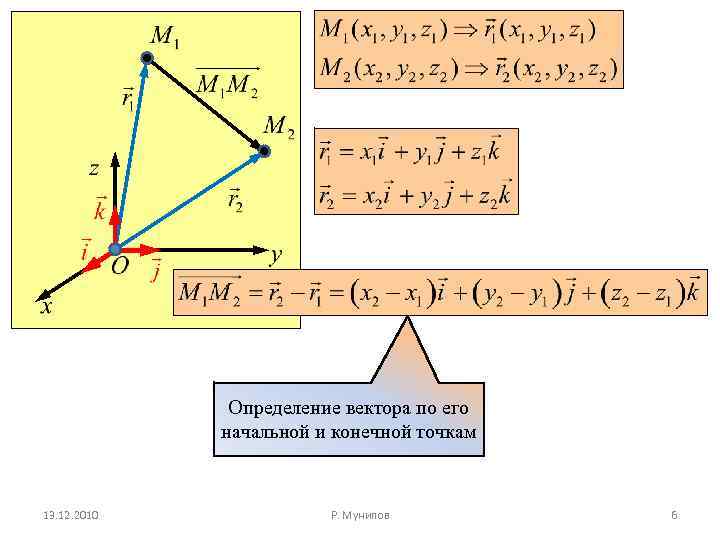
Определение вектора по его начальной и конечной точкам 13. 12. 2010 Р. Мунипов 6
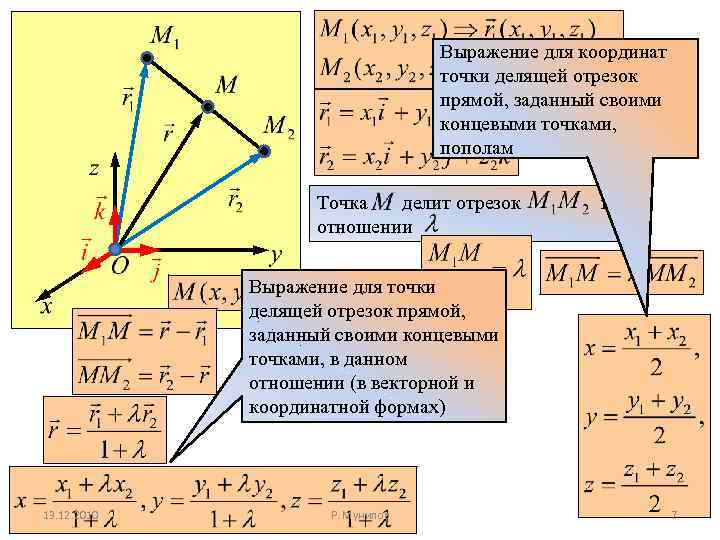
Выражение для координат точки делящей отрезок прямой, заданный своими концевыми точками, пополам Точка делит отрезок отношении в Выражение для точки делящей отрезок прямой, заданный своими концевыми точками, в данном отношении (в векторной и координатной формах) 13. 12. 2010 Р. Мунипов 7
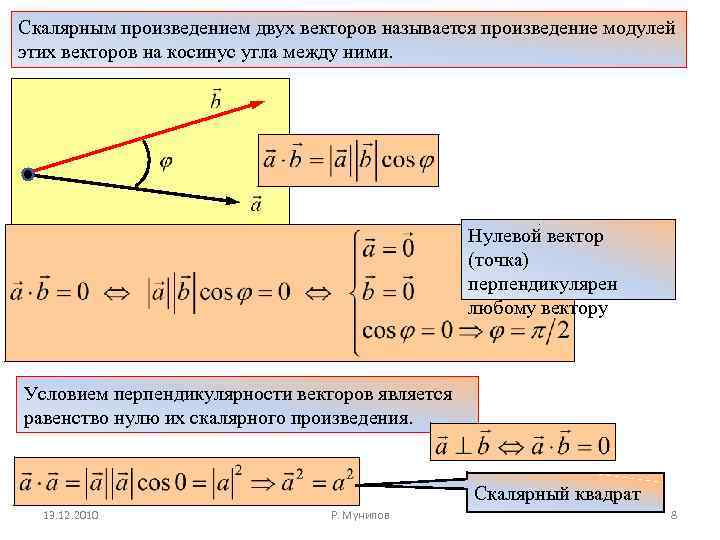
Скалярным произведением двух векторов называется произведение модулей этих векторов на косинус угла между ними. Нулевой вектор (точка) перпендикулярен любому вектору Условием перпендикулярности векторов является равенство нулю их скалярного произведения. Скалярный квадрат 13. 12. 2010 Р. Мунипов 8
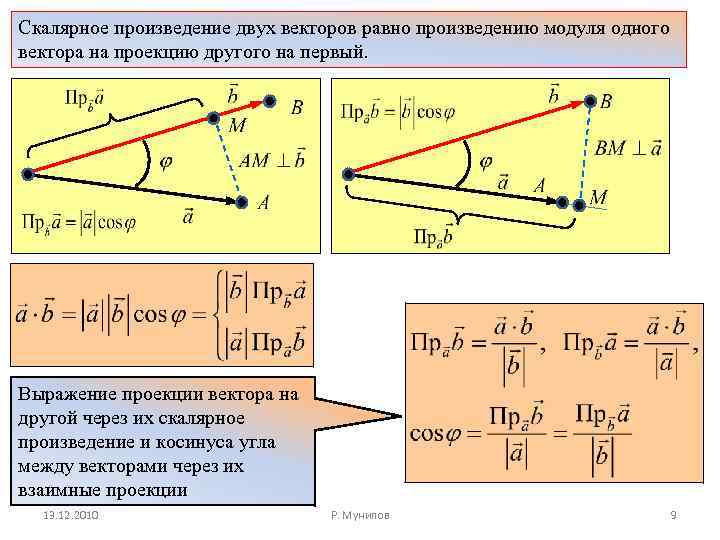
Скалярное произведение двух векторов равно произведению модуля одного вектора на проекцию другого на первый. Выражение проекции вектора на другой через их скалярное произведение и косинуса угла между векторами через их взаимные проекции 13. 12. 2010 Р. Мунипов 9
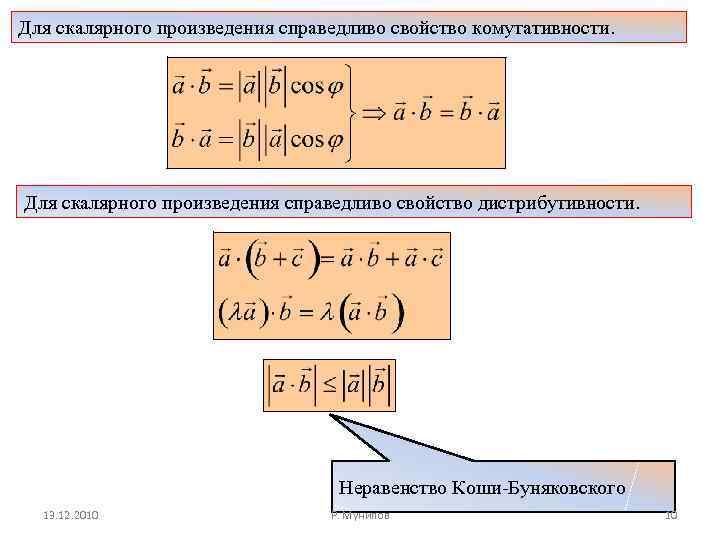
Для скалярного произведения справедливо свойство комутативности. Для скалярного произведения справедливо свойство дистрибутивности. Неравенство Коши-Буняковского 13. 12. 2010 Р. Мунипов 10
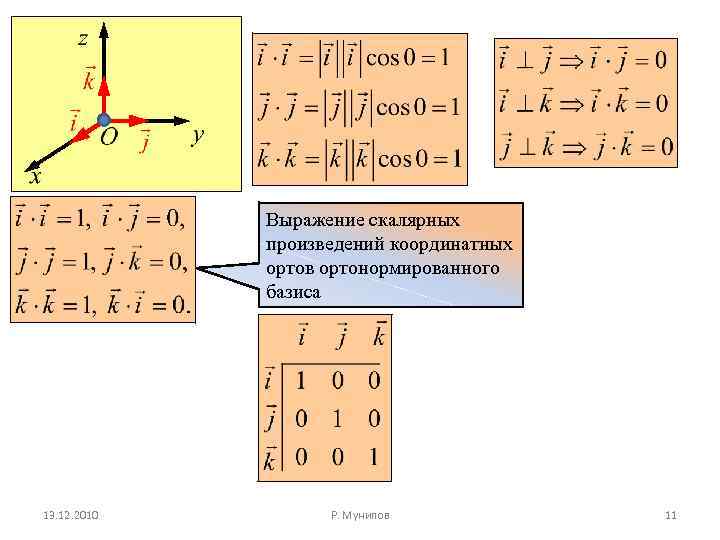
Выражение скалярных произведений координатных ортов ортонормированного базиса 13. 12. 2010 Р. Мунипов 11
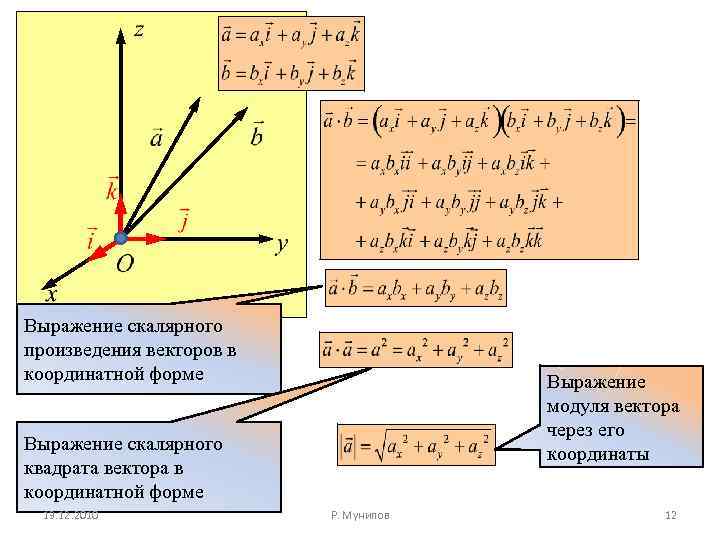
Выражение скалярного произведения векторов в координатной форме Выражение модуля вектора через его координаты Выражение скалярного квадрата вектора в координатной форме 13. 12. 2010 Р. Мунипов 12
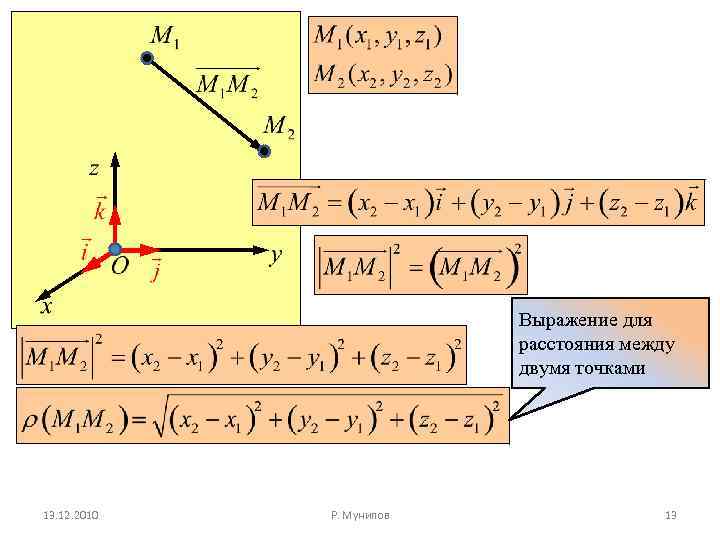
Выражение для расстояния между двумя точками 13. 12. 2010 Р. Мунипов 13
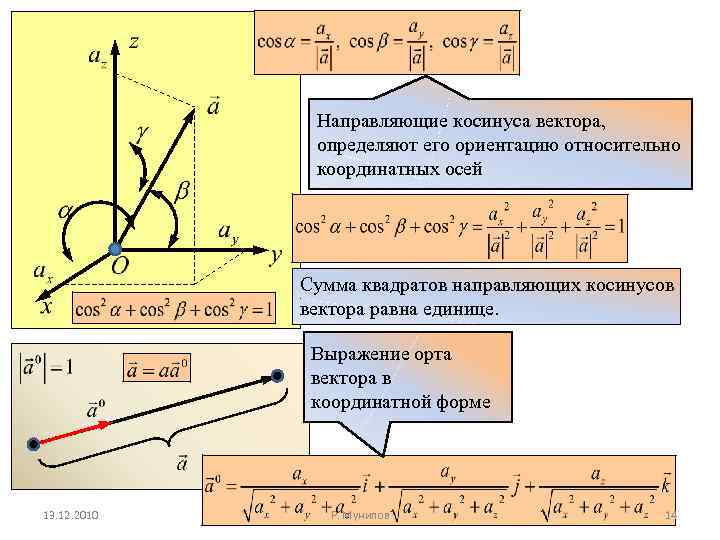
Направляющие косинуса вектора, определяют его ориентацию относительно координатных осей Сумма квадратов направляющих косинусов вектора равна единице. Выражение орта вектора в координатной форме 13. 12. 2010 Р. Мунипов 14

Условие перпендикулярности векторов в координатной форме: сумма произведений одноименных компонент векторов равна нулю Выражение проекции вектора на вектор в координатной форме 13. 12. 2010 Р. Мунипов 15
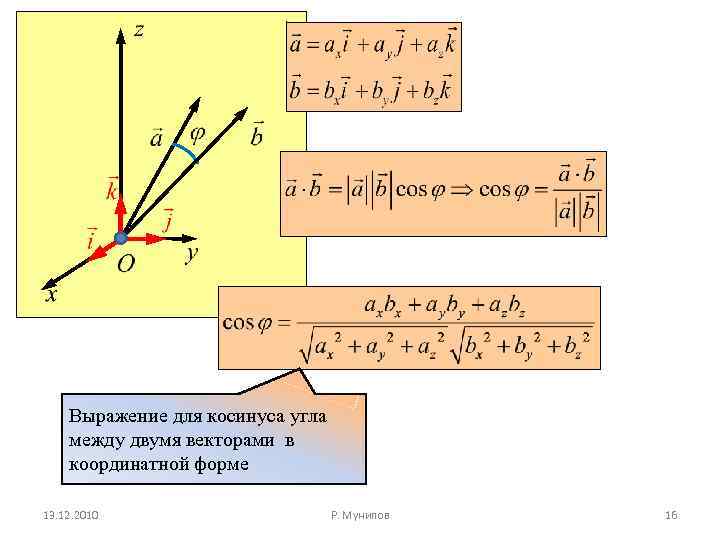
Выражение для косинуса угла между двумя векторами в координатной форме 13. 12. 2010 Р. Мунипов 16
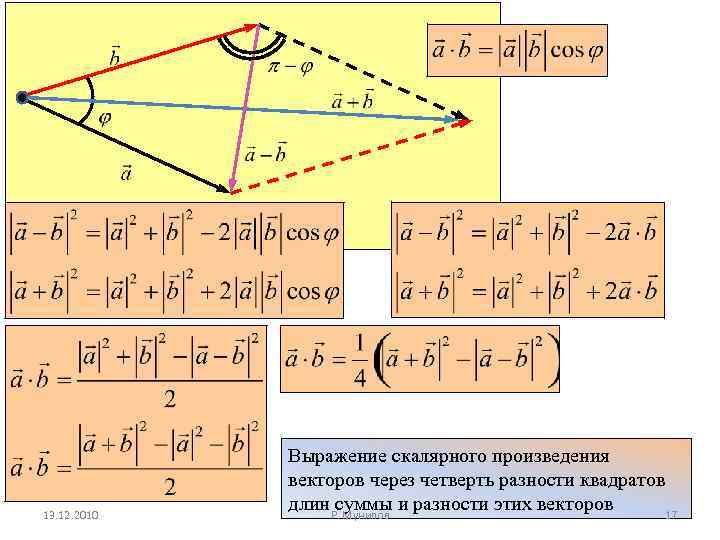
13. 12. 2010 Выражение скалярного произведения векторов через четверть разности квадратов длин. Р. Мунипов и разности этих векторов суммы 17
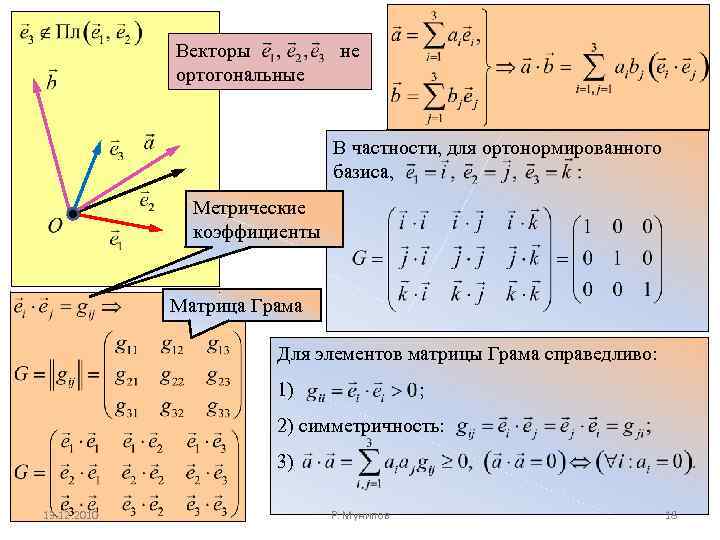
Векторы ортогональные не В частности, для ортонормированного базиса, Метрические коэффициенты Матрица Грама Для элементов матрицы Грама справедливо: 1) ; 2) симметричность: 3) 13. 12. 2010 Р. Мунипов 18

В частности, в двухмерном пространстве и трехмерном Условие базисности системы двух векторов есть отсутствия действительных корней квадратного уравнения 13. 12. 2010 Р. Мунипов 19

Чтобы числа определяли скалярное произведение векторов, необходимо и достаточно, чтобы матрица имела положительные главные миноры, Для того, чтобы система векторов была линейно зависимой необходимо и достаточно, чтобы определитель матрицы Грама равнялся нулю, 13. 12. 2010 Р. Мунипов 20
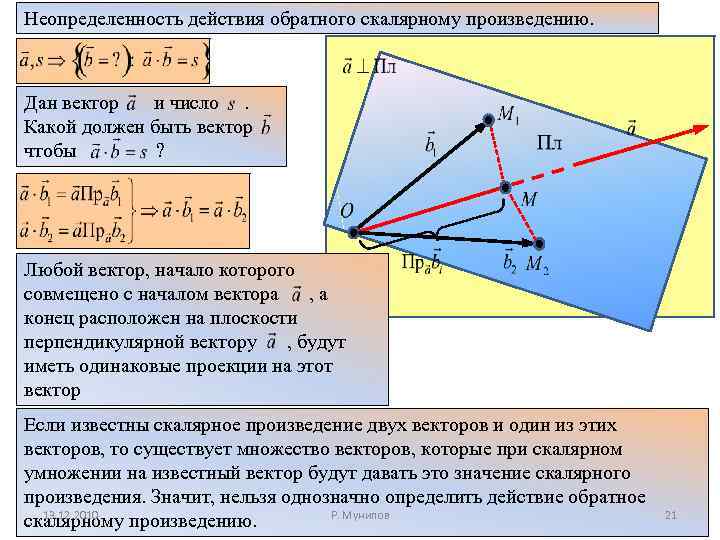
Неопределенность действия обратного скалярному произведению. Дан вектор и число. Какой должен быть вектор чтобы ? Любой вектор, начало которого совмещено с началом вектора , а конец расположен на плоскости перпендикулярной вектору , будут иметь одинаковые проекции на этот вектор Если известны скалярное произведение двух векторов и один из этих векторов, то существует множество векторов, которые при скалярном умножении на известный вектор будут давать это значение скалярного произведения. Значит, нельзя однозначно определить действие обратное 13. 12. 2010 Р. Мунипов скалярному произведению. 21
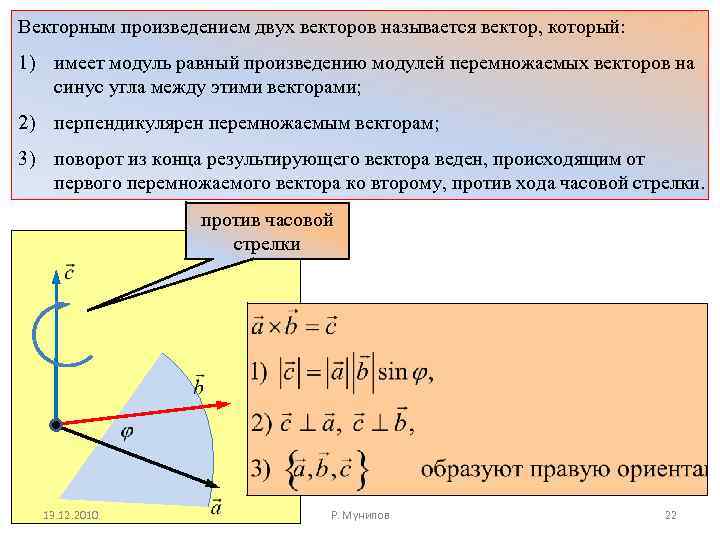
Векторным произведением двух векторов называется вектор, который: 1) имеет модуль равный произведению модулей перемножаемых векторов на синус угла между этими векторами; 2) перпендикулярен перемножаемым векторам; 3) поворот из конца результирующего вектора веден, происходящим от первого перемножаемого вектора ко второму, против хода часовой стрелки. против часовой стрелки 13. 12. 2010 Р. Мунипов 22

Очевидно, векторное произведение вектора на самого себя равно нулевому вектору. Векторное произведение двух векторов равно нулевому вектору если хотя бы один из перемножаемых векторов есть нулевой вектор или перемножаемые вектора коллинеарные (параллельны). Нулевой вектор коллинеарен любому вектору. Значит, векторное произведение двух векторов будет равно нулевому вектору тогда и только тогда, когда 13. 12. 2010 Р. Мунипов перемножаемые вектора коллинеарные. 23
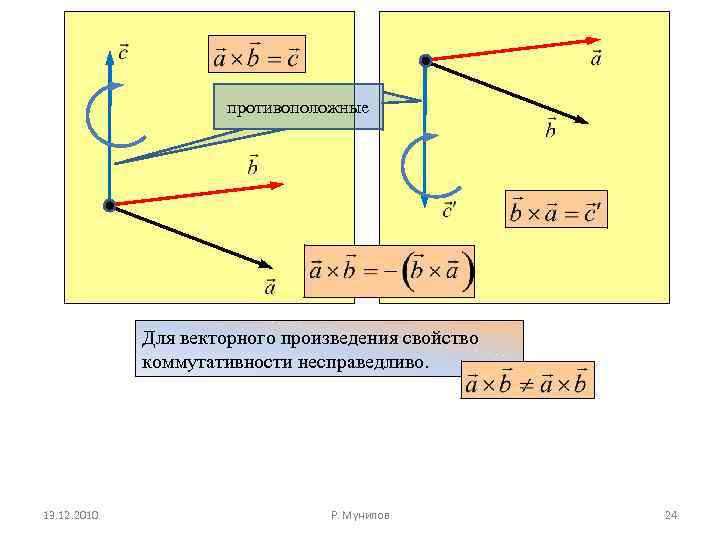
противоположные Для векторного произведения свойство коммутативности несправедливо. 13. 12. 2010 Р. Мунипов 24
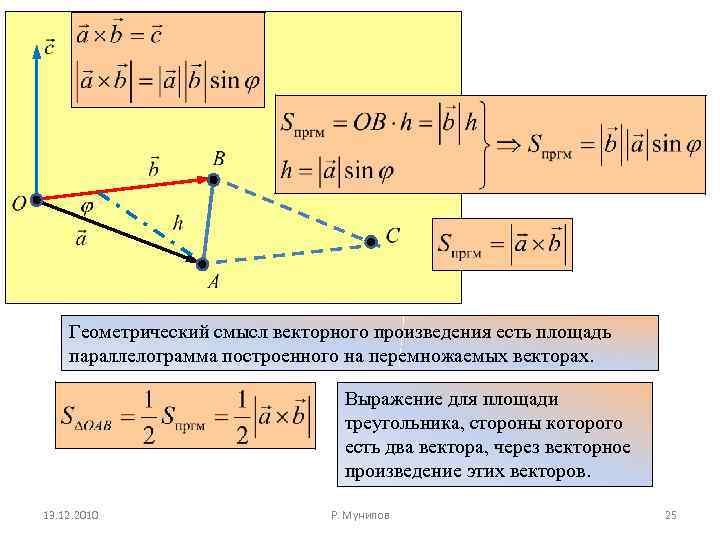
Геометрический смысл векторного произведения есть площадь параллелограмма построенного на перемножаемых векторах. Выражение для площади треугольника, стороны которого есть два вектора, через векторное произведение этих векторов. 13. 12. 2010 Р. Мунипов 25

Для векторного произведения двух векторов справедливо свойство антикомутативности. Для векторного произведения справедливо свойство дистрибутивности. 13. 12. 2010 Р. Мунипов 26
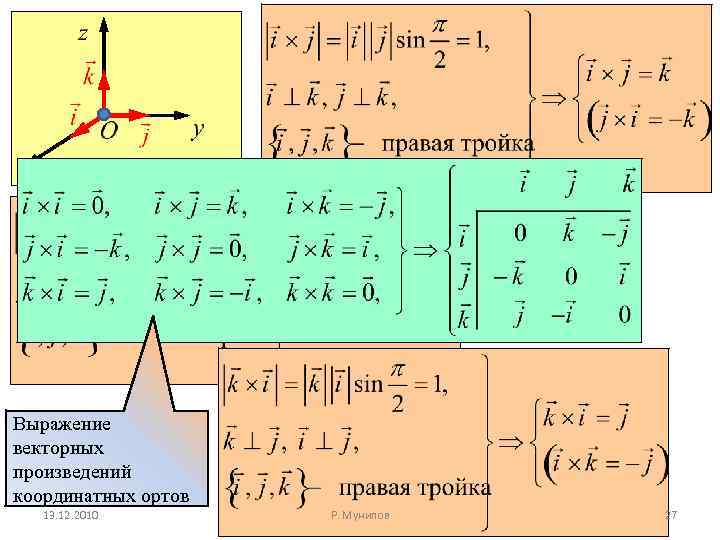
Выражение векторных произведений координатных ортов 13. 12. 2010 Р. Мунипов 27
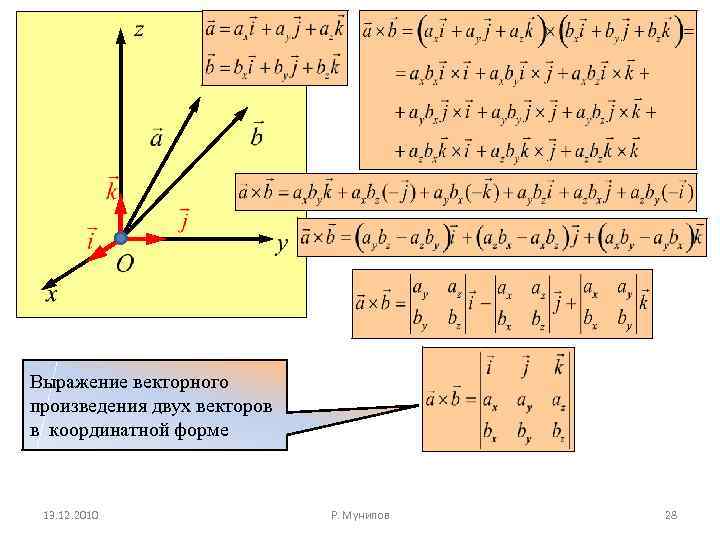
Выражение векторного произведения двух векторов в координатной форме 13. 12. 2010 Р. Мунипов 28
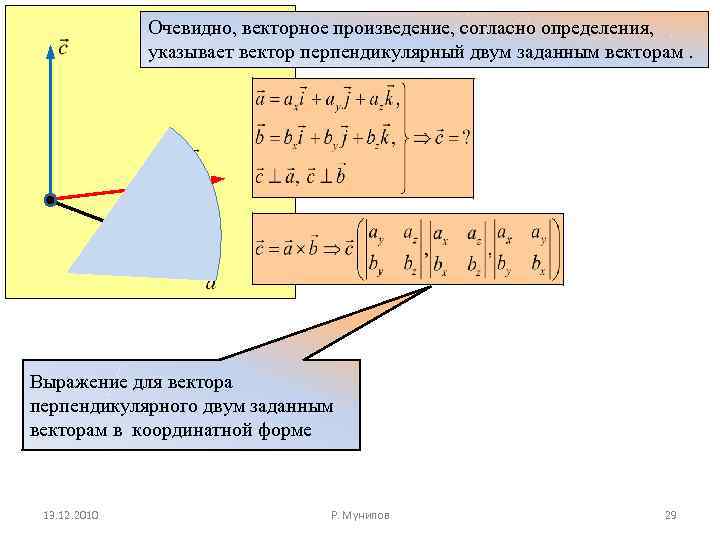
Очевидно, векторное произведение, согласно определения, указывает вектор перпендикулярный двум заданным векторам. Выражение для вектора перпендикулярного двум заданным векторам в координатной форме 13. 12. 2010 Р. Мунипов 29
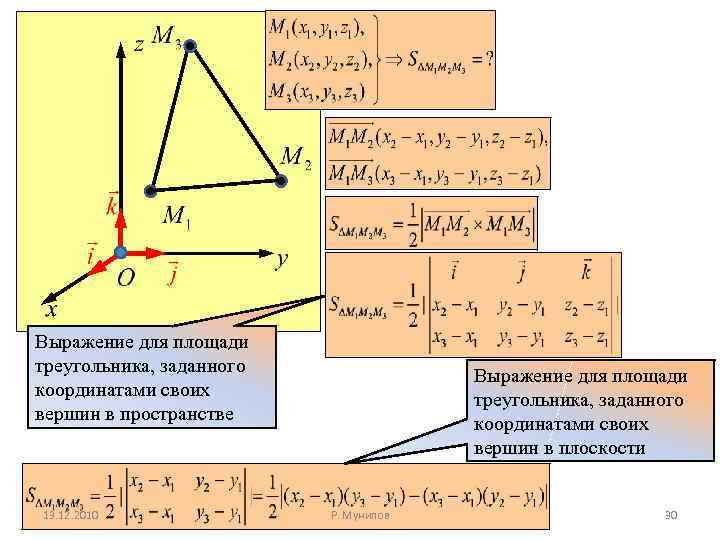
Выражение для площади треугольника, заданного координатами своих вершин в пространстве 13. 12. 2010 Выражение для площади треугольника, заданного координатами своих вершин в плоскости Р. Мунипов 30

Неопределенность действия обратного векторному произведению. Даны векторы и должен быть вектор . Какой чтобы Если известны векторное произведение двух векторов и один из этих векторов, то существует множество векторов, которые при векторном умножении на известный вектор будут давать это значение векторного произведения. Значит, нельзя однозначно определить действие обратное векторному произведению. Любой вектор, начало которого совмещено с началом вектора , а конец расположен на прямой параллельной вектору , будут иметь одинаковые проекции на перпендикуляр, опущенный из конца этого вектора на прямую. 13. 12. 2010 Р. Мунипов 31

Невозможность определить вектор зная его векторное произведение с заданным вектором можно получить и через координаты этих векторов. Определитель системы равен нулю, значит система не имеет единственного решения 13. 12. 2010 Р. Мунипов 32

Основное тождество векторной алгебры произведений векторов: сумма квадратов скалярного и векторного произведений двух векторов равна произведению квадратов этих векторов 13. 12. 2010 Р. Мунипов 33
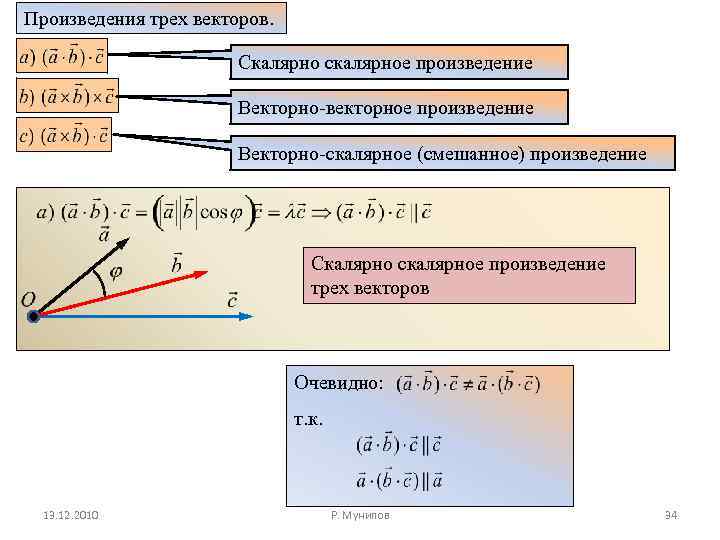
Произведения трех векторов. Скалярно скалярное произведение Векторно-векторное произведение Векторно-скалярное (смешанное) произведение Скалярно скалярное произведение трех векторов Очевидно: т. к. 13. 12. 2010 Р. Мунипов 34
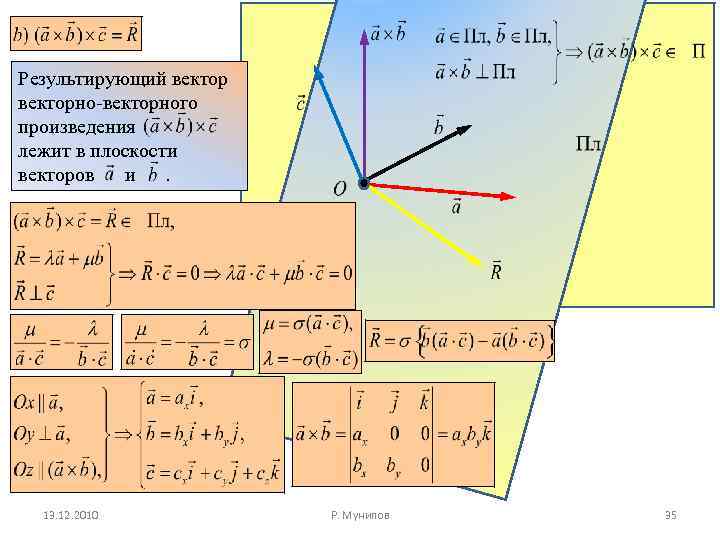
Результирующий векторно-векторного произведения лежит в плоскости векторов и. 13. 12. 2010 Р. Мунипов 35
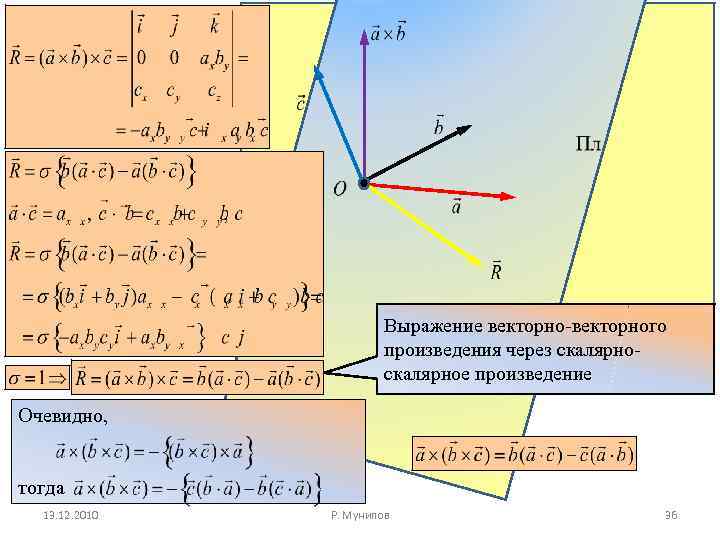
Выражение векторно-векторного произведения через скалярное произведение Очевидно, тогда 13. 12. 2010 Р. Мунипов 36
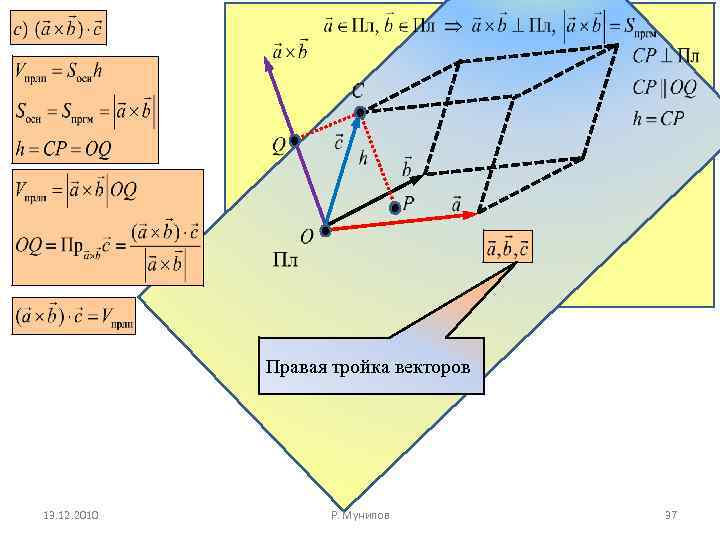
Правая тройка векторов 13. 12. 2010 Р. Мунипов 37
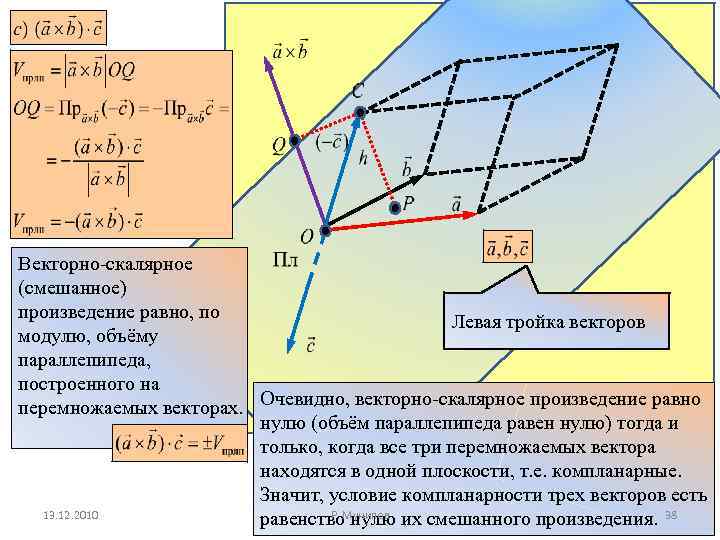
Векторно-скалярное (смешанное) произведение равно, по Левая тройка векторов модулю, объёму параллепипеда, построенного на перемножаемых векторах. Очевидно, векторно-скалярное произведение равно нулю (объём параллепипеда равен нулю) тогда и только, когда все три перемножаемых вектора находятся в одной плоскости, т. е. компланарные. Значит, условие компланарности трех векторов есть 13. 12. 2010 Р. равенство. Мунипов их смешанного произведения. 38 нулю

Для векторно-скалярного произведения трёх векторов справедливо свойство ассоциативности. Для векторно-скалярного произведения трёх векторов справедливо свойство круговой перестановки. Другая форма записи Для векторно-скалярного произведения трёх векторов справедливо свойство дистрибутивности. 13. 12. 2010 Р. Мунипов 39
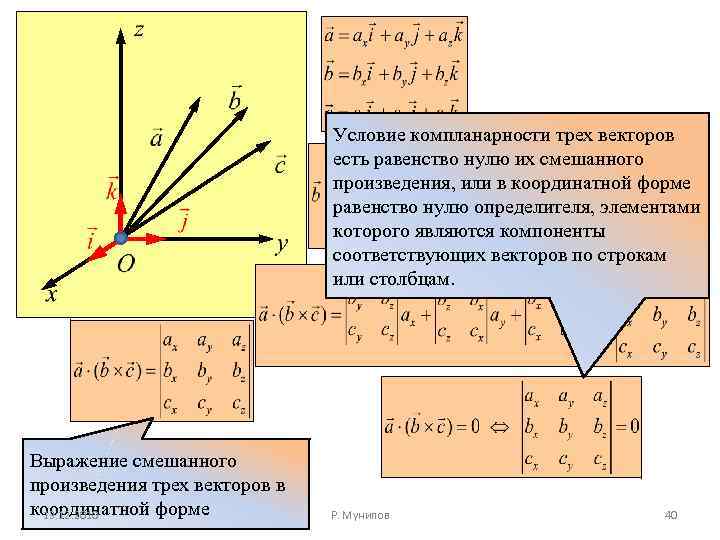
Условие компланарности трех векторов есть равенство нулю их смешанного произведения, или в координатной форме равенство нулю определителя, элементами которого являются компоненты соответствующих векторов по строкам или столбцам. Выражение смешанного произведения трех векторов в координатной форме 13. 12. 2010 Р. Мунипов 40

Простейшие векторные уравнения. Определение вектора по векторному и скалярному уравнениям. Даны три вектора и , и число Какой должен быть вектор чтобы 13. 12. 2010 . Р. Мунипов При этом вектор должны быть перпендикулярными вектору и не перпендикулярен вектору 41

Простейшие векторные уравнения. Определение вектора по векторному уравнению. Даны два вектора взаимно перпендикулярных вектора Какой должен быть вектор и. чтобы обозначим Решение векторного уравнения содержит произвольное число. Частное решение, обозначим 13. 12. 2010 , расположено в плоскости перпендикулярной плоскости векторов и Р. Мунипов 42
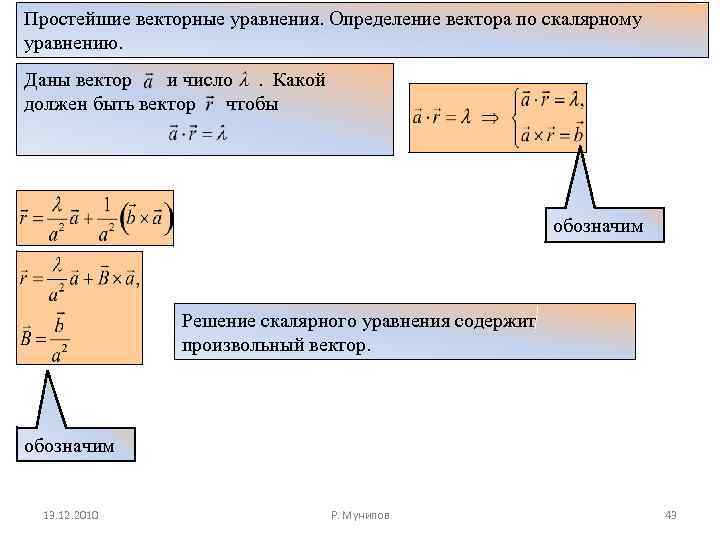
Простейшие векторные уравнения. Определение вектора по скалярному уравнению. Даны вектор и число. Какой должен быть вектор чтобы обозначим Решение скалярного уравнения содержит произвольный вектор. обозначим 13. 12. 2010 Р. Мунипов 43

Простейшие векторные уравнения. Определение вектора по трем скалярным произведениям. Даны три некомпланарных вектора три числа. Какой должен быть вектор чтобы 13. 12. 2010 и Р. Мунипов 44

Простейшие векторные уравнения. Решение векторного уравнения. Даны два вектора и , и число Какой должен быть вектор чтобы 13. 12. 2010 . Р. Мунипов 45

Простейшие векторные уравнения. Разложение вектора по трем некомпланарным векторам. Даны три некомпланарных вектора и и вектор. Каковы должен быть числа чтобы , В силу некомпланарности векторов определитель отличен от нуля. Значит система уравнений имеет единственное решение. 13. 12. 2010 Р. Мунипов 46
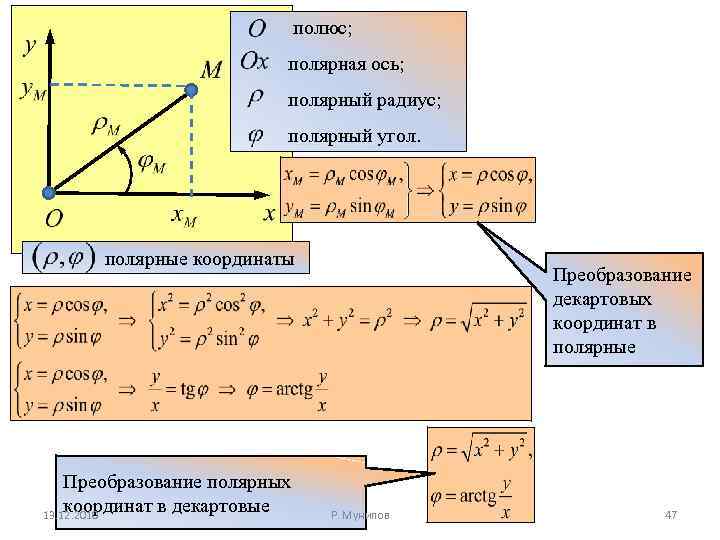
полюс; полярная ось; полярный радиус; полярный угол. полярные координаты Преобразование полярных координат в декартовые 13. 12. 2010 Преобразование декартовых координат в полярные Р. Мунипов 47
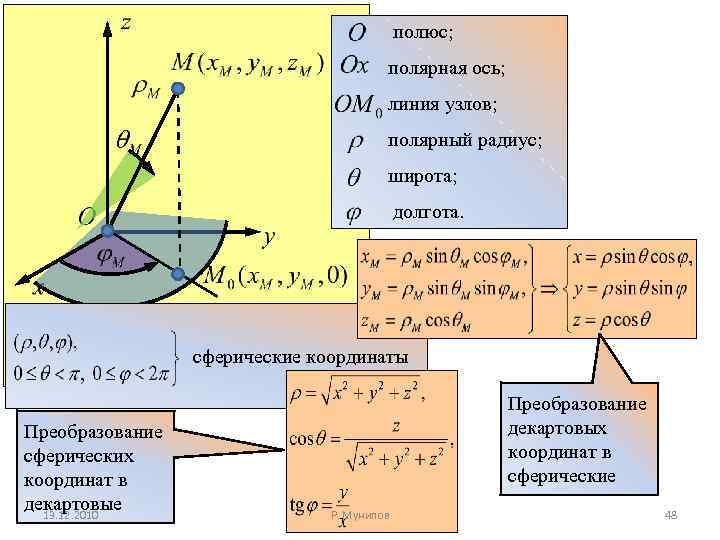
полюс; полярная ось; линия узлов; полярный радиус; широта; долгота. сферические координаты Преобразование сферических координат в декартовые 13. 12. 2010 Преобразование декартовых координат в сферические Р. Мунипов 48
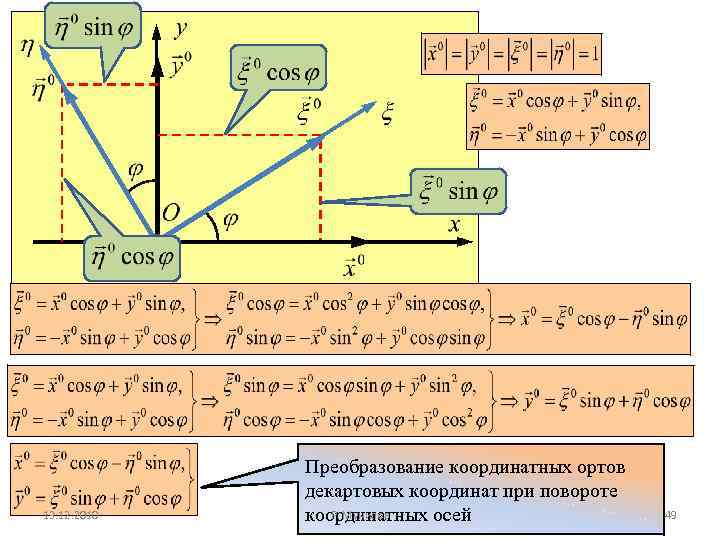
13. 12. 2010 Преобразование координатных ортов декартовых координат при повороте Р. Мунипов координатных осей 49
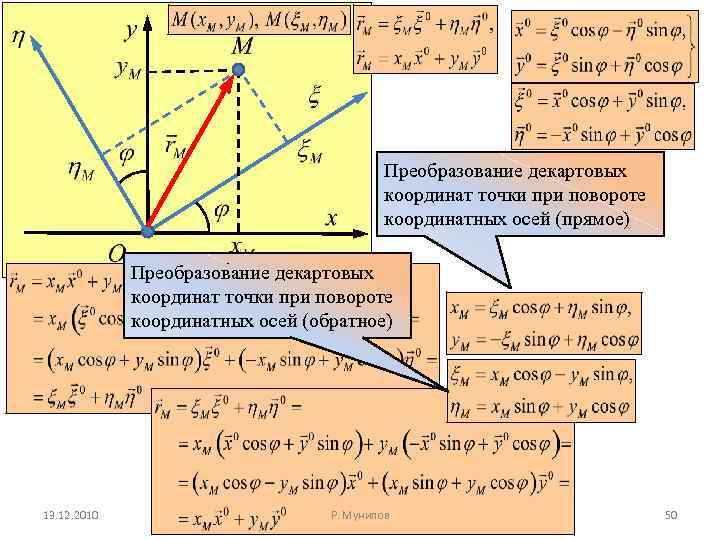
Преобразование декартовых координат точки при повороте координатных осей (прямое) Преобразование декартовых координат точки при повороте координатных осей (обратное) 13. 12. 2010 Р. Мунипов 50

Матрица преобразования координат при повороте координатных осей (прямое преобразование) в плоскости матрица преобразования координат при повороте координатных осей (обратное преобразование) в плоскости причем, 13. 12. 2010 Р. Мунипов 51
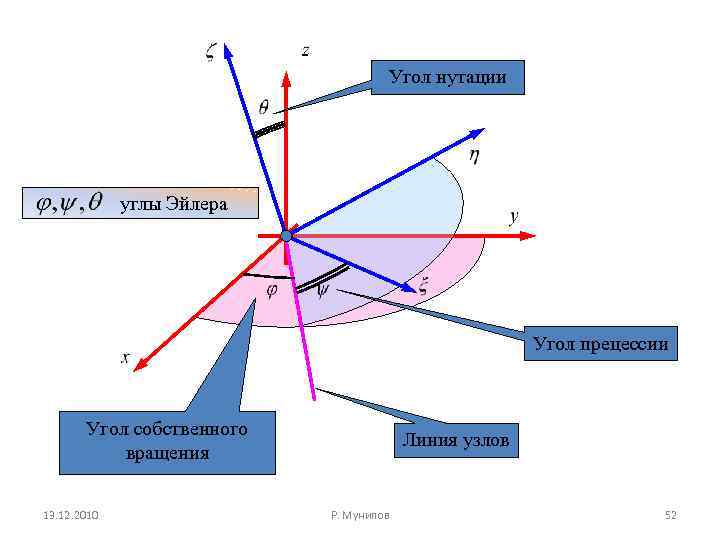
Угол нутации углы Эйлера Угол прецессии Угол собственного вращения 13. 12. 2010 Линия узлов Р. Мунипов 52

Матрица преобразования координат при повороте координатных осей (прямое преобразование) в пространстве, через углы Эйлера 13. 12. 2010 Р. Мунипов 53
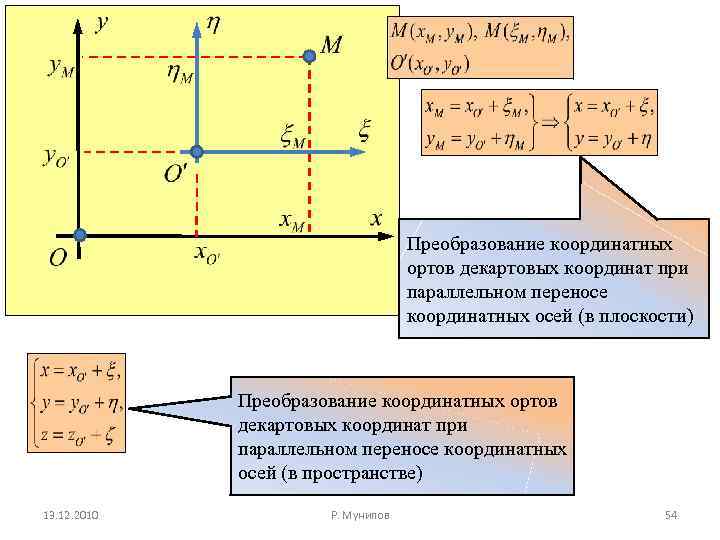
Преобразование координатных ортов декартовых координат при параллельном переносе координатных осей (в плоскости) Преобразование координатных ортов декартовых координат при параллельном переносе координатных осей (в пространстве) 13. 12. 2010 Р. Мунипов 54
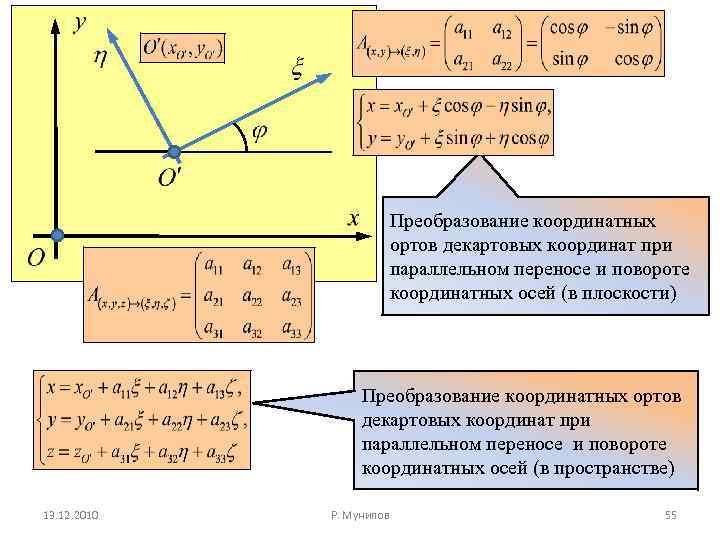
Преобразование координатных ортов декартовых координат при параллельном переносе и повороте координатных осей (в плоскости) Преобразование координатных ортов декартовых координат при параллельном переносе и повороте координатных осей (в пространстве) 13. 12. 2010 Р. Мунипов 55
Вектор2.pptx