Вектор ПОНЯТТЯ ПРО ВЕКТОР Поняття про вектор

Вектор ПОНЯТТЯ ПРО ВЕКТОР

Поняття про вектор Вільям Роуен Гамільтон 1805 - 1865 видатний ірландський математик і фізик XIX століття. термін вектор (від лат. Vector - "що має") вперше з'явився в 1845 р. в ірландського математика Вільяма Гамільтона

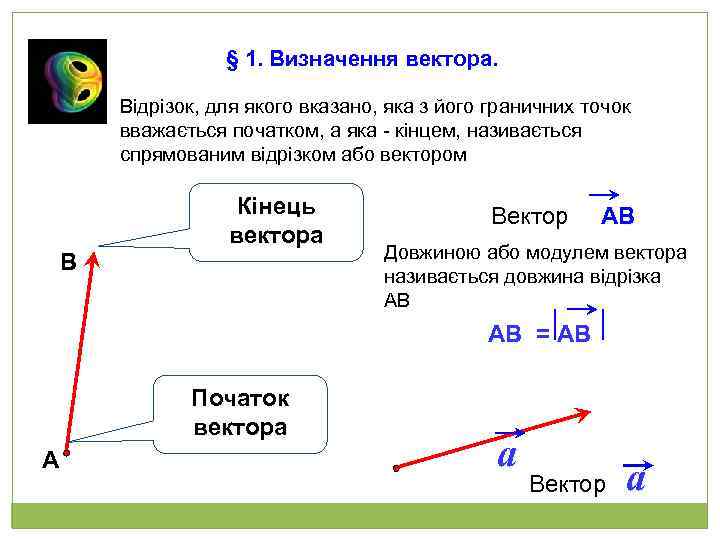§ 1. Визначення вектора. Відрізок, для якого вказано, яка з його граничних точок вважається початком, а яка - кінцем, називається спрямованим відрізком або вектором В Кінець вектора Вектор АВ Довжиною або модулем вектора називається довжина відрізка АВ АВ = АВ Початок вектора А a Вектор a

§ 1. Визначення вектора. Будь яка точка площини також є вектором. У цьому випадку вектор називається нульовим. Вектор MM M Вектор 0 Початок нульового вектора збігається з його кінцем, тому нульовий вектор не має якого-небудь певного напрямку. Інакше кажучи, будь-який напрямок можна вважати напрямком нульового вектора. Довжина нульового вектора вважається рівною нулю. MM = 0

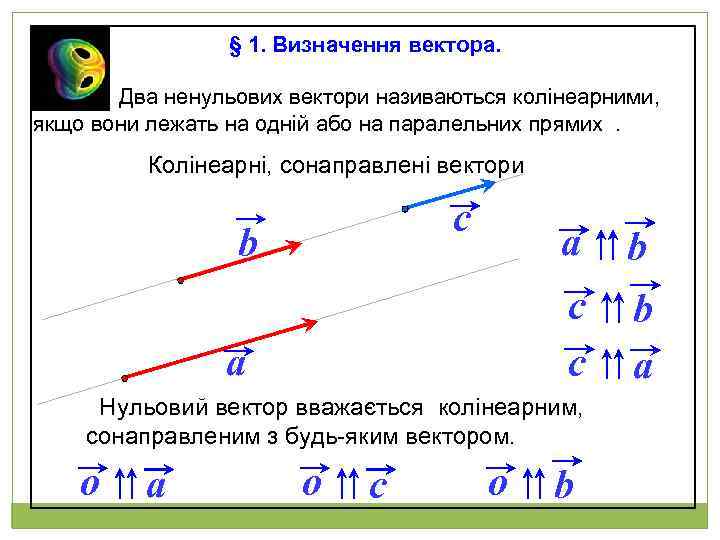§ 1. Визначення вектора. Два ненульових вектори називаються колінеарними, якщо вони лежать на одній або на паралельних прямих . Колінеарні, сонаправлені вектори c a a b c c b b a Нульовий вектор вважається колінеарним, сонаправленим з будь-яким вектором. o a o c o b

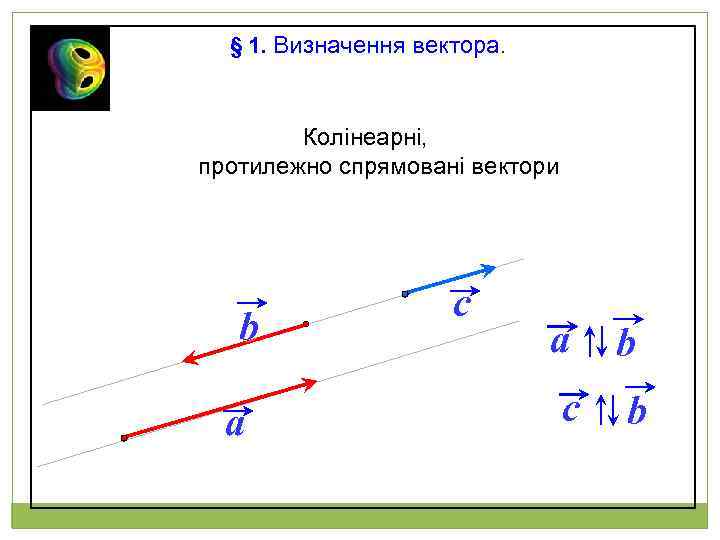§ 1. Визначення вектора. Колінеарні, протилежно спрямовані вектори b a c a b c b

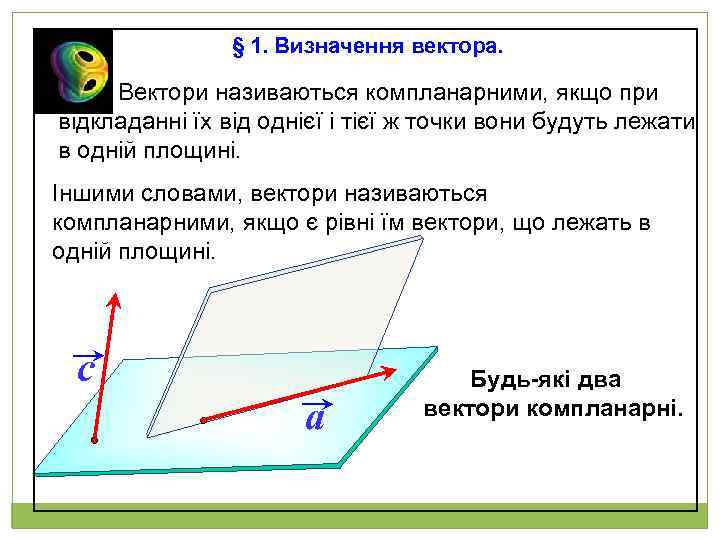§ 1. Визначення вектора. Вектори називаються компланарними, якщо при відкладанні їх від однієї і тієї ж точки вони будуть лежати в одній площині. Іншими словами, вектори називаються компланарними, якщо є рівні їм вектори, що лежать в одній площині. c a Будь-які два вектори компланарні.

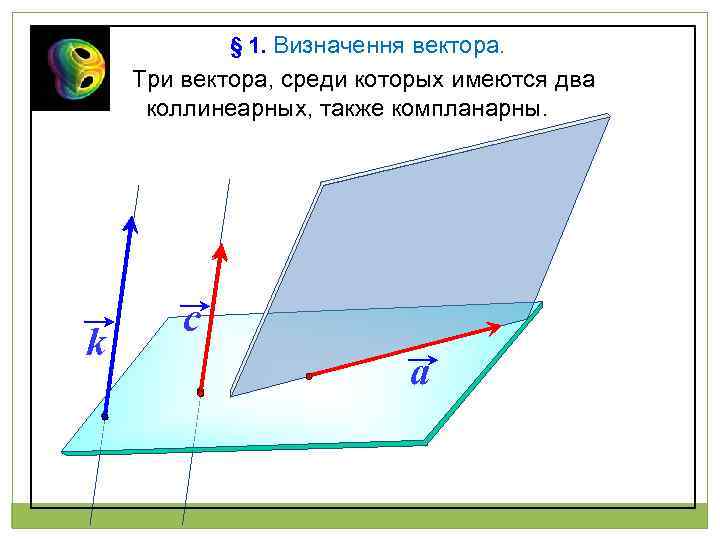§ 1. Визначення вектора. Три вектора, среди которых имеются два коллинеарных, также компланарны. k c a

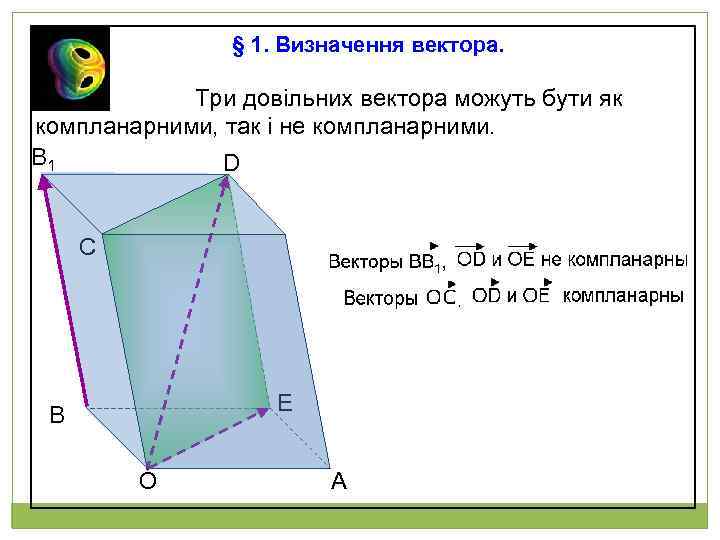§ 1. Визначення вектора. Три довільних вектора можуть бути як компланарними, так і не компланарними. B 1 D C Е В О А

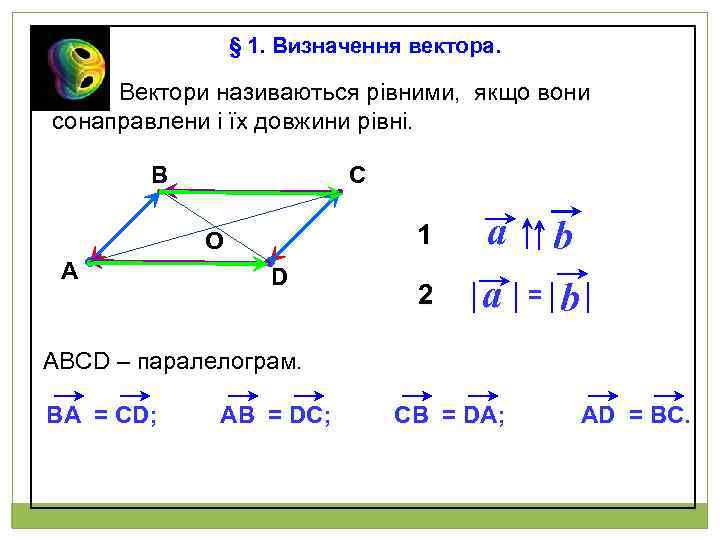§ 1. Визначення вектора. Вектори називаються рівними, якщо вони сонаправлени і їх довжини рівні. В С 1 О А D a 2 a b = b АВСD – паралелограм. ВA = CD; AВ = DC; CВ = DA; AD = BC.

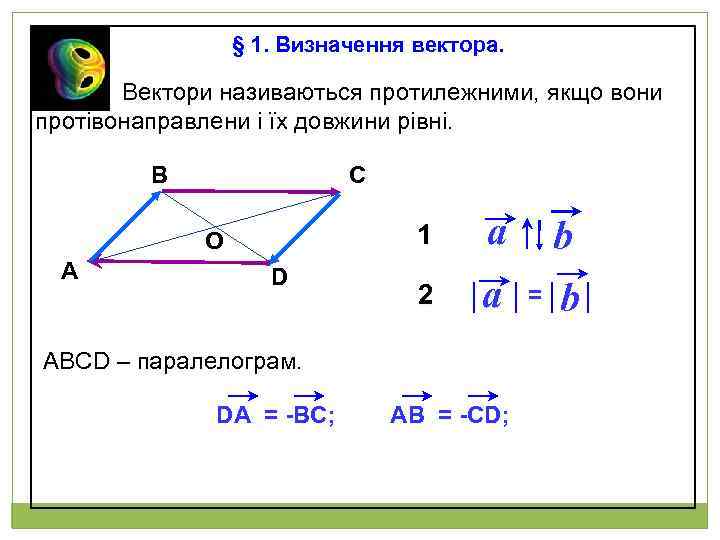§ 1. Визначення вектора. Вектори називаються протилежними, якщо вони протівонаправлени і їх довжини рівні. В С 1 О А D a 2 a АВСD – паралелограм. DA = -BC; AВ = -CD; b = b

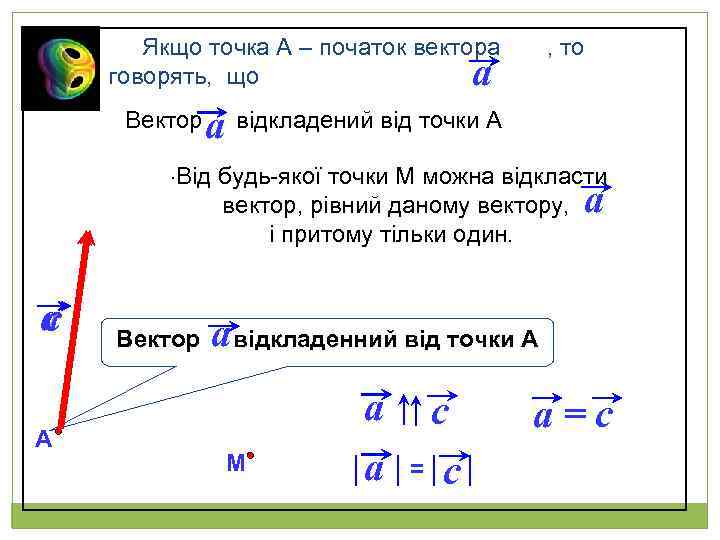Якщо точка А – початок вектора , то говорять, що a a Вектор відкладений від точки А. Від будь-якої точки М можна відкласти вектор, рівний даному вектору, і притому тільки один. a a c А Вектор a відкладенний від точки А М a a c = c a=c

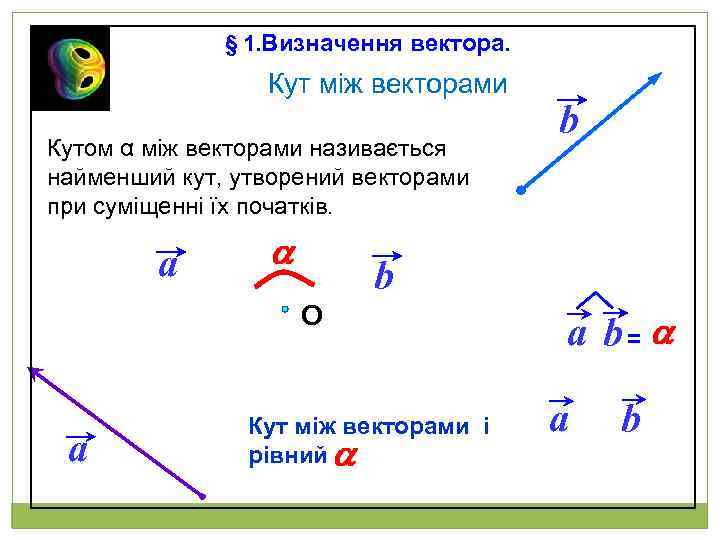§ 1. Визначення вектора. Кут між векторами Кутом α між векторами називається найменший кут, утворений векторами при суміщенні їх початків. a a b О a b Кут між векторами і рівний a a b= a a b

§ 1. Визначення вектора. Для колінеарних векторів або Два вектора називаються ортогональними, якщо кут між ними дорівнює 90. c b b^c

Дякую за увагу!