Вейвлет-преобразование и его использование в рамках процедур обработки данных Автор: Лагунова Надежда, 410 гр.
Содержание История Вейвлеты и зачем они нужны Классификация Основы вейвлет-преобразования Примеры Вопросы к зачету Литература Милая картиночка на десерт
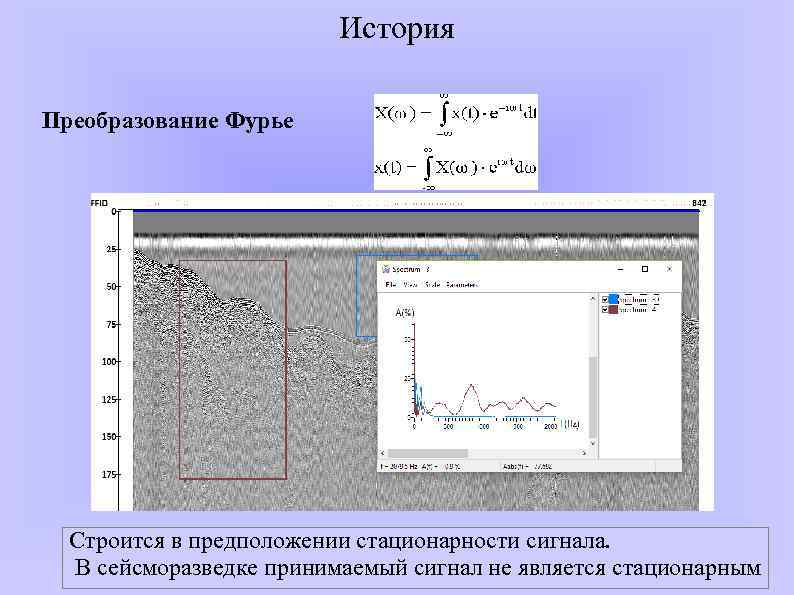
История Преобразование Фурье Строится в предположении стационарности сигнала. В сейсморазведке принимаемый сигнал не является стационарным
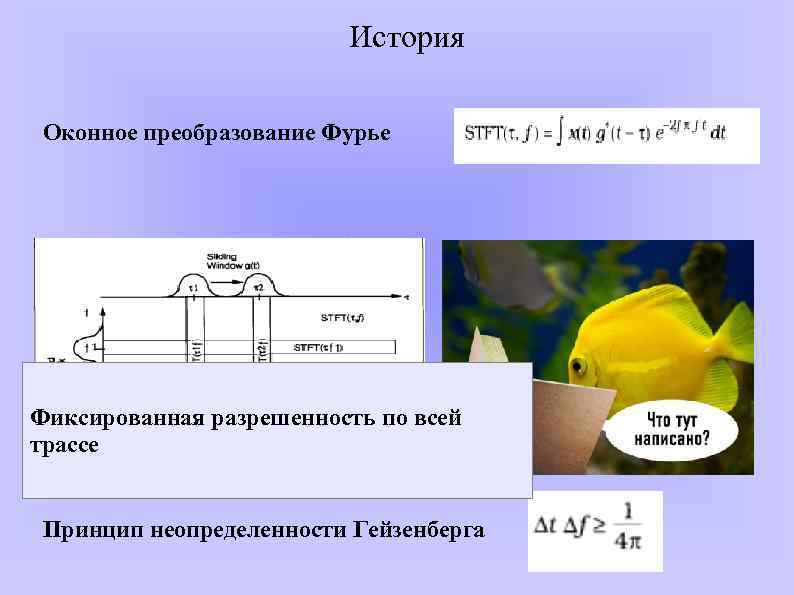
История Оконное преобразование Фурье Фиксированная разрешенность по всей трассе Принцип неопределенности Гейзенберга
Вейвлеты и зачем они нужны Семейство математических функций Промежуточные по локализованности между гармоническими и импульсными функциями Образуют базис (в нашем случае это необходимо) Получаются с помощью сдвига и растяжений по временной оси из материнской функции Имеют нулевую площадь
Вейвлеты и зачем они нужны Частотная и пространственная локализация особенностей сигнала Можно добиться разных соотношений неопределенности (разрешения)
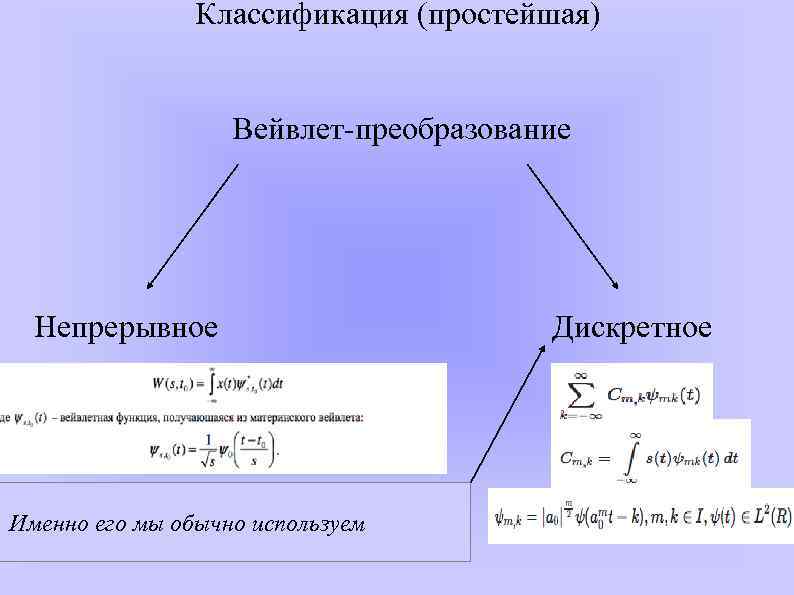
Классификация (простейшая) Вейвлет-преобразование Непрерывное Именно его мы обычно используем Дискретное
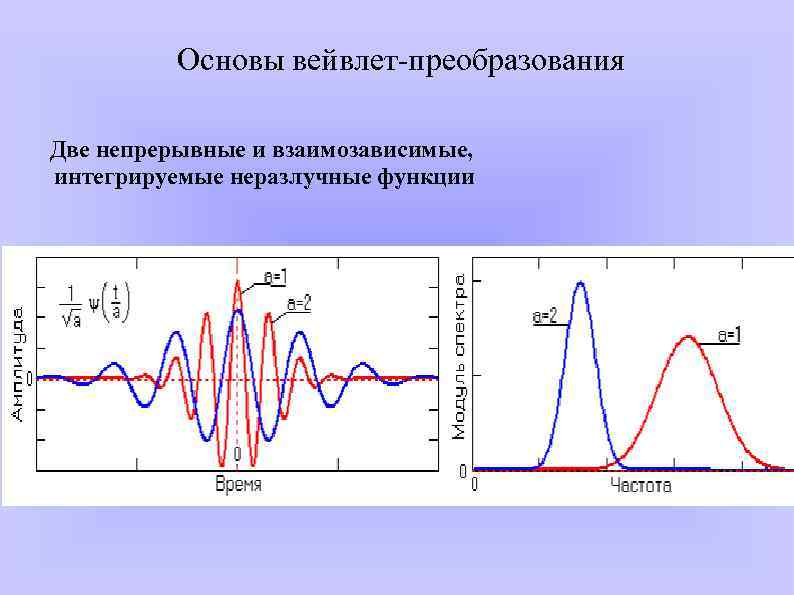
Основы вейвлет-преобразования Две непрерывные и взаимозависимые, интегрируемые неразлучные функции
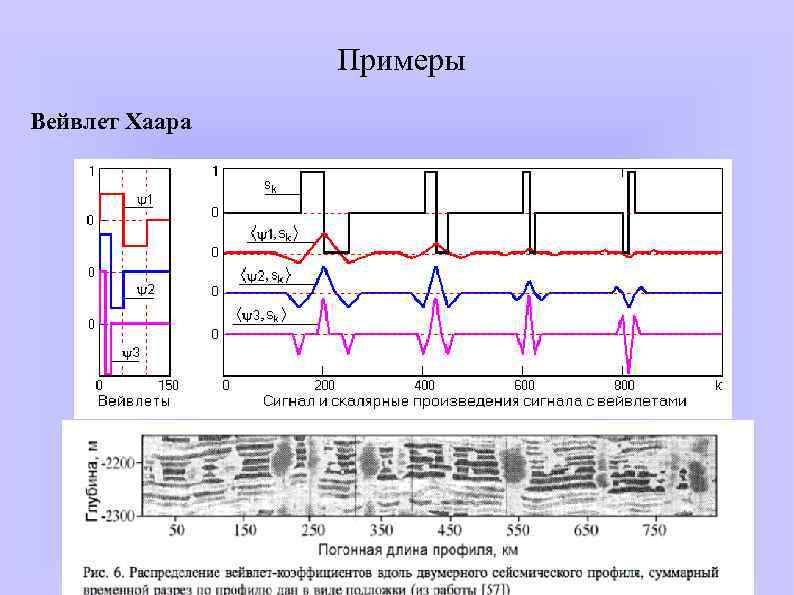
Примеры Вейвлет Хаара
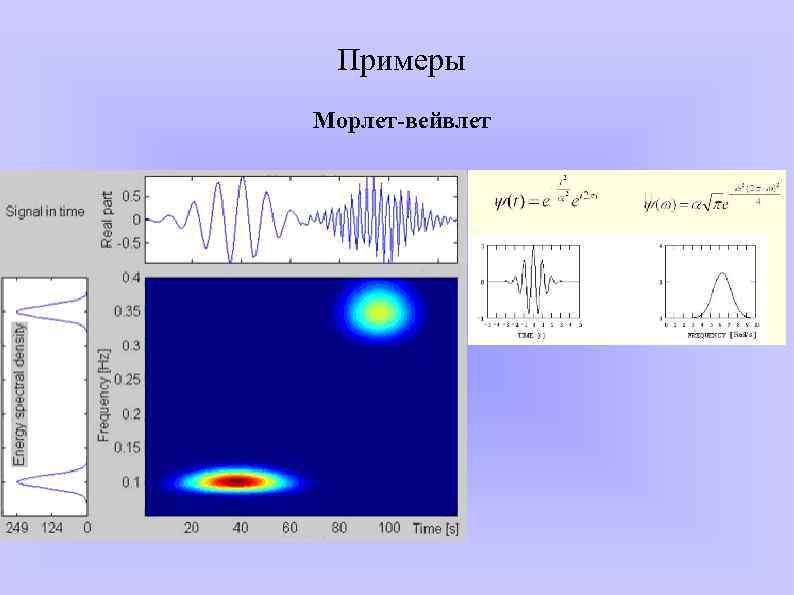
Примеры Морлет-вейвлет
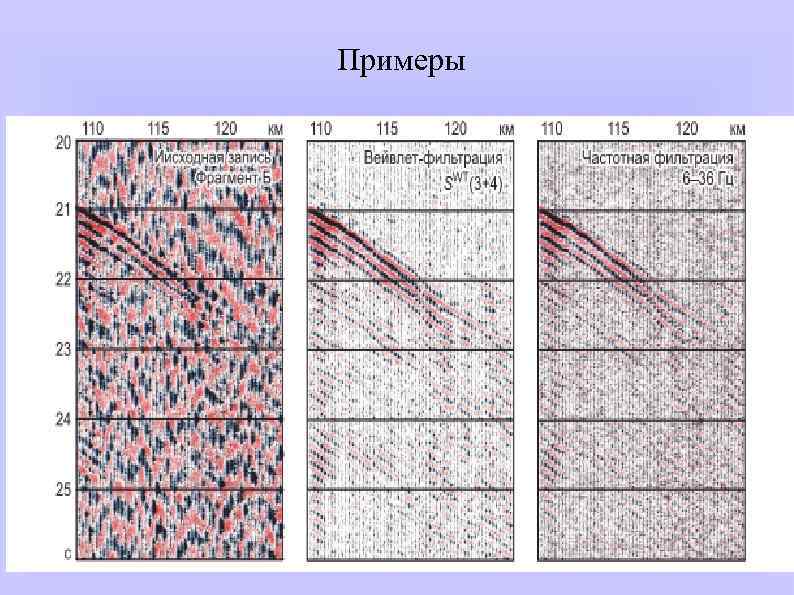
Примеры
Вопросы к зачету Недостаток преобразования Фурье Что такое вейвлет? Что такое вейвлет-преобразование и чем оно хорошо?
Литература «Wavelets and signal processing» Rioul, Vetterli ru. bmstu. wiki/Анализ_сигналов_на_основе_вейвл ет-преобразования
Не забывайте про обратное преобразование Меня плющит
Скачать презентацию Вейвлет-преобразование и его использование в рамках процедур обработки
vei_774_vlet-preobrazovanie_Lagunova.ppt