Vectors and scalar Objectives: Add and subtract vectors

Vectors and scalar Objectives: Add and subtract vectors Find the components of a vector Reconstruct the magnitude and direction of a vector Solve problems with vectors Homework: Pages 1,2a and 10; Стр. 3-4. Data Booklet Problems (paper)

Vectors There are two kinds of quantities in physics: scalar quantities and vector quantities. Vector quantities is the quantities which has magnitude and direction. It is represented by straight line with an arrow at one end:

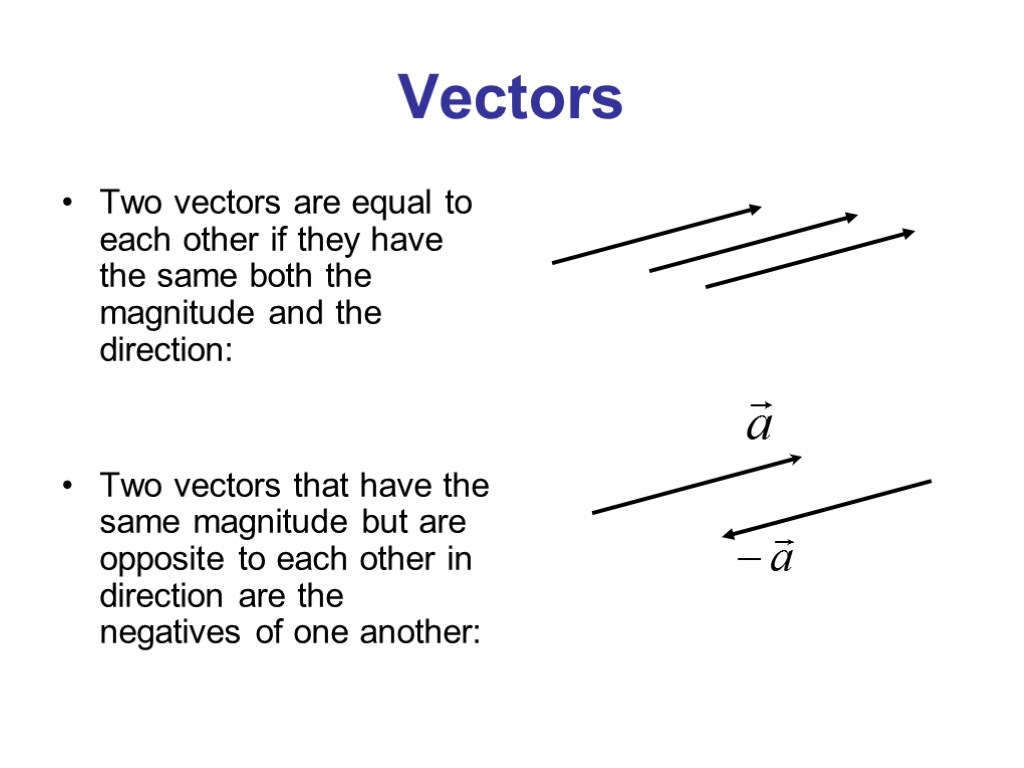
Vectors Two vectors are equal to each other if they have the same both the magnitude and the direction: Two vectors that have the same magnitude but are opposite to each other in direction are the negatives of one another:

Multiplication of a vector by a scalar If the vector a is multiplied by the number k, then the resulting vector ka has the same direction as a if k>0 and opposite to a if k<0.

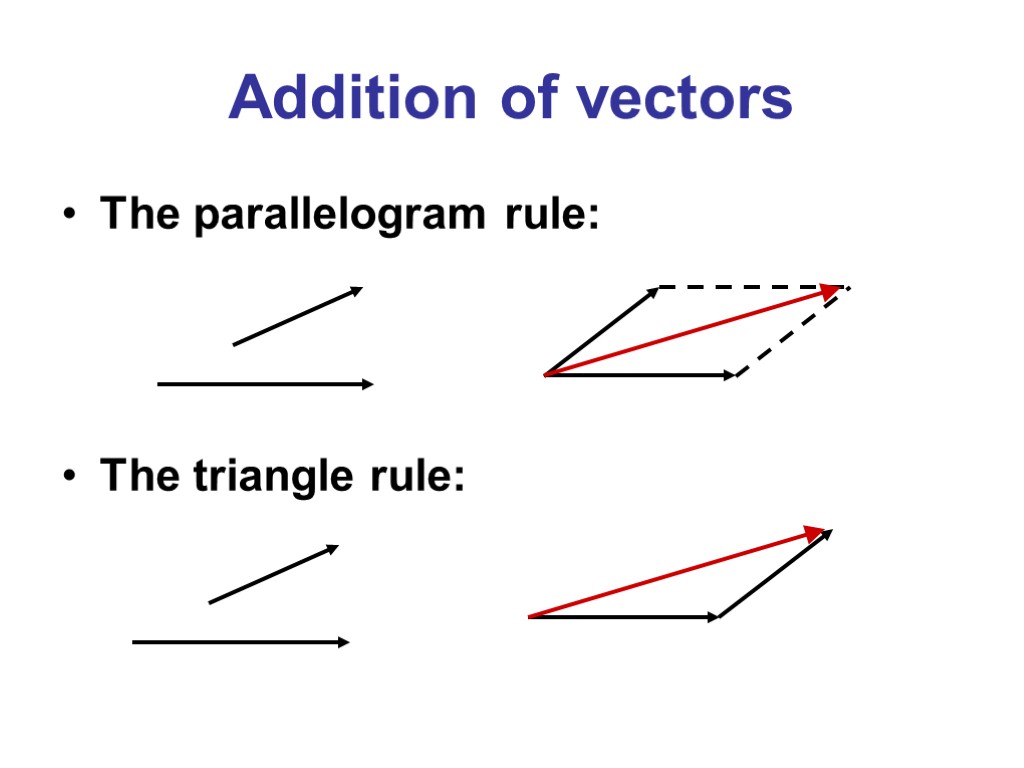
Addition of vectors The parallelogram rule: The triangle rule:

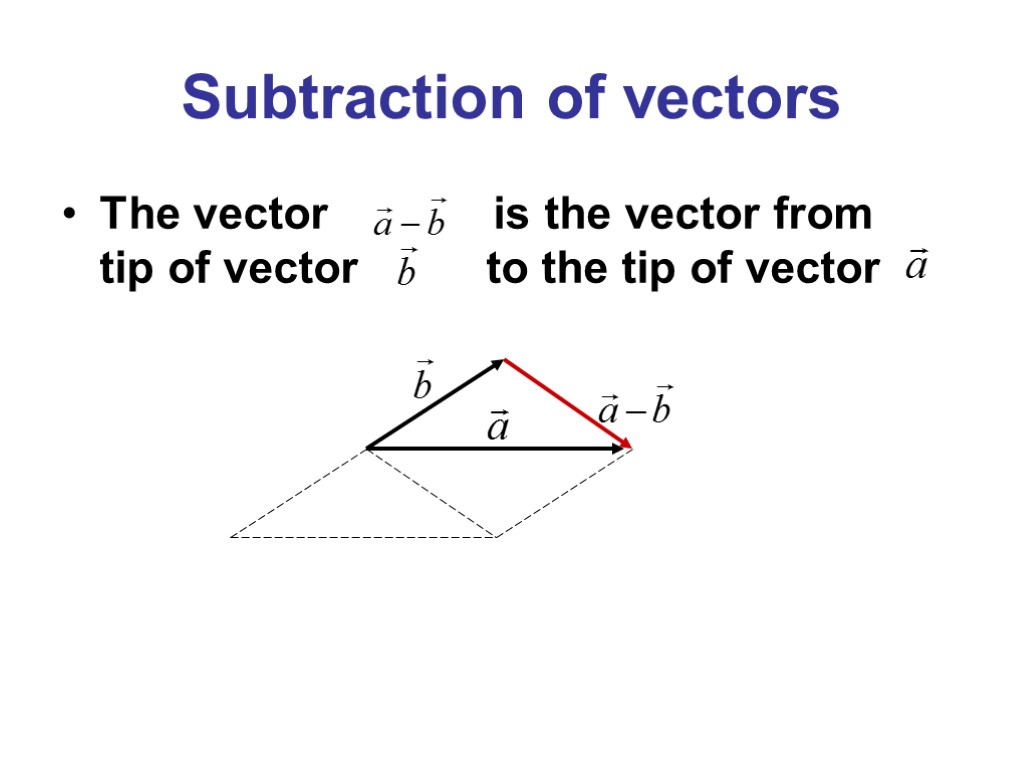
Subtraction of vectors The vector is the vector from tip of vector to the tip of vector

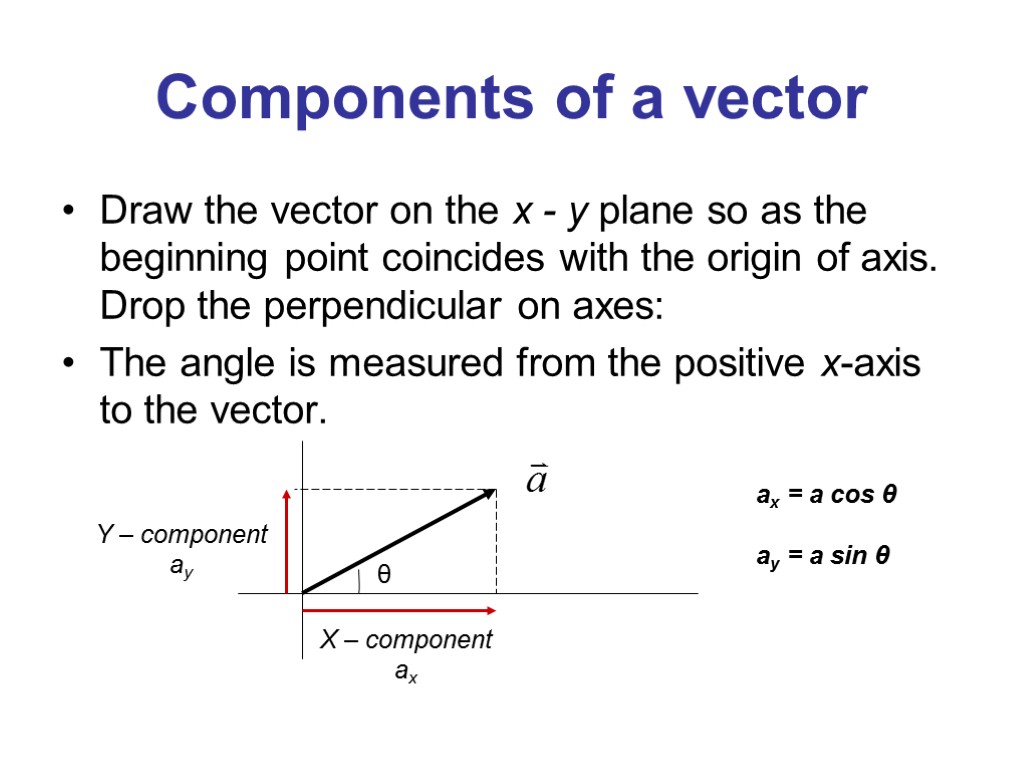
Components of a vector Draw the vector on the x - y plane so as the beginning point coincides with the origin of axis. Drop the perpendicular on axes: The angle is measured from the positive x-axis to the vector. θ ax = a cos θ ay = a sin θ

Resolving a vector into it’s components in two dimensions at 90º angle: By Pythagorean theorem: The direction is found from: θ Adding vectors by component: