Vectors and scalar Homework Pages 1 2

Vectors and scalar Homework: • Pages 1, 2 a and 10; • Стр. 3 -4. • Data Booklet • Problems (paper) • • Objectives: Add and subtract vectors Find the components of a vector Reconstruct the magnitude and direction of a vector Solve problems with vectors

Vectors • There are two kinds of quantities in physics: scalar quantities and vector quantities. • Vector quantities is the quantities which has magnitude and direction. • It is represented by straight line with an arrow at one end:

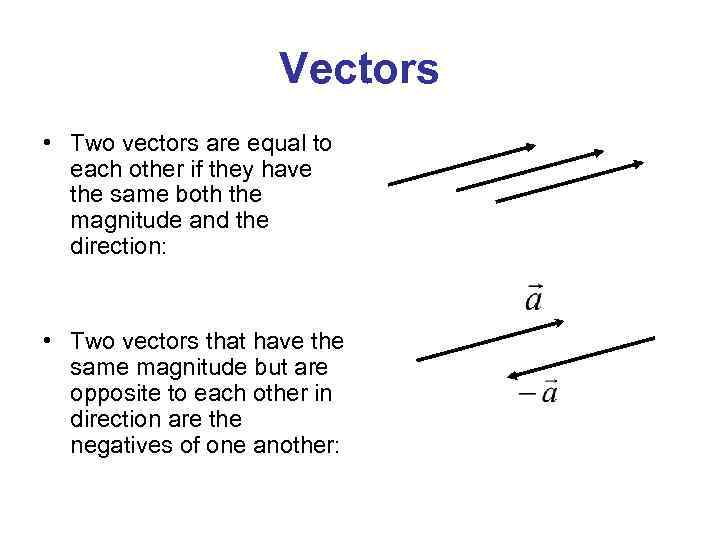Vectors • Two vectors are equal to each other if they have the same both the magnitude and the direction: • Two vectors that have the same magnitude but are opposite to each other in direction are the negatives of one another:

Multiplication of a vector by a scalar • If the vector a is multiplied by the number k, then the resulting vector ka has the same direction as a if k>0 and opposite to a if k<0.

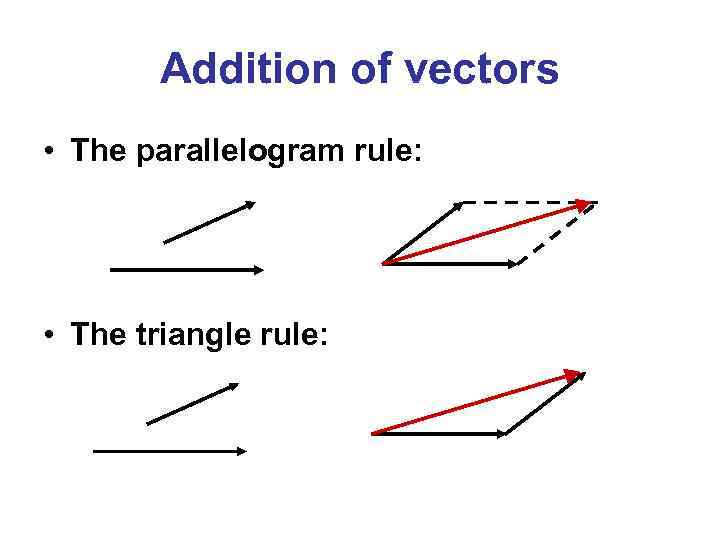Addition of vectors • The parallelogram rule: • The triangle rule:

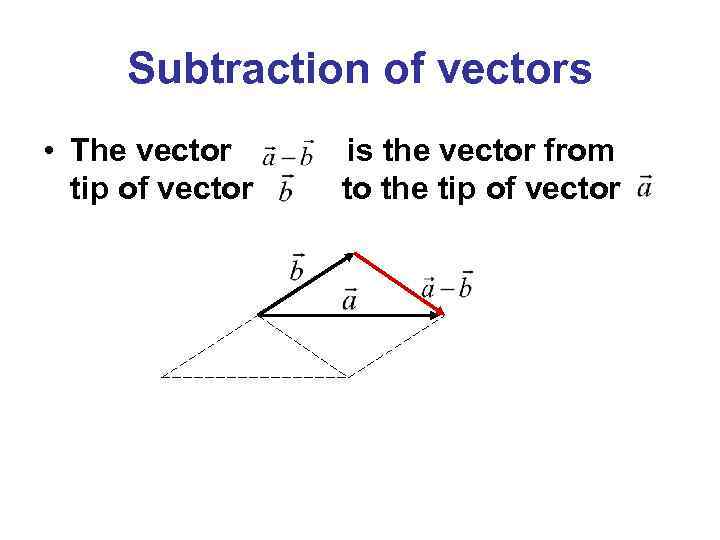Subtraction of vectors • The vector tip of vector is the vector from to the tip of vector

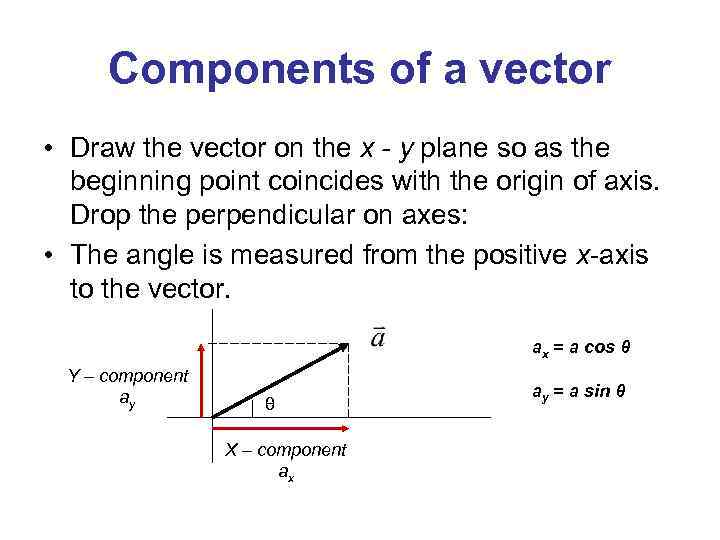Components of a vector • Draw the vector on the x - y plane so as the beginning point coincides with the origin of axis. Drop the perpendicular on axes: • The angle is measured from the positive x-axis to the vector. ax = a cos θ Y – component ay θ X – component ax ay = a sin θ

• Resolving a vector into it’s components in two dimensions at 90º angle: Fy θ Fx By Pythagorean theorem: The direction is found from: • Adding vectors by component: