квест по теории вероятностей.pptx
- Количество слайдов: 30

Веб-квест «Предмет теории вероятностей. Событие. Вероятность события»

Уважаемые студенты! Перед Вами стоят следующие задачи: - осуществить поиск и систематизацию информации об истории и основных понятиях теории вероятностей; - разобраться в примерах решения простейших вероятностных задач и решать их самостоятельно; - выполнить экспериментальные творческие работы по определению статистической вероятности случайных событий. Предмет исследования – различные задачи, связанные с определением вероятности случайного события На эти и многие другие вопросы вы узнаете ответы, если примете в работе веб-квеста. Центральное задание

1. Выберите себе роль, от лица которой нужно будет пройти веб-квест. 2. Познакомьтесь с главной задачей веб-квеста. 3. Изучите интернет-ресурсы в соответствии со своей ролью. 4. Ответьте на вопросы, которые поставлены перед Вами. 5. Оформите отчет о выполненном задании (сообщение, презентация, буклет и т. д. ). Перед началом работы ознакомьтесь с критериями оценки веб-квеста. 6. Проведите защиту своей работы. 7. Сделайте общие выводы. 8. Выполните задания для самостоятельного решения Порядок работы
РОЛИ ИСТОРИК ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ ТЕОРЕТИК КРИТЕРИИ ОЦЕНОК ТВОРЧЕСКИХ РАБОТ ПРАКТИК ИТОГИ ИССЛЕДОВАТЕЛЬ ЭКСПЕРИМЕНТАТОР В НАЧАЛО

ИСТОРИК Вы выбрали роль историков. Выполните следующие задания: 1. Дайте определение теории вероятностей. 2. Выясните, что является предметом изучения теории вероятностей, т. е. что изучает теория вероятностей. 3. Узнайте, когда и как возникла теория вероятностей. Какие задачи привели к формированию основ этой области математики? 4. Перечислите ученых-основоположников теории вероятностей, познакомьтесь с их биографиями. 5. Какое отношение к теории вероятностей имеют игральные кости? Для ответа на поставленные вопросы изучите предлагаемые на странице «Порядок работы» интернет-ресурсы, а также найдите их самостоятельно. Ответы оформите в виде сообщения с презентацией. В отчете укажите ссылки, которыми вы пользовались. ИНТЕРНЕТ РЕСУРСЫ

ТЕОРЕТИК Вы выбрали роль теоретиков. Вам нужно найти ответы об основных понятиях теории вероятностей: 1. Определение и предмет изучения теории вероятностей. 2. Что такое опыт (испытание) в теории вероятностей? 3. Определение события. 4. Виды событий: достоверные, невозможные, случайные. Приведите примеры. 5. Виды случайных событий: элементарные (составные); несовместные (совместные); равновозможные (неравновозможные). Приведите примеры. 6. Классическое определение вероятности, формула. 7. Свойства вероятности. 8. Статистическое определение вероятности, формула. Для ответа на поставленные вопросы изучите предлагаемые на странице «Порядок работы» интернет-ресурсы, а также найдите их самостоятельно. Ответы оформите в виде сообщения с презентацией. В отчете укажите ссылки, которыми вы пользовались. ИНТЕРНЕТ РЕСУРСЫ

ПРАКТИК Вы выбрали роль практиков. Вам нужно найти ответы на следующие вопросы: 1. Классическое определение вероятности, формула. 2. Свойства вероятности. 3. Статистическое определение вероятности, формула. 4. Разобраться с алгоритмом решения простейших задач по теории вероятностей по ссылке Примеры решения задач. 5. Изучите справочные материалы и выполните задание № 1 из раздела Проверьте себя. 6. Представьте приемы решения задач. 7. Если все получилось, переходите к разделу Задачи для самостоятельного решения. 8. В разделе «Итоги» посмотрите, как оформить работу. Для ответа на поставленные вопросы изучите предлагаемые интернет-ресурсы, а также найдите их самостоятельно. Ответы оформите в виде сообщения с презентацией. В отчете укажите ссылки, которыми вы пользовались. ИНТЕРНЕТ РЕСУРСЫ

ИССЛЕДОВАТЕЛЬ Вы выбрали роль исследователя. Вам предстоит выполнить исследовательскую работу: определить самую распространенную и самую редкую буквы в русском и английском языке. Для этого необходимо взять произвольный газетный (журнальный) текст с определенным количеством букв (для удобства подсчета возьмите 1000 букв). Подсчитайте количество каждой буквы алфавита в данном тексте. По формуле статистической вероятности Р(А)=m/n, где n - общее количество букв в тексте, m – количество каждой буквы в тексте, определите вероятность использования каждой буквы в данном тексте. Результаты внесите в таблицу. Буква Количество буквы в тексте Вероятность использования буквы в тексте Выбранный газетный текст приложите к отчету. При оформлении сообщения с презентацией укажите цель работы, приборы и материалы, ход работы, вывод. Подумайте и напишите: где и с какой целью можно использовать результаты вашей работы. ИНТЕРНЕТ РЕСУРСЫ

ЭКСПЕРИМЕНТАТОР Вы выбрали роль экспериментаторов. Вам предстоит выполнить опыт с монетой: определить вероятность выпадения герба (цифры) при сталкивании монеты со стола. Зафиксируйте высоту стола, достоинство и первоначальное положение монеты на столе. Аккуратно сталкивая монету со стола, отметьте, на какую сторону упадет монета. Проведите опыт 50 раз. Изменив первоначальное положение монеты, сделайте снова опыт 50 раз. Не обращая внимания на первоначальное положение монеты на столе, сложите результаты предыдущих опытов и внесите все данные в таблицу. Первоначальное положение монеты Количество выпадений герба Количество выпадений цифры Вероятность выпадения герба Вероятность выпадения цифры По формуле статистической вероятности Р(А)=m/n, где n - общее число бросаний, m - число выпадений герба (цифры), определите вероятности выпадения герба (цифры). При оформлении сообщения с презентацией укажите цель работы, приборы и материалы, ход работы, вывод. Сопоставьте ваши результаты с выводами ученых, проводивших аналогичные опыты. Как вы думаете, зависят ли результаты от достоинства монеты и высоты стола? ИНТЕРНЕТ РЕСУРСЫ
Интернет ресурсы НАЗАД 1) Ахтямова Л. Т. «Предмет теории вероятностей. События. Вероятность события» . http: //festival. 1 september. ru/articles/569122/ Фестиваль педагогических идей «Открытый урок» 2) https: //ru. wikipedia. org/wiki/%D 2%E 5%EE%F 0%E 8%FF_%E 2%E 5%F 0%EE%FF%F 2%ED%EE%F 1%F 2%E 5%E 9 3) http: //www. mathprofi. ru/teorija_verojatnostei. html 4) http: //www. matburo. ru/ex_tv. php? p 1=tvklass 5) http: //www. toehelp. ru/theory/ter_ver/ 6) http: //www. math 10. com/ru/algebra/veroiatnosti/teoriya-veroyatnostei. html 7) https: //ru. wikipedia. org/wiki/%C 2%E 5%F 0%EE%FF%F 2%ED%EE%F 1%F 2%FC 8) http: //sernam. ru/book_tp. php? id=6 9) https: //ru. wikipedia. org/wiki/%D 0%98%D 1%81%D 1%82%D 0%BE%D 1%80%D 0%B 8%D 1%8 F_%D 1%82%D 0%B 5%D 0%BE%D 1%80%D 0%B 8_%D 0%B 2%D 0%B 5 %D 1%80%D 0%BE%D 1%8 F%D 1%82%D 0%BD%D 0%BE%D 1%81%D 1%82%D 0%B 5%D 0%B 9 10) http: //phizmat. org. ua/2009 -04 -21 -19 -42 -29/250 -2010 -05 -22 -19 -12 -15 11) http: //polit. ru/article/2014/03/30/lecture_bufetov/ 12) http: //www. bibliotekar. ru/100 otkr/47. htm 13) http: //infint. ru/zadachi-kavalera-de-mere/ 14) http: //www. km. ru/referats/134060 CE 3 E 8 D 4 ED 8 AD 57 A 017 FEB 26300 15) https: //ru. wikipedia. org/wiki/%C 8%E 3%F 0%EB%FC%ED%E 0%FF_%EA%EE%F 1%F 2%FC 16) http: //lingvomania. info/2010/chastye-bukvy. html 17) http: //spectator. ru/entry/1041 18) http: //ribalych. ru/2013/07/08/zanimatelnaya-podborka-faktov-o-russkom-yazyke/ 19) http: //www. speakrus. ru/articles/guinlang. htm 20) http: //orfogrammka. ru/%D 0%B 8%D 0%BD%D 1%82%D 0%B 5%D 1%80%D 0%B 5%D 1%81%D 0%BD%D 0%B 0%D 1%8 F_%D 1%84%D 0%B 8%D 0%BB%D 0%BE%D 0%BB%D 0 %BE%D 0%B 3%D 0%B 8%D 1%8 F/%D 0%B 8%D 0%BD%D 1%82%D 0%B 5%D 1%80%D 0%B 5%D 1%81%D 0%BD%D 1%8 B%D 0%B 5_%D 1%81%D 0%BB%D 0%BE%D 0%B 2% D 0%B 0_%D 1%80%D 1%83%D 1%81%D 0%BA%D 0%BE%D 0%B 3%D 0%BE_%D 1%8 F%D 0%B 7%D 1%8 B%D 0%BA%D 0%B 0/ 21) http: //nsportal. ru/ap/library/literaturnoe-tvorchestvo/2013/02/12/samaya-redkaya-bukva-russkogo-alfavita 22) http: //www. orenwiki. ru/index. php/%D 0%A 3%D 1%87%D 0%B 5%D 0%B 1%D 0%BD%D 0%BE%D 0%B 5_%D 0%B 8%D 1%81%D 0%BB%D 0%B 5%D 0%B 4%D 0%BE% D 0%B 2%D 0%B 0%D 0%BD%D 0%B 8%D 0%B 5_%D 0%B 2_%D 0%BF%D 1%80%D 0%BE%D 0%B 5%D 0%BA%D 1%82%D 0%B 5_%22%D 0%A 1%D 0%B 0%D 0%BC%D 0%B 0% D 1%8 F_%D 0%BD%D 0%B 5%D 0%BE%D 0%B 1%D 1%85%D 0%BE%D 0%B 4%D 0%B 8%D 0%BC%D 0%B 0%D 1%8 F_%D 0%B 1%D 1%83%D 0%BA%D 0%B 2%D 0%B 0_%D 0% B 2_%D 0%B 0%D 0%BB%D 1%84%D 0%B 0%D 0%B 2%D 0%B 8%D 1%82%D 0%B 5%22
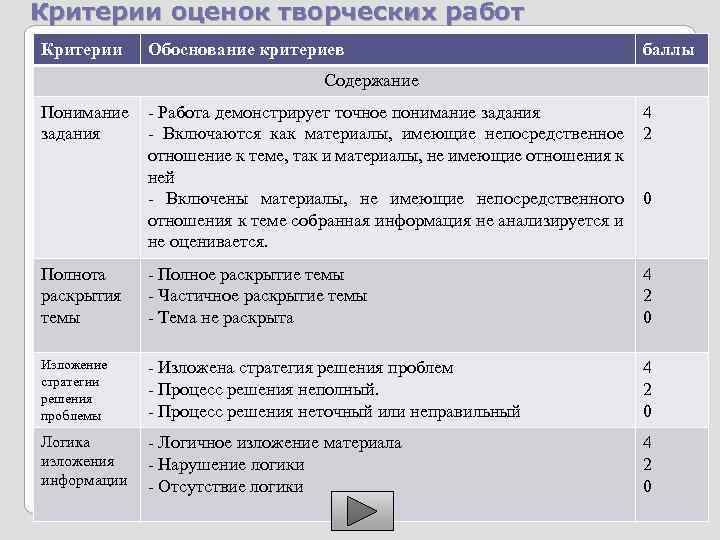
Критерии оценок творческих работ Критерии Обоснование критериев баллы Содержание Понимание задания - Работа демонстрирует точное понимание задания 4 - Включаются как материалы, имеющие непосредственное 2 отношение к теме, так и материалы, не имеющие отношения к ней - Включены материалы, не имеющие непосредственного 0 отношения к теме собранная информация не анализируется и не оценивается. Полнота раскрытия темы - Полное раскрытие темы - Частичное раскрытие темы - Тема не раскрыта 4 2 0 Изложение стратегии решения проблемы - Изложена стратегия решения проблем - Процесс решения неполный. - Процесс решения неточный или неправильный 4 2 0 Логика изложения информации - Логичное изложение материала - Нарушение логики - Отсутствие логики 4 2 0

Критерии оценок творческих работ Критерии Обоснование критериев баллы Самостоятельная работа группы Слаженная - Четко спланированная работа группы работа - Работа группы частично спланирована в группе - Не спланирована работа в группе 3 2 0 Распределе ние ролей в группе - Вся деятельность равномерно распределена между членами 3 команды - Работа над материалом равномерно распределена между 2 большинством участников команды - Несколько членов группы отвечают за работу всей команды. 0 Степень самостояте льности работы группы - Полная самостоятельность при выполнении работы - Частичная самостоятельность работы группы - Несамостоятельная работа группы 3 2 0
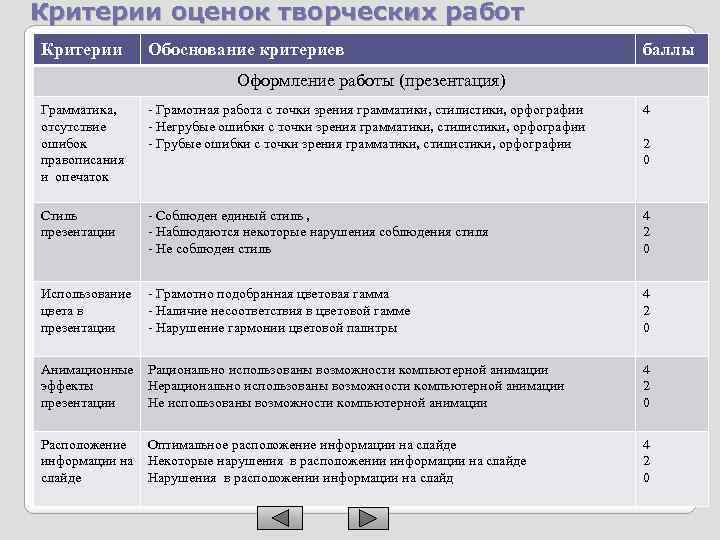
Критерии оценок творческих работ Критерии Обоснование критериев баллы Оформление работы (презентация) Грамматика, отсутствие ошибок правописания и опечаток - Грамотная работа с точки зрения грамматики, стилистики, орфографии - Негрубые ошибки с точки зрения грамматики, стилистики, орфографии - Грубые ошибки с точки зрения грамматики, стилистики, орфографии 4 Стиль презентации - Соблюден единый стиль , - Наблюдаются некоторые нарушения соблюдения стиля - Не соблюден стиль 4 2 0 Использование - Грамотно подобранная цветовая гамма цвета в - Наличие несоответствия в цветовой гамме презентации - Нарушение гармонии цветовой палитры 4 2 0 Анимационные Рационально использованы возможности компьютерной анимации эффекты Нерационально использованы возможности компьютерной анимации презентации Не использованы возможности компьютерной анимации 4 2 0 Расположение Оптимальное расположение информации на слайде информации на Некоторые нарушения в расположении информации на слайде Нарушения в расположении информации на слайд 4 2 0

Критерии оценок творческих работ Критерии назад Обоснование критериев баллы Защита работы Качество доклада - Аргументированность основных позиций, композиция доклада логична , полнота представления в докладе результатов работы - Нарушение логики выступления, неполное представление результатов работы, неполная система аргументации - Не заявлены аргументы по основным позициям , полное нарушение логики, не представлены результаты исследования 4 - Докладчики демонстрируют эрудицию, отражают межпредметные связи - Докладчики грамотно излагают материал, но не показывают достаточно глубоких знаний -Докладчики обнаруживают полное невладение материалом 4 2 0 Культура речи, манера держаться перед аудиторией - Докладчики уверенно держатся перед аудиторией, грамотно владеют речью, соблюдают регламент, удерживают внимание аудитории - Докладчики допускают негрубые речевые ошибки при выступлении, незначительно нарушают регламент, частично удерживают внимание аудитории - Докладчики теряются перед аудиторией, обнаруживают бедность речи, нарушают регламент, не могут удержать внимание аудитории 4 2 0 Ответы на вопросы - Докладчики убедительно и полно отвечают на вопросы, дружелюбно держатся, стремятся использовать ответы для успешного раскрытия темы. - Докладчик не на все вопросы может найти убедительные ответы - Докладчик не может ответить на вопросы или при ответах ведет себя агрессивно, некорректно 4 2 0 Деловые и волевые качества докладчика - Докладчик стремится к достижению высоких результатов, готов к дискуссии, доброжелателен, контактен - Докладчик готов к дискуссии, не всегда проявляет доброжелательность - Докладчик не готов к дискуссии, агрессивен, уходит от контактов 4 2 0 Объем и знаний по теме глубина 2 0

1. Предварительно оцените себя, используя раздел «Критерии оценок» . 2. Оформите решение творческой работы или задач своей группы в виде презентации. 3. Обсудите результаты работы, проведите защиту презентации. 4. Решите задачи Критерии оценки творческих работ Итоги Критерии оценки решения задач Задачи для самостоятельног о решения
Задания для группы историков Задания для группы теоретиков Задания для группы практиков назад Задания для группы исследователей Задания для группы экспериментаторов Задачи для самостоятельного решения: Критерии оценки решения задач

Задача 1. Определите вид события (достоверное, невозможное, случайное): А – «из 30 студентов группы двое справляют день рождения 30 января» . Задача 2. Являются ли несовместными события, если испытание – сыгранная партия в шахматы; события: А 1 – «Катя выиграла» , А 2 – «Слава проиграл» ? Задача 3. Являются ли равновозможными события, если испытание – бросание двух монет; события: А 1 – «выпадет только один герб» , А 2– «выпадут два герба» ? Задача 4. В коробке 3 кубика: черный (ч), красный (к), синий (с). Вытаскивая кубики наугад, ставим их последовательно один за другим. Какова вероятность того, что в результате появится последовательность кубиков «ч, к, с» ? Задача 5. Бросаются две игральные кости: белая и красная. Какова вероятность выпадения дубля? Дублем называют совпадение числа очков, выпавших на каждой кости. Задача 6. На карточках написали цифры 1; 2; 3, после чего карточки перевернули и перемешали. Затем последовательно открыли и положили в ряд. Какова вероятность того, что получится трёхзначное число, меньшее 200? назад Задания для группы историков
Задача 1. Определите вид события (достоверное, невозможное, случайное): А – «при бросании двух игральных костей на одной выпадет 3 очка, а на другой – 5 очков» . Задача 2. Являются ли несовместными события, если испытание – бросание двух монет; события: А 1 – «появление герба на одной из монет» , А 2– «появление герба на другой монете» ? Задача 3. Являются ли равновозможными события, если испытание – выбор наугад одной карты; события: А 1– «вынута карта красной масти» , А 2– «вынута карта пиковой масти» ? Задача 4. На карточках написали цифры 1; 2; 3, после чего карточки перевернули и перемешали. Затем последовательно открыли и положили в ряд. Какова вероятность того, что получится трёхзначное число, большее 300? Задача 5. У маленькой Вари были две одинаковые пары варежек, но одну из варежек она потеряла. Уходя на улицу, она наугад берет две варежки. Какова вероятность того, что они окажутся парными (т. е. на разные руки)? Задача 6. В мешке содержится 24 шара, среди которых белых шаров в 2 раза больше, чем черных, а остальные шары – красные. Вероятность того, что вынутый шар окажется черным, равна 1/8. Какова вероятность того, что вынутый шар окажется красным? назад Задания для группы теоретиков

Задача 1. Случайным образом открывается учебник литературы и находится второе слово на левой странице. Определите вид события (достоверное, невозможное, случайное): А – «это слово начинается с буквы “к”» . Задача 2. Являются ли несовместными события, если испытание – выбор из группы наугад одного студента; события: А 1– «это юноша» , А 2– «этот студент живет в общежитии» ? Задача 3. Являются ли равновозможными события, если испытание – два выстрела по мишени; события: А 1– «промах при первом выстреле» , А 2– «промах при втором выстреле» ? Задача 4. Брошены 2 игральные кости. Какова вероятность того, что в сумме выпадет не более 9 очков? Задача 5. Набирая семизначный номер телефона, абонент забыл в какой последовательности идут три последние цифры. Помня лишь что, это цифры 1; 5; 9; он набрал первые 4 цифры, которые знал, и наугад комбинацию из цифр 1; 5; 9. Какова вероятность, что абонент наберет верный номер? Задача 6. Для экзамена подготовлено 25 билетов. Какова вероятность того, что взятый наугад студентом билет имеет однозначный номер? назад Задания для группы практиков

Задача 1. Определите вид события (достоверное, невозможное, случайное): – «при нормальном атмосферном давлении в Уфе вода закипит при t=80 » Задача 2. Являются ли несовместными события, если испытание – два выстрела по мишени; события: А 1– «есть хотя бы одно попадание» , А 2– «ни одного попадания» ? Задача 3. Являются ли равновозможными события, если испытание – бросание игральной кости; события: А 1– «появление двух очков» , А 2– «появление пяти очков» ? Задача 4. Какова вероятность того, что при бросании игрального кубика выпадет не менее 3 очков? Задача 5. На карточках написали цифры 1; 2; 3, после чего карточки перевернули и перемешали. Затем последовательно открыли и положили в ряд. Какова вероятность того, что получится трёхзначное число, первая цифра которого 2? Задача 6. В мешке содержится 12 шаров, среди которых белых в 2 раза больше, чем черных. Какова вероятность того, что вынутый наугад шар будет белым? назад Задания для группы исследователей

Задача 1. Определите вид события (достоверное, невозможное, случайное): А – «в сыгранной Катей и Славой партии в шахматы Катя выиграла, а Слава проиграл» . Задача 2. Являются ли несовместными события, если испытание – выбор из группы наугад одного студента; события: А 1– «это девушка» , А 2– «имя студента – Женя» ? Задача 3. Являются ли равновозможными события, если испытание – бросание игральной кости; события: А 1– «появление двух очков» , А 2– «появление четного числа очков» ? Задача 4. Брошены две игральные кости: белая и красная. Какова вероятность того, что сумма выпавших очков равна 10? Задача 5. Из 25 экзаменационных билетов студент успел подготовить 11 первых и 8 последних билетов. Какова вероятность того, что на экзамене ему достанется билет, который он не подготовил? Задача 6. Монета брошена два раза. Какова вероятность того, что хотя бы один раз выпадет герб? назад Задания для группы экспериментаторов
назад ОБРАЗЕЦ Решение задач по схеме ОБРАЗЕЦ Оформление решения задач ОБЪЯСНИ Решение задач Примеры решения задач

1. Внимательно прочитайте задачу, выясните, что именно происходит, т. е. опишите опыт (испытание). 2. Найдите основной вопрос задачи: «Вычислить (найти) вероятность того, что…» . 3. Введите событие А, вероятность которого нужно найти. 4. Определите общее число всех элементарных равновозможных несовместных исходов – n. 5. Определите число исходов, благоприятных событию А – m. 6. Составьте отношение m к n. 7. Найдите значение отношения – Р(А). 8. Запишите ответ. Схема решения задач на применение формулы вероятности:

Решение задач по схеме. Пример 1 Схема решения задачи Исследование содержания задачи 1. Внимательно прочитайте задачу, выясните, что именно происходит, т. е. опишите опыт (испытание). В коробке 3 черных и 4 белых шара. Из нее наугад вынимают один шар. Найдите вероятность того, что шар будет черным. 2. Найдите основной вопрос задачи: «Вычислить (найти) вероятность того, что…» Найдите вероятность того, что шар будет черным. 3. Введите событие А, вероятность которого нужно найти. А - «шар будет черным» . 4. Определите общее число всех элементарных Всего шаров в коробке: 3 + 4 = 7, п=7. равновозможных несовместных исходов – n. 5. Определите число исходов, благоприятных событию А – m. Всего черных шаров – 3, m = 3 6. Составьте отношение m к n. 3/7 7. Найдите значение отношения – Р(А) =3/7 8. Ответ: Р(А) =3/7.

Решение задач по схеме. Пример 2 Схема решения задачи Исследование содержания задачи 1. Внимательно прочитайте задачу, выясните, что именно происходит, т. е. опишите опыт (испытание). На полке стоят 3 синих, 2 зеленых, 5 красных книги. Вычислите вероятность того, что Вера возьмет с полки красную книгу. 2. Найдите основной вопрос задачи: «Вычислить (найти) вероятность того, что…» Вычислите вероятность того, что Вера возьмет с полки красную книгу. 3. Введите событие А, вероятность которого нужно найти. А - «Вера возьмет с полки красную книгу» . 4. Определите общее число всех элементарных Всего книг на полке: 3 + 2 + 5 = 10, n = 10 равновозможных несовместных исходов – n. 5. Определите число исходов, благоприятных событию А – m. Всего красных книг на полке – 5, m = 5 6. Составьте отношение m к n. 5/10=1/2=0, 5 7. Найдите значение отношения – Р(А) = 0, 5 8. Ответ: Р(А) = 0, 5
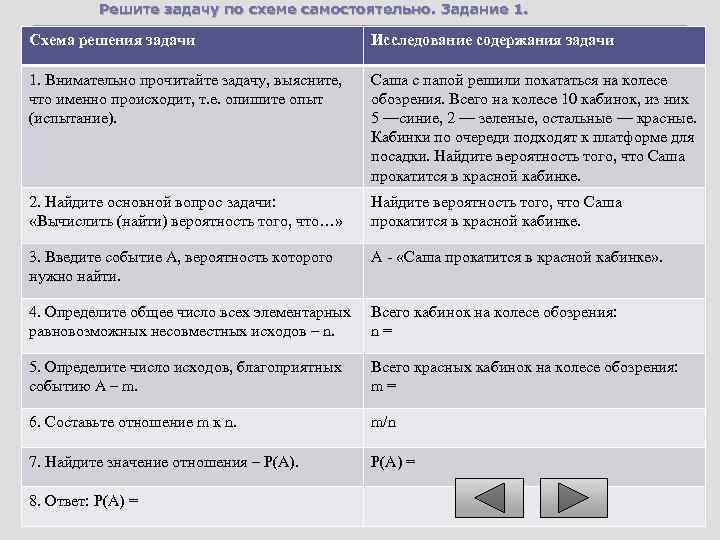
Решите задачу по схеме самостоятельно. Задание 1. Схема решения задачи Исследование содержания задачи 1. Внимательно прочитайте задачу, выясните, что именно происходит, т. е. опишите опыт (испытание). Саша с папой решили покататься на колесе обозрения. Всего на колесе 10 кабинок, из них 5 —синие, 2 — зеленые, остальные — красные. Кабинки по очереди подходят к платформе для посадки. Найдите вероятность того, что Саша прокатится в красной кабинке. 2. Найдите основной вопрос задачи: «Вычислить (найти) вероятность того, что…» Найдите вероятность того, что Саша прокатится в красной кабинке. 3. Введите событие А, вероятность которого нужно найти. А - «Саша прокатится в красной кабинке» . 4. Определите общее число всех элементарных Всего кабинок на колесе обозрения: равновозможных несовместных исходов – n. n = 5. Определите число исходов, благоприятных событию А – m. Всего красных кабинок на колесе обозрения: m = 6. Составьте отношение m к n. m/n 7. Найдите значение отношения – Р(А) = 8. Ответ: Р(А) =
Решите задачу по схеме самостоятельно. Задание 1. (проверка) Схема решения задачи Исследование содержания задачи 1. Внимательно прочитайте задачу, выясните, что именно происходит, т. е. опишите опыт (испытание). Саша с папой решили покататься на колесе обозрения. Всего на колесе 10 кабинок, из них 5 —синие, 2 — зеленые, остальные — красные. Кабинки по очереди подходят к платформе для посадки. Найдите вероятность того, что Саша прокатится в красной кабинке. 2. Найдите основной вопрос задачи: «Вычислить (найти) вероятность того, что…» Найдите вероятность того, что Саша прокатится в красной кабинке. 3. Введите событие А, вероятность которого нужно найти. А - «Саша прокатится в красной кабинке» . 4. Определите общее число всех элементарных Всего кабинок на колесе обозрения: равновозможных несовместных исходов – n. n =10 5. Определите число исходов, благоприятных событию А – m. Всего красных кабинок на колесе обозрения: m = 3 6. Составьте отношение m к n. 3/10 7. Найдите значение отношения – Р(А) =0, 3 8. Ответ: Р(А) = 0, 3 назад

Пример № 1 Коля, Ваня, Петя, Вася бросили жребий – кому идти в магазин. Найдите вероятность того, что в магазин пойдет Петя. Решение: Обозначим событие А – «в магазин пойдет Петя» . Тогда общее число всех возможных исходов: n = 4 (всего мальчиков). Число благоприятных исходов: m = 1 (жребий выпал на Петю). Вероятность Р(А) = m/n =1/4 = 0, 25. Ответ: 0, 25. назад Оформление решения задач
Объясни задачи 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что герб выпадет все три раза. В случайном эксперименте бросают два игральных кубика. Найдите вероятность того, что в сумме выпадет 8 очков. Алексей наудачу выбирает двузначное число. Найдите вероятность того, что оно оканчивается на 0. Какова вероятность того, что при бросании игрального кубика выпадет число очков больше 4? В чемпионате мира участвуют 25 команд. С помощью жребия их нужно разделить на пять групп по пять команд в каждой. В ящике вперемешку лежат карточки с номерами групп: 1, 1, 1, 2, 2, 2, 3, 3, 3, 4, 4, 4, 5, 5, 5. Капитаны команд тянут по одной карточке. Какова вероятность того, что команда Франции окажется в первой группе? В соревнованиях по толканию ядра участвуют 9 спортсменов из Дании, 3 спортсмена из Швеции, 8 спортсменов из Норвегии и 5 – из Финляндии. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, который выступает последним, окажется из Финляндии. На семинар приехали трое ученых из Норвегии, четверо из России и трое из Испании. Порядок докладов определяется жеребьёвкой. Найдите вероятность того, что восьмым окажется доклад ученого из России. Телевизор у Марины сломался и показывает только один случайный канал. Марина включает телевизор. В это время по шести каналам из тридцати девяти показывают новости. Найдите вероятность того, что Марина попадет на канал, где новости не идут. Тринадцать студентов 1 курса пришли на занятия в костюмах, четверо - в футболках, пятеро - в свитерах, трое – в рубашках. Какова вероятность того, что случайно выбранный студент 1 курса пришел на занятия в футболке? В фирме такси в данный момент свободно 20 машин: 2 черных, 5 желтых и 13 зеленых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет желтое такси. назад
Количество верных ответов Результат 6 верных ответов Вы отлично усвоили тему 5 верных ответа Будьте внимательнее, вы просто торопитесь 4 - 3 верных ответа Возможно вам необходимо вспомнить теорию 1 - 2 верных ответа Изучите внимательно тему еще раз Критерии оценок по решению задач назад
квест по теории вероятностей.pptx