 Вдохновение нужно в геометрии не меньше, чем в поэзии. А. С. Пушкин
Вдохновение нужно в геометрии не меньше, чем в поэзии. А. С. Пушкин
 План урока & Проверка домашнего задания & Геометрический диктант & Применение изучаемого материала & Изучение нового материала & Тест & Домашнее задание
План урока & Проверка домашнего задания & Геометрический диктант & Применение изучаемого материала & Изучение нового материала & Тест & Домашнее задание
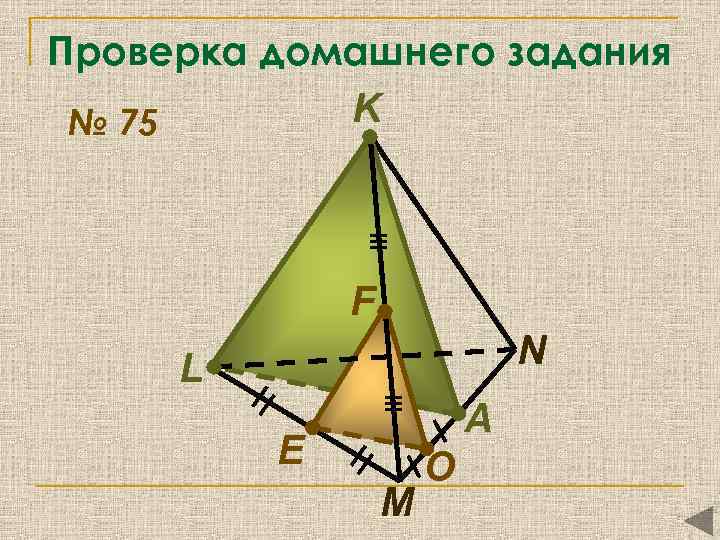 Проверка домашнего задания K № 75 F N L A E M O
Проверка домашнего задания K № 75 F N L A E M O
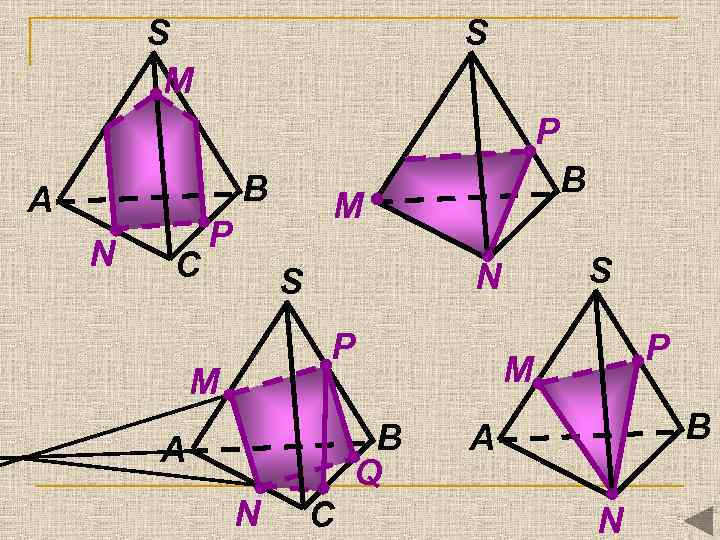 S M S P B А N С B M P P M B Q А N S С P M B А N
S M S P B А N С B M P P M B Q А N S С P M B А N
 Геометрический диктант
Геометрический диктант
 В строительстве и архитектуре
В строительстве и архитектуре
 В медицине
В медицине
 В археологии и истории
В археологии и истории
 В ювелирном искусстве
В ювелирном искусстве
 Построение сечений в параллелепипеде: · По трем точкам, лежащим на трех соседних ребрах. ¸ По трем точкам, лежащим на трех параллельных ребрах (Случай 1). ¹ По трем точкам, лежащим на трех параллельных ребрах (Случай 2). º По трем точкам, не лежащим на трех параллельных ребрах (Случай 1). » По трем точкам, не лежащим на трех параллельных ребрах (Случай 2).
Построение сечений в параллелепипеде: · По трем точкам, лежащим на трех соседних ребрах. ¸ По трем точкам, лежащим на трех параллельных ребрах (Случай 1). ¹ По трем точкам, лежащим на трех параллельных ребрах (Случай 2). º По трем точкам, не лежащим на трех параллельных ребрах (Случай 1). » По трем точкам, не лежащим на трех параллельных ребрах (Случай 2).
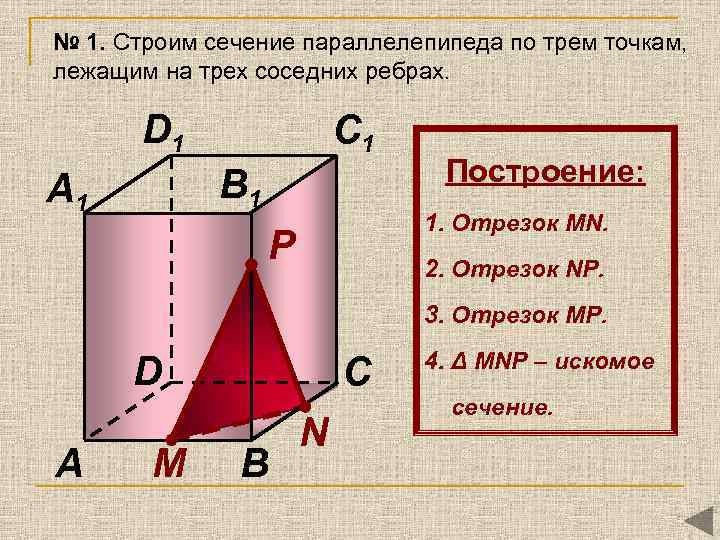 № 1. Строим сечение параллелепипеда по трем точкам, лежащим на трех соседних ребрах. D 1 C 1 B 1 A 1 Построение: 1. Отрезок MN. P 2. Отрезок NР. 3. Отрезок MР. D A М C B N 4. Δ MNР – искомое сечение.
№ 1. Строим сечение параллелепипеда по трем точкам, лежащим на трех соседних ребрах. D 1 C 1 B 1 A 1 Построение: 1. Отрезок MN. P 2. Отрезок NР. 3. Отрезок MР. D A М C B N 4. Δ MNР – искомое сечение.
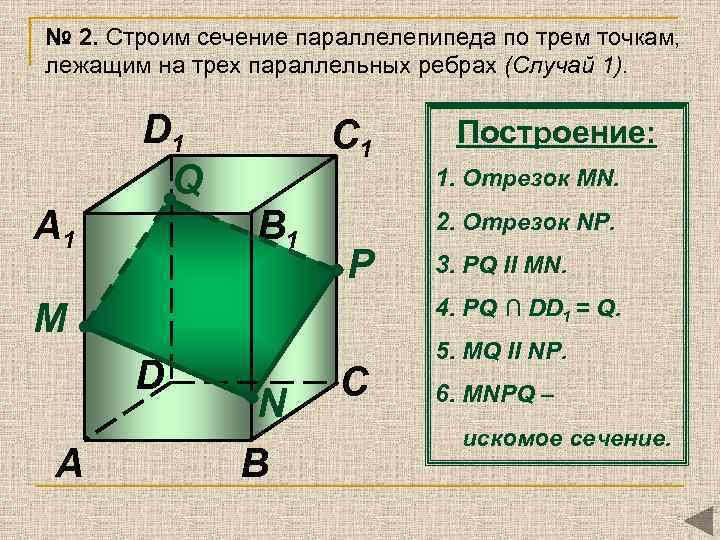 № 2. Строим сечение параллелепипеда по трем точкам, лежащим на трех параллельных ребрах (Случай 1). D 1 Q A 1 C 1 1. Отрезок MN. B 1 2. Отрезок NР. P 3. РQ II MN. 4. PQ ∩ DD 1 = Q. М D A Построение: N B C 5. MQ II NP. 6. MNРQ – искомое сечение.
№ 2. Строим сечение параллелепипеда по трем точкам, лежащим на трех параллельных ребрах (Случай 1). D 1 Q A 1 C 1 1. Отрезок MN. B 1 2. Отрезок NР. P 3. РQ II MN. 4. PQ ∩ DD 1 = Q. М D A Построение: N B C 5. MQ II NP. 6. MNРQ – искомое сечение.
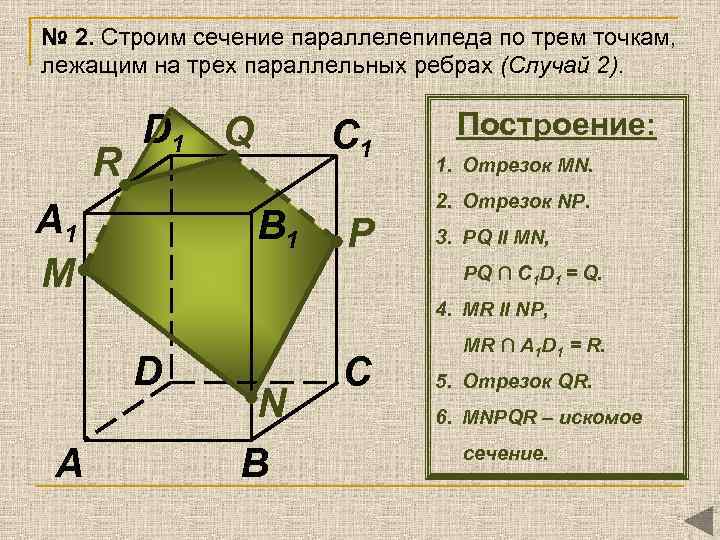 № 2. Строим сечение параллелепипеда по трем точкам, лежащим на трех параллельных ребрах (Случай 2). R D 1 Q A 1 М C 1 B 1 P Построение: 1. Отрезок MN. 2. Отрезок NР. 3. РQ II MN, PQ ∩ C 1 D 1 = Q. 4. MR II NP, D A N B C MR ∩ A 1 D 1 = R. 5. Отрезок QR. 6. MNРQR – искомое сечение.
№ 2. Строим сечение параллелепипеда по трем точкам, лежащим на трех параллельных ребрах (Случай 2). R D 1 Q A 1 М C 1 B 1 P Построение: 1. Отрезок MN. 2. Отрезок NР. 3. РQ II MN, PQ ∩ C 1 D 1 = Q. 4. MR II NP, D A N B C MR ∩ A 1 D 1 = R. 5. Отрезок QR. 6. MNРQR – искомое сечение.
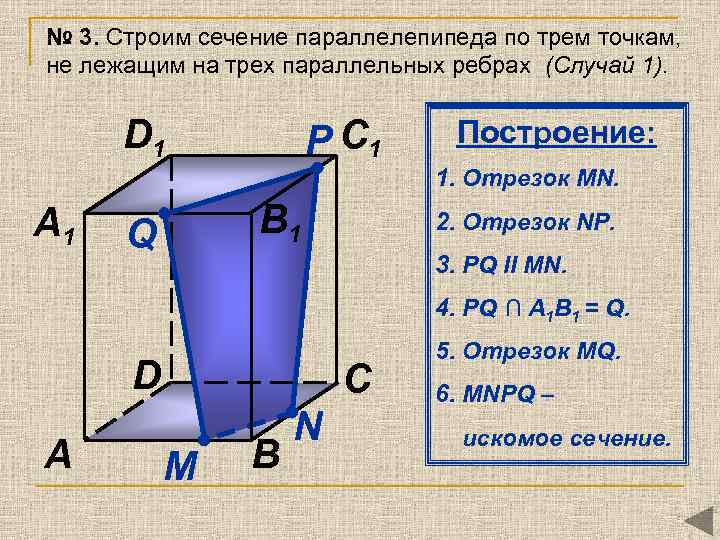 № 3. Строим сечение параллелепипеда по трем точкам, не лежащим на трех параллельных ребрах (Случай 1). D 1 P C 1 Построение: 1. Отрезок MN. A 1 B 1 Q 2. Отрезок NР. 3. РQ II MN. 4. PQ ∩ А 1 В 1 = Q. D A C М B N 5. Отрезок MQ. 6. MNРQ – искомое сечение.
№ 3. Строим сечение параллелепипеда по трем точкам, не лежащим на трех параллельных ребрах (Случай 1). D 1 P C 1 Построение: 1. Отрезок MN. A 1 B 1 Q 2. Отрезок NР. 3. РQ II MN. 4. PQ ∩ А 1 В 1 = Q. D A C М B N 5. Отрезок MQ. 6. MNРQ – искомое сечение.
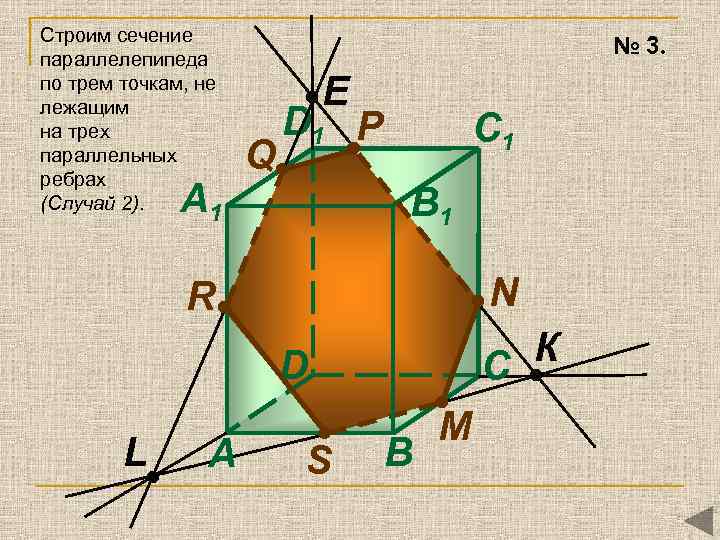 Строим сечение параллелепипеда по трем точкам, не лежащим на трех параллельных ребрах (Случай 2). A 1 № 3. E Q D 1 P C 1 B 1 N R К C D L A S B М
Строим сечение параллелепипеда по трем точкам, не лежащим на трех параллельных ребрах (Случай 2). A 1 № 3. E Q D 1 P C 1 B 1 N R К C D L A S B М
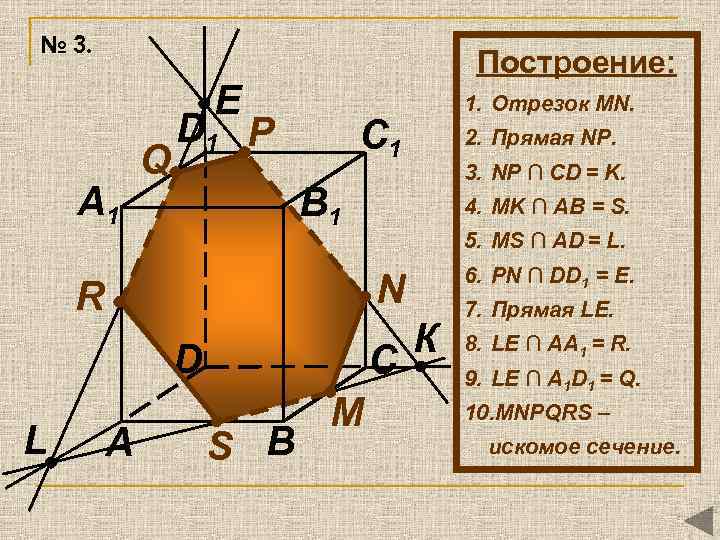 № 3. Построение: E A 1 Q D 1 P C 1 2. Прямая NР. 3. NP ∩ CD = K. B 1 4. MK ∩ AB = S. 5. MS ∩ AD = L. 6. PN ∩ DD 1 = E. N R D L 1. Отрезок MN. A C S B М К 7. Прямая LE. 8. LE ∩ AA 1 = R. 9. LE ∩ A 1 D 1 = Q. 10. MNРQRS – искомое сечение.
№ 3. Построение: E A 1 Q D 1 P C 1 2. Прямая NР. 3. NP ∩ CD = K. B 1 4. MK ∩ AB = S. 5. MS ∩ AD = L. 6. PN ∩ DD 1 = E. N R D L 1. Отрезок MN. A C S B М К 7. Прямая LE. 8. LE ∩ AA 1 = R. 9. LE ∩ A 1 D 1 = Q. 10. MNРQRS – искомое сечение.
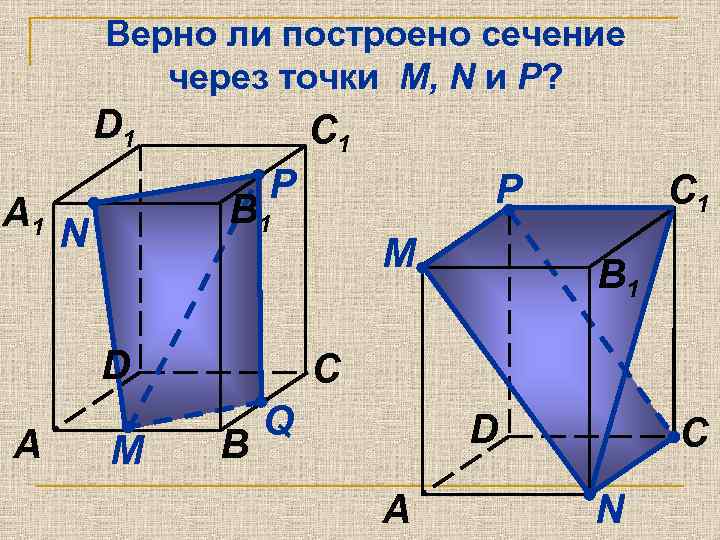 Верно ли построено сечение через точки M, N и P? D 1 A 1 C 1 P B 1 N D A P М М C 1 B 1 C B Q D A C N
Верно ли построено сечение через точки M, N и P? D 1 A 1 C 1 P B 1 N D A P М М C 1 B 1 C B Q D A C N