Василий Васильевич Леонтьев и его модель Межотраслевого баланса Подготовила: Козлова Анна, МО, 4 курс
Биография Васильевича Леонтьева Родился 5 августа 1905 года в Санкт – Петербурге. Родители: Василий Леонтьев и Евгения Беккер. В 1921 г. поступил в Ленинградский университет. Разработал теоретические основы межотраслевого баланса в СССР в 19231924 гг.
В возрасте 22 лет он получил степень доктора наук по экономике. В 1931 г. эмигрировал в США, где поступил на работу в Национальное бюро по экономическим исследова ниям. В 1946 г. он стал про фессором в Гарвардском университете.
Леонтьев был удостоен Премии памяти Нобеля по экономике в 1973 г. "за развитие метода "затраты – выпуск" и за его применение к важным экономическим проблемам". Был возведен в звание офицера Почетного легиона Франции. Член американской Национальной академии наук, Американской академии наук и искусств. Британской академии и Королевского статистического общества в Лондоне. Он занимал пост президента Эконометрического общества в 1954 г. и Американской экономической ассоциации в 1970 г.
Межотраслевой баланс. Определение Межотраслевой баланс (МОБ, метод «затраты-выпуск» ) — экономико-математическая балансовая модель, характеризующая межотраслевые производственные взаимосвязи в экономике страны.
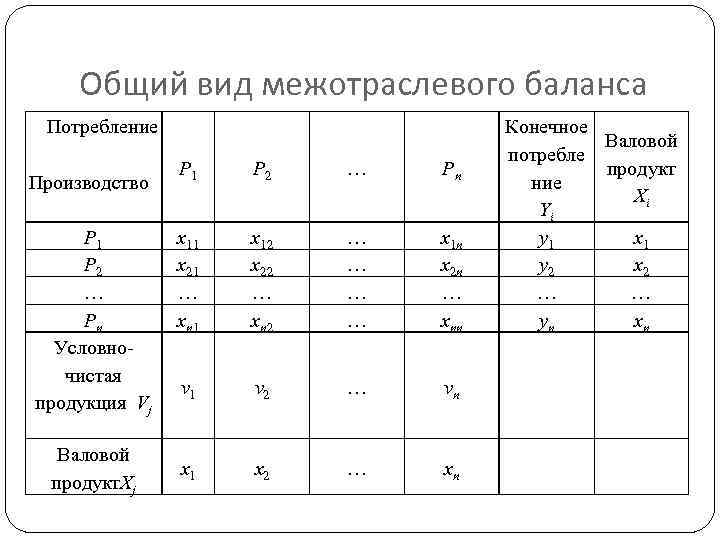
Общий вид межотраслевого баланса Потребление Производство P 1 P 2 … Pn Условночистая продукция Vj Валовой продукт. Xj P 1 P 2 … Pn x 11 x 21 … xn 1 x 12 x 22 … xn 2 … … x 1 n x 2 n … xnn v 1 v 2 … vn x 1 x 2 … xn Конечное Валовой потребле продукт ние Xi Yi y 1 x 1 y 2 x 2 … … yn xn
Введем следующие показатели xij - затраты продукта i-й отрасли на производственные нужды j-й отрасли; xi – валовой продукт i-й отрасли; yi – конечный продукт (конечное потребление) i-й отрасли; vj – условно-чистая продукция j-й отрасли за некоторый промежуток времени (год, квартал и т. д. )
Система уравнений соотношение баланса между производством и потреблением: xi= +yi (1) стоимостная структура продукта каждой отрасли: xj= +vj (2) суммарный конечный продукт равен суммарной условно-чистой продукции: (3)
Математическая модель Соотношение xij=aijxj (4) выражает условие линейной зависимости объема производства от издержек или линейности существующей технологии. • Коэффициенты (5) где называют коэффициентами прямых материальных затрат или технологическими коэффициентами. Матрицу , называют матрицей прямых материальных затрат.
Линейная балансовая модель (6) или в матричной форме: (7) А – матрица коэффициентов прямых материальных затрат, Е – единичная матрица порядка n, - вектор конечного потребления, - вектор валового выпуска.
Скачать презентацию Василий Васильевич Леонтьев и его модель Межотраслевого баланса
В.В.Леонтьев.pptx