ВАРИАЦИЯ ПРИЗНАКОВ 1 ВАРИАЦИЯ КОЛИЧЕСТВЕННОГО ПРИЗНАКА 2 ПРИМЕНЕНИЕ

ВАРИАЦИЯ ПРИЗНАКОВ 1. ВАРИАЦИЯ КОЛИЧЕСТВЕННОГО ПРИЗНАКА 2. ПРИМЕНЕНИЕ ПОКАЗАТЕЛЕЙ ВАРИАЦИИ ДЛЯ ОЦЕНКИ ФОРМЫ РАСПРЕДЕЛЕНИЯ ДАННЫХ 3. ДИСПЕРСИЯ АЛЬТЕРНАТИВНОГО ПРИЗНАКА 4. ЗАКОН СЛОЖЕНИЯ ДИСПЕРСИЙ

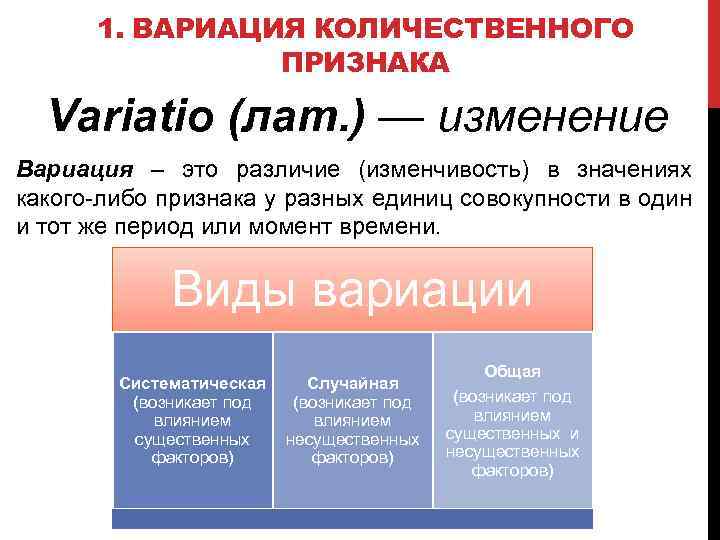1. ВАРИАЦИЯ КОЛИЧЕСТВЕННОГО ПРИЗНАКА Variatio (лат. ) — изменение Вариация – это различие (изменчивость) в значениях какого-либо признака у разных единиц совокупности в один и тот же период или момент времени. Виды вариации Систематическая (возникает под влиянием существенных факторов) Случайная (возникает под влиянием несущественных факторов) Общая (возникает под влиянием существенных и несущественных факторов)

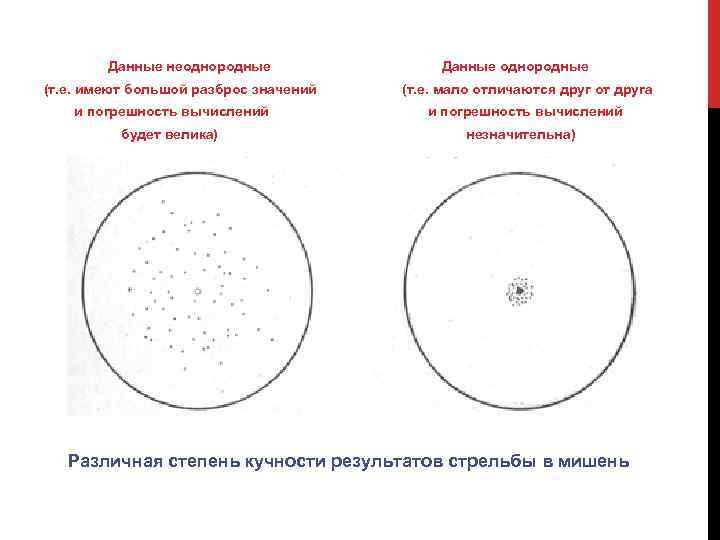Данные неоднородные (т. е. имеют большой разброс значений и погрешность вычислений будет велика) Данные однородные (т. е. мало отличаются друг от друга и погрешность вычислений незначительна) Различная степень кучности результатов стрельбы в мишень

ФОРМУЛЫ РАСЧЕТА ПОКАЗАТЕЛЕЙ ВАРИАЦИИ № Показатель вариации п/п Формула расчета Характеристика показателя Абсолютные показатели 1. Размах вариации R = xmax – xmin 2. Среднее отклонение линейное простое а) Характеризует диапазон рассеивания значений признака Х от минимального до максимального значений или амплитуду колебаний Характеризует абсолютное отклонение значений признака Х от средней величины б) взвешенное 3. Общая дисперсия или а) простая средний квадрат отклонений Характеризует площадь рассеивания значений признака Х вокруг средней величины Формулу простой дисперсии можно преобразовать следующим образом: б) взвешенная 4. Среднее квадратическое (стандартное) отклонение Характеризует отклонение значений признака Х в обе стороны от средней величины

ФОРМУЛЫ РАСЧЕТА ПОКАЗАТЕЛЕЙ ВАРИАЦИИ № Показатель вариации п/п 5. Коэффициент осцилляции 6. Относительное отклонение 7. Коэффициент вариации Формула расчета Характеристика показателя Относительные показатели Характеризует относительную рассеянность или колеблемость крайних значений признака вокруг средней, т. е. показывает, на сколько процентов отклоняется среднее значение от крайних значений вариации Характеризует абсолютное отклонение значений признака от средней величины в процентах Характеризует степень отклонения значений признака от средней величины в процентах. Если V ≤ 33%, то вариация значений признака считается несущественной, а данные однородными. Если 33 < V ≤ 66%, то степень вариации считается средней, данные можно использовать в исследованиях, но необходимо учитывать возникающую погрешность вычислений. Если V > 66%, то вариация значений признака велика и такие данные в расчетах не используются.

В зарубежной литературе такие показатели, как минимум, максимум, среднее значение, дисперсия, стандартное отклонение, медиана, мода и т. д. называются описательными или дескриптивными статистиками. Вместо того чтобы рассматривать все значения переменной, а их может быть очень много (тысячи и миллионы), вначале стоит просмотреть описательные статистики. Они дают общее представление о значениях, которые принимает переменная.

2. ПРИМЕНЕНИЕ ПОКАЗАТЕЛЕЙ ВАРИАЦИИ ДЛЯ ОЦЕНКИ ФОРМЫ РАСПРЕДЕЛЕНИЯ ДАННЫХ Средние величины и показатели вариации представляют собой частные случаи единой системы статистических характеристик распределения данных, т. е. системы моментов распределения, разработанной русским математиком П. Л. Чебышевым Общая формула центральных моментов k-го порядка имеет вид: 1. Центральный момент нулевого порядка всегда равен единице: 2. Центральный момент первого порядка всегда равен нулю:

3. Центральный момент второго порядка представляет собой дисперсию данного распределения: 4. Центральный момент третьего порядка используется для характеристики асимметрии распределения: Для этого определяют моментный коэффициент асимметрии: Если As < 0, то имеет место левосторонняя (отрицательная) асимметрия. Если As > 0, то имеет место правосторонняя (положительная) асимметрия. Если |As| < 0, 5, то асимметрия считается несущественной.

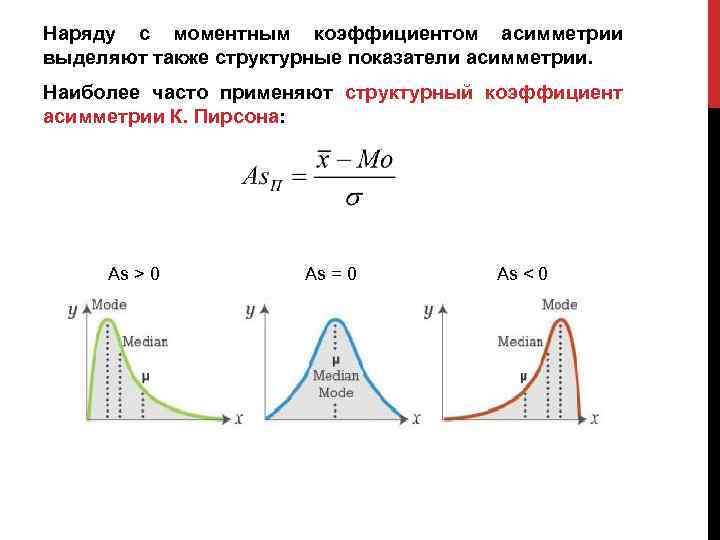Наряду с моментным коэффициентом асимметрии выделяют также структурные показатели асимметрии. Наиболее часто применяют структурный коэффициент асимметрии К. Пирсона: As > 0 As = 0 As < 0

5. Центральный момент четвертого порядка: На основе центрального момента четвертого порядка определяется эксцесс, который показывает отклонение вершины данного распределения вверх или вниз от вершины кривой нормального распределения: Если Ex = 0, то распределение нормальное. Если Ex > 0, то распределение островершинное. Если Ex < 0, то распределение плосковершинное.

3. ДИСПЕРСИЯ АЛЬТЕРНАТИВНОГО ПРИЗНАКА Вариация альтернативных признаков заключается в том, что у одних единиц совокупности нужное значение признака наблюдаются, а у других нет! Наличие признака обозначим как 1, а его отсутствие – 0, тогда доля единиц, обладающих признаком, обозначается p, а доля единиц, не обладающих данным признаком – q, тогда p + q = 1, отсюда: Дисперсия альтернативного признака равна: Она не может принимать значений больше 0, 25, т. к. 0, 5 х 0, 5 = 0, 25. Пример. Определить дисперсию, если среди партии деталей оказалось 2% бракованных изделий р = 0, 02, тогда q = 0, 98, отсюда 0, 02 х 0, 98 = 0, 0196

4. ЗАКОН СЛОЖЕНИЯ ДИСПЕРСИЙ В статистической практике правило сложения дисперсий используется при определении тесноты связи между факторным и результативным признаками. Общее правило (закон) сложения дисперсий: где – общая дисперсия; – межгрупповая дисперсия; – средняя из внутригрупповых дисперсий (частных дисперсий)

Межгрупповая дисперсия показывает силу влияния группировочного признака на величину вариации изучаемого явления: Частные (внутригрупповые) дисперсии отражают силу влияния всех неучтенных факторов на величину изучаемого явления: где - групповые средние.

Пользуясь правилом сложения дисперсий, можно судить о силе влияния группировочного признака на величину вариации изучаемого явления: чем больше доля межгрупповой дисперсии в общей дисперсии, тем сильнее влияние группировочного признака на изучаемое явление. Долю межгрупповой дисперсии в общей отражает эмпирический коэффициент детерминации: