Вариационные ряды Средние величины Корреляционный анализ Вариационный

Вариационные ряды Средние величины Корреляционный анализ

Вариационный ряд числовые значения признака, представленные в ранговом порядке с соответствующими этим значениям частотами

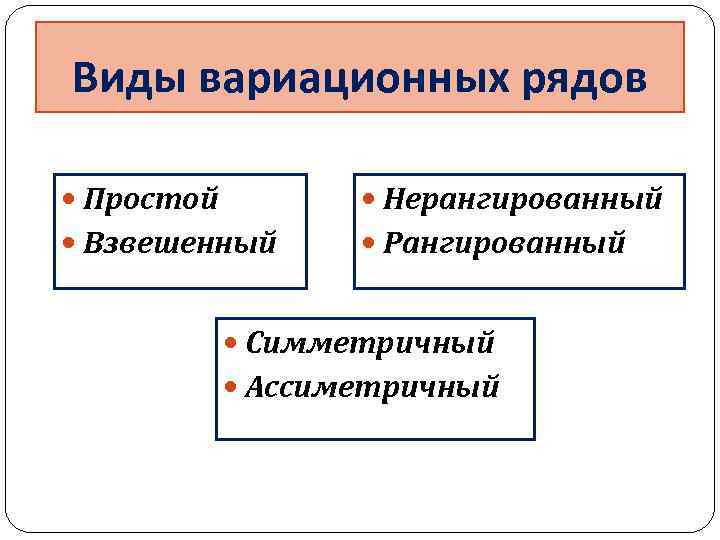Виды вариационных рядов Простой Нерангированный Взвешенный Рангированный Симметричный Ассиметричный

Элементы вариационного ряда V варианта, отдельное числовое выражение изучаемого признака p n частота (“вес”) общее число варианты, наблюдений число ее повторений в вариационном ряду

Критерии разнообразия признака Vmax и Vmin — крайние варианты, граничивающие вариационный ряд А — амплитуда ряда Lim – лимит вариационного ряда σ ( «сигма» ) —среднеквадратическое отклонение СV - коэффициент вариации

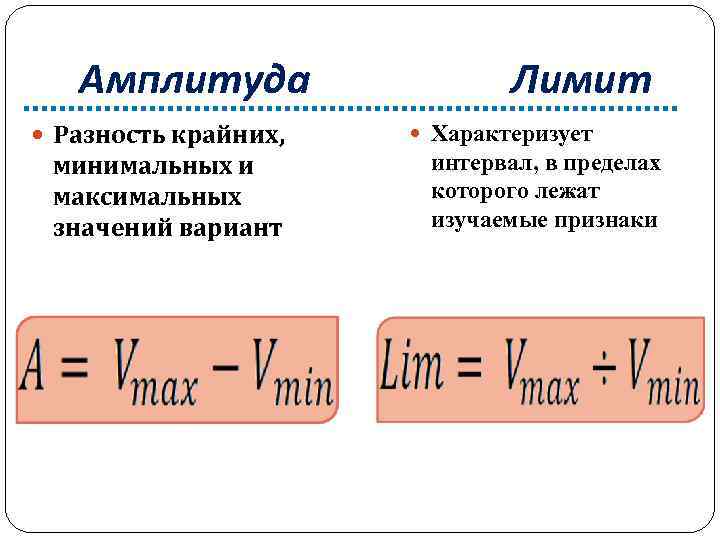Амплитуда Разность крайних, минимальных и максимальных значений вариант Лимит Характеризует интервал, в пределах которого лежат изучаемые признаки

Среднеквадратическое отклонение (σ — cигма) мера колеблемости (вариабельности) вариационного ряда. Сигма — величина именованная, т. е. выражается в тех же единицах, что и варианты ряда

Применение среднеквадратического отклонения для суждения о колеблемости вариационных рядов и сравнительной оценки типичности (представительности) средних арифметических величин. Это необходимо в дифференциальной диагностике при определении устойчивости признаков

Правило «трех сигм» В интервале М± 1σ — 68, 3% вариант ряда В интервале М± 2σ — 95, 5% и В интервале М± 3σ находится 99, 7% всех вариант ряда,

Коэффициент вариации (Cv) процентное отношение среднеквадратического отклонения к среднеарифметической величине это относительная мера колеблемости вариационного ряда

Оценка типичности средней арифметической Если Сv ≤ 10% - степень разнообразия признака малая и такая средняя арифметическая типична для данного вариационного ряда Если Сv ≤ 20% - степень разнообразия признака средняя - средняя арифметическая типична для данного вариационного ряда Если Сv > 20% - степень разнообразия признака сильная и такая средняя арифметическая не достаточно типична для данного вариационного ряда

Средняя величина Обобщающая характеристика размера изучаемого признака. Она позволяет одним числом количественно охарактеризовать качественно однородную совокупность

Применение средних величин для оценки состояния здоровья для оценки организации работы лечебно-профилактических и санитарно-противоэпидемических учреждений, а также деятельности отдельных врачей и других медицинских работников для оценки состояния окружающей среды

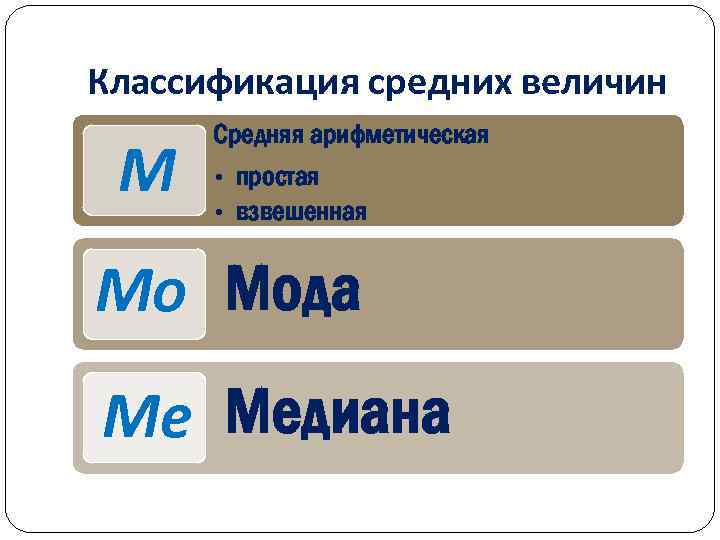Классификация средних величин М Средняя арифметическая • простая • взвешенная Мо Мода Ме Медиана

. Виды проявления количественных связей между признаками

Функциональная связь такой вид соотношения между двумя признаками, когда каждому значению одного из них соответствует строго определенное значение другого Функциональная связь характерна для физикоматематических и химических процессов: - площадь круга зависит от радиуса круга и т. д. - периодическая таблица хим. элементов

Корреляционная связь такая связь, при которой каждому определенному значению одного признака соответствует несколько значений другого взаимосвязанного с ним признака. Корреляционная связь характерна для социально-гигиенических процессов, клинической медицины и биологии. связь между ростом и массой тела человека; связь между температурой тела и частотой пульса и др.

Коэффициент корреляции Величина, характеризующая направление и силу связи между признаками, которая одним числом дает представление о направлении и силе связи между признаками (явлениями).

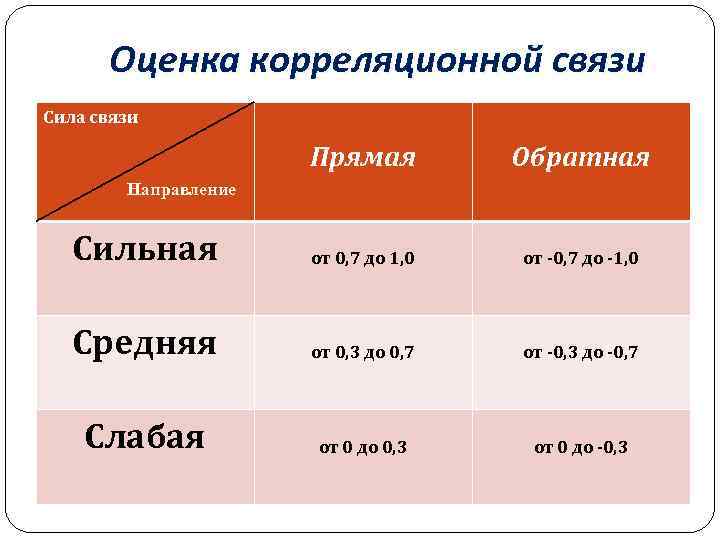Оценка корреляционной связи Сила связи Прямая Обратная Сильная от 0, 7 до 1, 0 от -0, 7 до -1, 0 Средняя от 0, 3 до 0, 7 от -0, 3 до -0, 7 Слабая от 0 до 0, 3 от 0 до -0, 3 Направление