ВАРИАЦИОННЫЕ РЯДЫ И ИХ ХАРАКТЕРИСТИКИ Занятие 5

ВАРИАЦИОННЫЕ РЯДЫ И ИХ ХАРАКТЕРИСТИКИ Занятие 5

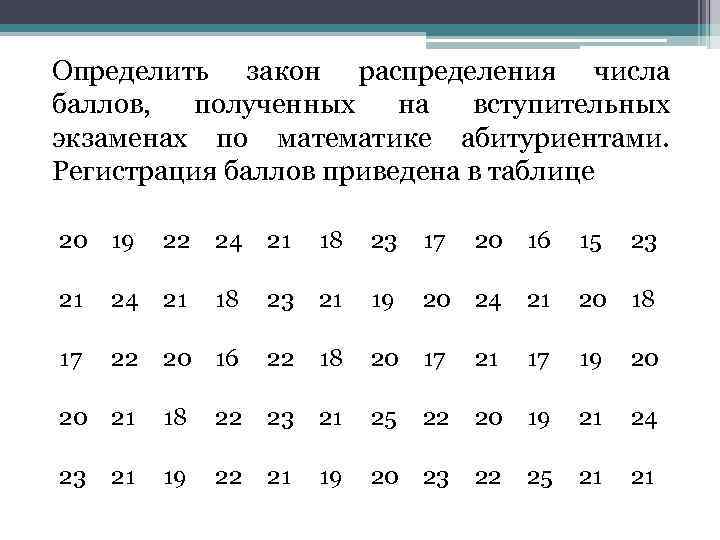Определить закон распределения числа баллов, полученных на вступительных экзаменах по математике абитуриентами. Регистрация баллов приведена в таблице 20 19 22 24 21 18 23 17 21 24 21 18 23 21 19 20 24 17 22 20 16 22 18 20 17 21 20 21 18 22 23 21 25 23 19 22 21 19 20 23 21 22 20 16 15 23 21 20 18 17 19 20 20 19 21 24 22 21 21 25

Определения понятий Объем – число элементов в выборке. Варианта – различные значения признака , наблюдающиеся у членов совокупности. Частота – число, показывающее, сколько раз встречается вариант в совокупности. Частость – отношение частоты варианты к числу членов совокупности , выражают доли (удельные веса) членов совокупности с одинаковыми значениями признака. Частость или частота – вес признака.

Определения понятий Ранжирование ряда – расположить значения вариант в порядке не убывания. Вариационный ряд - ранжированный ряд вариантов с соответствующими им весами. Вариационный ряд называется дискретным, если значения признака отличаются друг от друга не менее, чем на некоторую постоянную величину, и непрерывным, если значения признака могут отличаться на сколь угодно малую величину.

Закон распределения - таблица Дискретный ряд Непрерывный ряд Веса (частоты Значения Веса (частоты или частости) признака или частости) X 1 n 1 От X 1 до X 2 n 1 X 2 n 2 От X 2 до X 3 n 2 …. . . Xm nm От Xm до Xm+1 nm Итого n Варианты

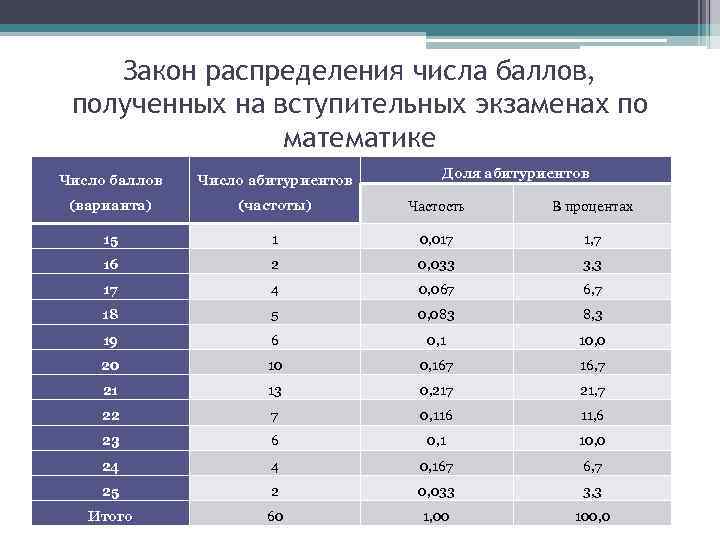Закон распределения числа баллов, полученных на вступительных экзаменах по математике Доля абитуриентов Число баллов Число абитуриентов (варианта) (частоты) Частость В процентах 15 1 0, 017 1, 7 16 2 0, 033 3, 3 17 4 0, 067 6, 7 18 5 0, 083 8, 3 19 6 0, 1 10, 0 20 10 0, 167 16, 7 21 13 0, 217 21, 7 22 7 0, 116 11, 6 23 6 0, 1 10, 0 24 4 0, 167 6, 7 25 2 0, 033 3, 3 Итого 60 1, 00 100, 0

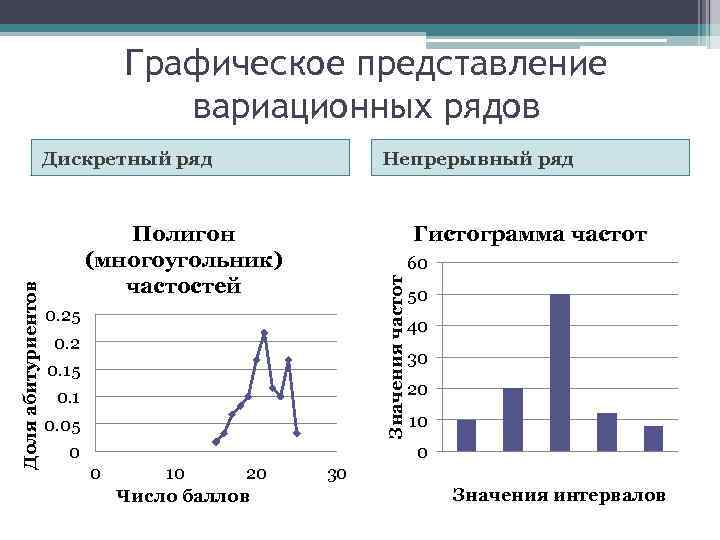Графическое представление вариационных рядов Непрерывный ряд Полигон (многоугольник) частостей Гистограмма частот 60 Значения частот Доля абитуриентов Дискретный ряд 0. 25 0. 2 0. 15 0. 1 0. 05 0 50 40 30 20 10 0 0 10 20 Число баллов 30 Значения интервалов

Построение гистограммы 1. Данные выборки вариационного ряда. представить в виде 2. Определить размах выборки (вариации) 3. Определить объем выборки и количество интервалов по формуле Стерджесса где , - целая часть выражения.

Построение гистограммы 4. Шаг - длина каждого интервала 5. Определить границы каждого интервала

Построение гистограммы 6. Определить частоту каждого интервала, для этого считаем количество элементов выборки попавших в соответствующий интервал. 7. На координатной плоскости строим прямоугольники шириной равной значению интервалов (ось абсцисс) и высотой равной значению частоты или частости (ось ординат).