555ff25bc343383dcb64426c9d52e8dc.ppt
- Количество слайдов: 165
 Valoda Saziņas līdzeklis. Vispārpieņemtā nozīmē – latviešu, krievu, angļu, . . . Zinātņu nozarēs savas valodas. CH 3(CH 2)5 O(CH 2)5 CH 3 “Notācija” vai “pieraksta forma” būtu precīzāks apzīmējums, bet vispārpieņemts ir “valoda”.
Valoda Saziņas līdzeklis. Vispārpieņemtā nozīmē – latviešu, krievu, angļu, . . . Zinātņu nozarēs savas valodas. CH 3(CH 2)5 O(CH 2)5 CH 3 “Notācija” vai “pieraksta forma” būtu precīzāks apzīmējums, bet vispārpieņemts ir “valoda”.
 Programmēšanas valodas Rēķināšanas pieraksts. Jābūt tādai, kas ērta gan APRAKSTĪŠANAI, gan REALIZĀCIJAI. Grūti apvienot, jo • realizācija – zema līmeņa • aprakstīšana – augsta līmeņa Dabiskās valodas, tehniskās valodas un programmēšanas valodas ir līdzīgas.
Programmēšanas valodas Rēķināšanas pieraksts. Jābūt tādai, kas ērta gan APRAKSTĪŠANAI, gan REALIZĀCIJAI. Grūti apvienot, jo • realizācija – zema līmeņa • aprakstīšana – augsta līmeņa Dabiskās valodas, tehniskās valodas un programmēšanas valodas ir līdzīgas.
 Valodu vienības Valodas teikumi sastāv no vārdiem. Vārdi sastāv no simboliem. Divi likumu tipi: 1. Sintakses likumi – nosaka teikumu formu. 2. “Viņi atspiedās pret sienu” 3. “Pret viņi atspiedās sienu” 4. Bināras ciparu virknes 5. 101110101 120
Valodu vienības Valodas teikumi sastāv no vārdiem. Vārdi sastāv no simboliem. Divi likumu tipi: 1. Sintakses likumi – nosaka teikumu formu. 2. “Viņi atspiedās pret sienu” 3. “Pret viņi atspiedās sienu” 4. Bināras ciparu virknes 5. 101110101 120
 Valodu vienības (turp. ) 2. Semantikas likumi – jēga sintaktiski pareizā teikumā 3. Cik daudz ir 101 ? 5, 101 vai kas cits? “No kuģa nokāpa pavisam zaļš jauneklis” Jauns, vai tāds, kuram nelabi? C : = A + B ; A: =1; B: =2; => A: =‘do’; B: =‘re’; => C=3 C=‘dore’
Valodu vienības (turp. ) 2. Semantikas likumi – jēga sintaktiski pareizā teikumā 3. Cik daudz ir 101 ? 5, 101 vai kas cits? “No kuģa nokāpa pavisam zaļš jauneklis” Jauns, vai tāds, kuram nelabi? C : = A + B ; A: =1; B: =2; => A: =‘do’; B: =‘re’; => C=3 C=‘dore’
 Pieraksta formas XX. gs. 60 -tajos gados sakarā ar valodas ALGOL 60 publikāciju programmēšanas valodu sintakses pierakstam lieto Bekusa-Naura formu (BNF). Nav saskatāmas idejas, kā formalizēt semantikas pierakstu. Semantiskās lietas skaidro ar dabisko valodu vārdiem vai piemēriem.
Pieraksta formas XX. gs. 60 -tajos gados sakarā ar valodas ALGOL 60 publikāciju programmēšanas valodu sintakses pierakstam lieto Bekusa-Naura formu (BNF). Nav saskatāmas idejas, kā formalizēt semantikas pierakstu. Semantiskās lietas skaidro ar dabisko valodu vārdiem vai piemēriem.
 Formālā valodu teorija (Definīcijas) Simbols ir atomāra vienība, ko apzīmē ar simbolu vai rezervētu atslēgas vārdu. Būtiski, ka simbols tālāk nedalās. + , ; BEGIN END Programmēšanā piecas kategorijas – konstantes, identifikatori, operatori, rezervēti vārdi, atdalītāji.
Formālā valodu teorija (Definīcijas) Simbols ir atomāra vienība, ko apzīmē ar simbolu vai rezervētu atslēgas vārdu. Būtiski, ka simbols tālāk nedalās. + , ; BEGIN END Programmēšanā piecas kategorijas – konstantes, identifikatori, operatori, rezervēti vārdi, atdalītāji.
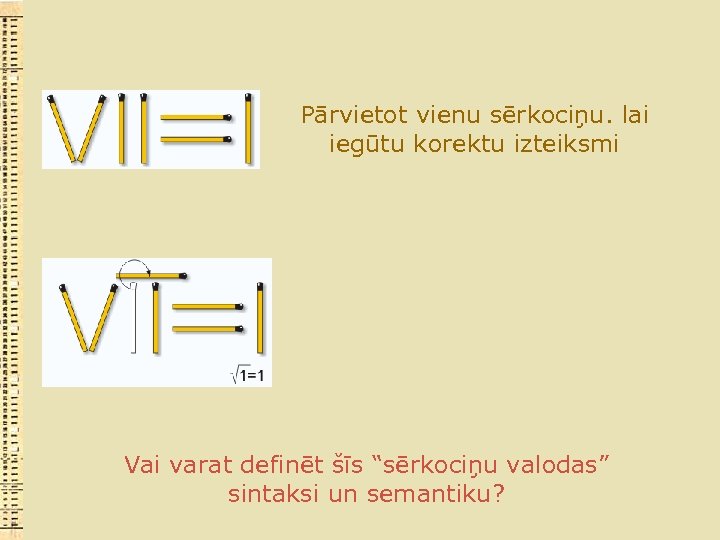 Pārvietot vienu sērkociņu. lai iegūtu korektu izteiksmi Vai varat definēt šīs “sērkociņu valodas” sintaksi un semantiku?
Pārvietot vienu sērkociņu. lai iegūtu korektu izteiksmi Vai varat definēt šīs “sērkociņu valodas” sintaksi un semantiku?
 Definīcijas (turp. ) Alfabēts (simbolu klase) ir netukša galīga simbolu kopa. Piemēri: burti, burti un cipari, {0, 1} + - / * a b c : = ( ) { switch } Lietosim pēc apjoma mazus alfabētus. Vai ir pazīstams kāds liela apjoma alfabēts?
Definīcijas (turp. ) Alfabēts (simbolu klase) ir netukša galīga simbolu kopa. Piemēri: burti, burti un cipari, {0, 1} + - / * a b c : = ( ) { switch } Lietosim pēc apjoma mazus alfabētus. Vai ir pazīstams kāds liela apjoma alfabēts?
 Definīcijas (turp. ) No alfabēta simboliem var veidot galīgas simbolu virknes =a 1 a 2. . . an, kur a 1 , a 2 , . . . , an ir simboli no . Virknes garums | | ir tajā ietilpstošo simbolu skaits. |abrakadabra| = 11
Definīcijas (turp. ) No alfabēta simboliem var veidot galīgas simbolu virknes =a 1 a 2. . . an, kur a 1 , a 2 , . . . , an ir simboli no . Virknes garums | | ir tajā ietilpstošo simbolu skaits. |abrakadabra| = 11
 Virkņu operācijas • Konkatenēšana w = a 1 a 2. . . an v = b 1 b 2. . . bk wv = a 1 a 2. . . anb 1 b 2. . . bk Konkatenētās virknes garums: |wv| = |w|+|v|
Virkņu operācijas • Konkatenēšana w = a 1 a 2. . . an v = b 1 b 2. . . bk wv = a 1 a 2. . . anb 1 b 2. . . bk Konkatenētās virknes garums: |wv| = |w|+|v|
 Virkņu operācijas • Apgriešana w = a 1 a 2. . . an w. R = an. . . a 2 a 1
Virkņu operācijas • Apgriešana w = a 1 a 2. . . an w. R = an. . . a 2 a 1
 Definīcijas (turp. ) Bieži ir izdevīgi pieļaut tukšās virknes esamību, ko apzīmē ar (citi ar ). Īpašība – konkatenējot ar citu virkni šī virkne netiek mainīta a = a
Definīcijas (turp. ) Bieži ir izdevīgi pieļaut tukšās virknes esamību, ko apzīmē ar (citi ar ). Īpašība – konkatenējot ar citu virkni šī virkne netiek mainīta a = a
 Virkņu operācijas • Atkārtošana wk = wwwww. . . w k reizes w 0 = Piemērs: (abba)3 = abbaabba
Virkņu operācijas • Atkārtošana wk = wwwww. . . w k reizes w 0 = Piemērs: (abba)3 = abbaabba
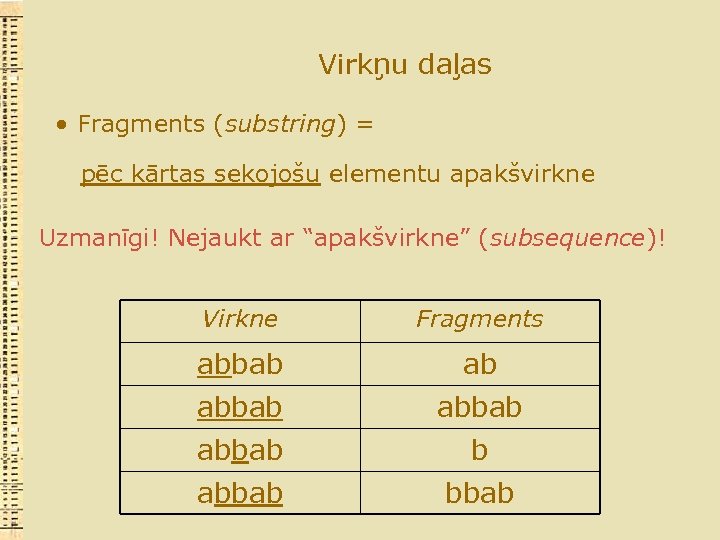 Virkņu daļas • Fragments (substring) = pēc kārtas sekojošu elementu apakšvirkne Uzmanīgi! Nejaukt ar “apakšvirkne” (subsequence)! Virkne Fragments abbab abbab
Virkņu daļas • Fragments (substring) = pēc kārtas sekojošu elementu apakšvirkne Uzmanīgi! Nejaukt ar “apakšvirkne” (subsequence)! Virkne Fragments abbab abbab
 Virkņu daļas • Prefikss – virknes sākuma fragments u (var būt garumā 0) • Sufikss – virknes beigu fragments v (var būt garumā 0) w = uv
Virkņu daļas • Prefikss – virknes sākuma fragments u (var būt garumā 0) • Sufikss – virknes beigu fragments v (var būt garumā 0) w = uv
 Piemērs abbab Prefikss Sufikss abbab ab bab ab abbab
Piemērs abbab Prefikss Sufikss abbab ab bab ab abbab
 Definīcijas (turp. ) Visu virkņu, kas veidotas no un ir garumā n, kopu apzīmē ar n. Visu virkņu (ieskaitot tukšo virkni) kopa tiek saukta par Klīnija slēgumu (Kleene closure) un tiek apzīmēta ar *. Visu alfabēta virkņu, kuru garums ir vismaz 1, kopa tiek saukta par pozitīvo slēgumu un apzīmēta ar +. Tātad, + 1 2 3 . . . * 0 +
Definīcijas (turp. ) Visu virkņu, kas veidotas no un ir garumā n, kopu apzīmē ar n. Visu virkņu (ieskaitot tukšo virkni) kopa tiek saukta par Klīnija slēgumu (Kleene closure) un tiek apzīmēta ar *. Visu alfabēta virkņu, kuru garums ir vismaz 1, kopa tiek saukta par pozitīvo slēgumu un apzīmēta ar +. Tātad, + 1 2 3 . . . * 0 +
 Definīcijas (turp. ) Valoda V, kas veidota no alfabēta , ir * apakškopa. V * Alfabēta virknes, kas pieder valodai V, tiek sauktas par valodas V vārdiem. Valodas apjoms ir valodā ietilpstošo vārdu skaits. V = {a, b, abba} |V| = 4
Definīcijas (turp. ) Valoda V, kas veidota no alfabēta , ir * apakškopa. V * Alfabēta virknes, kas pieder valodai V, tiek sauktas par valodas V vārdiem. Valodas apjoms ir valodā ietilpstošo vārdu skaits. V = {a, b, abba} |V| = 4
 Piemērs = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} V ir visu to piecciparu skaitļu, kuru cipari ir dilstošā secībā, kopa. Piemēram, 98721 V, 76013 V. |V| = ? 252
Piemērs = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} V ir visu to piecciparu skaitļu, kuru cipari ir dilstošā secībā, kopa. Piemēram, 98721 V, 76013 V. |V| = ? 252
 Valodas uzdošanas veidi Ja valodas vārdu daudzums ir galīgs, tos var pārskaitīt. Ja vārdu daudzums ir bezgalīgs, nepieciešams definēt kādu likumu, kā šos vārdus veidot.
Valodas uzdošanas veidi Ja valodas vārdu daudzums ir galīgs, tos var pārskaitīt. Ja vārdu daudzums ir bezgalīgs, nepieciešams definēt kādu likumu, kā šos vārdus veidot.
![Piemērs = {a, b, +, [, ]} L={ ([a+)n (b])n | n>0 } n=1: Piemērs = {a, b, +, [, ]} L={ ([a+)n (b])n | n>0 } n=1:](https://present5.com/presentation/555ff25bc343383dcb64426c9d52e8dc/image-21.jpg) Piemērs = {a, b, +, [, ]} L={ ([a+)n (b])n | n>0 } n=1: [a+b] n=2: [a+[a+b]b] n=3: [a+[a+[a+b]b]b] . . . tādas, ka
Piemērs = {a, b, +, [, ]} L={ ([a+)n (b])n | n>0 } n=1: [a+b] n=2: [a+[a+b]b] n=3: [a+[a+[a+b]b]b] . . . tādas, ka
 Piemērs Latviešu valoda = { A, Ā, B, C, Č, D, E, Ē, F, G, Ģ, H, I, Ī, J, K, Ķ, L, Ļ, M, N, Ņ, O, P, R, S, Š, T, U, Ū, V, Z, Ž, a, ā, b, c, č, d, e, ē, f, g, ģ, h, i, ī, j, k, ķ, l, ļ, m, n, ņ, o, p, r, s, š, t, u, ū, v, z, ž} Vārdi ir “kaķis”, ”suns”, ”māja”. Virknes ir arī “ķčšž”, “počemučka”, “freimvorks” Nav virknes: “jox”, “ne 1”, “po 4 emu 4 ka”, “web” Kā ar visu vārdu uzdošanu? Kāds ir latviešu valodas apjoms?
Piemērs Latviešu valoda = { A, Ā, B, C, Č, D, E, Ē, F, G, Ģ, H, I, Ī, J, K, Ķ, L, Ļ, M, N, Ņ, O, P, R, S, Š, T, U, Ū, V, Z, Ž, a, ā, b, c, č, d, e, ē, f, g, ģ, h, i, ī, j, k, ķ, l, ļ, m, n, ņ, o, p, r, s, š, t, u, ū, v, z, ž} Vārdi ir “kaķis”, ”suns”, ”māja”. Virknes ir arī “ķčšž”, “počemučka”, “freimvorks” Nav virknes: “jox”, “ne 1”, “po 4 emu 4 ka”, “web” Kā ar visu vārdu uzdošanu? Kāds ir latviešu valodas apjoms?
 Operācijas ar valodām Apvienošana V 1 V 2={s|s V 1 v s V 2} Šķēlums V 1 V 2={s|s V 1 & v s V 2} Konkatenēšana V 1 V 2={st|s V 1 & t V 2} Starpība V 1 -V 2={s|s V 1 & s V 2} Papildinājums V= * - V Apgriešana VR= {w. R|w V} Atkārtošana Vn= {w 1 w 2. . . wn|w 1, w 2, . . . , wn V} Zvaigznes slēgums V*= V 0 V 1 V 2 . . . Pozitīvais slēgums V+= V*-{ }
Operācijas ar valodām Apvienošana V 1 V 2={s|s V 1 v s V 2} Šķēlums V 1 V 2={s|s V 1 & v s V 2} Konkatenēšana V 1 V 2={st|s V 1 & t V 2} Starpība V 1 -V 2={s|s V 1 & s V 2} Papildinājums V= * - V Apgriešana VR= {w. R|w V} Atkārtošana Vn= {w 1 w 2. . . wn|w 1, w 2, . . . , wn V} Zvaigznes slēgums V*= V 0 V 1 V 2 . . . Pozitīvais slēgums V+= V*-{ }
 Piemērs = {a, b} V 1 V 2 = ? V 1 V 2 = ? V 1 -V 2 = ? V 2 -V 1 = ? V 1 R = ? V 22 = ? V 1={a, ab, aaaa} V 2={bb, ab}
Piemērs = {a, b} V 1 V 2 = ? V 1 V 2 = ? V 1 -V 2 = ? V 2 -V 1 = ? V 1 R = ? V 22 = ? V 1={a, ab, aaaa} V 2={bb, ab}
 Piemērs = {a, b} V 1={a, ab, aaaa} V 1 V 2 = {a, ab, aaaa, bb} V 1 V 2 = ? V 1 -V 2 = ? V 2 -V 1 = ? V 1 R = ? V 22 = ? V 2={bb, ab}
Piemērs = {a, b} V 1={a, ab, aaaa} V 1 V 2 = {a, ab, aaaa, bb} V 1 V 2 = ? V 1 -V 2 = ? V 2 -V 1 = ? V 1 R = ? V 22 = ? V 2={bb, ab}
 Piemērs = {a, b} V 1={a, ab, aaaa} V 1 V 2 = {a, ab, aaaa, bb} V 1 V 2 = {ab} V 1 V 2 = ? V 1 -V 2 = ? V 2 -V 1 = ? V 1 R = ? V 22 = ? V 2={bb, ab}
Piemērs = {a, b} V 1={a, ab, aaaa} V 1 V 2 = {a, ab, aaaa, bb} V 1 V 2 = {ab} V 1 V 2 = ? V 1 -V 2 = ? V 2 -V 1 = ? V 1 R = ? V 22 = ? V 2={bb, ab}
 Piemērs = {a, b} V 1={a, ab, aaaa} V 2={bb, ab} V 1 V 2 = {a, ab, aaaa, bb} V 1 V 2 = {ab} V 1 V 2 = {abb, aab, abbb, abab, aaaabb, aaaaab} V 1 -V 2 = ? V 2 -V 1 = ? V 1 R = ? V 22 = ?
Piemērs = {a, b} V 1={a, ab, aaaa} V 2={bb, ab} V 1 V 2 = {a, ab, aaaa, bb} V 1 V 2 = {ab} V 1 V 2 = {abb, aab, abbb, abab, aaaabb, aaaaab} V 1 -V 2 = ? V 2 -V 1 = ? V 1 R = ? V 22 = ?
 Piemērs = {a, b} V 1={a, ab, aaaa} V 2={bb, ab} V 1 V 2 = {a, ab, aaaa, bb} V 1 V 2 = {ab} V 1 V 2 = {abb, aab, abbb, abab, aaaabb, aaaaab} V 1 -V 2 = {a, aaaa} V 2 -V 1 = ? V 1 R = ? V 22 = ?
Piemērs = {a, b} V 1={a, ab, aaaa} V 2={bb, ab} V 1 V 2 = {a, ab, aaaa, bb} V 1 V 2 = {ab} V 1 V 2 = {abb, aab, abbb, abab, aaaabb, aaaaab} V 1 -V 2 = {a, aaaa} V 2 -V 1 = ? V 1 R = ? V 22 = ?
 Piemērs = {a, b} V 1={a, ab, aaaa} V 2={bb, ab} V 1 V 2 = {a, ab, aaaa, bb} V 1 V 2 = {ab} V 1 V 2 = {abb, aab, abbb, abab, aaaabb, aaaaab} V 1 -V 2 = {a, aaaa} V 2 -V 1 = {bb} V 1 R = ? V 22 = ?
Piemērs = {a, b} V 1={a, ab, aaaa} V 2={bb, ab} V 1 V 2 = {a, ab, aaaa, bb} V 1 V 2 = {ab} V 1 V 2 = {abb, aab, abbb, abab, aaaabb, aaaaab} V 1 -V 2 = {a, aaaa} V 2 -V 1 = {bb} V 1 R = ? V 22 = ?
 Piemērs = {a, b} V 1={a, ab, aaaa} V 2={bb, ab} V 1 V 2 = {a, ab, aaaa, bb} V 1 V 2 = {ab} V 1 V 2 = {abb, aab, abbb, abab, aaaabb, aaaaab} V 1 -V 2 = {a, aaaa} V 2 -V 1 = {bb} V 1 R = {a, ba, aaaa} V 22 = ?
Piemērs = {a, b} V 1={a, ab, aaaa} V 2={bb, ab} V 1 V 2 = {a, ab, aaaa, bb} V 1 V 2 = {ab} V 1 V 2 = {abb, aab, abbb, abab, aaaabb, aaaaab} V 1 -V 2 = {a, aaaa} V 2 -V 1 = {bb} V 1 R = {a, ba, aaaa} V 22 = ?
 Piemērs = {a, b} V 1={a, ab, aaaa} V 2={bb, ab} V 1 V 2 = {a, ab, aaaa, bb} V 1 V 2 = {ab} V 1 V 2 = {abb, aab, abbb, abab, aaaabb, aaaaab} V 1 -V 2 = {a, aaaa} V 2 -V 1 = {bb} V 1 R = {a, ba, aaaa} V 22 = {bbbb, bbab, abbb, abab}
Piemērs = {a, b} V 1={a, ab, aaaa} V 2={bb, ab} V 1 V 2 = {a, ab, aaaa, bb} V 1 V 2 = {ab} V 1 V 2 = {abb, aab, abbb, abab, aaaabb, aaaaab} V 1 -V 2 = {a, aaaa} V 2 -V 1 = {bb} V 1 R = {a, ba, aaaa} V 22 = {bbbb, bbab, abbb, abab}
 Vai taisnība, ka … (V 1 V 2)R = V 1 R V 2 R (V 1 V 2)R = V 2 R V 1 R (V 1 V 2) = (V 1 V 1 V 1 V 2) (V 2 V 1 V 2 V 2) Pretpiemērs: V 1={a, ab, b} V 2={ab, ba}
Vai taisnība, ka … (V 1 V 2)R = V 1 R V 2 R (V 1 V 2)R = V 2 R V 1 R (V 1 V 2) = (V 1 V 1 V 1 V 2) (V 2 V 1 V 2 V 2) Pretpiemērs: V 1={a, ab, b} V 2={ab, ba}
 Piemēri (“Kas tas ir vienkāršos vārdos? ”) Ja B={A, B, …, Z, a, b, …, z}, C={0, 1, 2, …, 9}, tad • B C • B 4 • B* • B(B C)* • C+
Piemēri (“Kas tas ir vienkāršos vārdos? ”) Ja B={A, B, …, Z, a, b, …, z}, C={0, 1, 2, …, 9}, tad • B C • B 4 • B* • B(B C)* • C+
 Piemēri Ja B={A, B, …, Z, a, b, …, z}, C={0, 1, 2, …, 9}, tad • B C - burtu un ciparu kopa • BC • B 4 • B* • B(B C)* • C+
Piemēri Ja B={A, B, …, Z, a, b, …, z}, C={0, 1, 2, …, 9}, tad • B C - burtu un ciparu kopa • BC • B 4 • B* • B(B C)* • C+
 Piemēri Ja B={A, B, …, Z, a, b, …, z}, C={0, 1, 2, …, 9}, tad • B C - burtu un ciparu kopa • BC – to virkņu, kas sastāv no burta un cipara, kopa • B 4 • B* • B(B C)* • C+
Piemēri Ja B={A, B, …, Z, a, b, …, z}, C={0, 1, 2, …, 9}, tad • B C - burtu un ciparu kopa • BC – to virkņu, kas sastāv no burta un cipara, kopa • B 4 • B* • B(B C)* • C+
 Piemēri Ja B={A, B, …, Z, a, b, …, z}, C={0, 1, 2, …, 9}, tad • B C - burtu un ciparu kopa • BC – to virkņu, kas sastāv no burta un cipara, kopa • B 4 – visu četrburtīgo vārdu kopa • B* • B(B C)* • C+
Piemēri Ja B={A, B, …, Z, a, b, …, z}, C={0, 1, 2, …, 9}, tad • B C - burtu un ciparu kopa • BC – to virkņu, kas sastāv no burta un cipara, kopa • B 4 – visu četrburtīgo vārdu kopa • B* • B(B C)* • C+
 Piemēri Ja B={A, B, …, Z, a, b, …, z}, C={0, 1, 2, …, 9}, tad • B C - burtu un ciparu kopa • BC – to virkņu, kas sastāv no burta un cipara, kopa • B 4 – visu četrburtīgo vārdu kopa • B*- visu burtu virkņu un tukšās virknes kopa • B(B C)* • C+
Piemēri Ja B={A, B, …, Z, a, b, …, z}, C={0, 1, 2, …, 9}, tad • B C - burtu un ciparu kopa • BC – to virkņu, kas sastāv no burta un cipara, kopa • B 4 – visu četrburtīgo vārdu kopa • B*- visu burtu virkņu un tukšās virknes kopa • B(B C)* • C+
 Piemēri Ja B={A, B, …, Z, a, b, …, z}, C={0, 1, 2, …, 9}, tad • B C - burtu un ciparu kopa • BC – to virkņu, kas sastāv no burta un cipara, kopa • B 4 – visu četrburtīgo vārdu kopa • B*- visu burtu virkņu un tukšās virknes kopa • B(B C)* - burtu un ciparu virknes, kas sākas ar burtu • C+
Piemēri Ja B={A, B, …, Z, a, b, …, z}, C={0, 1, 2, …, 9}, tad • B C - burtu un ciparu kopa • BC – to virkņu, kas sastāv no burta un cipara, kopa • B 4 – visu četrburtīgo vārdu kopa • B*- visu burtu virkņu un tukšās virknes kopa • B(B C)* - burtu un ciparu virknes, kas sākas ar burtu • C+
 Piemēri Ja B={A, B, …, Z, a, b, …, z}, C={0, 1, 2, …, 9}, tad • B C - burtu un ciparu kopa • BC – to virkņu, kas sastāv no burta un cipara, kopa • B 4 – visu četrburtīgo vārdu kopa • B*- visu burtu virkņu un tukšās virknes kopa • B(B C)* - burtu un ciparu virknes, kas sākas ar burtu • C+ - ciparu virknes, kas sastāv no viena vairāk cipariem
Piemēri Ja B={A, B, …, Z, a, b, …, z}, C={0, 1, 2, …, 9}, tad • B C - burtu un ciparu kopa • BC – to virkņu, kas sastāv no burta un cipara, kopa • B 4 – visu četrburtīgo vārdu kopa • B*- visu burtu virkņu un tukšās virknes kopa • B(B C)* - burtu un ciparu virknes, kas sākas ar burtu • C+ - ciparu virknes, kas sastāv no viena vairāk cipariem
 Piemēri Ja B={A, B, …, Z, a, b, …, z}, C={0, 1, 2, …, 9}, tad • Kā pierakstīt visus naturālos skaitļus (pieraksts nesākas ar 0)? (C-{0})C*
Piemēri Ja B={A, B, …, Z, a, b, …, z}, C={0, 1, 2, …, 9}, tad • Kā pierakstīt visus naturālos skaitļus (pieraksts nesākas ar 0)? (C-{0})C*
 Regulāras izteiksmes Dažu vienkāršu valodu vārdus var specificēt, izmantojot regulāras izteiksmes. Nosaka likumu, kā alfabēta simboli var tikt sasaistīti, lai veidotu vārdu. Aprakstīšanai izmanto metasimbolus. Valodu, ko nosaka regulāra izteiksme r, apzīmē L(r)
Regulāras izteiksmes Dažu vienkāršu valodu vārdus var specificēt, izmantojot regulāras izteiksmes. Nosaka likumu, kā alfabēta simboli var tikt sasaistīti, lai veidotu vārdu. Aprakstīšanai izmanto metasimbolus. Valodu, ko nosaka regulāra izteiksme r, apzīmē L(r)
 Metasimboli a) konkatenācija – simboli vai simbolu virknes, kas uzrakstīti viens otram galā, var tikt “salipināti kopā”. Tā arī raksta: XY. Dažreiz pieraksta kā X. Y. b) alternatīva – izvēle starp diviem simboliem vai simbolu virknēm. Apzīmē ar vertikālu svītru. X|Y c) atkārtošana – simbols vai simbolu virkne X aiz kura ir metasimbols * nozīmē, ka X var atkārtot 0 vairāk reižu. d) grupēšana – simbolu grupu var iekļaut iekavās ( un ). e) Pastāv vienošanās par prioritātēm – f) grupēšana>atkārtošana>konkatenācija>alternatīv a
Metasimboli a) konkatenācija – simboli vai simbolu virknes, kas uzrakstīti viens otram galā, var tikt “salipināti kopā”. Tā arī raksta: XY. Dažreiz pieraksta kā X. Y. b) alternatīva – izvēle starp diviem simboliem vai simbolu virknēm. Apzīmē ar vertikālu svītru. X|Y c) atkārtošana – simbols vai simbolu virkne X aiz kura ir metasimbols * nozīmē, ka X var atkārtot 0 vairāk reižu. d) grupēšana – simbolu grupu var iekļaut iekavās ( un ). e) Pastāv vienošanās par prioritātēm – f) grupēšana>atkārtošana>konkatenācija>alternatīv a
 Regulāras izteiksmes (formāla definīcija) 1. Regulāra izteiksme r definē valodu L(r). 2. ir regulāra izteiksme, kas apzīmē tukšu vārdu (virkņu) kopu. 3. ir regulāra izteiksme, kas apzīmē { } – t. i. kopu, kas sastāv tikai no tukšā vārda. 4. Ja ir simbols no alfabēta , tad ir regulāra izteiksme, kas apzīmē kopu { } – t. i. kopu, kas satur tikai vārdu . Uzmanīgi ar apzīmējumiem – šeit piedalās simbols, vārds, regulāra izteiksme!
Regulāras izteiksmes (formāla definīcija) 1. Regulāra izteiksme r definē valodu L(r). 2. ir regulāra izteiksme, kas apzīmē tukšu vārdu (virkņu) kopu. 3. ir regulāra izteiksme, kas apzīmē { } – t. i. kopu, kas sastāv tikai no tukšā vārda. 4. Ja ir simbols no alfabēta , tad ir regulāra izteiksme, kas apzīmē kopu { } – t. i. kopu, kas satur tikai vārdu . Uzmanīgi ar apzīmējumiem – šeit piedalās simbols, vārds, regulāra izteiksme!
 Regulāras izteiksmes (formāla definīcija turp. ) 5. Ja A ir regulāra izteiksme, tad (A) arī ir regulāra izteiksme, kas apraksta valodu L(A). 6. Ja A ir regulāra izteiksme, tad A* arī ir regulāra izteiksme, kas apraksta valodu L(A)*. 7. Ja A un B ir regulāras izteiksmes, tad AB arī ir regulāra izteiksme, kas apraksta valodu L(A)L(B). 8. Ja A un B ir regulāras izteiksmes, tad A|B arī ir regulāra izteiksme, kas apraksta valodu L(A) L(B).
Regulāras izteiksmes (formāla definīcija turp. ) 5. Ja A ir regulāra izteiksme, tad (A) arī ir regulāra izteiksme, kas apraksta valodu L(A). 6. Ja A ir regulāra izteiksme, tad A* arī ir regulāra izteiksme, kas apraksta valodu L(A)*. 7. Ja A un B ir regulāras izteiksmes, tad AB arī ir regulāra izteiksme, kas apraksta valodu L(A)L(B). 8. Ja A un B ir regulāras izteiksmes, tad A|B arī ir regulāra izteiksme, kas apraksta valodu L(A) L(B).
 Īpašības 1)Pastāv vienošanās par prioritātēm – grupēšana>atkārtošana>konkatenācija>alternatīva 2)Ja pats metasimbols ir iekļauts alfabētā, tas jāiekļauj pēdiņās. Piemēram, PASCAL komentārs 3) “(“ “*” c* “*” “)” , kur c A
Īpašības 1)Pastāv vienošanās par prioritātēm – grupēšana>atkārtošana>konkatenācija>alternatīva 2)Ja pats metasimbols ir iekļauts alfabētā, tas jāiekļauj pēdiņās. Piemēram, PASCAL komentārs 3) “(“ “*” c* “*” “)” , kur c A
 Citi metasimboli Iespējami arī citi metasimboli un saīsinājumi: A+ - A atkārtošana vismaz vienu reizi A? - neobligāts A [a-gi-z. ABF] - divi mazo burtu diapazoni un trīs lielie burti Vai minētos metasimbolus var modelēt ar “klasiskajiem”? a+ a? [a-e. BC]
Citi metasimboli Iespējami arī citi metasimboli un saīsinājumi: A+ - A atkārtošana vismaz vienu reizi A? - neobligāts A [a-gi-z. ABF] - divi mazo burtu diapazoni un trīs lielie burti Vai minētos metasimbolus var modelēt ar “klasiskajiem”? a+ a? [a-e. BC]
![Citi metasimboli (turp. ) a+ aa* a? a| [a-e. BC] = a|b|c|d|e|B|C Citi metasimboli (turp. ) a+ aa* a? a| [a-e. BC] = a|b|c|d|e|B|C](https://present5.com/presentation/555ff25bc343383dcb64426c9d52e8dc/image-47.jpg) Citi metasimboli (turp. ) a+ aa* a? a| [a-e. BC] = a|b|c|d|e|B|C
Citi metasimboli (turp. ) a+ aa* a? a| [a-e. BC] = a|b|c|d|e|B|C
 Vienas valodas dažādas notācijas L( 1(1|01)*0 )= L( 10 ) L( 1(1|01)(1|01)0 ) . . . = { 10, 1010, 11010, 101010, . . . } L( 11*(011*)*0 )
Vienas valodas dažādas notācijas L( 1(1|01)*0 )= L( 10 ) L( 1(1|01)(1|01)0 ) . . . = { 10, 1010, 11010, 101010, . . . } L( 11*(011*)*0 )
 Piemērs • Kā pierakstīt visas tādas binārās virknes, kurās nekādi divi vieninieki neatrodas blakus? L( 0*( (100*)* | 1(00*1)*) 0* )
Piemērs • Kā pierakstīt visas tādas binārās virknes, kurās nekādi divi vieninieki neatrodas blakus? L( 0*( (100*)* | 1(00*1)*) 0* )
 Algebriskās īpašības A|B = B|A (alternatīvu komutativitāte) A|(B|C) = (A|B)|C (alternatīvu asociativitāte) A|A = A (alternatīvu absorbcija) A. (B. C)= (A. B). C (konkatenācijas asociativitāte) A. (B|C) = A. B|A. C (kreisā distributivitāte) (A|B). C = A. C|B. C (labā distributivitāte) A = A (konkatenācijas identitāte) A*A* = A* (slēguma absorbcija)
Algebriskās īpašības A|B = B|A (alternatīvu komutativitāte) A|(B|C) = (A|B)|C (alternatīvu asociativitāte) A|A = A (alternatīvu absorbcija) A. (B. C)= (A. B). C (konkatenācijas asociativitāte) A. (B|C) = A. B|A. C (kreisā distributivitāte) (A|B). C = A. C|B. C (labā distributivitāte) A = A (konkatenācijas identitāte) A*A* = A* (slēguma absorbcija)
 Piemēri Regulāras izteiksmes ir interesantas, jo var aprakstīt programmēšanas valodas vārdus (identifikatorus, simbolu virkņu konstantes, komentārus). Veselie skaitļi ir aprakstāmi kā 0|(-| ). (1|2|3|4|5|6|7|8|9). (0|1|2|3|4|5|6|7|8|9)*
Piemēri Regulāras izteiksmes ir interesantas, jo var aprakstīt programmēšanas valodas vārdus (identifikatorus, simbolu virkņu konstantes, komentārus). Veselie skaitļi ir aprakstāmi kā 0|(-| ). (1|2|3|4|5|6|7|8|9). (0|1|2|3|4|5|6|7|8|9)*
 Regulāras definīcijas Regulāras izteiksmēm var piešķirt savus nosaukumus un izmantot jau šos nosaukumus kā simbolus. Ja Σ ir bāzes simbolu alfabēts, tad regulāra definīcija sastāv no definīciju virknes d 1: : =r 1, d 2: : =r 2, …, dn: : = rn, kur di – individuālais izteiksmes vārds, ri – regulāra izteiksme, kas sastāv no Σ (d 1, d 2, …, di-1) simboliem. Ja ri izmanto dj, kur j≥i, tad ri var būt definēts rekursīvi un aizvietošana var nebeigties. Veselie skaitļi ir aprakstāmi kā
Regulāras definīcijas Regulāras izteiksmēm var piešķirt savus nosaukumus un izmantot jau šos nosaukumus kā simbolus. Ja Σ ir bāzes simbolu alfabēts, tad regulāra definīcija sastāv no definīciju virknes d 1: : =r 1, d 2: : =r 2, …, dn: : = rn, kur di – individuālais izteiksmes vārds, ri – regulāra izteiksme, kas sastāv no Σ (d 1, d 2, …, di-1) simboliem. Ja ri izmanto dj, kur j≥i, tad ri var būt definēts rekursīvi un aizvietošana var nebeigties. Veselie skaitļi ir aprakstāmi kā
 Ja valodu var aprakstīt ar regulāru izteiksmi, tad šo valodu sauc par regulāru. r – regulāra izteiksme L(r) – regulāra valoda Kādas valodas nav regulāras? Piemēram, sabalansētu iekavu virkņu valoda: {ε, ()(), (()), ()()(), (())(), ()(()), ((())), …}
Ja valodu var aprakstīt ar regulāru izteiksmi, tad šo valodu sauc par regulāru. r – regulāra izteiksme L(r) – regulāra valoda Kādas valodas nav regulāras? Piemēram, sabalansētu iekavu virkņu valoda: {ε, ()(), (()), ()()(), (())(), ()(()), ((())), …}
 Citi regulāru valodu uzdošanas veidi Galīgi nedeterminēti akceptētāji (GNA)
Citi regulāru valodu uzdošanas veidi Galīgi nedeterminēti akceptētāji (GNA)
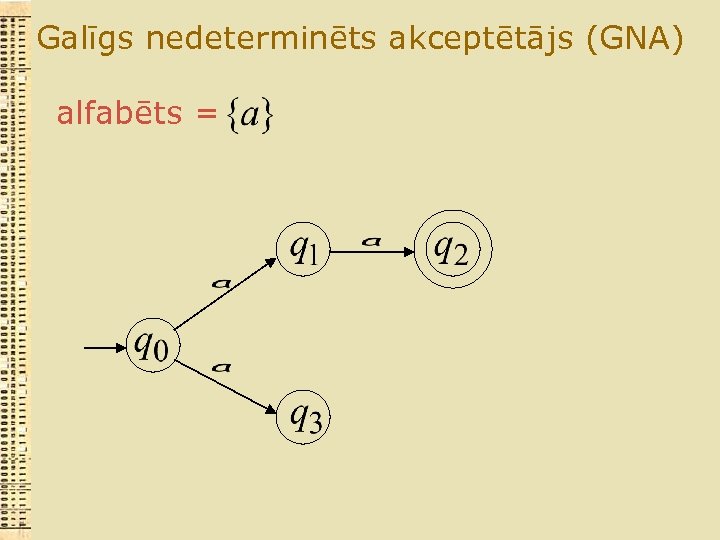 Galīgs nedeterminēts akceptētājs (GNA) alfabēts =
Galīgs nedeterminēts akceptētājs (GNA) alfabēts =
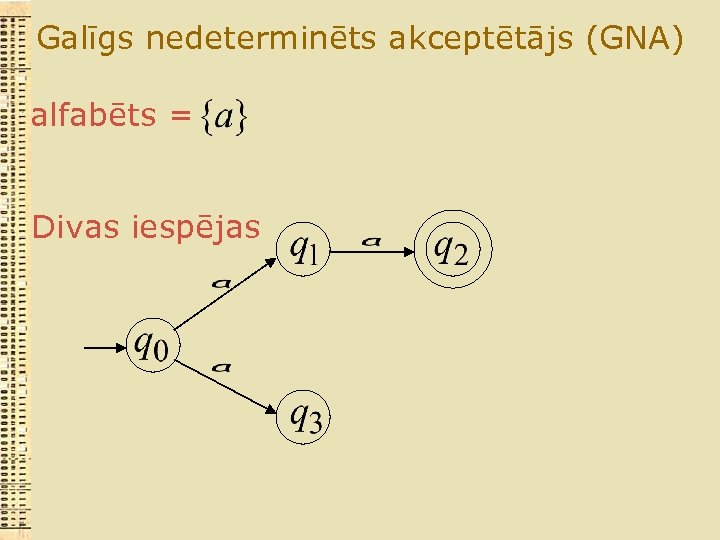 Galīgs nedeterminēts akceptētājs (GNA) alfabēts = Divas iespējas
Galīgs nedeterminēts akceptētājs (GNA) alfabēts = Divas iespējas
 Galīgs nedeterminēts akceptētājs (GNA) alfabēts = Divas iespējas Nav pārejas
Galīgs nedeterminēts akceptētājs (GNA) alfabēts = Divas iespējas Nav pārejas
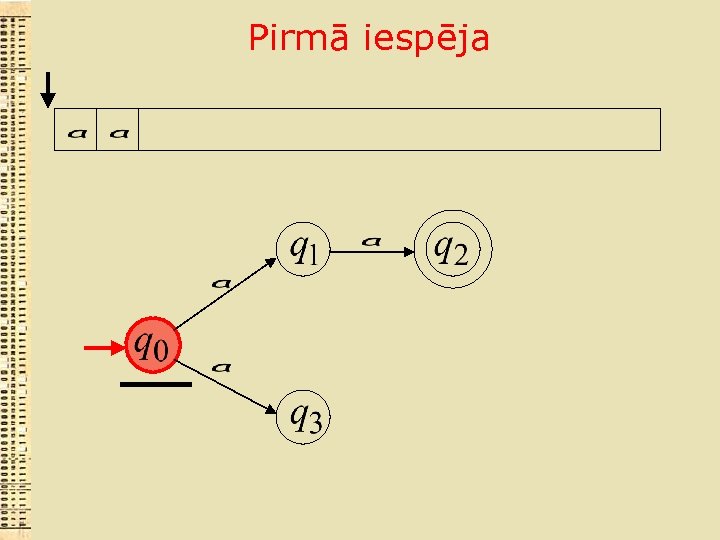 Pirmā iespēja
Pirmā iespēja
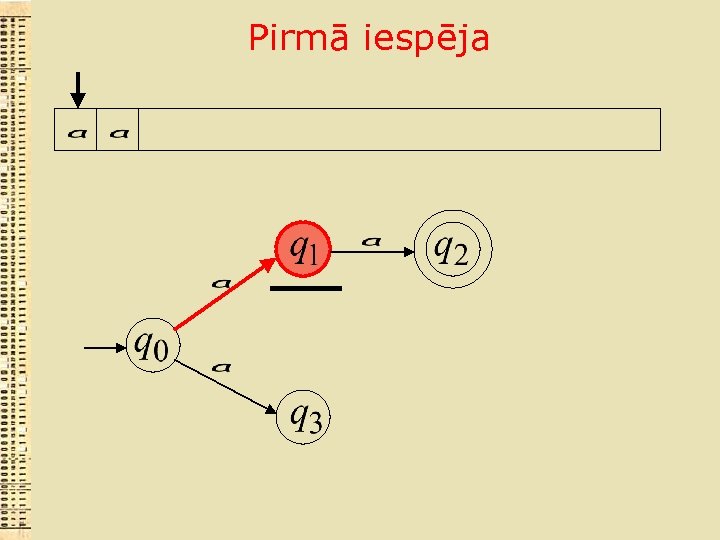 Pirmā iespēja
Pirmā iespēja
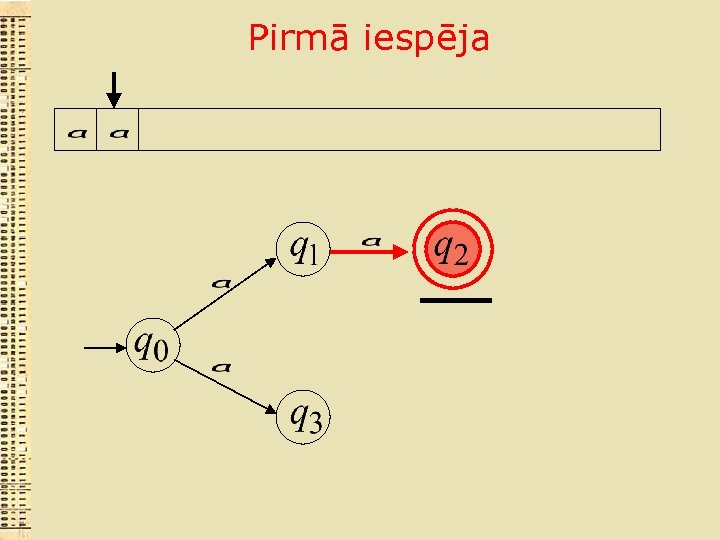 Pirmā iespēja
Pirmā iespēja
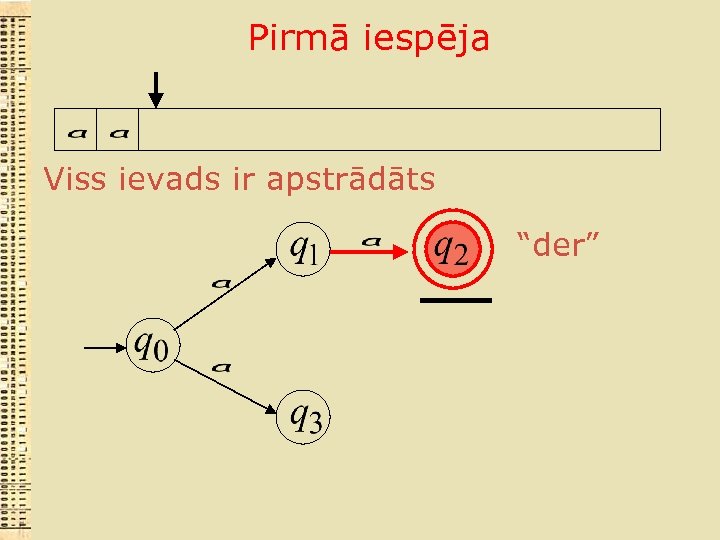 Pirmā iespēja Viss ievads ir apstrādāts “der”
Pirmā iespēja Viss ievads ir apstrādāts “der”
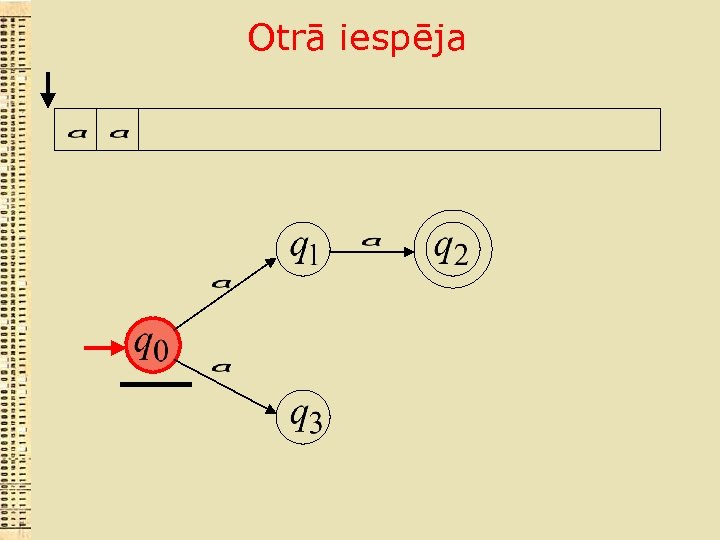 Otrā iespēja
Otrā iespēja
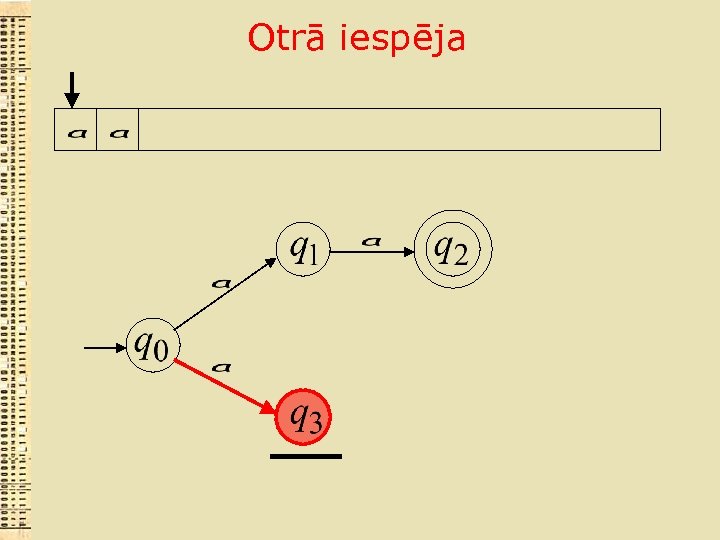 Otrā iespēja
Otrā iespēja
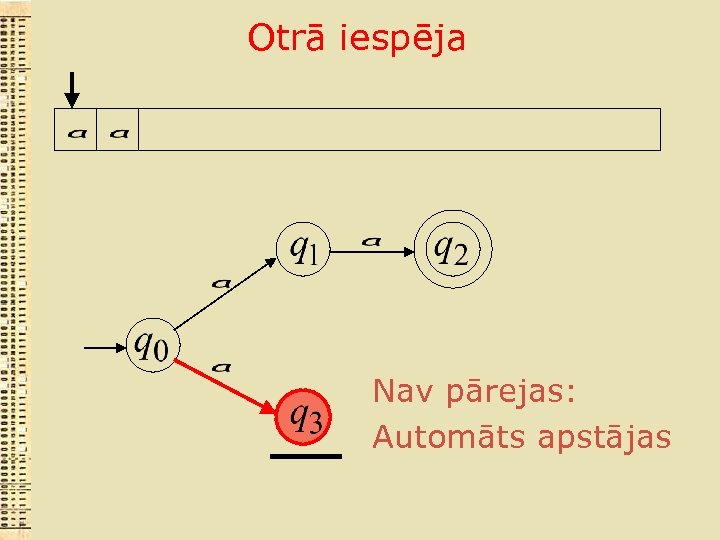 Otrā iespēja Nav pārejas: Automāts apstājas
Otrā iespēja Nav pārejas: Automāts apstājas
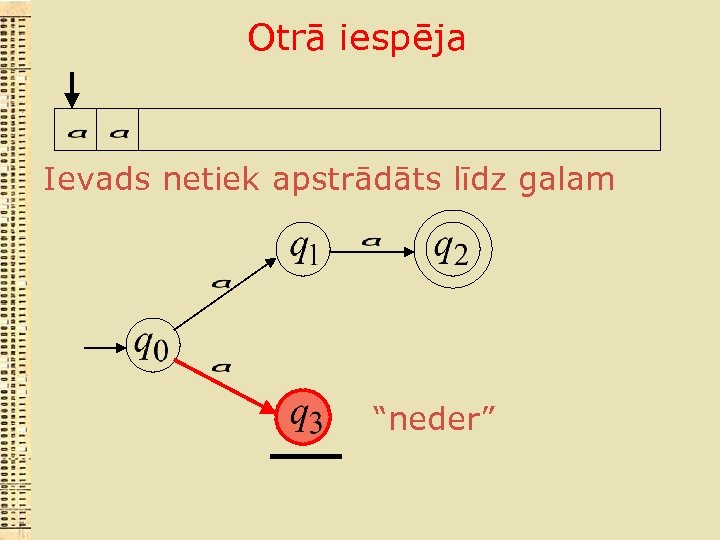 Otrā iespēja Ievads netiek apstrādāts līdz galam “neder”
Otrā iespēja Ievads netiek apstrādāts līdz galam “neder”
 GNA akceptē virkni, ja ir tāda GNA darbību virkne, kas noved pie šīs virknes akceptēšanas. Viss ievads ir apstrādāts un automāts ir beigu stāvoklī.
GNA akceptē virkni, ja ir tāda GNA darbību virkne, kas noved pie šīs virknes akceptēšanas. Viss ievads ir apstrādāts un automāts ir beigu stāvoklī.
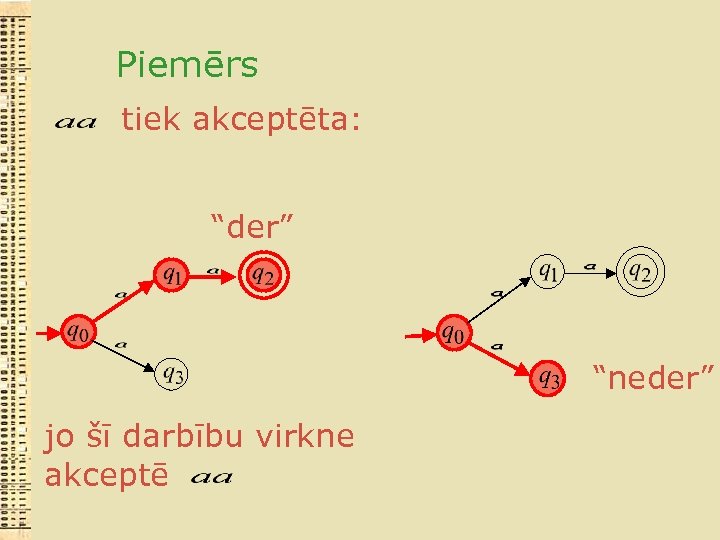 Piemērs tiek akceptēta: “der” “neder” jo šī darbību virkne akceptē
Piemērs tiek akceptēta: “der” “neder” jo šī darbību virkne akceptē
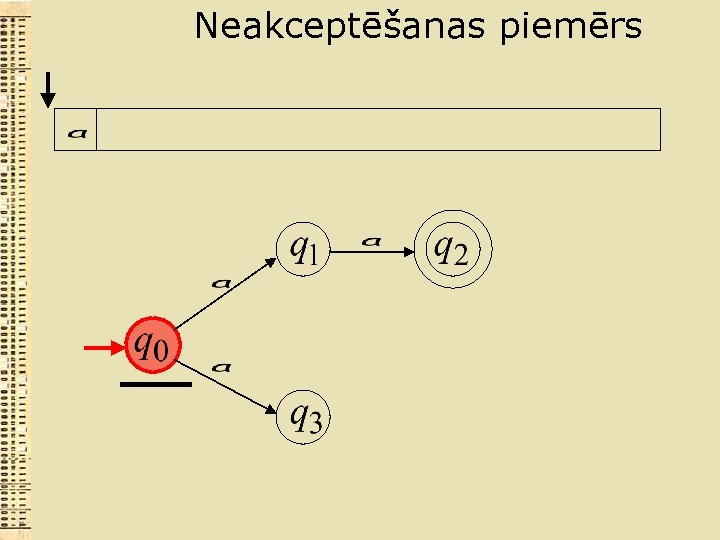 Neakceptēšanas piemērs
Neakceptēšanas piemērs
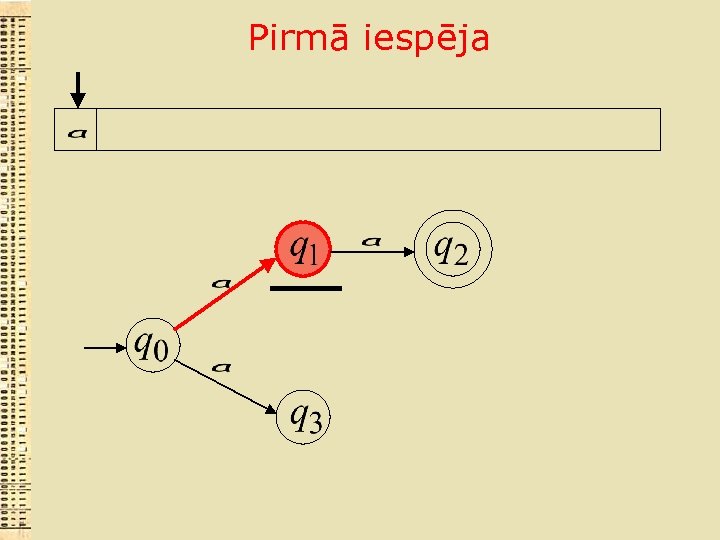 Pirmā iespēja
Pirmā iespēja
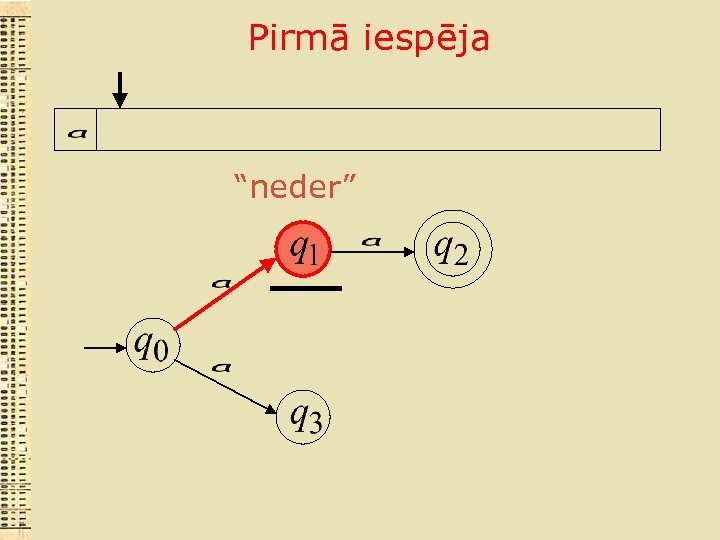 Pirmā iespēja “neder”
Pirmā iespēja “neder”
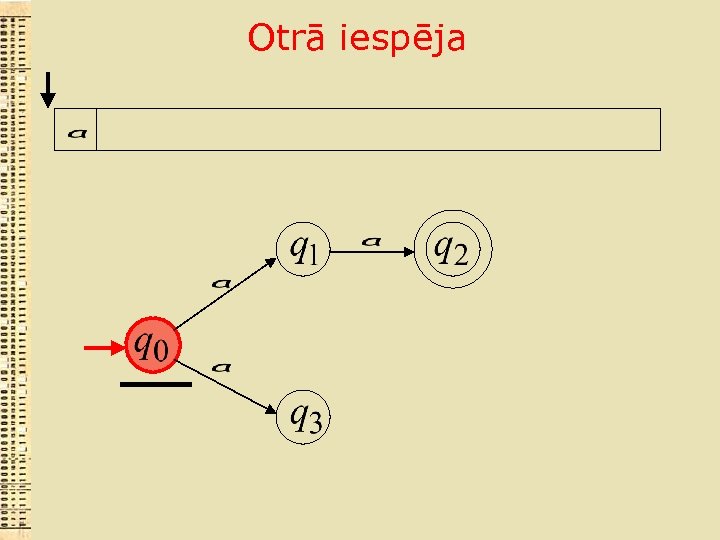 Otrā iespēja
Otrā iespēja
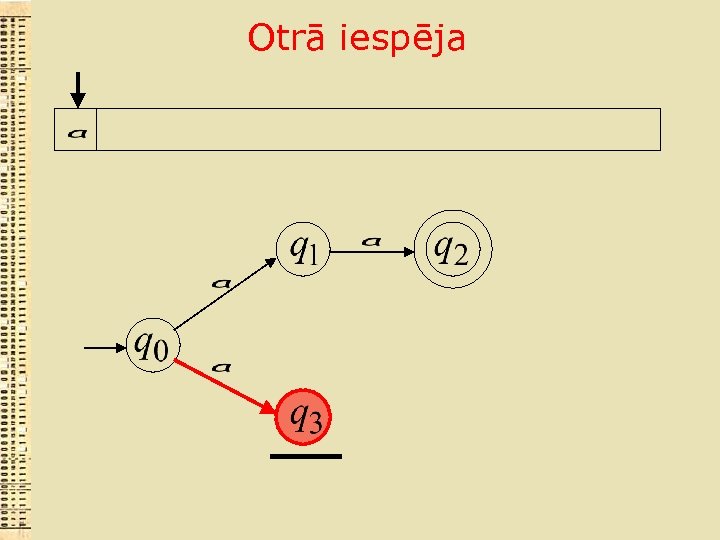 Otrā iespēja
Otrā iespēja
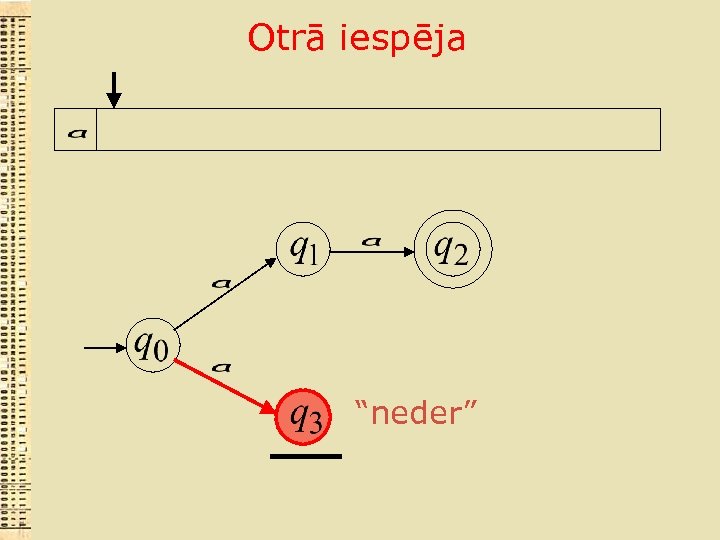 Otrā iespēja “neder”
Otrā iespēja “neder”
 GNA neakceptē virkni, ja neviena GNA darbību virkne neakceptē šo virkni • Viss ievads ir apstrādāts un automāts nav beigu stāvoklī • Ievads nevar tikt apstrādāts, jo nav atbilstošas pārejas
GNA neakceptē virkni, ja neviena GNA darbību virkne neakceptē šo virkni • Viss ievads ir apstrādāts un automāts nav beigu stāvoklī • Ievads nevar tikt apstrādāts, jo nav atbilstošas pārejas
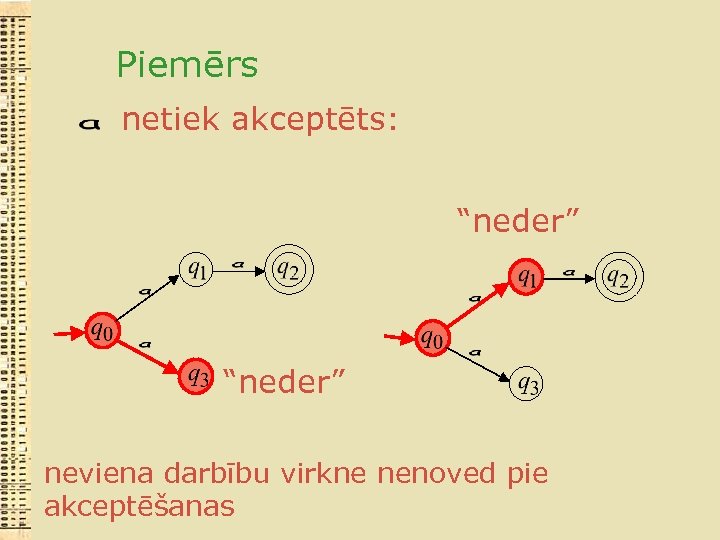 Piemērs netiek akceptēts: “neder” neviena darbību virkne nenoved pie akceptēšanas
Piemērs netiek akceptēts: “neder” neviena darbību virkne nenoved pie akceptēšanas
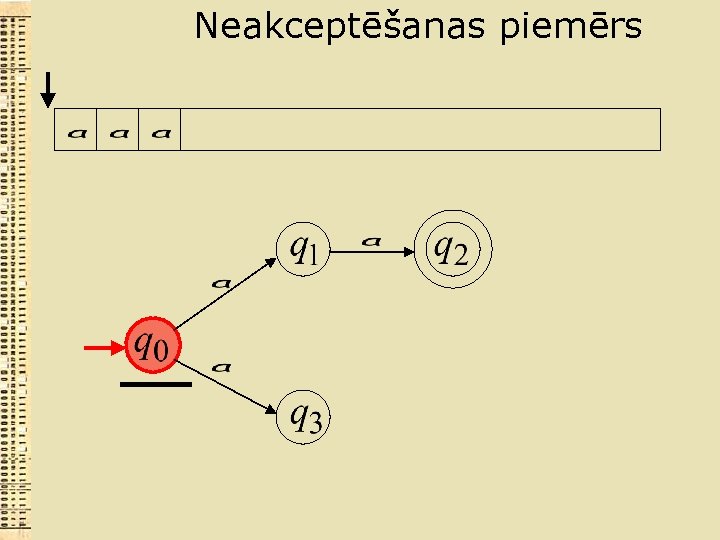 Neakceptēšanas piemērs
Neakceptēšanas piemērs
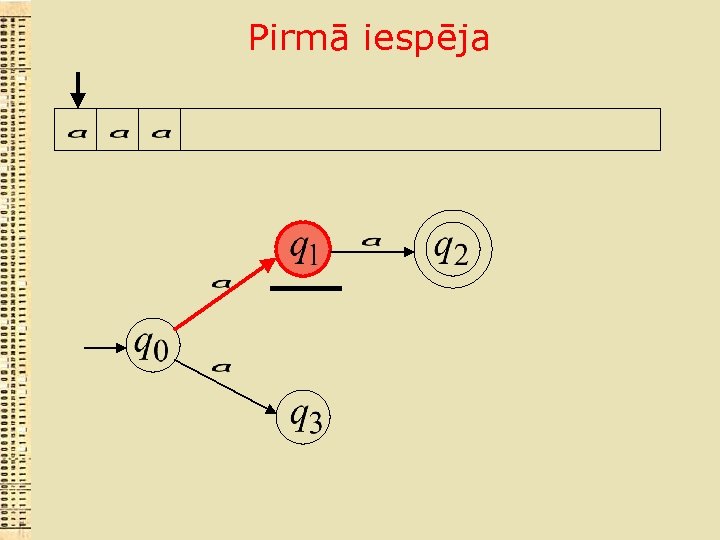 Pirmā iespēja
Pirmā iespēja
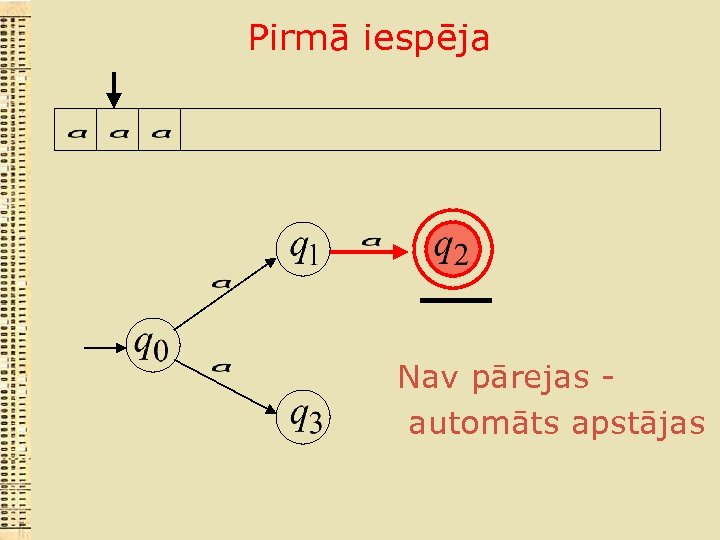 Pirmā iespēja Nav pārejas automāts apstājas
Pirmā iespēja Nav pārejas automāts apstājas
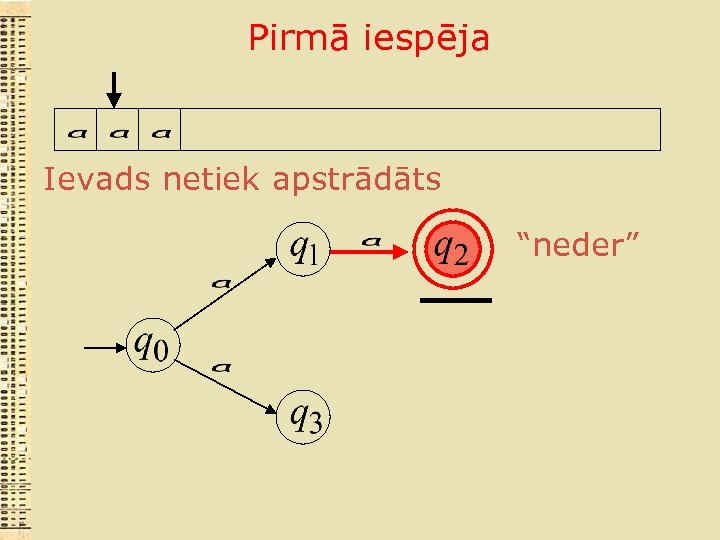 Pirmā iespēja Ievads netiek apstrādāts “neder”
Pirmā iespēja Ievads netiek apstrādāts “neder”
 Otrā iespēja
Otrā iespēja
 Otrā iespēja
Otrā iespēja
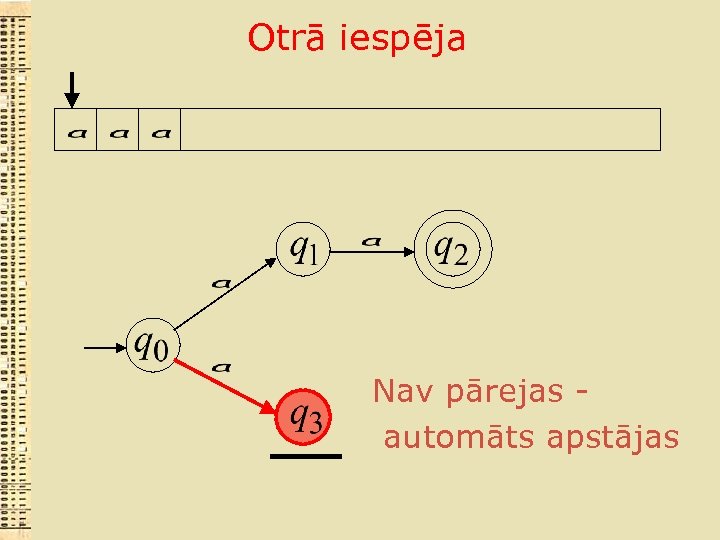 Otrā iespēja Nav pārejas automāts apstājas
Otrā iespēja Nav pārejas automāts apstājas
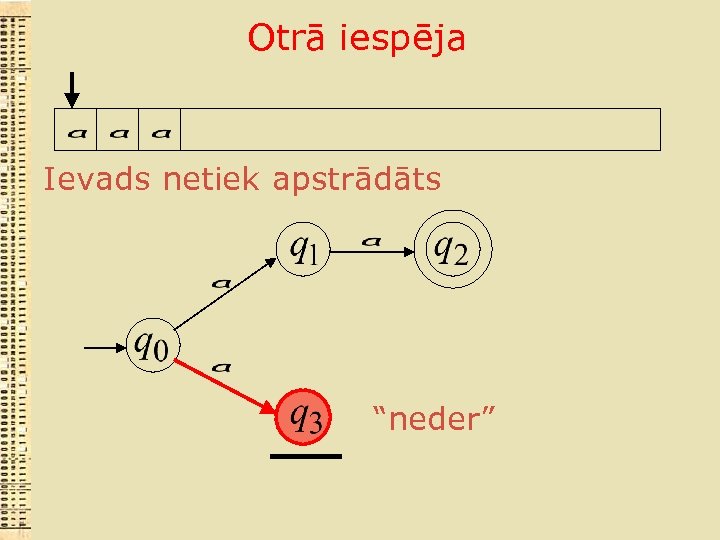 Otrā iespēja Ievads netiek apstrādāts “neder”
Otrā iespēja Ievads netiek apstrādāts “neder”
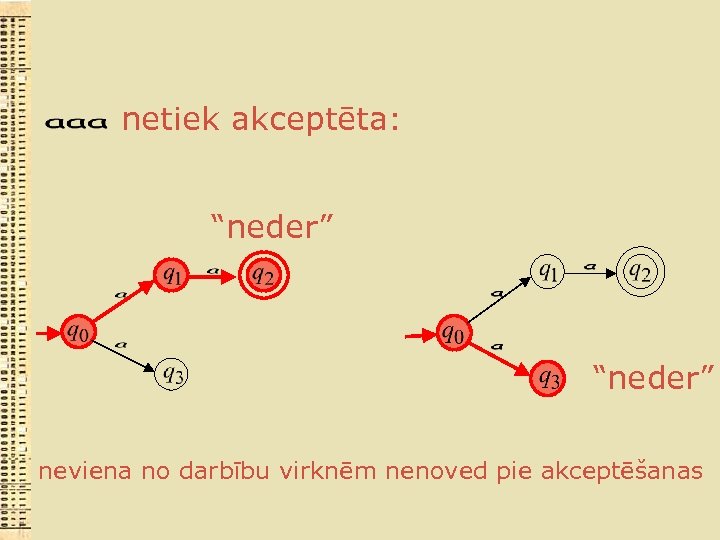 netiek akceptēta: “neder” neviena no darbību virknēm nenoved pie akceptēšanas
netiek akceptēta: “neder” neviena no darbību virknēm nenoved pie akceptēšanas
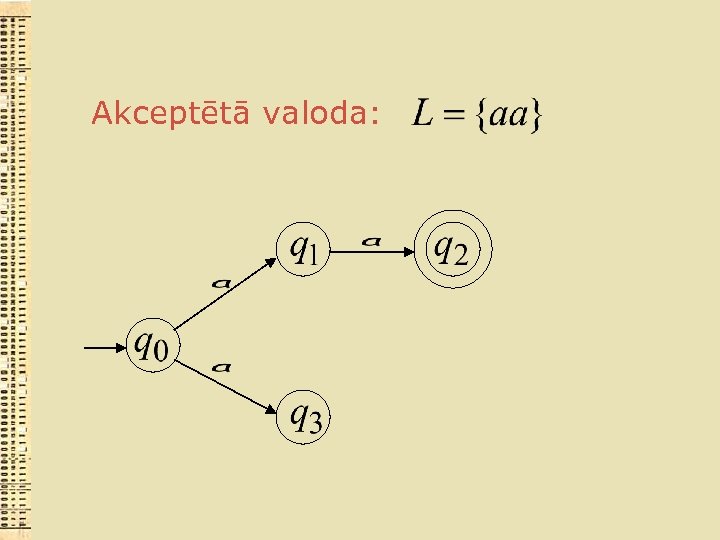 Akceptētā valoda:
Akceptētā valoda:
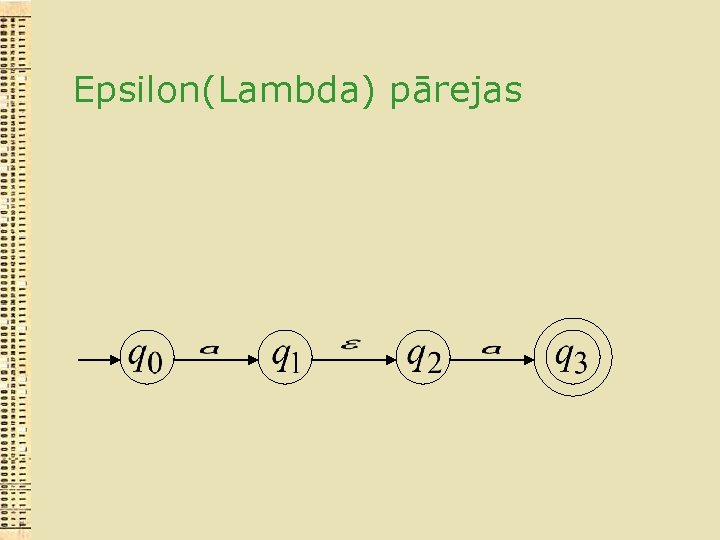 Epsilon(Lambda) pārejas
Epsilon(Lambda) pārejas
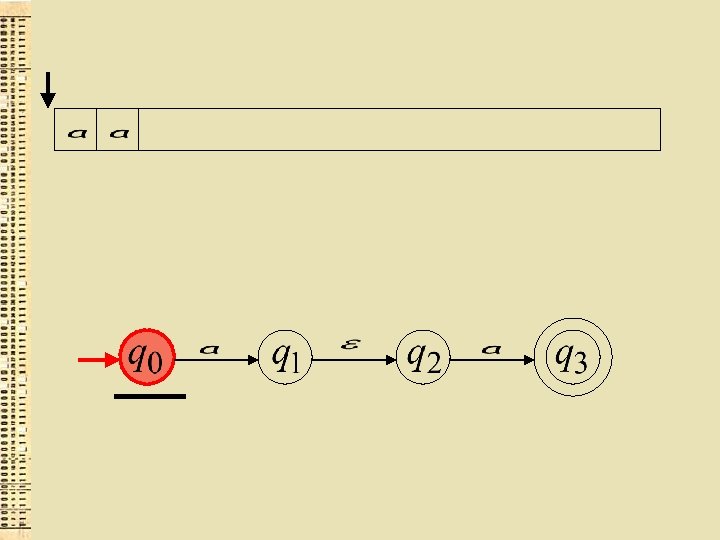
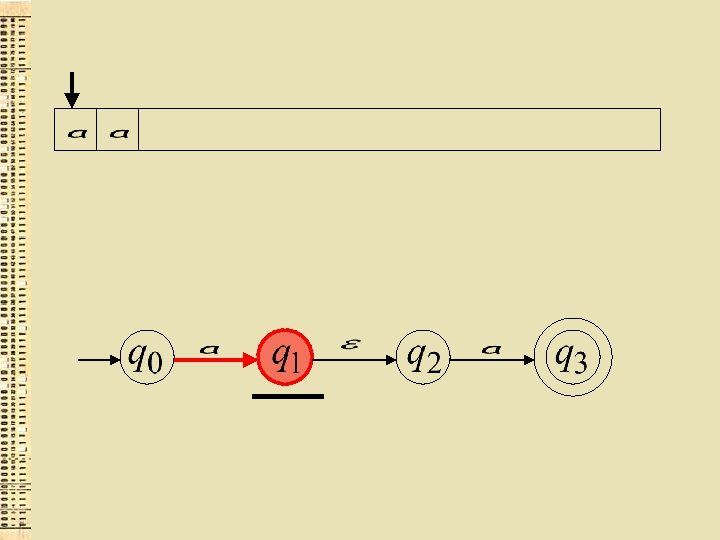
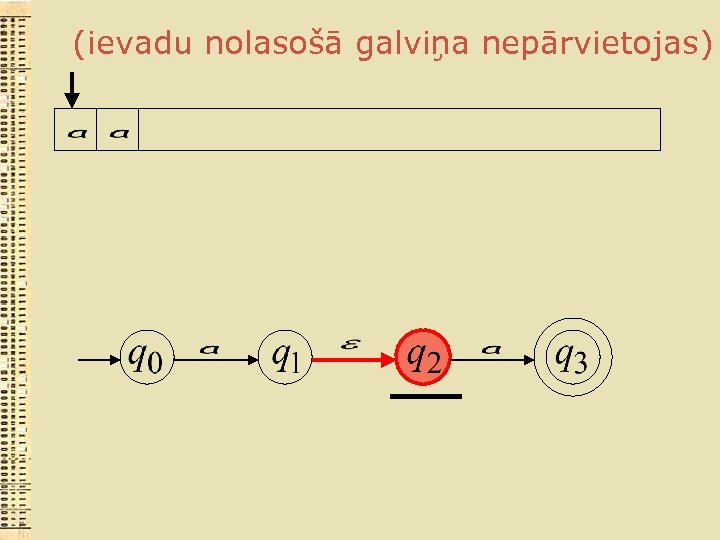 (ievadu nolasošā galviņa nepārvietojas)
(ievadu nolasošā galviņa nepārvietojas)
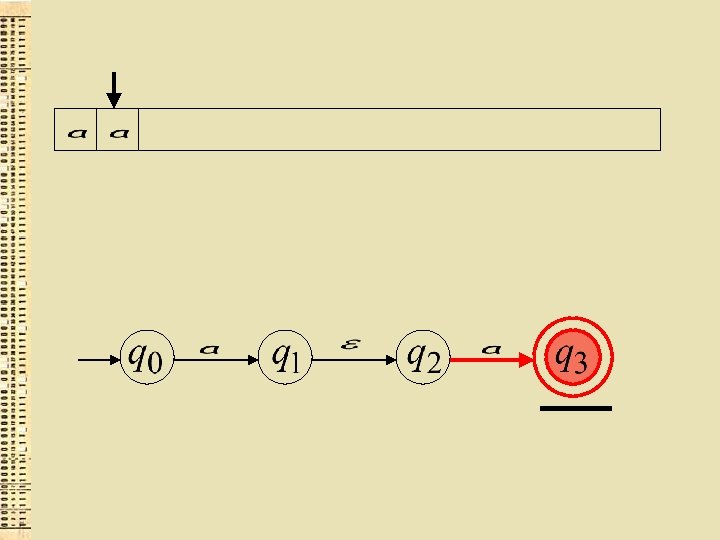
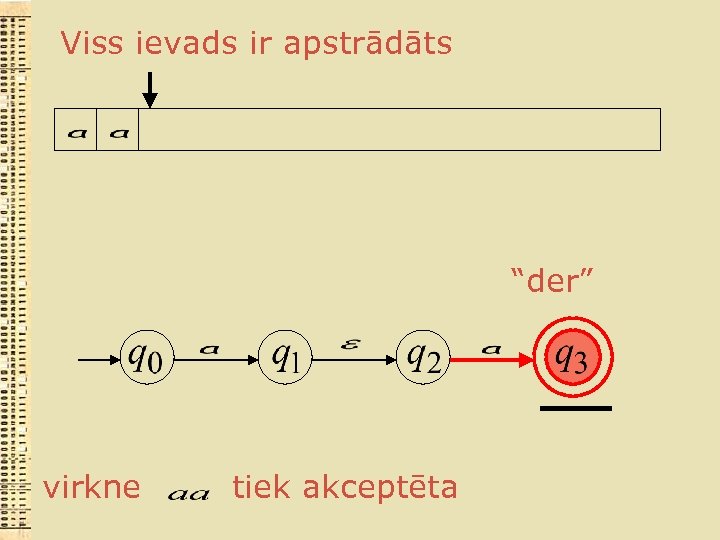 Viss ievads ir apstrādāts “der” virkne tiek akceptēta
Viss ievads ir apstrādāts “der” virkne tiek akceptēta
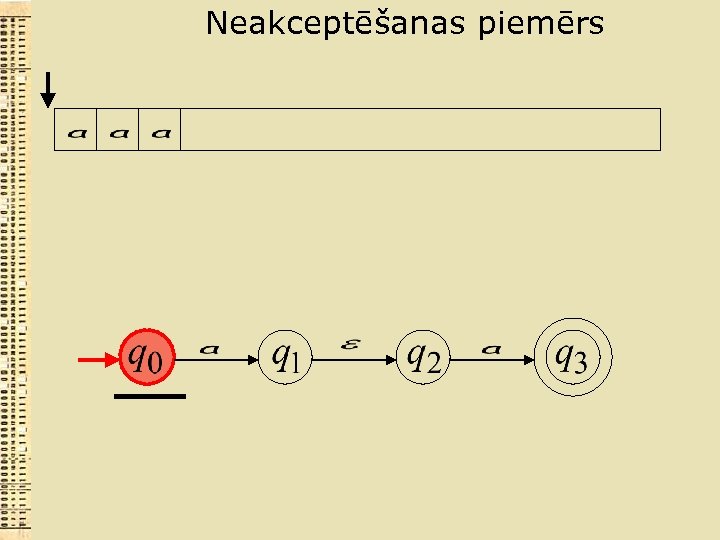 Neakceptēšanas piemērs
Neakceptēšanas piemērs
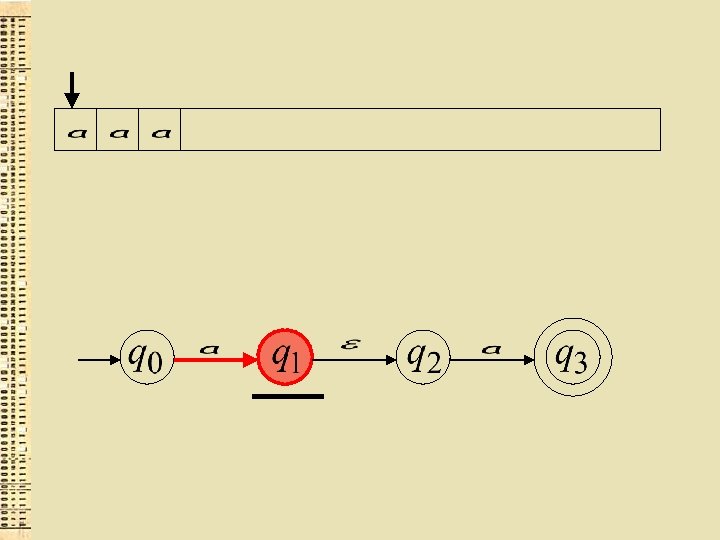
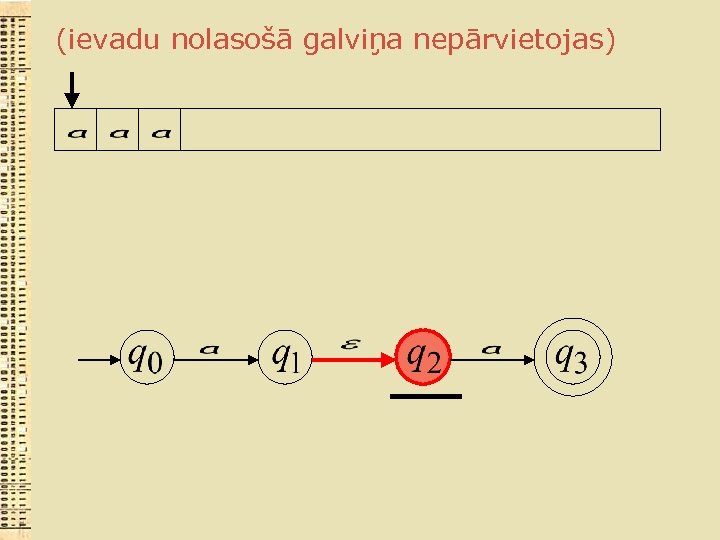 (ievadu nolasošā galviņa nepārvietojas)
(ievadu nolasošā galviņa nepārvietojas)
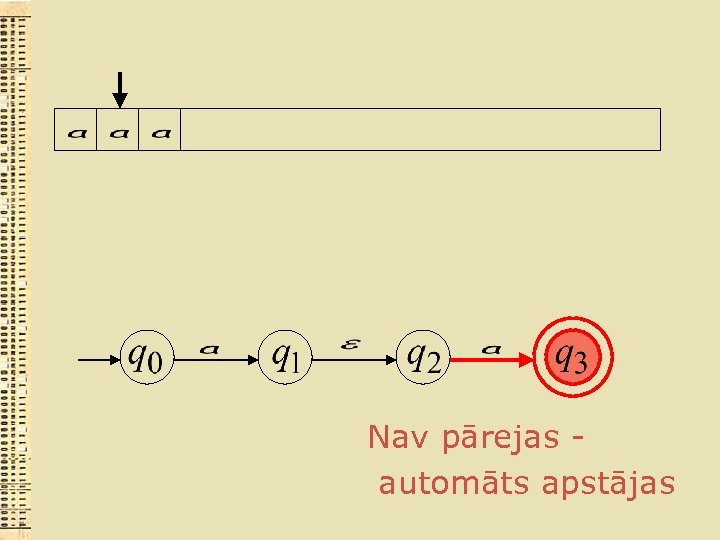 Nav pārejas automāts apstājas
Nav pārejas automāts apstājas
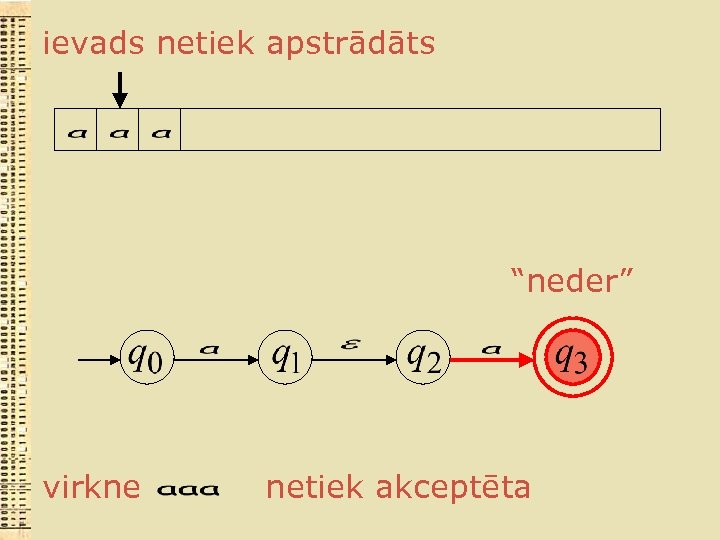 ievads netiek apstrādāts “neder” virkne netiek akceptēta
ievads netiek apstrādāts “neder” virkne netiek akceptēta
 Akceptētā valoda:
Akceptētā valoda:
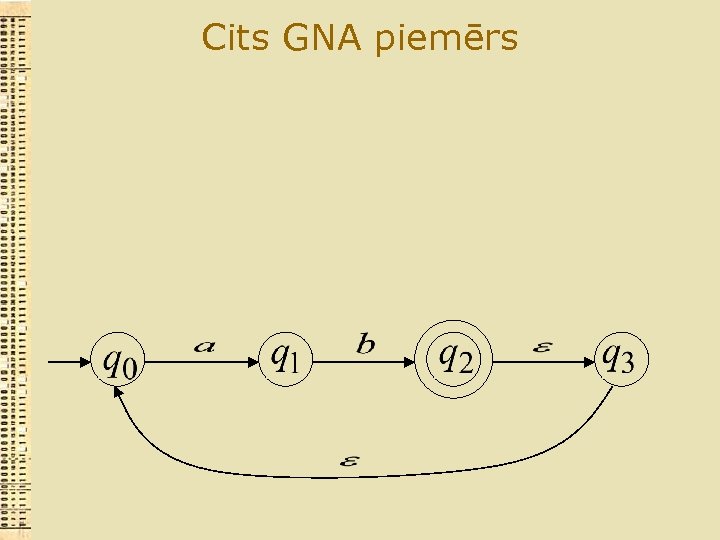 Cits GNA piemērs
Cits GNA piemērs
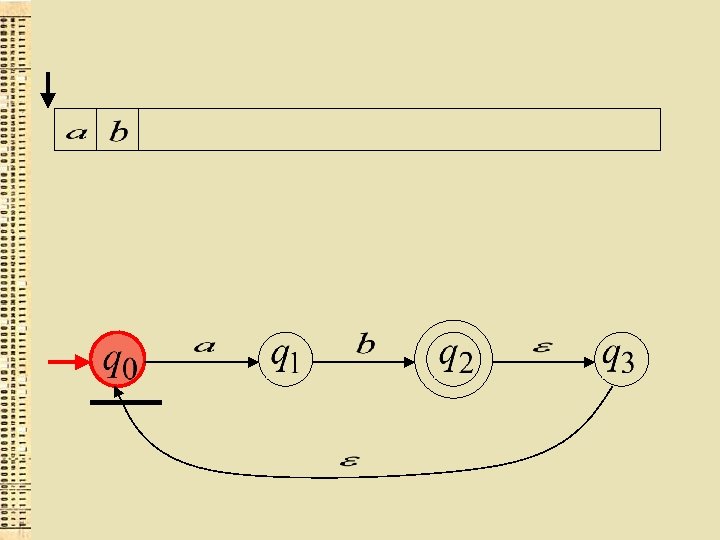
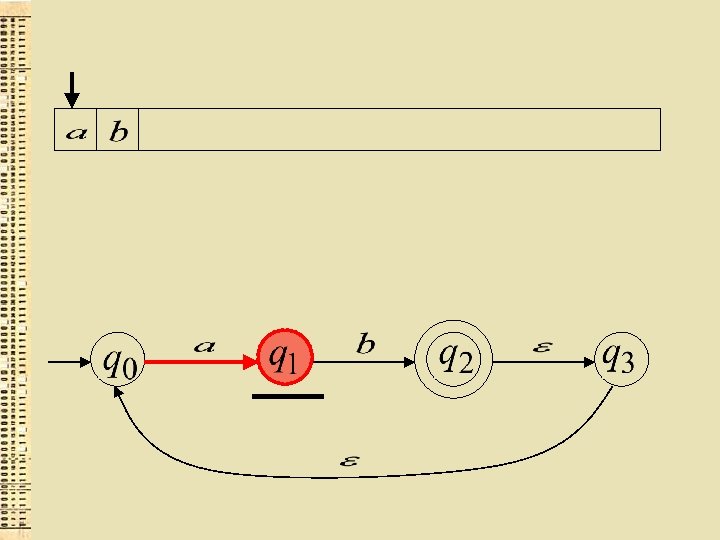
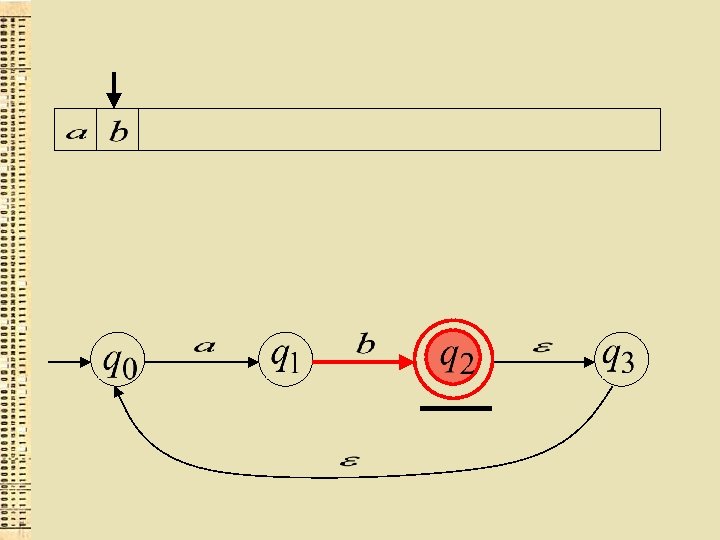
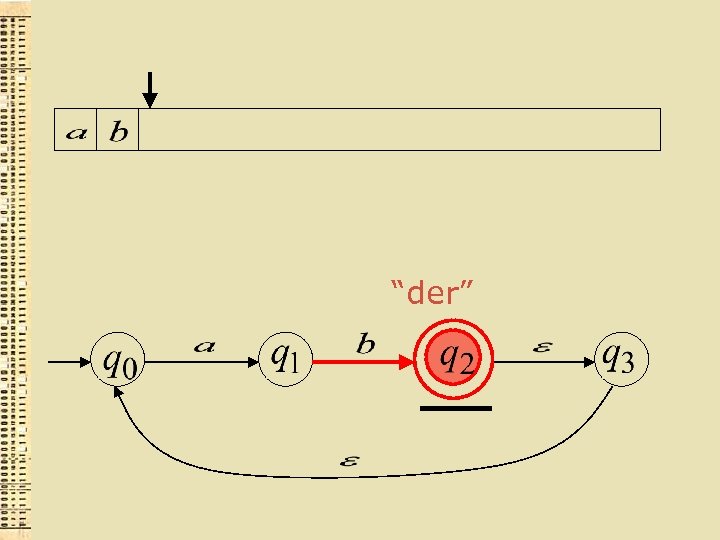 “der”
“der”
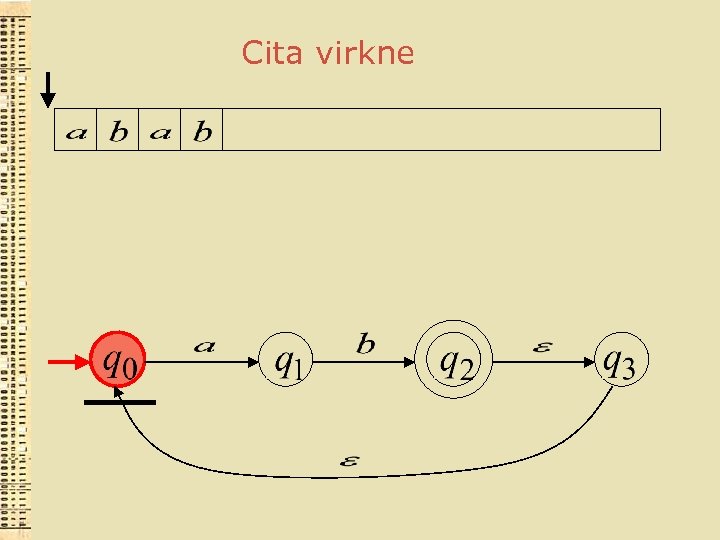 Cita virkne
Cita virkne
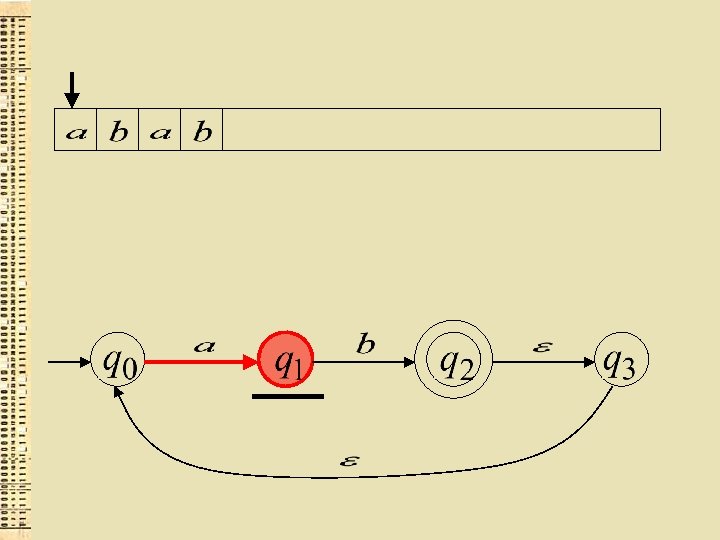
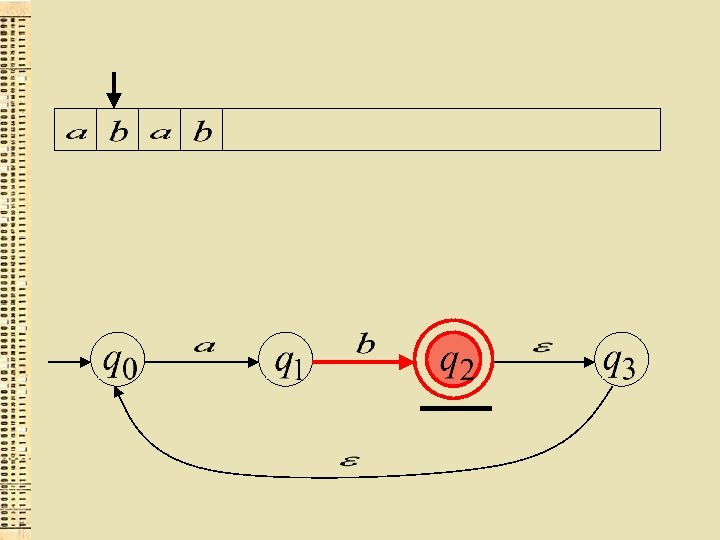

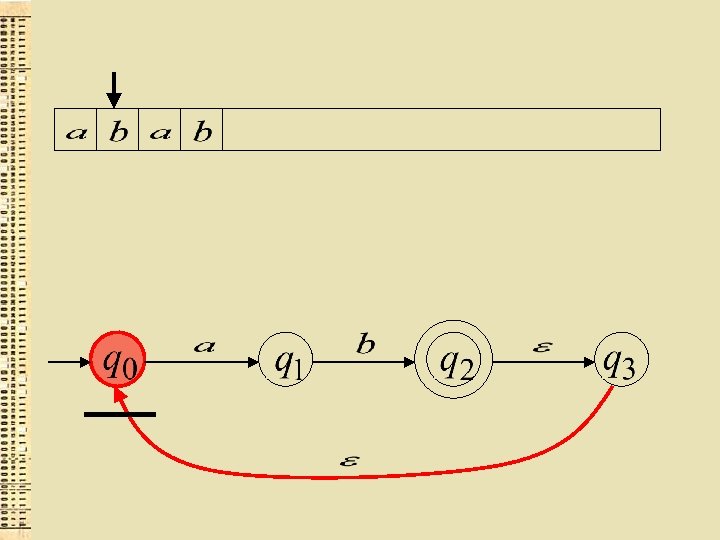
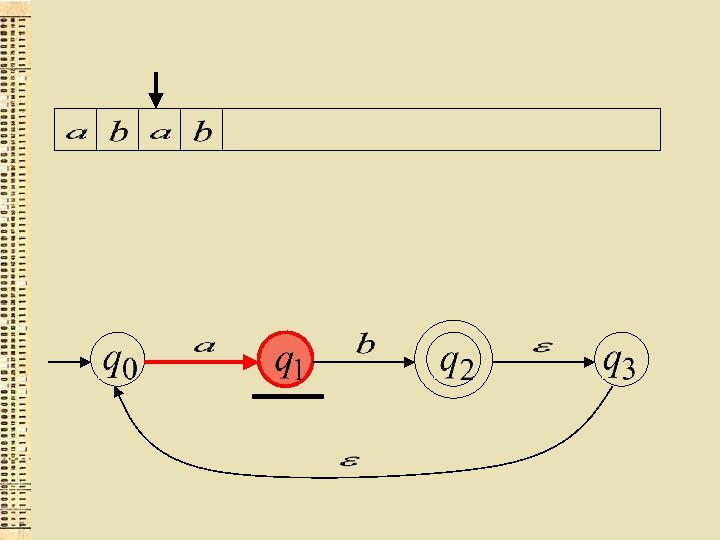
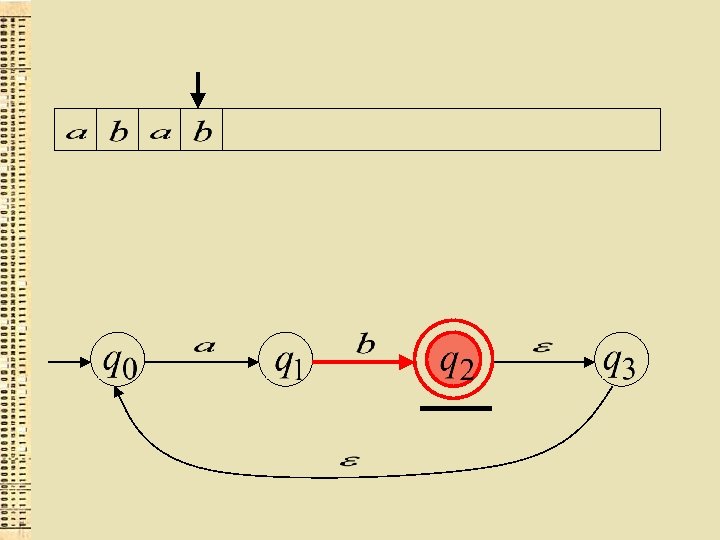
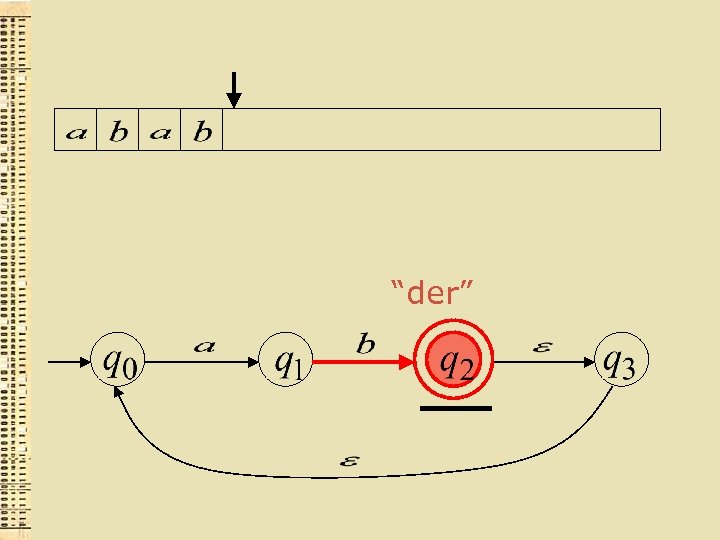 “der”
“der”
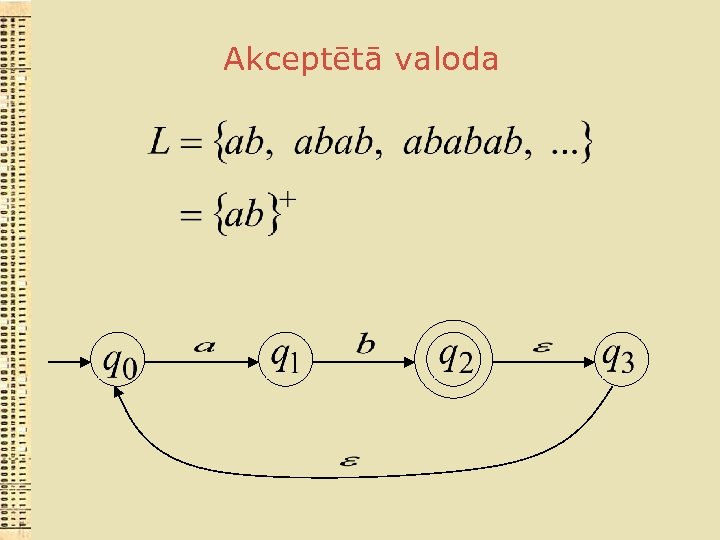 Akceptētā valoda
Akceptētā valoda
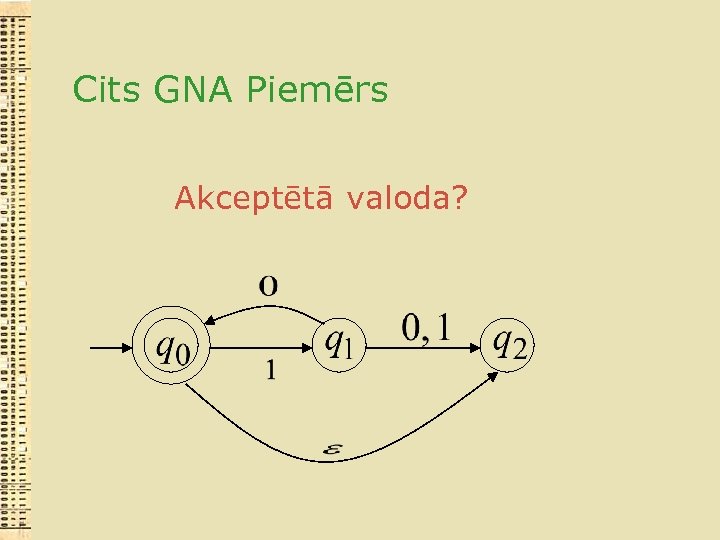 Cits GNA Piemērs Akceptētā valoda?
Cits GNA Piemērs Akceptētā valoda?
 Akceptētā valoda
Akceptētā valoda
 Piezīmes: • simbols nekad neparādās uz ievada lentas • “Ekstrēmie” automāti:
Piezīmes: • simbols nekad neparādās uz ievada lentas • “Ekstrēmie” automāti:
 GNA formālā definīcija Stāvokļu kopa, t. i. Ievada alfabēts, t. i. Pārejas funkcija Sākuma stāvoklis Beigu stāvokļi
GNA formālā definīcija Stāvokļu kopa, t. i. Ievada alfabēts, t. i. Pārejas funkcija Sākuma stāvoklis Beigu stāvokļi
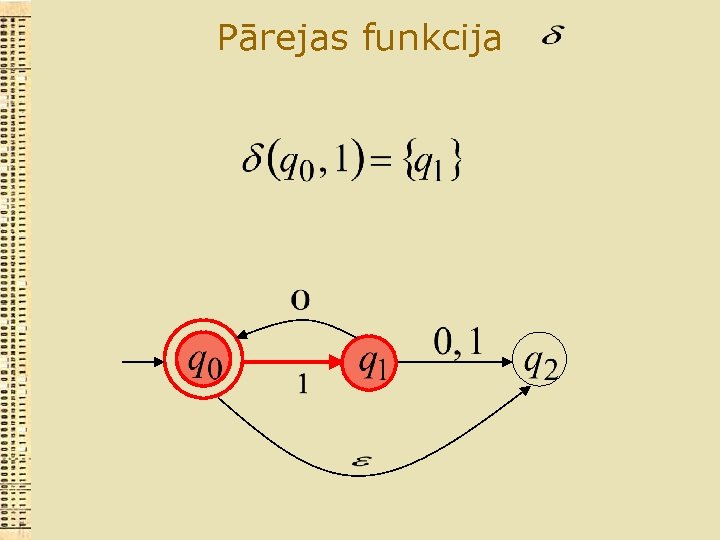 Pārejas funkcija
Pārejas funkcija
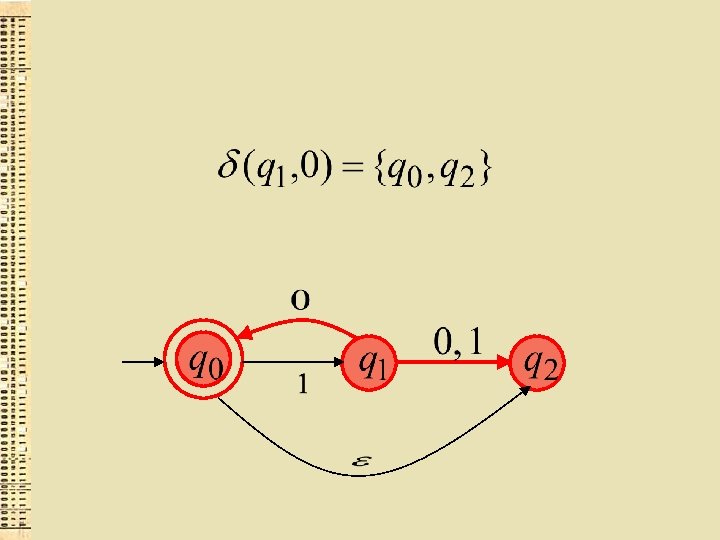
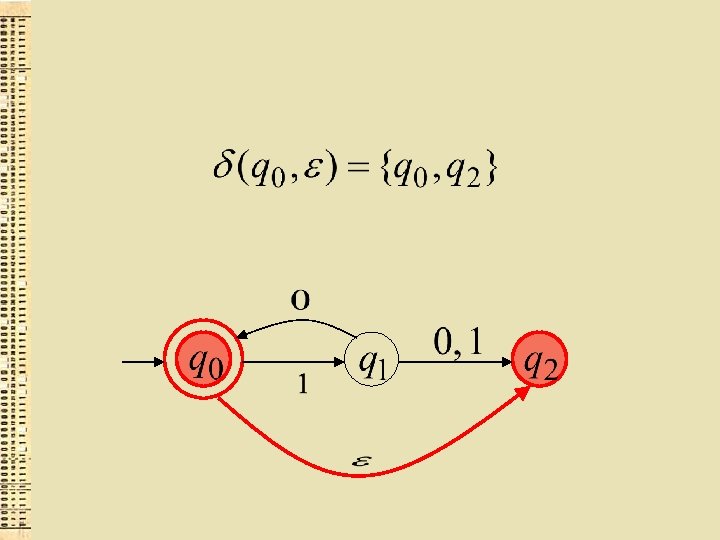
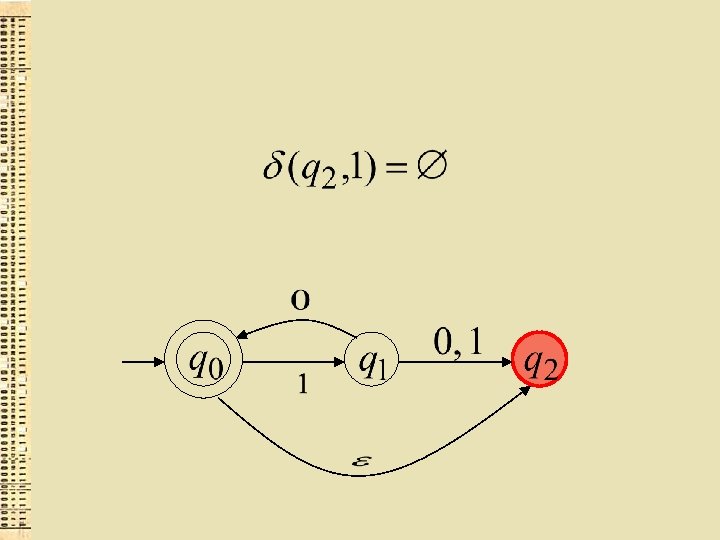
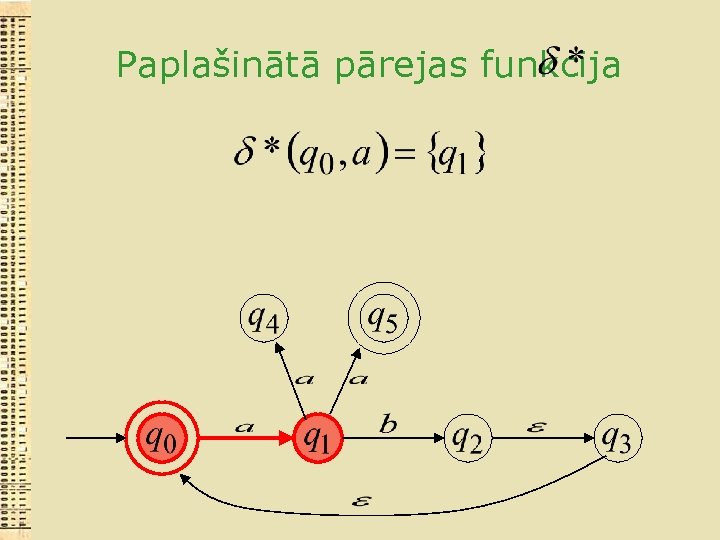 Paplašinātā pārejas funkcija
Paplašinātā pārejas funkcija
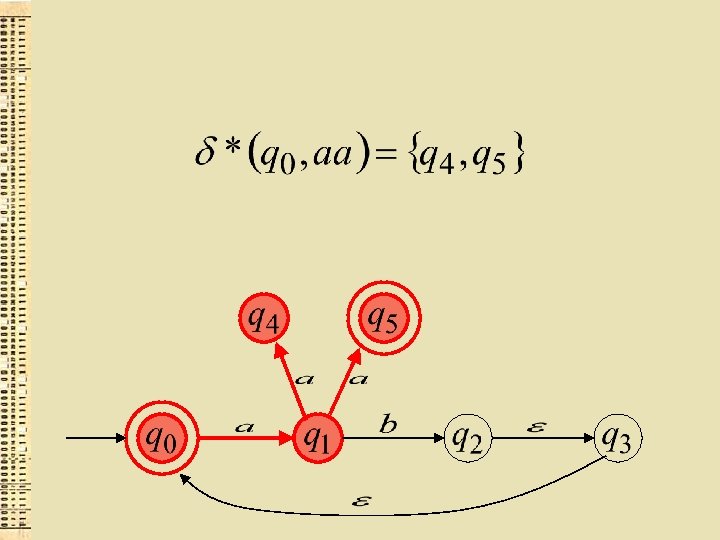
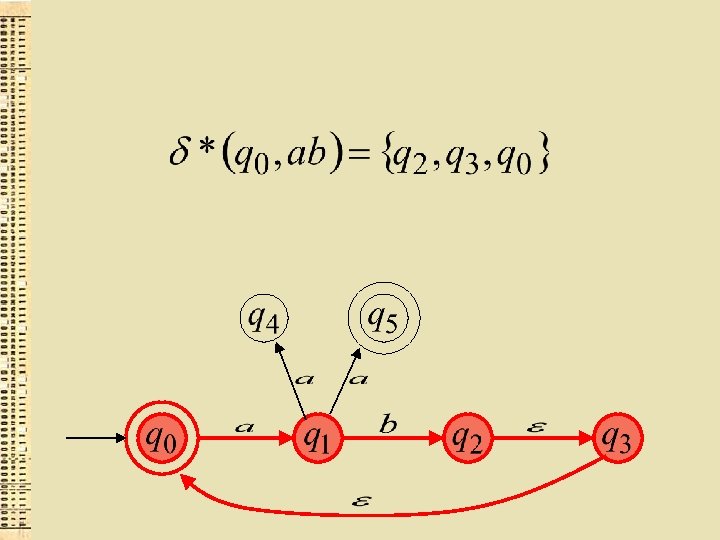
 Formāli tad un tikai tad, ja eksistē maršruts no ar iezīmju virkni uz
Formāli tad un tikai tad, ja eksistē maršruts no ar iezīmju virkni uz
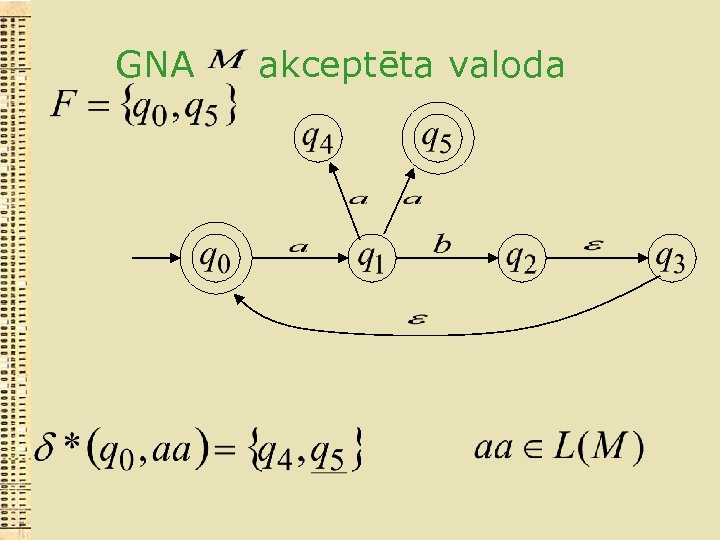 GNA akceptēta valoda
GNA akceptēta valoda
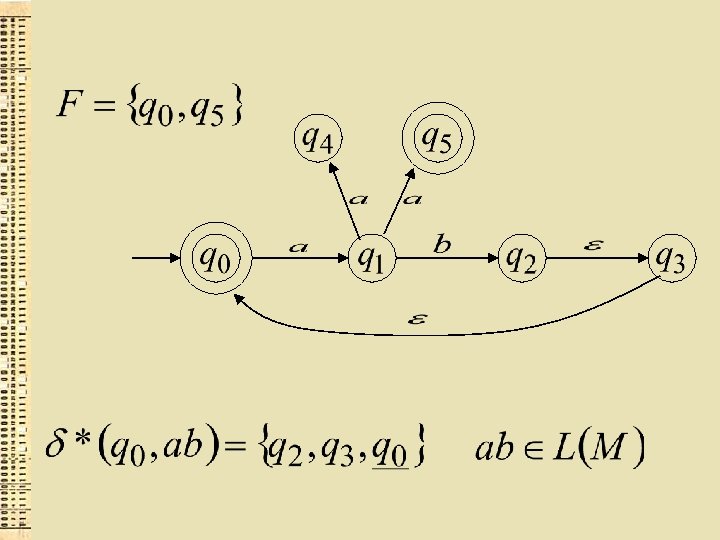
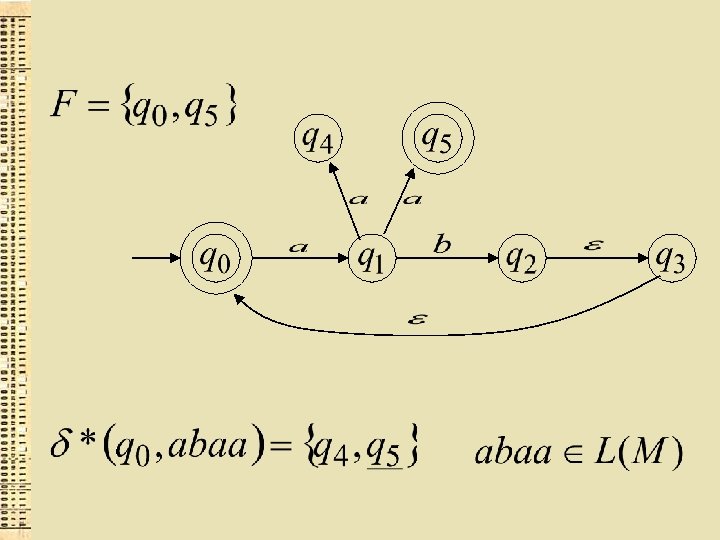
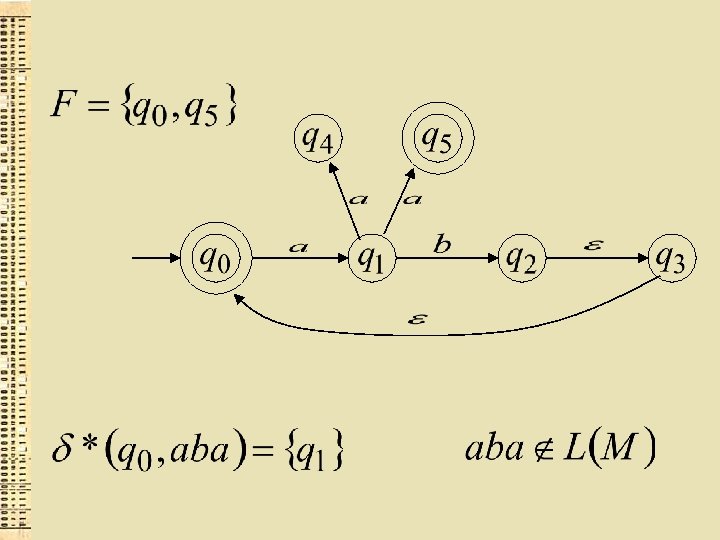
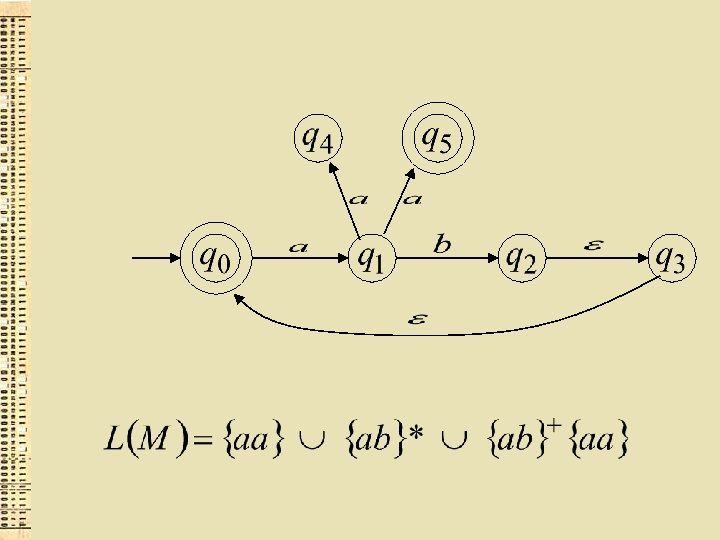
 Formāli GNA akceptēta valoda ir: kur un starp tiem ir kāds beigu stāvoklis
Formāli GNA akceptēta valoda ir: kur un starp tiem ir kāds beigu stāvoklis
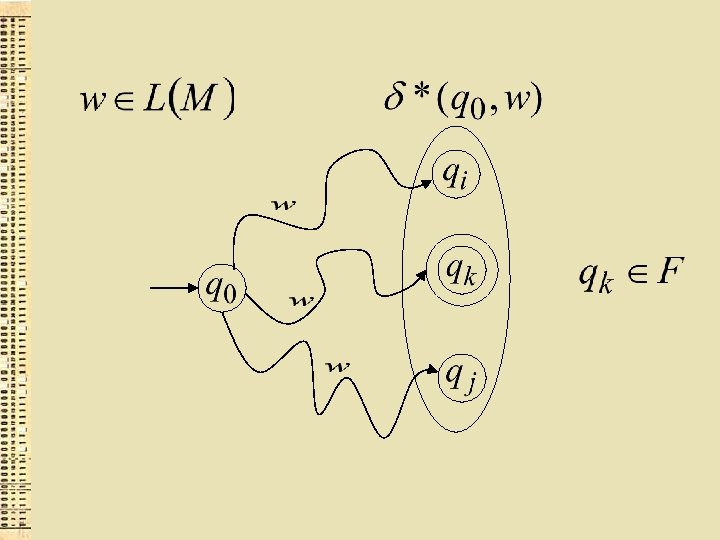
 Ja GNA akceptē regulāras valodas un jebkuru regulāru valodu var aprakstīt ar GNA, tad no jebkuras regulāras izteiksmes vajadzētu varēt izveidot GNA un no jebkura GNA – regulāru izteiksmi. Vajadzētu parādīt: • kā no jebkuras regulāras izteiksmes iegūt atbilstošo GNA • kā jebkuram GNA atrast atbilstošo regulāro izteiksmi
Ja GNA akceptē regulāras valodas un jebkuru regulāru valodu var aprakstīt ar GNA, tad no jebkuras regulāras izteiksmes vajadzētu varēt izveidot GNA un no jebkura GNA – regulāru izteiksmi. Vajadzētu parādīt: • kā no jebkuras regulāras izteiksmes iegūt atbilstošo GNA • kā jebkuram GNA atrast atbilstošo regulāro izteiksmi
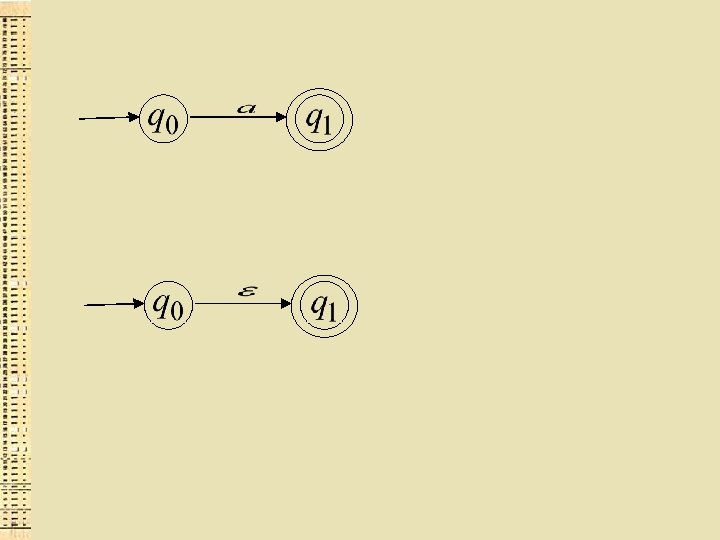
 No regulāras izteiksmes iegūt atbilstošo GNA (Tompsona konstrukcija) Dota regulāra izteiksme r alfabētā Σ, jākonstruē GNA, kas apraksta valodu L(r). Vispirms parāda, kā konstruēt vienkāršus GNA visiem alfabēta simboliem un tukšajai virknei.
No regulāras izteiksmes iegūt atbilstošo GNA (Tompsona konstrukcija) Dota regulāra izteiksme r alfabētā Σ, jākonstruē GNA, kas apraksta valodu L(r). Vispirms parāda, kā konstruēt vienkāršus GNA visiem alfabēta simboliem un tukšajai virknei.
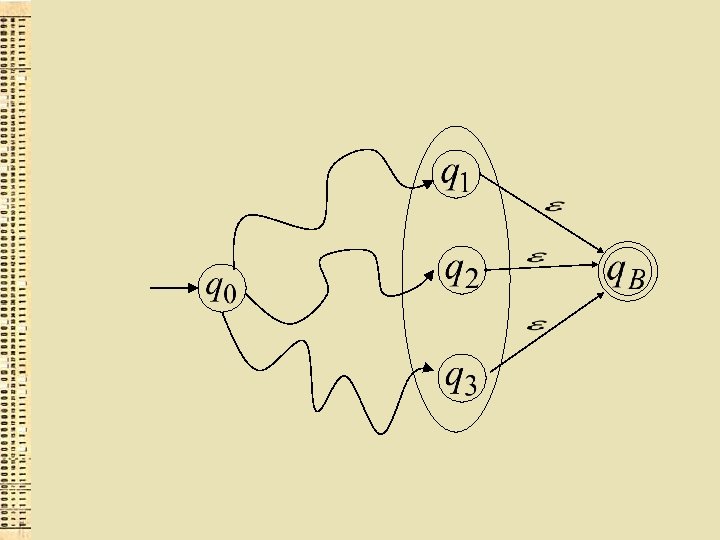
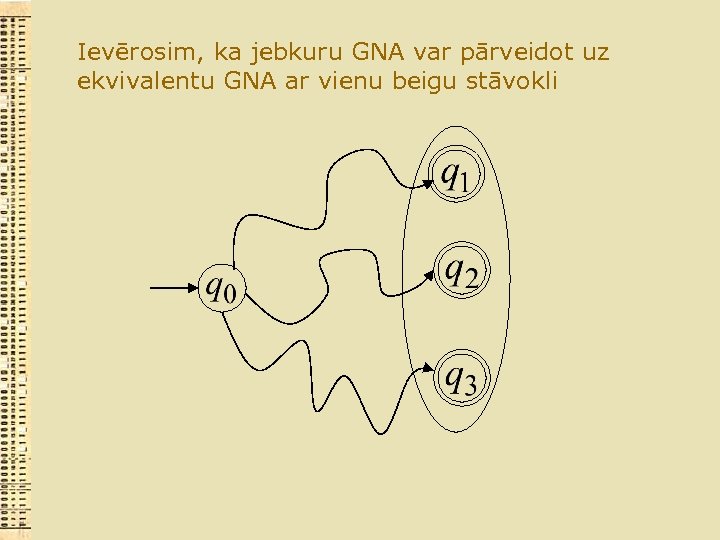 Ievērosim, ka jebkuru GNA var pārveidot uz ekvivalentu GNA ar vienu beigu stāvokli
Ievērosim, ka jebkuru GNA var pārveidot uz ekvivalentu GNA ar vienu beigu stāvokli
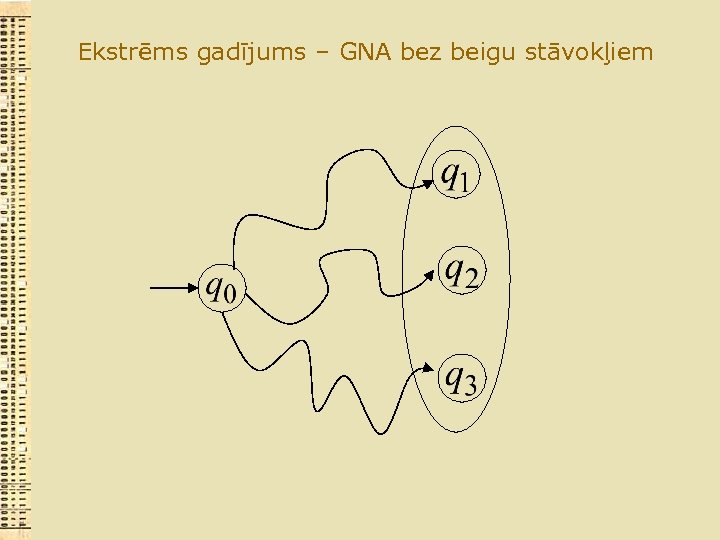 Ekstrēms gadījums – GNA bez beigu stāvokļiem
Ekstrēms gadījums – GNA bez beigu stāvokļiem
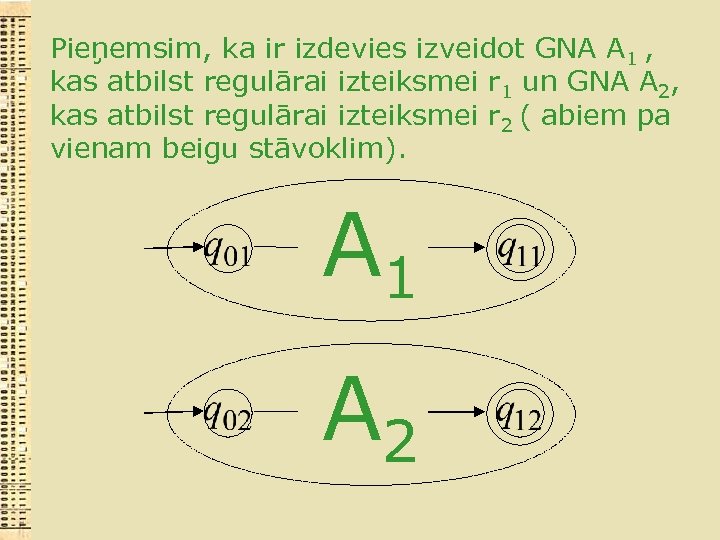 Pieņemsim, ka ir izdevies izveidot GNA A 1 , kas atbilst regulārai izteiksmei r 1 un GNA A 2, kas atbilst regulārai izteiksmei r 2 ( abiem pa vienam beigu stāvoklim). A 1 A 2
Pieņemsim, ka ir izdevies izveidot GNA A 1 , kas atbilst regulārai izteiksmei r 1 un GNA A 2, kas atbilst regulārai izteiksmei r 2 ( abiem pa vienam beigu stāvoklim). A 1 A 2
 Izteiksmei r 1|r 2 būvē GNA :
Izteiksmei r 1|r 2 būvē GNA :
 Izteiksmei r 1|r 2 būvē GNA : A 1 A 2
Izteiksmei r 1|r 2 būvē GNA : A 1 A 2
 Izteiksmei r 1 r 2 būvē GNA :
Izteiksmei r 1 r 2 būvē GNA :
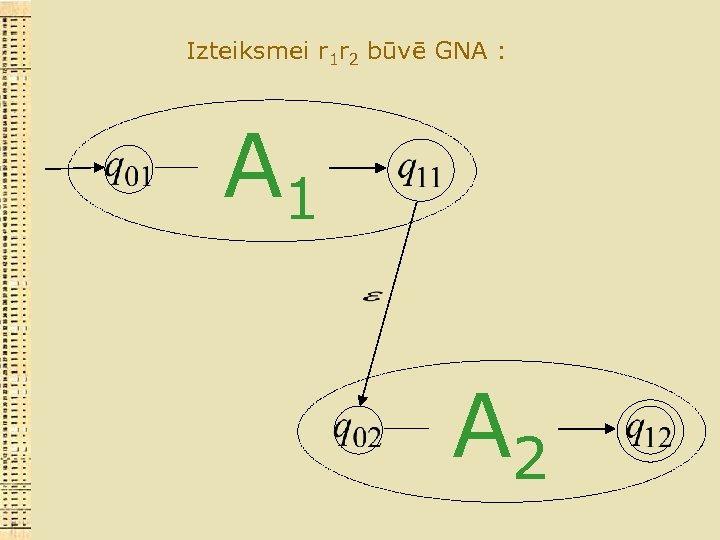 Izteiksmei r 1 r 2 būvē GNA : A 1 A 2
Izteiksmei r 1 r 2 būvē GNA : A 1 A 2
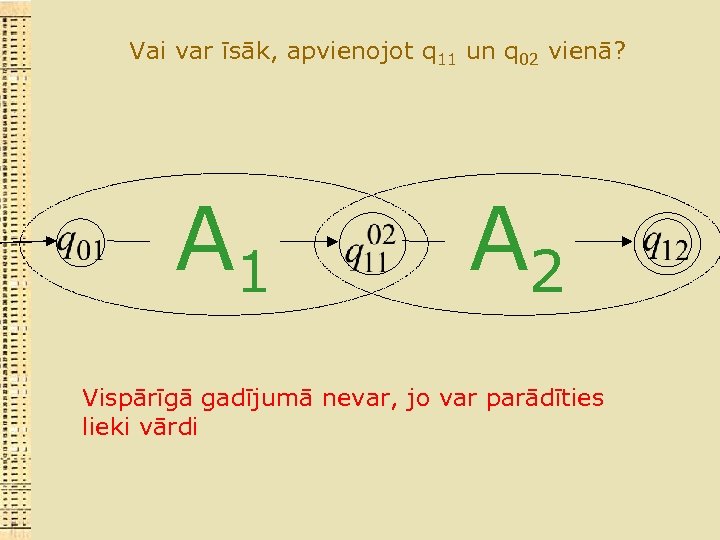 Vai var īsāk, apvienojot q 11 un q 02 vienā? A 1 A 2 Vispārīgā gadījumā nevar, jo var parādīties lieki vārdi
Vai var īsāk, apvienojot q 11 un q 02 vienā? A 1 A 2 Vispārīgā gadījumā nevar, jo var parādīties lieki vārdi
 Izteiksmei r 1* būvē GNA :
Izteiksmei r 1* būvē GNA :
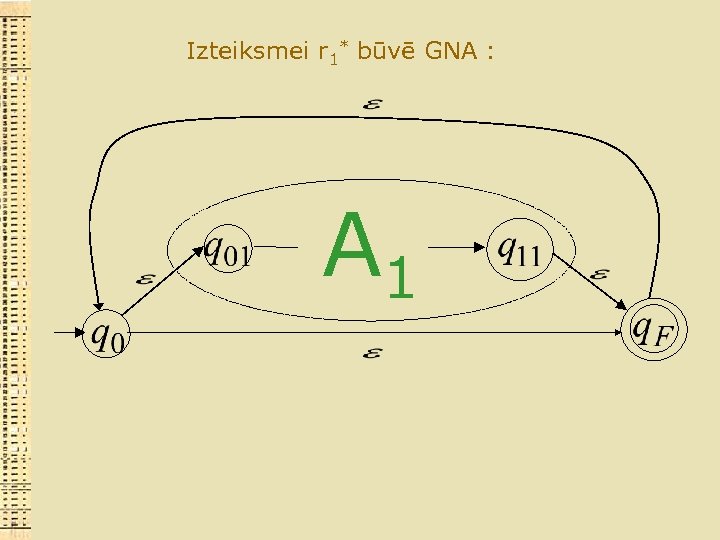 Izteiksmei r 1* būvē GNA : A 1
Izteiksmei r 1* būvē GNA : A 1
 L((r 1)) atbilst A 1
L((r 1)) atbilst A 1
 Piemērs: Dota regulāra izteiksme r=(a|bb)*a*b Uzbūvēt GNA A tā, lai L(A)=L(r) Kā saviem vārdiem aprakstīt šo valodu? Kā izskatītos GNA, ja tas tiktu būvēts uzreiz, nevis formāli no r ?
Piemērs: Dota regulāra izteiksme r=(a|bb)*a*b Uzbūvēt GNA A tā, lai L(A)=L(r) Kā saviem vārdiem aprakstīt šo valodu? Kā izskatītos GNA, ja tas tiktu būvēts uzreiz, nevis formāli no r ?
 Tagad otrā virzienā: kā jebkuram GNA atrast atbilstošo regulāro izteiksmi?
Tagad otrā virzienā: kā jebkuram GNA atrast atbilstošo regulāro izteiksmi?
 Ņemam GNA A, kas akceptē valodu L viens beigu stāvoklis
Ņemam GNA A, kas akceptē valodu L viens beigu stāvoklis
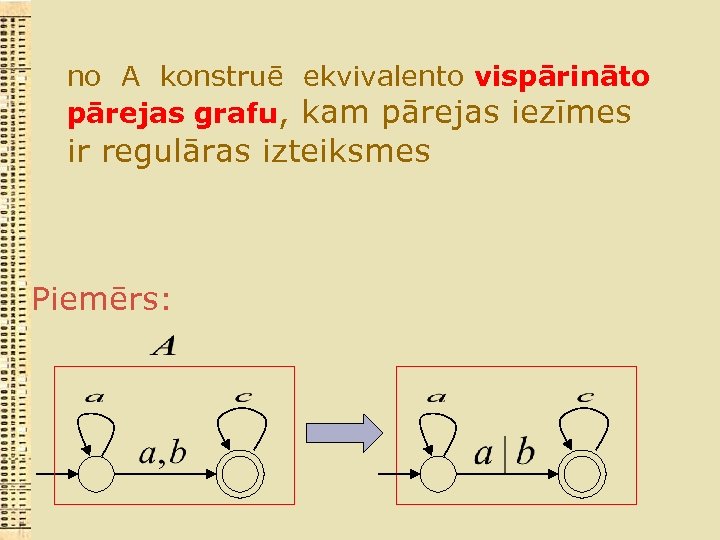 no A konstruē ekvivalento vispārināto pārejas grafu, kam pārejas iezīmes ir regulāras izteiksmes Piemērs:
no A konstruē ekvivalento vispārināto pārejas grafu, kam pārejas iezīmes ir regulāras izteiksmes Piemērs:
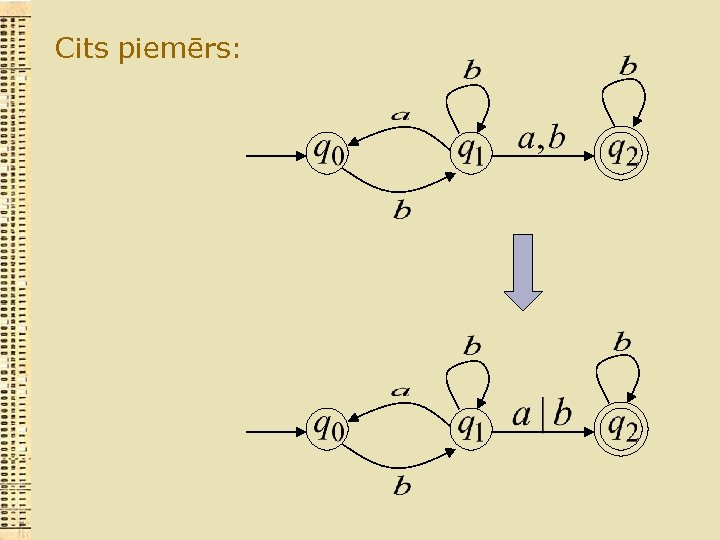 Cits piemērs:
Cits piemērs:
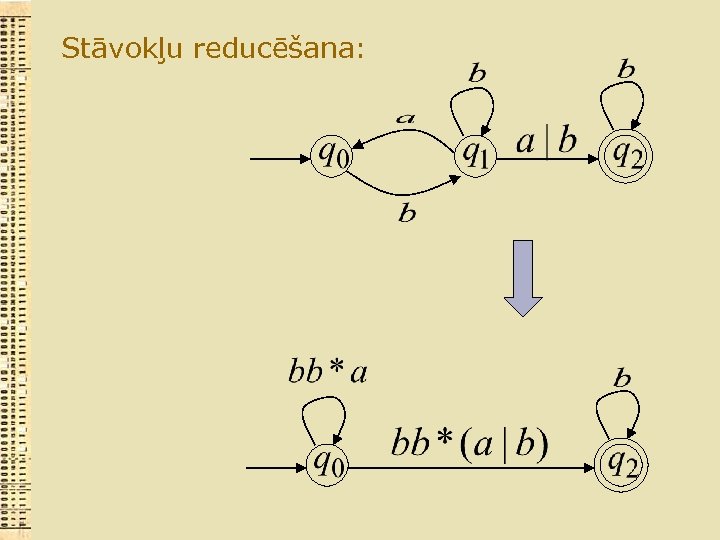 Stāvokļu reducēšana:
Stāvokļu reducēšana:
 Rezultējošā regulārā izteiksme:
Rezultējošā regulārā izteiksme:
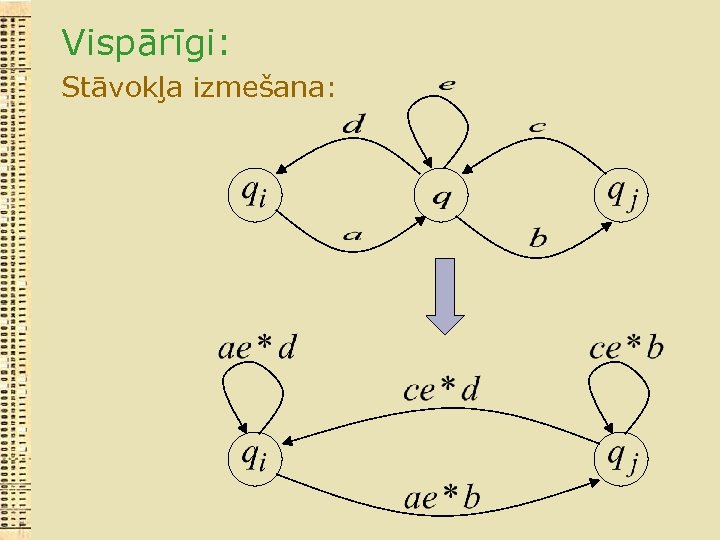 Vispārīgi: Stāvokļa izmešana:
Vispārīgi: Stāvokļa izmešana:
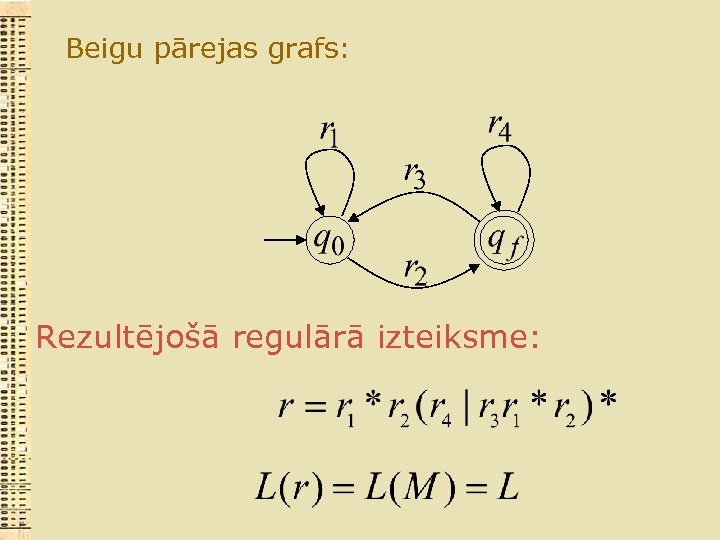 Beigu pārejas grafs: Rezultējošā regulārā izteiksme:
Beigu pārejas grafs: Rezultējošā regulārā izteiksme:
 Regulāras valodas apgrieztā valoda
Regulāras valodas apgrieztā valoda
 Teorēma: Regulāras valodas L apgrieztā valoda LR ir regulāra.
Teorēma: Regulāras valodas L apgrieztā valoda LR ir regulāra.
 Teorēma: Regulāras valodas L apgrieztā valoda LR ir regulāra. Pierādījuma ideja: Konstruēt GNA kas akceptē LR : apgriezt pretēji tās GNA pārejas, kas akceptē L
Teorēma: Regulāras valodas L apgrieztā valoda LR ir regulāra. Pierādījuma ideja: Konstruēt GNA kas akceptē LR : apgriezt pretēji tās GNA pārejas, kas akceptē L
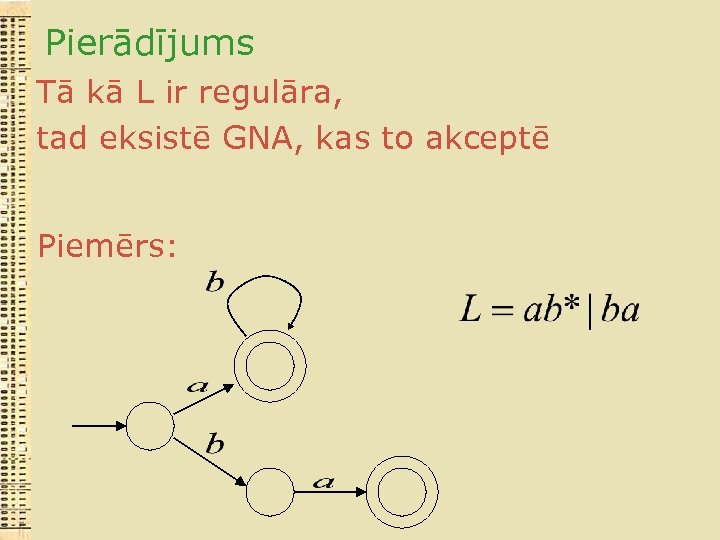 Pierādījums Tā kā L ir regulāra, tad eksistē GNA, kas to akceptē Piemērs:
Pierādījums Tā kā L ir regulāra, tad eksistē GNA, kas to akceptē Piemērs:
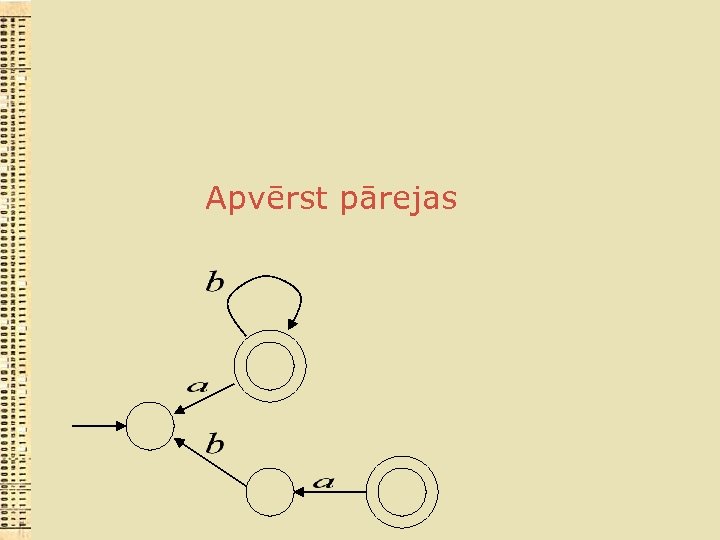 Apvērst pārejas
Apvērst pārejas
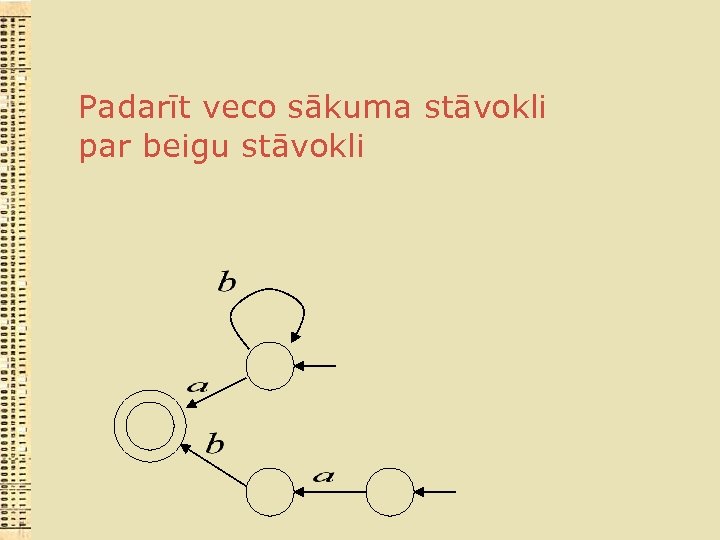 Padarīt veco sākuma stāvokli par beigu stāvokli
Padarīt veco sākuma stāvokli par beigu stāvokli
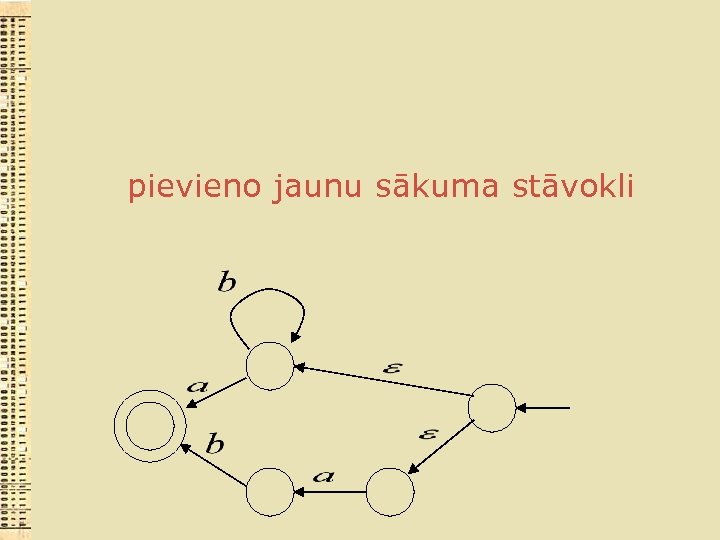 pievieno jaunu sākuma stāvokli
pievieno jaunu sākuma stāvokli
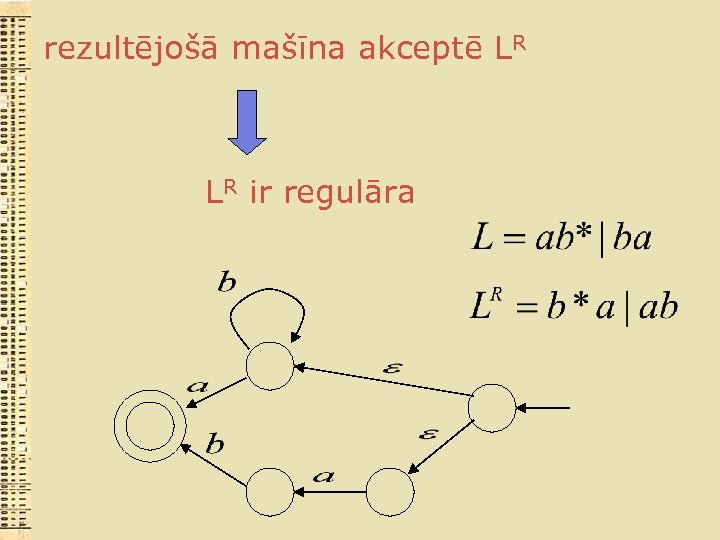 rezultējošā mašīna akceptē LR LR ir regulāra
rezultējošā mašīna akceptē LR LR ir regulāra
 Piemērs = { visas binārās virknes, kurās nav sastopamas divas secīgas nulles } Pašreiz Izveidot regulāru izteiksmi līdzīgai valodai, kur.
Piemērs = { visas binārās virknes, kurās nav sastopamas divas secīgas nulles } Pašreiz Izveidot regulāru izteiksmi līdzīgai valodai, kur.
 r = (01|1)*(1|01|0)
r = (01|1)*(1|01|0)


