Валентинов В. А. Эконометрика. Модуль 3. Оценка

Валентинов В. А. Эконометрика. Модуль 3. Оценка качества эконометрической модели Тема 9. Оценка тесноты связи Тема 10. Оценка качества подбора уравнения Тема 11. Проверка статистической значимости эконометрической модели Тема 12. Оценка значимости параметров эконометрической модели

Валентинов В. А. Эконометрика. 9. 1. Коэффициент корреляции 9. 2. Предпосылки коэффициента корреляции 9. 3. Свойства коэффициента корреляции 9. 4. Проверка статистической значимости коэффициента корреляции

Валентинов В. А. Эконометрика. 9. 1. Коэффициент корреляции Для определения степени связи между двумя случайными переменными Х и У вычисляется коэффициент корреляции по формуле: которая читается следующим образом: коэффициент корреляции между переменными Х и У равен частному от деления числителя на знаменатель, числитель равен сумме произведений отклонений Х и У от своих средних значений, знаменатель равен корню квадратному от произведения суммы квадратов отклонений Х и У от своих средних значений.

Валентинов В. А. Эконометрика. 9. 2. Предпосылки коэффициента корреляции Для корректного расчета коэффициента корреляции должны выполняться две предпосылки относительно переменных: 1 – переменные Х и У являются случайными величинами; 2 – переменные Х и У имеют нормальный закон распределения и являются однородными.

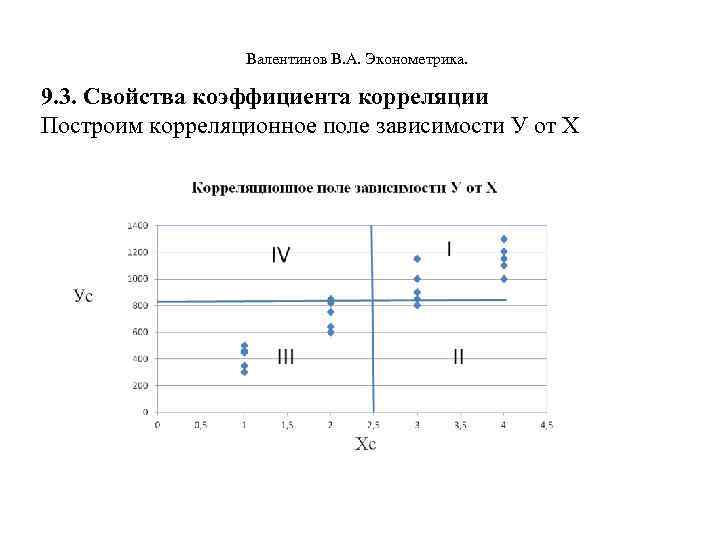Валентинов В. А. Эконометрика. 9. 3. Свойства коэффициента корреляции Построим корреляционное поле зависимости У от Х

Валентинов В. А. Эконометрика. Коэффициент корреляции обладает следующими свойствами: 1. Значения коэффициента корреляции r(x, y) могут находиться в интервале [-1, +1]. 2. Отрицательное значение r(x, y) означает, что при увеличении x наблюдается тенденция уменьшения y, положительное - при увеличении x наблюдается увеличение y. 3. Если между x и y существует функциональная линейная зависимость, то коэффициент корреляции принимает значения либо +1, либо -1. 4. Если коэффициент корреляции равен 0, то это означает, что между Х и У нет линейной зависимости, но может быть нелинейная зависимость. 5. Корреляционным полем называется график совместного распределения Х и У.

Валентинов В. А. Эконометрика. 9. 4. Проверка статистической значимости коэффициента корреляции Проверка статистической гипотезы о равенстве нулю истинного значения коэффициента корреляции необходима для того, чтобы определить наличие или отсутствие линейной тенденции взаимного изменения двух случайных величин. Этапы проверки статистической значимости коэффициента корреляции. Этап 1. Выдвигается нулевая гипотеза о том, значение коэффициента корреляции между Х и У для генеральной совокупности равен нулю Н 0: ρ(х, у) = 0 Нулевая гипотеза - это предположение о том, что между изучаемыми явлениями нет связи, численные значения характеристик объектов не отличаются между собой. Нулевые гипотезы проверяются с помощью статистических критериев. Уровень значимости (альфа) - означает вероятность совершить ошибку при отклонении нулевой гипотезы.

Валентинов В. А. Эконометрика. Этап 2. Вычисляется значение коэффициента корреляции Этап 3. вычисляется критическое значение коэффициента корреляции t(α=0, 05, m= n-2) – табличное значение критерия Стьюдента, на уровне значимости α=0, 05 и числе степеней свободы m= n-2. Этап 4. Сравнение r (x, y) c r кр Если r (x, y) > r кр , то нулевая гипотеза отвергается с вероятностью P=1 - α Если r (x, y) < r кр , то нулевая гипотеза принимается, но не указывается с какой вероятностью

Валентинов В. А. Эконометрика. Простота расчета и анализа коэффициента корреляции позволили широко использовать его в научных исследованиях. Если не соблюдаются предпосылки корреляционного анализа, расчет коэффициента корреляции является некорректным и полученные выводы могут быть ложными. Известны следующие виды ложной корреляции: - ложная корреляция временных рядов; - ложная корреляция Пирсона, определение связи между переменными, имеющими общую переменную; - ложная корреляция процентных чисел; - ложная корреляция стратификации, связь между двумя неоднородными переменными; - ложная корреляция для неслучайных переменных.

Валентинов В. А. Эконометрика. Тема 10. Оценка качества подбора уравнения 10. 1. Перечень показателей качества модели 10. 2. Ошибка модели 10. 3. Дисперсионный анализ регрессионной модели 10. 4. Коэффициент детерминации

Валентинов В. А. Эконометрика. 10. 1. Перечень показателей качества модели Качество подбора уравнения определяется с помощью следующих трех основных показателей качества модели: Е - ошибка модели, Е% - ошибка модели, вычисленная в процентах, R 2 - коэффициент детерминации.

Валентинов В. А. Эконометрика. 10. 2. Ошибка модели в абсолютных значениях вычисляется по формуле: где Е – ошибка модели, выраженная в единицах измерения У, n - объем выборки, k - количество всех коэффициентов модели, k = 2 для модели Ур = а 0+а 1*Х. Ошибка модели, выраженная в процентах, вычисляется по формуле: Принято считать, что если ошибка модели будет меньше 5%, то модель является достоверной.

Валентинов В. А. Эконометрика. 10. 3. Дисперсионный анализ регрессионной модели Дисперсия - свойство переменной Х, которая вычисляется делением вариации на ее число степеней свободы по формуле: где n - 1 - число степеней свободы вариации, n - объем выборки, - вариация признака Х. Дисперсионный анализ регрессионной модели состоит в разложении вариации зависимой переменной на вариации уравнения регрессии и остатков.

Валентинов В. А. Эконометрика. Дисперсионный анализ регрессионной модели состоит в разложении вариации зависимой переменной на вариации уравнения регрессии и остатков.

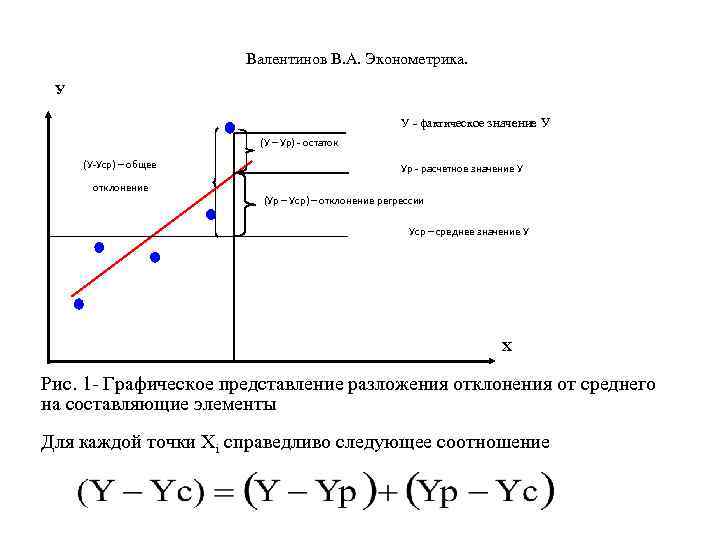Валентинов В. А. Эконометрика. У У - фактическое значение У (У – Ур) - остаток (У-Уср) – общее отклонение Ур - расчетное значение У (Ур – Уср) – отклонение регрессии Уср – среднее значение У Х Рис. 1 - Графическое представление разложения отклонения от среднего на составляющие элементы Для каждой точки Хi справедливо следующее соотношение

Валентинов В. А. Эконометрика. Для каждой точки Хi справедливо следующее соотношение Если левую и правую часть этого соотношения возвести в квадрат и просуммировать по всем измерениям, то получим основное вариационное соотношение

Валентинов В. А. Эконометрика. Вариационное соотношение записывают более коротко: Собщ = Сост + Срег, Собщ. - вариация общая, Сост. –вариация остатков, Срег – вариация регрессии, которое читается следующим образом: - вариация общая равна вариации остатков плюс вариация регрессии.

Валентинов В. А. Эконометрика. Составляющие элементы основного вариационного уравнения имеют соответствующие значения степеней свободы, которые связаны тождеством: (n – 1) = (n – k) + (k – 1), где n - 1 –число степеней свободы для вариации общей; n - k –число степеней свободы для вариации остатков; k - 1 –число степеней свободы для вариации регрессии; k – количество коэффициентов в уравнении регрессии. Дисперсии регрессионной модели вычисляются делением соответствующей вариации на свое значение числа степеней свободы по следующим формулам: S 2 общ = Собщ/(n-1) – дисперсия общая S 2 оcт = Cост/(n-k) - дисперсия остатков S 2 рег = Cрег/(k-1) – дисперсия регрессии

Валентинов В. А. Эконометрика. 10. 4. Коэффициент детерминации равен доли объясненной вариации от общего варьирования зависимой переменной: Множественный коэффициент корреляции.

Валентинов В. А. Эконометрика. Тема 11. Проверка статистической значимости эконометрической модели 11. 1. Критерии проверки значимости модели 11. 2. Коэффициент детерминации 11. 3. Критерий Фишера 11. 4. Проверка статистической значимости эконометрической модели

Валентинов В. А. Эконометрика. 11. 1. Критерии проверки значимости модели. Для проверки значимости модели используется коэффициент детерминации R 2 и критерий Фишера F. 11. 2. Коэффициент детерминации вычисляется по формуле: Принято считать, что если коэффициент детерминации больше 0, 7, то модель является хорошей.

Валентинов В. А. Эконометрика. 11. 3. Критерий Фишера Для более точного утверждения используется критерий Фишера. Фактическое значение критерия Фишера вычисляется по формуле

Валентинов В. А. Эконометрика. 11. 4. Проверка статистической значимости эконометрической модели Проверка достоверности модели производится с помощью статистического критерия Фишера по следующим шагам. Шаг 1. Выдвигается нулевая гипотеза Н 0: " Урас=Ус, между У и Х нет связи" Шаг 2. Вычисляется фактическое значение критерия Фишера

Валентинов В. А. Эконометрика. Шаг 3. Определяется критическое значение критерия Фишера на уровне значимости =0, 05. Fкр( = 0, 05, M 1 = k - 1, М 2 = n - k), где - уровень значимости М 1 - число степеней свободы для большей дисперсии регрессии, М 2 - число степеней свободы для меньшей дисперсии остатков, n – объем выборки, k – количество коэффициентов в уравнении регрессии. Шаг 4. Сравниваются фактические значения критерия Фишера с его критическим значением. Если F > Fкр( = 0, 05, М 1 = k-1, М 2 = n-k), то нулевая гипотеза отвергается с вероятностью 1 - и считается, что модель является достоверной. Если F < Fкр( = 0, 05, М 1 = k-1, М 2 = n-k), то нулевая гипотеза принимается и считается, что достоверность модели не доказана.

Валентинов В. А. Эконометрика. Тема 12. Оценка значимости параметров эконометрической модели 12. 1. Проверка статистической значимости параметров эконометрической модели 12. 2. Прогнозирование 12. 3. Доверительный интервал функции регрессии 12. 4. Эконометрический анализ регрессионной модели

Валентинов В. А. Эконометрика. 12. 1. Проверка статистической значимости параметров эконометрической модели Проверка значимости параметров модели У = α 0+α 1 Х + ɛ производится с помощью статистического критерия Стьюдента. Шаг 1. Выдвигаются нулевые гипотезы Н 0: α 0=0, которая читается следующим образом: нулевая гипотеза состоит в том, что параметр α 0 равен нулю. Н 0: α 1=0 Шаг 2. Вычисляются ошибки коэффициентов модели У = а 0+а 1 Х+е по формулам: Sа 0 - ошибка коэффициента а 0, Sa 1 - ошибка коэффициента а 1.

Валентинов В. А. Эконометрика. Шаг 3. Вычисляются фактические значения критерия Стьюдента ta 0 = a 0/Sa 0 , ta 1 = a 1/Sa 1. Критерий Стьюдента показывает во сколько раз коэффициент больше своей ошибки. Чем больше критерий Стьюдета, тем с большей вероятностью параметр будет отличаться от нулевого значений. Шаг 4. Определяется критическое значение критерия Стьюдента на уровне значимости = 0, 05. tкр( = 0, 05; М = n-k), где - уровень значимости, М - число степеней свободы для дисперсии остатков, n – объем выборки, k – количество коэффициентов в модели.

Валентинов В. А. Эконометрика. Шаг 5. Сравниваются фактическое значение критерия Стьюдента с его критическим значением. Если tа 1 > tкр( = 0, 05, М = n-k), то нулевая гипотеза отвергается с вероятностью 1 - и считается, что параметр α 1 достоверно отличается от нуля и влияние фактора Х является достоверным. Если tа 1 < tкр( = 0, 05, М = n-k), то нулевая гипотеза принимается и считается, что достоверность параметра α 1 статистически не доказана и влияние фактора Х статистически не доказано. Обычно, проверку значимости параметра α 0 не проводят, так как он не связан с влияющим фактором.

Валентинов В. А. Эконометрика. 12. 2. Прогнозирование Методологической основой прогнозирования являются инерционные свойства экономической системы. В настоящем присутствуют элементы прошлого и зачатки будущего Точечный прогноз- это среднее значение прогнозной переменной, которое вычисляется по формуле Упр = а 0+а 1*Хож, где Упр - прогнозное значение зависимой переменной на ожидаемый период, Хож - численное значение объясняемой переменной на ожидаемый период. Интервальный прогноз - это интервал, в котором с определенной вероятностью может находиться фактическое значение прогнозной величины.

Валентинов В. А. Эконометрика. С вероятность 1 - можно утверждать, что индивидуальное значение прогноза будет находиться в интервале от Упр - Ош. пр. и. до Упр + Ош. пр. и. , где Ош. пр. и. - ошибка прогноза для индивидуальных значений зависимой переменной, t - критерий Стьюдента на уровне значимости и числе степеней свободы м, (альфа) - уровень значимости, n - объем выборки, k - количество коэффициентов в уравнении регрессии, Е - ошибка прогноза, Хi - текущее значение объясняемой переменной, Хс - среднее значение объясняемой переменной, Хож. - ожидаемое значение объясняемой переменной.

Валентинов В. А. Эконометрика. Ошибка прогноза для индивидуальных значений обладает следующими свойствами: Свойство 1. Чем дальше находится Хож от Хс, тем больше прогнозный доверительный интервал. Свойство 2. Чем больше ошибка модели Е , тем больше прогнозный доверительный интервал. Свойство 3. Чем меньше , тем больше t , тем больше прогнозный доверительный интервал. Свойство 4. Чем больше n , тем меньше прогнозный доверительный интервал, Свойство 5. Чем больше вариация Х , тем меньше прогнозный доверительный интервал. Вывод. Для того, чтобы уменьшить прогнозный доверительный интервал для индивидуальных значений зависимой переменной необходимо улучшить спецификацию модели, увеличить объем выборки, увеличить дисперсию объясняемой переменной.

Валентинов В. А. Эконометрика. С вероятность 1 - можно утверждать, что прогнозное значение математического ожидания зависимой переменной будет находиться в интервале от Упр - Ош. пр. м. до Упр + Ош. пр. м. , где Ош. пр. м. - ошибка прогноза для математического ожидания зависимой переменной.

Валентинов В. А. Эконометрика. 12. 3. Доверительный интервал функции регрессии. Существуют два вида интервальных прогнозов уравнения регрессии для: индивидуальных значений и математических ожиданий. С вероятность 1 - можно утверждать, что уравнение регрессии для индивидуальных значений будет находиться в интервале от Ур - Ош. рег. и. до Ур + Ош. рег. и. , где Ош. рег. и. - ошибка регрессии для индивидуальных значений зависимой переменной, Урi = а 0 +а 1*Хi - расчетные значения зависимой переменной.

Валентинов В. А. Эконометрика. С вероятность 1 - можно утверждать, что уравнение регрессии для индивидуальных значений будет находиться в интервале от Ниж. д. и. рег. = Ур - Ош. рег. и. до Вер. д. и. рег. = Ур + Ош. рег. и. , где Ош. рег. и. - ошибка регрессии для индивидуальных значений зависимой переменной, Ниж. д. и. рег. - нижний доверительный интервал уравнения регрессии Вер. д. и. рег. – верхний доверительный интервал уравнения регрессии

Валентинов В. А. Эконометрика. 12. 4. Эконометрический анализ регрессионной модели. Эконометрический анализ проводится в следующей последовательности: 1. Приводится условие задачи и база данных всех переменных, которые участвовали в построении модели. 2. Строится график зависимости между переменными. 3. Приводятся все характеристики модели. 4. Проверяется достоверность модели и ее коэффициентов. 5. Приводится точечный и интервальный прогноз на ожидаемый период. 6. Приводится графическое представление всех результатов расчетов с указанием фактических и расчетных значений зависимой переменной, 95% доверительных интервалов для уравнения регрессии, точечный прогноз и 95% прогнозный доверительный интервал для зависимой переменной. 7. Делаются выводы и предложения по результатам эконометрического анализа.

Валентинов В. А. Эконометрика. Спасибо за внимание Москва Март 2013 г.