Валентинов В. А.

Валентинов В. А. Эконометрика. ФГОС. ООП 080100. 62 - Экономика. Бакалавры 2 курс, 3 поколение. Модуль 1. Линейная модель множественной регрессии Тема 1. Спецификация эконометрической модели. Тема 2. Отбор факторов, включаемых в модель множественной регрессии. Тема 3. Фиктивные переменные. Тема 4. Линейное уравнение множественной регрессии

Валентинов В. А. Эконометрика. Тема 1. Спецификация эконометрической модели. 1. 1. Определение эконометрики 1. 2. Пример решения эконометрической задачи 1. 3. Спецификация эконометрической модели 1. 1. Определение эконометрики. Термин «эконометрика» состоит из двух частей: «эконо» — от «экономика» и «метрика» — от «измерение» , которые означают экономические измерения. Эконометрика – наука, которая использует методы математической статистики в экономических исследованиях. В настоящее время эконометрическим обществом принято следующее определение эконометрики. Эконометрика — наука, изучающая количественные и качественные экономические взаимосвязи с помощью математических и статистических методов и моделей. Объектом эконометрики являются экономические процессы, происходящие в экономической системе общества. Предметом эконометрики является количественная оценка взаимосвязи между случайными переменными экономических объектов, проверяя теоретические модели реальных экономических процессов для получения прогнозов деятельности экономических систем. Целью эконометрики является оценка точечных и интервальных прогнозов деятельности всех объектов экономической системы на основании расчетов по данным выборочной совокупности.

Валентинов В. А. Эконометрика. Задачами эконометрики являются: -разработка методов расчета коэффициентов моделей при соблюдении и нарушении предпосылок метода наименьших квадратов, - проверка достоверности модели и ее коэффициентов; -получение точечного и интервального прогноза экономического процесса,

Валентинов В. А. Эконометрика. 1. 2. Пример решения эконометрической задачи Задача 1. Имеются численные значения двух показателей: количество продавцов и розничного товарооборота по четырем выборочным однородным филиалам одной фирмы, представленные в таблице 1. Таблица 1 - База данных по четырем филиалам одной фирмы i Хi Уi 1 1 4 2 3 6 3 2 7 4 4 10 5 5 ? Где: i - номер филиала фирмы, Х - количество продавцов (чел. ), У - величина розничного товарооборота (тыс. руб. ). Необходимо получить прогноз розничного товарооборота для открывающегося пятого филиала фирмы, в котором ожидается количество продавцов равного пяти.

Валентинов В. А. Эконометрика. Решение задачи. Нам неизвестна зависимость У от Х, поэтому выдвигаем следующие гипотезы: Предполагаем, что зависимость У от Х можно представить в виде классической нормальной линейной модели парной регрессии. Приводим спецификацию данной модели: Уi = + Xi+ i, i = 1, 2, … , n; У – случайная величина (стохастическая); Х – неслучайная (детерминированная) величина; - нормально распределенная случайная величина со средним ср=0 и дисперсией равной 2 , где , - неизвестные параметры; - неизвестное возмущение; 2 - неизвестная дисперсия возмущения ; М – знак математического ожидания; n – объем выборки. Напомним некоторые основные понятия регрессионного анализа с помощью графического представления данных, см. рис 1.

Валентинов В. А. Эконометрика. Рис. 1 - Графический анализ данных

Валентинов В. А. Эконометрика. Проведем аппроксимационную линию так, чтобы разница между фактическими и расчетными значениями розничного товарооборота (остатки) были минимальными. Если говорить более строго, то необходимо так провести линию, чтобы сумма квадратов остатков была минимальной. Для оценки параметров , и возмущения , будем использовать коэффициенты а 0 , а 1 и остатки е следующего линейного парного уравнения регрессии, вычисленных по выборочной совокупности объемом n = 5: Уi= а 0+а 1*Хi+еi = Урi+еi, где: Уi - фактические значения розничного товарооборота; i – порядковый номер измерения; а 0 – свободный коэффициент линейного уравнения регрессии равный значению Ур при Х = 0; а 1 - коэффициент пропорциональности между У и Х, равного приросту Ур при изменении Х на единицу. В нашем примере коэффициент а 1 означает среднею производительность труда продавцов; Урi = а 0 +а 1*Хi - расчетные значения розничного товарооборота; е i = У i - Ур i - остатки модели, учитывающие влияние факторов, не включенные в модель.

Валентинов В. А. Эконометрика. Визуальный анализ графика зависимости У от Х позволяет приблизительно вычислить коэффициенты парной регрессии. а 0=2, 5 а 1 =1, 7 Ур =2, 5+1, 7 * Х Если в уравнение регрессии подставить ожидаемое значение Хож = 5, то можно получить прогнозное значение Упр. Упр =2, 5+1, 7*Хож = 2, 5+1, 7*5 =11 тыс. руб. Вывод. Для выборочной совокупности фирм зависимость розничного товарооборота от количества продавцов можно представить в виде парного линейного уравнения регрессии: Уi =2, 5+1, 7 * Хi+ei. Средняя производительность труда продавцов составляет 1, 7 тыс. руб. на одного продавца. Если в новой фирме ожидается 5 продавцов, то среднее прогнозное значение товарооборота будет равно 11 тыс. руб. Однако, коэффициенты а 0, а 1, определенные по выборки равной пяти будут отличаться от истинных параметров , , которые можно определить по всей бесконечной генеральной совокупности. Для более точного определения коэффициентов уравнения регрессии используется метод наименьших квадратов.

Валентинов В. А. Эконометрика. 1. 3. Спецификация эконометрической модели Слово «спецификация » (от лат. species – род, вид, разновидность и facio – делаю) термин, обозначающий набор требований и параметров, которым удовлетворяет некоторая сущность. Спецификацией эконометрической модели называется отбор факторов, включаемых в модель, и выбор математической функции для У на основании имеющейся или предполагаемой связи между переменными.

Валентинов В. А. Эконометрика. Спецификация эконометрической модели является составной частью этапов эконометрического моделирования. Можно выделить следующие этапы эконометрического моделирования. 1 - определение цели исследования; 2 - определение факторов, влияющие на зависимый показатель; 3 - проверка связи между переменными; 4 - составление перечня факторов, которые могут быть включены в модель; 5 -спецификация эконометрической модели; 6 - отбор факторов, включаемых в модель множественной регрессии; 7 - оценка параметров линейных уравнений регрессии; 8 - оценка качества подбора уравнения; 9 - проверка статистической значимости модели и ее параметров; 10 - получение точечного и интервального прогноза; 11 - выводы и предложения.

Валентинов В. А. Эконометрика. Спецификация эконометрической модели считается произведенной, если выполнены следующие требования: 1) определены цели исследования; 2) определены факторы, влияющие на зависимый показатель; 3) проведена проверка связи между переменными; 4) имеется перечень факторов, которые могут быть включены в модель; 5) выбран вид модели, учитывающей влияние выбранных факторов; 6)- проверено условие: объем выборки должен быть в 6 -7 раз больше количества факторов, включенных в модель; 7) проверено условие возможности расчета коэффициентов методом наименьших квадратов; 8) изучена возможность четкой экономической интерпретации коэффициентов модели и проведения прогнозирования.

Валентинов В. А. Эконометрика. Тема 2. Отбор факторов, включаемых в модель множественной регрессии. 2. 1. Правила включения факторов в модель 2. 2. Мультиколлинеарность 2. 3. Методы корреляционной матрицы и корреляционных плеяд для включения факторов в модель 2. 4. Метод шагового включения

Валентинов В. А. Эконометрика. 2. 1. Правила включения факторов в модель Для включения факторов в модель множественной регрессии можно использовать следующие правила: 1 – количество факторов в модели должно быть в 6 -7 раз меньше объема выборки численных значений по каждому фактору ; 2 – в модель необходимо включать все основные факторы и несколько второстепенных; 3 - в модель можно включать факторы, которые сильно связаны с зависимой переменной и слабо связаны между собой

Валентинов В. А. Эконометрика. Лекция 2. Отбор факторов, включаемых в модель множественной регрессии 2. 2. Мультиколлинеарность - это свойство связи факторов между собой. Мультиколлинеарность является свойством экономической системой. Причиной мультиколлинеарности является свойство экономической системы, в которой все переменные экономических объектов должны быть взаимосвязаны между собой. Иначе экономическая система не будет существовать. Мультиколлинеарность может быть существенной и несущественной. Мультиколлинеарность является существенной , если существует хотя бы одна пара переменных, включенных в модель, между которыми имеется существенная связь, определяемая по коэффициенту корреляции.

Валентинов В. А. Эконометрика. Последствия мультиколлинеарности заключаются в том, что при построении многофакторной модели, в которой факторы мультиколлинеарны, возникают следующие проблемы в определении коэффициентов и качества модели. а). Нельзя определить коэффициенты модели по формуле так как нельзя найти обратную матрицу в которой матрица факторов Х содержит зависимые переменные. б). Если мультиколлинеарность несущественная, то удается определить коэффициенты модели, однако ошибки коэффициентов становятся очень большими, так как ошибки коэффициентов модели зависят от диагональных элементов матрицы в). Если мультиколлинеарность является существенной, то коэффициенты модели теряют экономический смысл. г). При включении в модель нового мультиколлинеарного фактора предыдущие значения коэффициентов изменяются и их ошибки возрастают, достоверность модели снижается. Это свойство факторов может быть средством обнаружения мультиколлинеарности.

Валентинов В. А. Эконометрика. 2. 3. Методы корреляционной матрицы и корреляционных плеяд для включения факторов в модель Существуют следующие эффективные методы включения факторов в модель: - метод корреляционной матрицы; - метод корреляционных плеяд для парных и частных коэффициентов корреляции; -шаговый метод включения

Валентинов В. А. Эконометрика. Метод корреляционной матрицы Для реализации метода корреляционной матрицы между всеми переменными рассчитываются парные коэффициенты корреляции по формуле: где r(X, У) - фактический коэффициент корреляции между переменными Х и У; Далее заполняют корреляционную матрицу, представленную в таблице 2. 1.

Валентинов В. А. Эконометрика. Таблица 2. 1 – Матрица парных коэффициентов корреляции Х 1 Х 2 Х 3 У Х 1 Х 2 r(Х 2, Х 1) 1 Х 3 r (Х 3, Х 1) r(Х 3, Х 2) 1 У r(У, Х 1) r(У, Х 2) r(У, Х 3) 1 Примечание. В таблице 2. 1 показана только нижняя часть таблицы, так как верхняя часть равна нижней, например, r(Х 2, Х 1)= r(Х 1, Х 2).

Валентинов В. А. Эконометрика. Достоверность коэффициента корреляции проверяется методом сравнения фактического коэффициента с критическим. Если фактический коэффициент корреляции по модулю больше критического, то линейная связь между двумя переменными является достоверной. В противном случае линейная связь между двумя переменными статистически является недоказанной. Критическое значение коэффициента корреляции rкр. вычисляется по формуле: где t ( = 0, 05, n - 2 ) - табличное значение критерия Стьюдента, - уровень значимости, равный вероятности совершить ошибку при отклонении нулевой гипотезы, n - объем выборки. Далее проводится анализ парных коэффициентов корреляции на достоверность связи между собой. Определяются факторы для включении в модель в соответствии с установленными правилами.

Валентинов В. А. Эконометрика. Метод корреляционных плеяд выполняется в следующей последовательности: 1 - определяются зависимая переменная У и факторы Х, которые влияют на У, 2 - собирается база данных по переменным и заполняется таблица исходных значений всех переменных, 3 - между всеми переменными рассчитываются парные коэффициенты корреляции; 4 - коэффициенты корреляции оформляются в виде матрицы парных коэффициентов корреляции , при условии, что имеется зависимая переменная У и три фактора Х 1, Х 2, Х 3; 5 - на круговой диаграмме линиями соединятся те факторы и зависимая переменная, между которыми существует достоверный коэффициент корреляции. 6 – решение о включении факторов в модель делается на основании основных правил их включения.

Валентинов В. А. Эконометрика. Метод корреляционных плеяд можно использовать для частных коэффициентов корреляции. Частный коэффициент корреляции учитывает связь между двумя переменными, при условии, что все остальные факторы не изменяются. Частные коэффициенты корреляции рассчитываются по формуле: где частный коэффициент корреляции определяется между факторами Хi и XJ при условии, что остальные факторы не изменяются, С - элементы обратной матрицы, определенной от матрицы парных коэффициентов корреляции. Коэффициент корреляции можно получить с помощью функции Ехсе 1 – статистические, КОРРЕЛ Обратную матрицу можно получить с помощью функции Ехсе 1 – математические, МОБР.

Валентинов В. А. Эконометрика. Лекция 2. Отбор факторов, включаемых в модель множественной регрессии 2. 4. Метод шагового включения Модели, построенные шаговым методом и методом корреляционных плеяд для частных коэффициентов корреляции, часто совпадают между собой. Шаговый метод является самым лучшим метод построения модели при наличии мультиколлинеарности между переменными. Различают шаговую регрессию: включения, исключения, включения и исключения. Практическое распространение получила шаговая регрессия включения. Метод включения состоит в том, что в модель включаются факторы по одному в определенной последовательности. Построение модели заканчивается, если модель перестает удовлетворять определенным условиям. Шаговый метод включения построения модели заключается в том, что на каждом шаге в модель вводится по одному фактору и проверяется достоверность модели по критическому критерию Фишера, численное значение которого вводится пользователем. Если после ввода в регрессионное уравнение нового фактора критерий Фишера стал меньше критического, то построение модели заканчивается.

Валентинов В. А. Эконометрика. Лекция 2. Отбор факторов, включаемых в модель множественной регрессии Алгоритм шаговой регрессии очень сложный. Но его можно реализовать достаточно просто по следующей упрощенной схеме. На первом шаге в модель вводится тот фактор, который имеет наибольший коэффициент корреляции с зависимой переменной. На втором шаге и последующих шагах в модель включается фактор, который имеет наибольший коэффициент корреляции с остатками модели. После каждого включения фактора в модель рассчитываются ее характеристики и проверяются на достоверность. Если после включения в модель фактора модель стала недостоверной, то на этом построение модели заканчивают.

Валентинов В. А. Эконометрика. Тема 3. Фиктивные переменные. 3. 1. Определение фиктивной переменной 3. 2. Определение модели с переменной структурой 3. 3. Область использования фиктивной переменной 3. 4. Пример использования фиктивной переменной

Валентинов В. А. Эконометрика. При построении регрессионной модели может возникнуть ситуация, когда необходимо включить в уравнение помимо количественных переменные, отражающие некоторые качественные переменные. Фиктивная переменная – качественная переменная, отражающая некоторые атрибутивные признаки (пол, образование, регион и т. п. ). Чаще всего применяются бинарные фиктивные переменные, принимающие два значения, 0 и 1, в зависимости от определенного условия. Например, в результате опроса группы людей 0 может означать, что опрашиваемый - мужчина, а 1 - женщина.

Валентинов В. А. Эконометрика. Лекция 3. Фиктивные переменные 3. 2. Определение модели с переменной структурой Модели называются моделями с переменной структурой, если в состав объясняемых переменных входят, как количественные, так и фиктивные факторы.

Валентинов В. А. Эконометрика. 3. 3. Область использования фиктивной переменной Фиктивные переменные отражают неоднородность исследуемой статистической совокупности и используются для более качественного моделирования зависимостей в таких неоднородных объектах наблюдения. В практике эконометрики часто используют фиктивные переменные для следующих целей: 1 - учета влияния атрибутивных факторов: пол, образование, стиль управления, удовлетворенность потребителей, семейное положение, климатические условия, принадлежность к определенному региону, сезон и т. д. ; 2 - объяснения сильно выделяющихся значений зависимой переменной (выбросы); 3 – учета влияния факторов, которые не вошли в модель; 4 - повышения точности прогноза. Имеется одно ограничение использования фиктивных переменных – если сумма нескольких фиктивных переменных, для каждых измерений, имеет одно и тоже значение, то фиктивные переменные и переменная, учитывающая свободный коэффициент, являются мультиколлинеарными и рассчитать коэффициенты модели не удается.

Валентинов В. А. Эконометрика. Лекция 3. Фиктивные переменные 3. 4. Пример использования фиктивной переменной Пусть необходимо определить влияние некоторой качественной переменной z, принимающей два возможных значения. Обозначим эти возможные значения A и B для определенности. Тогда такой переменной можно поставить в соответствие следующую фиктивную переменную Пусть исходная модель имеет вид Если добавить переменную d в модель, то получим

Валентинов В. А. Эконометрика. Тема 4. Линейное уравнение множественной регрессии 4. 1. Общий вид уравнения множественной регрессии 4. 2. Виды множественной линейной регрессии 4. 3. Экономическая интерпретация коэффициентов линейного уравнения 4. 4. Примеры экономической интерпретации коэффициентов линейного уравнения

Валентинов В. А. Эконометрика. 4. 1. Общий вид уравнения множественной регрессии Линейная модель множественной регрессии для генеральной совокупности имеет вид: Уi = α 0 + α 1 Х 1 i + α 2 Х 2 i +. . . + αm Хmi + εi, где У- зависимая переменная (результативный признак); Хji - независимые переменные (факторы), j – порядковый номер фактора; i –. номер измерения; αj - параметры регрессии, которые обозначаются греческими буквами; εi – случайное возмущение, которое отражает влияние тех факторов, которые не вошли в модель, ошибок наблюдений или измерений.

Валентинов В. А. Эконометрика. Параметры модели для генеральной совокупности мы будем писать греческими, а их оценки для выборочных совокупностей латинскими буквами и называть их будем коэффициентами. Уравнение множественной регрессии содержит значения неизвестных параметров α 0, α 1, α 2, . . . , αm. Эти величины оцениваются на основе выборочных наблюдений, поэтому полученные значения, обозначаемые латинскими буквами и называемые коэффициентами, не являются истинными, а представляют собой лишь статистические оценки параметров регрессии.

Валентинов В. А. Эконометрика. 4. 2. Виды множественной линейной регрессии Существуют два вида множественной линейной регрессии: аддитивная и мультипликативная. Аддитивная множественная линейная регрессия для выборочной совокупности, в которой вместо истинных значений параметров подставлены их оценки, имеет вид: Yi = а 0 + а 1 Х 1 i + а 2 Х 2 i +. . . + аm Хmi + еi, где а 0, а 1, а 2 – называют коэффициентами и обозначают латинскими буквами. Широкое применение получил еще один вид многофакторной модели, в которой коэффициенты соединены мультипликативно (умножением). Приводим мультипликативную многофакторную степенную модель: Уi = а 0 Х 1 iа 1 Х 2 i а 2. . . Хmi аmеi, которая называется производственной моделью и носит название модели Кобба – Дугласа.

Валентинов В. А. Эконометрика. 4. 3. Экономическая интерпретация коэффициентов линейного уравнения Проведем для выборочной совокупности анализ аддитивной двухфакторной линейной модели: Уi = а 0 + а 1 Х 1 i + а 2 Х 2 i + еi = Урi+еi. У – зависимая переменная; Ур – расчетные значения У; Х 1, Х 2 – независимые переменные, факторы; ei – остатки модели; а 0 – свободный коэффициент (свободный член уравнения), который равен численному значению Ур, при условии, что численные значения факторов Х 1 и Х 2 равны нулю; а 1, а 2 – коэффициенты, которые являются оценками параметров α 1 и α 2. Коэффициент а 1 означает, насколько изменится значение Ур при изменении Х 1 на единицу, при условии, что численное значение Х 2 не изменится. Коэффициент а 2 означает, насколько изменится значение Ур при изменении Х 2 на единицу при условии, что численное значение Х 1 не изменится.

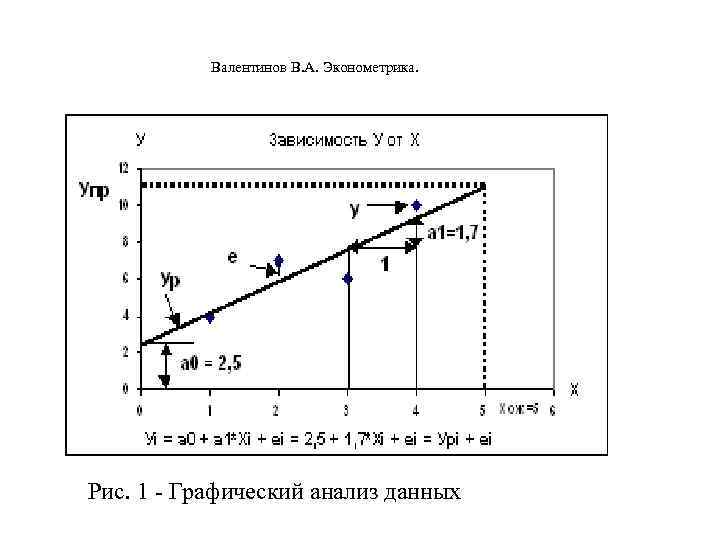
Валентинов В. А. Эконометрика. 4. 4. Примеры экономической интерпретации коэффициентов линейного уравнения Пример 1. Получено уравнение Ур = а 0+а 1 Х 1, где У – товарооборот, Х 1 – численность продавцов, а 1 означает, насколько увеличится товарооборот при изменении числа продавцов на единицу или среднюю производительность работы продавцов. Пример 2. Получено уравнение Ур = а 0+а 1 Х 1, где У – вес продукции, Х 1 – длина продукции, метр, а 1 означает вес одного метра продукции или насколько увеличится вес продукции при изменении длины продукции на единицу. Пример 3. Получено уравнение Ур = а 0+а 1 Х 1, где У – товарооборот за месяц, Х 1 –товарооборачиваемость продукции за месяц, разы, а 1 означает размер одного цикла товарооборота или насколько увеличится товарооборот при изменении товарооборачиваемости на единицу.