Лекции спец.главы математики.pptx
- Количество слайдов: 49

* В ряде случаев более удобным способом решения уравнений является способ итераций (повторений). Для применения этого способа исходное уравнение ƒ(c)=0 нужно представить в форме х = φ(х) (2. 7) Это всегда можно сделать, и при том многими способами. Например, уравнение х3 - 2 х - 5 = 0 можно заменить следующими равносильными уравнениями: Пусть каким-либо способом выделен интервал [а, b], в котором находится значение корня уравнения, и х0 – любая точка этого интервала. Будем считать х0 нулевым приближением. Подставим х0 в правую часть уравнения (2. 7) и получим первое приближение x 1 = φ(x 0). Значение х1, снова подставим в уравнение (2. 7), получим второе приближение х2 = φ(х1). Аналогичным способом находим х3 = φ(х3), х4 = φ(х4) и т. д. Этот процесс можно продолжать неограниченно, получая последовательность чисел х0, х1, х2, . . . , хn , … Если эта последовательность имеет предел limn→∞ хn= х*, то х* является корнем уравнения (2. 7). В самом деле предполагая, что φ(х) – непрерывная функция, получим

Однако может случится, что последовательность х0, х1, х2, . . . , хn , … не имеет предела и даже расходится, тогда этот способ не применим. Представляет большой интерес выяснить условия, при которых итерационный процесс сходится. Эти условия вытекают из следующей теоремы. Теорема. Пусть интервал [а, b] является интервалом, в котором находится только один корень уравнения х = φ(х) и во всех точках этого интервала производная φ’(х) удовлетворяет неравенству. |φ(х)| ≤ М < 1 (2. 8) Если при этом выполняется условие а ≤ φ(х) ≤ b, то итерационный процесс сходится, причем за нулевое приближение х0 можно взять любую точку интервала [а, b]. Пример. Дано уравнение х3 + 12 х – 2 = 0. Найти один положительный корень. Выделим интервал, в котором содержится один корень. Результаты представим в табл. 2. х f(x) 0 2 1 11 0, 5 4, 125 0, 2 0, 408 0, 1 -0, 8 Из приведенной таблицы следует, что уравнение имеет значение корня, заключенное между 0, 1 и 0, 2. Для уточнения корня применим способ итераций. Представим заданное уравнение в виде (2. 7), что удобно для применения этого способа, а именно: (2. 8)

Примем за начальное приближение х0 = 0, 16 и будем вычислять последовательные приближения, подставляя их в (2. 8) предыдущие приближенные значения корня. В результате получим: х = 0, 1600, 0 х1 = 0, 16628 0, 1663, х2 = 0, 1663 Видим, что приближения xt и х2 совпадают. При дальнейшем вычислении будем получать одно и то же число. Поэтому на втором приближении процесс закончим. При возрастании номера члены последовательности приближаются к истинному значению корня , т. е. полученное приближение является приближенным значением с недостатком. Причем х2 = 0, 1663 есть искомое приближенное значение корня с четырьмя десятичными знаками. Поясним геометрически способ итераций. Построим на плоскости х. Оу графики функций у = х и у = φ(х). Каждый действительный корень х* уравнения (2. 7) является абсциссой точки пересечения М кривой у = φ(х) с прямой у = х – рис. 2. 3 Отправляясь от некоторой точки А 0[х0, φ(х0)], строим ломаную линию А 0 В 1 А 1 В 2 А 2. . . ( «лестница» ), звенья которой попеременно параллельны оси Ох и Оу. Вершины А 0 А 1 А 2, . . . лежат на кривой у = φ(х), а вершины В 1, В 2 на прямой y = х. Общие абсциссы точек A 1 и B 1, А 2 и В 2, и т. д. , очевидно, представляют собой последовательные приближения x 1, x 2 , . . . корня х*.
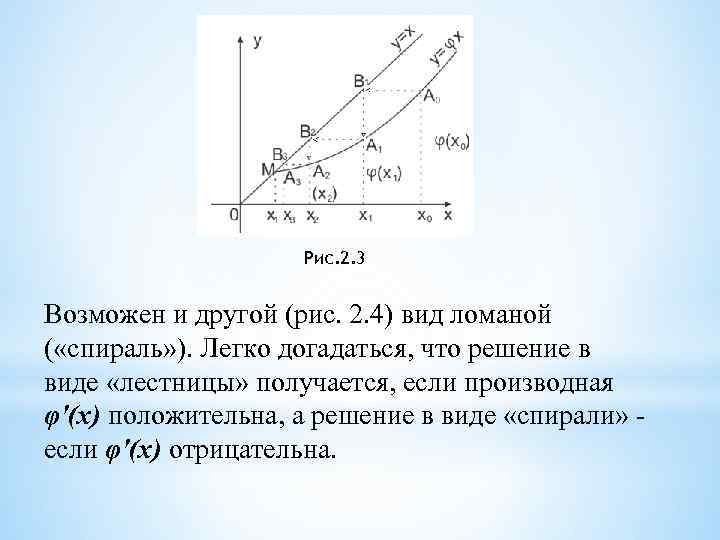
Рис. 2. 3 Возможен и другой (рис. 2. 4) вид ломаной ( «спираль» ). Легко догадаться, что решение в виде «лестницы» получается, если производная φ'(х) положительна, а решение в виде «спирали» - если φ'(х) отрицательна.
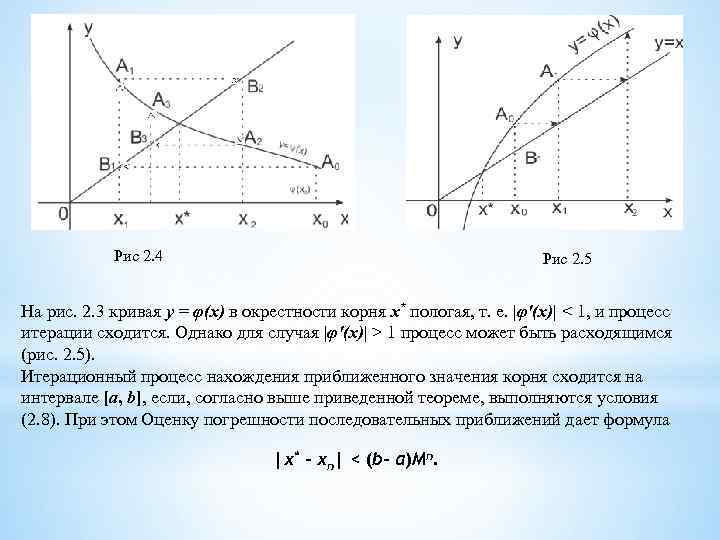
Рис 2. 4 Рис 2. 5 На рис. 2. 3 кривая у = φ(х) в окрестности корня х* пологая, т. е. |φ'(х)| < 1, и процесс итерации сходится. Однако для случая |φ'(х)| > 1 процесс может быть расходящимся (рис. 2. 5). Итерационный процесс нахождения приближенного значения корня сходится на интервале [а, b], если, согласно выше приведенной теореме, выполняются условия (2. 8). При этом Оценку погрешности последовательных приближений дает формула |х* - хп| < (b- а)Мп.

2. 4. Решение систем линейных уравнений способом Гаусса Способ Гаусса является одним из наиболее распространенных способов решения систем линейных уравнений. Если точно выполнить все необходимые действия, то мы получим точное решение системы. В этом смысле способ Гаусса называют точным. Практически, поскольку арифметические действия приходится выполнять с округлением, точного решения получить не удается. В основе способа Гаусса лежит идея последовательного исключения неизвестных. Вычислительные схемы реализации этого способа могут быть различны. Мы рассмотрим одну из них – схему единственного деления. Для удобства изложения ограничимся рассмотрением примера конкретной системы четвертого порядка. Те же приемы используются и в случае большего числа уравнений в системе: (2. 9) Предположим, что коэффициент , называемый ведущим элементом первой строки, не равен нулю. Разделив первое из уравнений (2. 6) на , получим: (2. 10) где

Исключим х1, вычитая из каждого уравнения системы (2. 9), начиная со второго, уравнение (2. 10), умноженное на коэффициент при x 1, в соответствующем уравнении. В результате получим (2. 11) где i = 2, 3, 4; j = 2, 3, 4, 5. Допустим, что ведущим является элемент второй строки Тогда, разделив на него члены первого из уравнения (2. 11), получим уравнение ≠ 0. (2. 12) где Исключив с помощью уравнения (2. 12) неизвестную величину х2 из двух последних уравнений (2. 11), приходим к уравнениям вида (2. 13) где i = 3, 4; j = 3, 4, 5.

0 Если ведущим является элемент третьей строки , то, поделив на него члены первого ≠ из уравнений (2. 13) и вычтя найденное уравнение, умноженное на из второго уравнения, получим (2. 14) (2. 15) где ≠ 0 Наконец, если элемент , то, разделив на него уравнение (2. 15), приведем его к виду (2. 16) где = Итак, мы получим систему с треугольной матрицей, эквивалентной системе (2. 9) (2. 17)

Эта система получена путем объединения уравнений (2. 10), (2. 12), (2. 14) и (2. 16). Процесс приведения системы (2. 9) к треугольному виду (2. 17) называется прямым ходом, а нахождение неизвестных из системы (2. 17) – обратным ходом. Решение системы уравнений по способу Гаусса удобно производить, занося все вычисления в табл. 2. 3 Таблица 2. 3
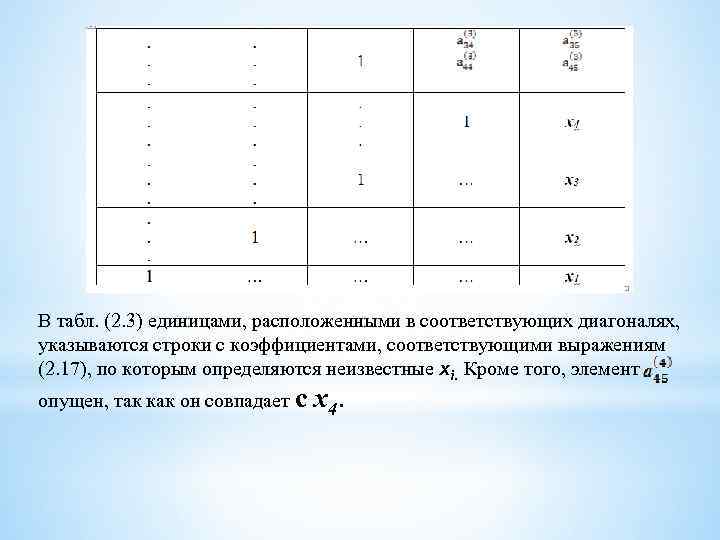
В табл. (2. 3) единицами, расположенными в соответствующих диагоналях, указываются строки с коэффициентами, соответствующими выражениям (2. 17), по которым определяются неизвестные хi. Кроме того, элемент опущен, так как он совпадает с х4.

* При большем числе неизвестных линейной системы схема Гаусса, с помощью которой осуществляют методически точные решения, становится весьма сложной. В этих случаях для нахождения корней системы удобнее применять приближенные численные способы. Одним из таких способов является способ итераций. Пусть дана линейная система (2. 18) Представим систему (2. 18) в матричном виде, введя соответствующие матрицы А= (2. 19) Предполагая, что диагональные коэффициенты не равны 0 (аij ≠ 0, i = 1, 2 , …, n), разрешим первое уравнение (2. 18) относительно x 1, второе - относительно х2 и т. д. Тогда получим эквивалентную систему (2. 20)

α= систему (2. 20) можно записать в матричной форме: х = β + αх (2. 21) Эту систему можно решать методом последовательных приближений. За нулевое приближение можно принять столбец свободных членов х(0) = β. Далее находим первое приближение в виде матрицы-столбца х(1) = β + αх(0), затем второе приближение х(2) = β + αх(1) и т. д. Любое (к+1)-е приближение вычисляют по формуле х(k+1) = β + αх(k), k = 0, 1, 2 , … (2. 22) Если последовательность приближений x(0), x(1), …, x(k), … имеет предел этот предел является решением системы (2. 20). , то

Процесс итераций хорошо сходится, если элементы матрицы α малы по абсолютной величине. Иными словами, для успешного применения способа итераций модули диагональных коэффициентов системы (2. 18) должны быть велики по сравнению с модулями диагональных коэффициентов этой системы (свободные члены роли не играют). Пример. Решить систему способом итераций В данной системе диагональные коэффициенты значительно преобладают над остальными коэффициентами при неизвестных. Приведем эту систему к виду (2. 20): (2. 23) За нулевые приближения корней системы (2. 20), примем свободные члены, т. е.

Подставляя эти значения в правые части уравнений (2. 23), получим первые приближения корней: Далее, подставляя первые приближения в систему (2. 23), получим вторые приближения корней После новой подстановки будем иметь третьи приближения корней: На этом процесс нахождения корней можно закончить. Проведя округление до второго десятичного знака, получим корни с абсолютной погрешностью менее 0, 005;

2. 6. Приближенное решение систем нелинейных уравнений методом Ньютона Запишем нелинейную систему уравнений в общем виде (2. 24) Эту систему можно записать короче в матричном виде, рассматривая совокупность аргументов как n-мерный вектор: а совокупность функций f 1, f 2 , …, fn – тоже как n-мерный вектор:

Тогда будем иметь f(х) = 0. (2. 25) Для решения системы (2. 24) будем пользоваться методом последовательных приближений. Предположим, что найдено р-е приближение х(р) = ( ) одного из корней х = (х1, х2, …, хn) векторного уравнения (2. 25). Тогда точный корень уравнения можно представить в виде х = х(р) + ε(р) = 0, (2. 26) где ε(р) = ( ) – погрешность корня. Подставляя выражение (2. 26) в уравнение (2. 25), будем иметь f (х(р) + ε(р)) = 0. (2. 27)

Предполагая, что функция f(х) непрерывна, и дифференцируема, разложим левую часть уравнения (2. 27) по степеням малого вектора ε(р), ограничиваясь линейными членами f(х(р) + ε(р)) = f(х(р))+ f’(х(р)) ε(р) = 0, (2. 28) где f’(x) есть матрица Якоби системы функций f 1, f 2, …, fn относительно переменных х1, х2, …, хn, т. е. Учитывая эту матрицу, формулу (2. 28) можно записать в виде f(х(р)) + W(х(р))ε(p) = 0. Отсюда, предполагая, что матрица W(х(р)) неособенная (ее определитель не равен 0), получим W(х(р)) ε(p) = - f(х(р))

По аналогии с методом касательных, где (n+1) – е приближение выражается через формулу (2. 4), (р+1) – е приближение в нашем случае можно записать в виде х(р+1) = x(p) – W-1(x(p))f(x(p)), p = 0, 1, 2, … (2. 29) За нулевое приближение х(0) можно взять грубые значения искомого корня. Пример. Методом Ньютона найти приближенное решение системы уравнений За начальное приближение примем следующие значения неизвестных: х0 = у0 = z 0 = 0, 5.

Составим матрицу Якоби: Найдем определитель W(x(0)): Находим обратную матрицу:

По формуле (2. 29) получаем первое приближение: Таким образом, имеем первое приближение Зная первое приближение х(1), вычисляем второе приближение х(2): Матрица Якоби для данного случая будем иметь вид

Отсюда находим определитель Далее находим обратную матрицу Используя формулу (2. 29), находим второе приближение:

Таким образом, второе приближение имеет вид Аналогично находим дальнейшие приближения. 3. Интерполирование 3. 1 Общие сведения об интерполировании Первоначально под интерполированием понималось отыскание значений функции, соответствующих промежуточным значениям аргумента, которых нет в таблице. При этом интерполяцию можно было бы определить как «искусство чтения между строк» . В настоящее время задача интерполяции понимается шире. В известном смысле можно сказать, что задача интерполирования обратна задаче табулирования функции. При табулировании по аналитическому выражению функции находят таблицу ее значений, а при интерполировании, наоборот, по таблице значений функции строят ее аналитическое выражение. Поясним, что следует под этим понимать.
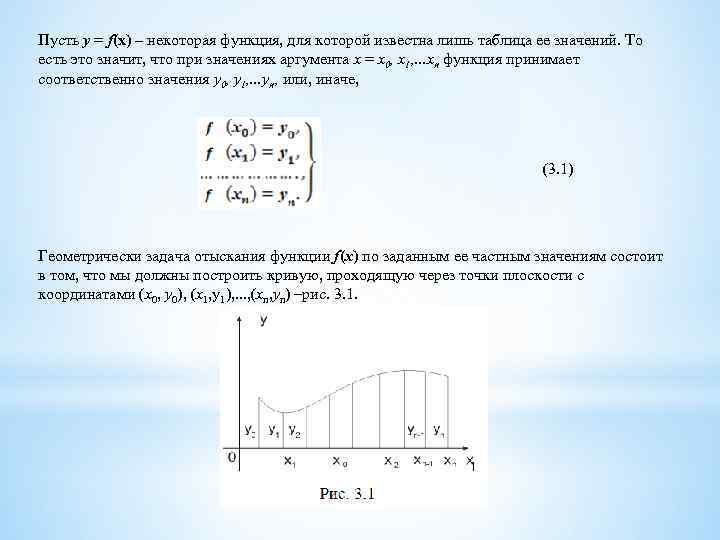
Пусть у = f(x) – некоторая функция, для которой известна лишь таблица ее значений. То есть это значит, что при значениях аргумента х = x 0, x 1, . . . xn функция принимает соответственно значения у0, у1, . . . уn, или, иначе, (3. 1) Геометрически задача отыскания функции f(x) по заданным ее частным значениям состоит в том, что мы должны построить кривую, проходящую через точки плоскости с координатами (х0, у0), (х1, у1), . . . , (хn, уn) –рис. 3. 1.

Очевидно, что через данные точки можно провести бесчисленное множество различных кривых. Поэтому задача отыскания функции f(x) по конечному числу заданных ее значений слишком неопределенна. Мы будем обозначать в дальнейшем такую функцию F(х), и их может быть сколько угодно. Предположим теперь, что функция F(x) не произвольная, а удовлетворяет некоторым дополнительным требованиям, чтобы задача приобретала более определенный характер. Чаще всего требуют, чтобы функция F(x) была многочленом степени, на единицу меньшей, чем число известных значений. Таким образом, мы приходим к следующей формулировке задачи: для данных значений х = х0, х1, . . . , хп и у = у0, у1 , . . . , уп найти многочлен у = F(x) степени n, удовлетворяющий условиям (3. 2) Иначе говоря, необходимо отыскать многочлен, принимающий в заданных точках заданные значения. Такую задачу называют задачей параболической интерполяции. Точки х0, х1 , . . . , хп называют узлами интерполяции. Многочлен F(x), удовлетворяющий условиям (3. 2), называется интерполяционным, а формулы для его построения – интерполяционными формулами.

Основная идея применения интерполяционных формул состоит в том, что функция у = f(x), для которой известна лишь таблица значений (3. 1), заменяется интерполяционным многочленом, который рассматривается как приближенное аналитическое выражение для функции f(x). При этом возникают вопросы о степени точности такого приближения и об оценках погрешности, появляющиеся при замене f(x) на F(x). 3. 2 Интерполяционная формула Лагранжа Для получения интерполяционной формулы Лагранжа мы будем исходить из понятия параболического интерполирования. Рассмотрим функцию f(x), для которой заданы значения уi = f(xi), i = 0, 1, 2, …, n, причем все хi уiизвестны. Требуется определить многочлен у = F(x) степени n, для которою F(xi) = f(xi). Искомый многочлен можно записать в виде (3. 3) Чтобы отыскать неизвестные коэффициенты a 0, a 1, . . . , an, используя приведенные выше условия, можно написать систему из (n + 1) уравнений с (n +1) неизвестными. Эта система будет иметь следующий вид: (3. 4)

Вместо того, чтобы решать систему уравнений (3. 4), можно поступить иначе: непосредственно построить многочлен F(x), удовлетворяющий всем поставленным условиям. Найдем прежде всего выражение для многочлена, принимающего в точке х = х0 значение у0 = 1, а в точках х = х1, х = х2 , …, х = хn – значения у1 = у2 =. . . = уп = 0. Можно проверить, что такой многочлен будет иметь следующий вид: Действительно, значения х = х1, х = х2 , …, х = хn являются корнями этого многочлена, а при х = х0 числитель равен знаменателю. Теперь построим многочлен у = F 0(x), принимающий в точке х = x 0 значение y 0 и обращающийся в нуль для значений x = xi (i = 0, 1, 2, . . . , n). Учитывая предыдущее построение, нетрудно заметить, что многочлен F 0(x) должен иметь вид После этих предварительных построений можно перейти к отысканию многочлена F(x), принимающего в точках x = xi (i = 0, 1, 2, . . . , n) заданные значения F(xi) = уi. . Для этого определим при фиксированном индексе j (0 ≤ j ≤ n) многочлен Fj(x), принимающий в точке x = хj значение Fj(xj) = yj = F(xj), а во всех остальных точках x = xi (i = 0, 1, 2, . . . , n, i ≠ j) значения F 2(xi)=0. Очевидно, это будет многочлен

Искомый многочлен будет равен сумме так как в каждой точке хj только одно из слагаемых принимает нужное значение yj, а все остальные слагаемые обращаются в нуль. Итак, искомый многочлен найден. Подставляя в сумму вместо Fj(x) их выражения, получим (3. 5) В развернутом виде выражение (3. 5) имеет вид (3. 6)

Полученная формула (3. 6) называется интерполяционной формулой Лагранжа. Рассмотрим примеры. Положим п = 1. В этом случае мы имеем две точки х0 и х1, и формула Лагранжа дает уравнение прямой. Обозначив абсциссы этих точек х0=а и х1=b, получим интерполяционный многочлен в виде Теперь положим n = 2. Тогда мы получим уравнение параболы, проходящей через три точки. Абсциссы этих точек обозначим х0 = а, х1 = b, х2 = с. Тогда искомое уравнение будет иметь вид 3. 3. Конечные разности До сих пор мы не делали никаких предположений о значениях аргумента. Предположим, что рассматриваемые значения аргумента являются равноотстоящими. Такое предположение обычно имеет место при интерполировании функций, заданных в виде таблиц с постоянным шагом, т. е. x 1 = x 0 + h, х2 = х0 + 2 h, . . . , xm = х0 + mh, где h - это шаг таблицы. Построение интерполяционной формулы в этом случае упростится.

Но прежде чем перейти к рассмотрению данного вопроса, необходимо познакомиться с понятием конечных разностей. Пусть значения функции заданы в точках x 0, xn= x 0 + h, …, xn = x 0 + nh. Составим разности значений функции: y 1 – y 0 = f(x 0 + h) – f(x 0) = Δy 0 = Δf(x 0), y 2 – y 1 = f(x 0 + 2 h) – f(x 0 + h) = Δy 1 = Δf(x 0 + h), ………………………… yn – yn-1 = f(x 0 + nh) – f(x 0 + (n – 1)h) = Δyn-1 = Δf(x 0 + (n – 1)h). Эти значения называют первыми разностями функции, или разностями первого порядка. По ним мы можем составить разности второго порядка или вторые разности: Δ 2 y 0 = Δy 1 – Δy 0, Δ 2 y 1 = Δy 2 – Δy 1, …, Δ 2 ym = Δym+1 – Δym. Разности любого порядка k будут иметь вид Δkym = Δk-1 ym+1 – Δk-1 ym (3. 7) Эти последовательные разности обычно располагают в форме таблиц. Применяются две формы таблиц последовательных разностей – диагональные и горизонтальные. В диагональных таблицах (табл. 3. 1) разности в каждом столбце записываются между соответствующими значениями уменьшаемого и вычитаемого.

Так как разности обычно бывают невелики, то их записывают без нулей впереди. Равенства: (3. 7) определяют разности различных порядков последовательно. Интерес представляют выражения для конечных последовательностей, установленные непосредственно через значения функций. Установим их. Так как Δy 0 = y 1 – y 0; Δy 1 = y 2 – y 1, то Δ 2 y 0 = Δy 1 – Δy 0 = (у2 – у1) – (у1 – у0). Поэтому Δ 2 y 0 = y 2 – 2 y 1 + y 0.

Точно так же найдем третью разность, выраженную через значения функций: Нетрудно показать, что для любого значения k разность будет иметь (3. 8) Формула (3. 8) имеет место и для разности Δkym. Достаточно ко всем номерам значений функций прибавить индекс m. 3. 4. Интерполяционные формулы Ньютона При получении интерполяционных формул Ньютона, которые используются для тех же целей, что и формула Лагранжа, сделаем дополнительное предположение, что рассматриваются равноотстоящие значения аргумента. Итак, пусть значения функции у = f(x) заданы для равноотстоящих значений x 0, x 1 = x 0 + h, …, xn = x 0 + nh. Этим значениям аргументов будут соответствовать значения функции: у0 = f(x 0), у1 = f(x 1), …, yn = f(xn).

Запишем искомый многочлен в виде Для определения коэффициентов a 0, a 1, . . . , аn положим в (3. 9) х = х0. Тогда у0 = F(x 0)=а 0. Далее, полагая x=x 1, получим у1= F(x 1) = a 0 + а 1 h, откуда Продолжая вычисления коэффициентов, положим х = х2. Тогда Исходя из (3. 8), получаем y 2 – 2 y 1 + y 0 = Δ 2 y 0. Поэтому

Точно так же получим Аналогичные дальнейшие вычисления позволяют записать общую формулу для любого коэффициента аk: Подставим найденные выражения коэффициентов в формулу (3. 9), получим Полученная формула и называется первой интерполяционной формулой Ньютона. Для практического использования формулу Ньютона (3. 10) обычно записывают в преобразованном виде. Для этого введем обозначение

Выразим через t множители, входящие в формулу (3. 10): Подставив полученные выражения в формулу (3. 10), окончательно получаем Выражение (3. 11) представляет окончательный вид первой интерполяционной формулы Ньютона. Пример. Приняв шаг h =0, 05, построить на отрезке [3, 5; 3, 7] интерполяционный полином Ньютона для функции y = ex, заданной табл. 3. 3.

Решение. Составим таблицу разностей Заметим, что в столбцах разностей, следуя обычной практике, мы не отделяем запятой десятичные разряды, которые ясны из столбца значений функций. Так как разности третьего порядка практически постоянны, то в формуле (3. 11) полагаем n = 3. Приняв х0 = 3, 50 и у0 = 33, 115, будем иметь:

Первая интерполяционная формула Ньютона неудобна для интерполирования функции в конце таблицы, где число значений разностей мало. В этом случае применяется вторая интерполяционная формула Ньютона, которую мы сейчас и рассмотрим. Напишем искомый интерполяционный многочлен в виде Как и ранее, коэффициенты а 0, а 1, … аn определяются из условия F(xi) = yi. Положим в (3. 12) х = хn. Тогда a 0 = yn. Точно так же, полагая x = xn-1, получим yn-1 = yn +a 1(xn-1 - xn), а так как xn-1 – xn = - h, то Далее, полагая в (3. 12) x = xn-2 и, заменяя найденные коэффициенты а 0, а 1 их значениями, получаем

Числитель последнего выражения можно представить так: yn – yn-1 – (yn-1 - yn-2) = Δ yn-1 - Δ yn-2 = Δ 2 yn-2. Продолжая аналогичные вычисления, получим общую формулу для коэффициентов После подстановки в (3. 12) всех значений коэффициентов эта формула примет вид Это и есть вторая интерполяционная формула Ньютона. Для удобства применения ее, как и первую, преобразуют, введя обозначения

Выразим теперь через t множители в формуле (3. 13): Произведя такую замену, окончательно получим:
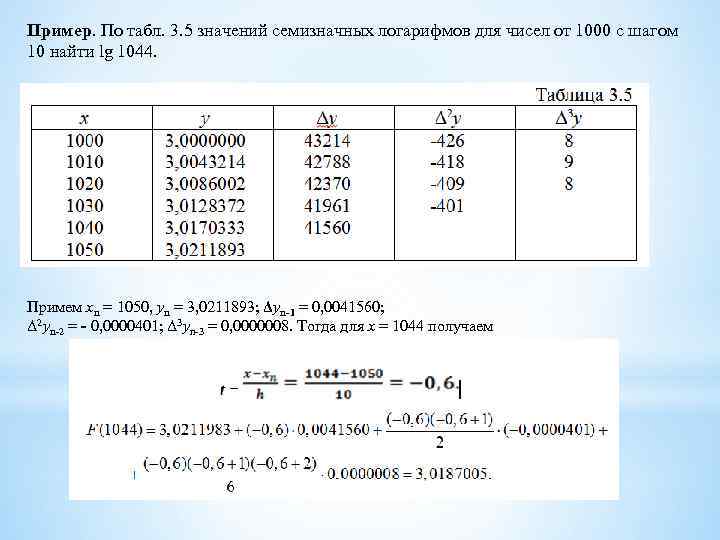
Пример. По табл. 3. 5 значений семизначных логарифмов для чисел от 1000 с шагом 10 найти lg 1044. Примем xn = 1050, yn = 3, 0211893; Δyn-1 = 0, 0041560; Δ 2 yn-2 = - 0, 0000401; Δ 3 yn-3 = 0, 0000008. Тогда для x = 1044 получаем

Как первая, так и вторая интерполяционные формул Ньютона могут быть использованы для экстраполирования функций, т. е. для нахождения значений функций для значений аргументов х, лежащих вне пределов таблицы. Если значение x < x 0 и значение x близко к x 0, то выгодно применять первую интерполяционную формулу Ньютона, причем Если же x > x 0 и x близко к хп, то удобнее пользоваться второй интерполяционной формулой Ньютона, причем Таким образом, первая интерполяционная формула Ньютона обычно используется для интерполирования вперед и экстраполирования назад, а вторая интерполяционная формула Ньютона, наоборот, – используется для интерполирования назад и экстраполирования вперед. Пример. Имея табл. 3. 6 значений и разностей, у = sin х: в пределах от х = 15° до х = 55° с шагом h = 5°, найти sin 14° и sin 56°.

Здесь следует выполнить экстраполирование назад, поэтому применим первую интерполяционную формулу Ньютона и подчеркнутые одной чертой конечные разности:

3. 5. Обратная интерполяция и многочлены Чебышева До сих пор мы рассматривали лишь задачи отыскания значений функций, соответствующих данным значениям аргумента, отсутствующим в таблице. Между тем нередко приходится сталкиваться с задачами иного характера: по таблице функции отыскать значение аргумента x, которому соответствует данное значение функции, отсутствующее в таблице. Так поставленную задачу называют задачей обратной интерполяции. Задачу обратной интерполяции легко обратить, считая значения функции значениями аргумента. Однако так как разности функции отличаются не на постоянную величину, то обратная интерполяция приводит к необходимости интерполировать в таблице, значения аргумента в которой не являются равноотстоящими. По этой причине для обратной интерполяции применяется обычно интерполяционная формула Лагранжа или другие методы.

Пример. Функция у = f(x) задана табл. 3. 7, определить, какому значению х соответствует значение функции у = 2, 4142. Чтобы не менять обозначений в интерполяционных формулах, поменяем местами х и у. Тогда будем иметь функцию у = φ(x), значения которой заданы табл. 3. 8 и для которой требуется найти φ(2, 4142). При этом значения х уже не будут равноотстоящими.

Пользуясь формулой Лагранжа (3. 6), в которой следует положить x= = 2, 4142, найдем

Вычислив значения дробей, получим у = 0, 88138. Таким образом, φ(2, 4142) = 0, 88138, т. е. значение х, при которой заданная табл. 3. 7 функция f(x), принимает значение 2, 4142, равно 0, 88138. При интерполяции на отрезке [а, b] возникает вопрос, как выбрать узлы х0, х1, . . . , хn интерполяционного многочлена, чтобы максимальная погрешность интерполяции функции f(x) была минимальной. Эта задача в общем случае является сложной, и ее удается решить только для частной функции f(x). При этом рассматриваются многочлены Чебышева Тп(х) на стандартном отрезке [-1, 1], n ≥ 0. Они задаются формулой Тn(х) = cos (n · arcos x) В частности, при n = 0, 1 имеем Т 0(х) = cos(0 · arcos x) = 1; (3. 15)

Полагая T 0(x) = 1, T 1(х) = х на всей оси и распространяя рекуррентную формулу (3. 16) на всю ось x последовательно по формуле (3. 16) находим Доказано, что узлы, минимизирующие оценку погрешности интерполяции на отрезке [-1, 1] многочленом Тn+1(х), определяются соотношением 3. 6. Оценка погрешностей интерполяционных формул Лагранжа и Ньютона После построения интерполяционного многочлена возникает вопрос, насколько близко построенный многочлен приближается к функции f(x) в точках, отличных от узлов. В этом случае рассматривают остаточный член |Rn(x)|=|f(x) – Ln(x)|. В данном случае Ln(x) – многочлен Лагранжа.

Анализ показывает, что абсолютная погрешность интерполяционной формулы Лагранжа имеет вид Отсюда очевидно, что максимальное значение М 3 будет, если из отрезка [100, 144] выбрать x = 100, т. е.

На основании формулы (3. 17) получаем Для первой интерполяционной формулы Ньютона (3. 11) остаточный член Rn(х) представляется в виде где ξ – некоторое промежуточное значение между узлами интерполирования х0, х1, х2, …, хn и рассматриваемой точкой х; h = xi+1 – xi;

Аналогично получается остаточный член для второй интерполяционной формулы Ньютона (3. 13), только здесь Пример. Оценить погрешность приближения функции f(x) = sin x интерполяционным полиномом пятой степени F 5(x), совпадающим с данной функцией при значениях x = 00, 50, 100, 150, 200, 250. Решение. Здесь f (6)(x) = - sin x, поэтому | f (6)(x) | ≤ 1. На основании формулы (3. 18) имеем
Лекции спец.главы математики.pptx