В Поле равномерно заряженной сферической поверхности Пусть сфера

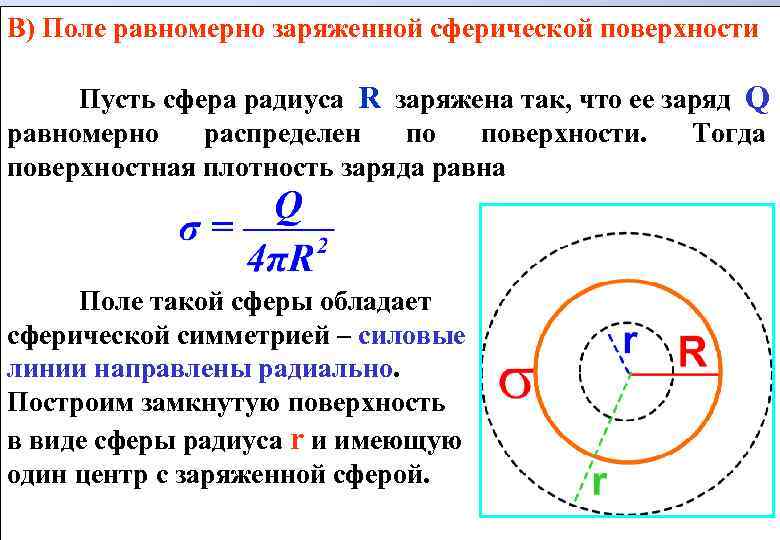В) Поле равномерно заряженной сферической поверхности Пусть сфера радиуса R заряжена так, что ее заряд Q равномерно распределен по поверхности. Тогда поверхностная плотность заряда равна Поле такой сферы обладает сферической симметрией – силовые линии направлены радиально. Построим замкнутую поверхность в виде сферы радиуса r и имеющую один центр с заряженной сферой.

Если r < R , то внутри замкнутой поверхности нет зарядов, поэтому поле равно нулю E = 0, а значит и внутри заряженной сферы радиуса R поле тоже равно нулю. Если , то внутрь замкнутой поверхности попадает весь заряд сферы, поэтому по теореме Остроградского-Гаусса Откуда (1. 16) Таким образом, вне сферы поле тождественно полю точечного заряда той же величины и расположенного в центре сферы. Непосредственно на сфере напряженность поля равна.

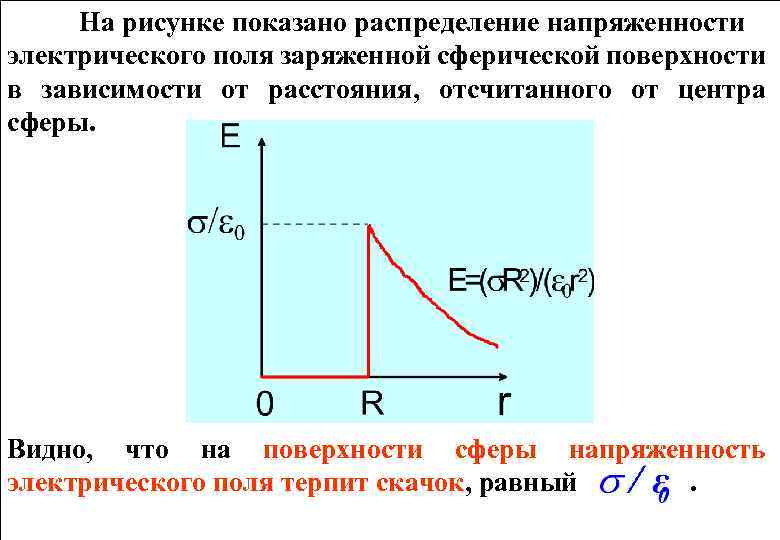На рисунке показано распределение напряженности электрического поля заряженной сферической поверхности в зависимости от расстояния, отсчитанного от центра сферы. Видно, что на поверхности сферы напряженность электрического поля терпит скачок, равный.

Г) Поле объемно заряженного шара Рассмотрим шар радиуса R заряженный с постоянной объемной плотностью. Его электрическое поле тоже обладает сферической симметрией. Снова построим замкнутую поверхность в виде концентрической сферы радиуса r. Если весь заряд шара Q, равный , то внутри этой поверхности будет По теореме Остроградского-Гаусса, как и ранее, получаем Откуда напряженность поля вне шара равна (1. 17)

Если r < R , то внутри замкнутой поверхности находится заряд, равный поэтому по теореме Остроградского-Гаусса Следовательно, напряженность поля внутри шара равна (1. 18)

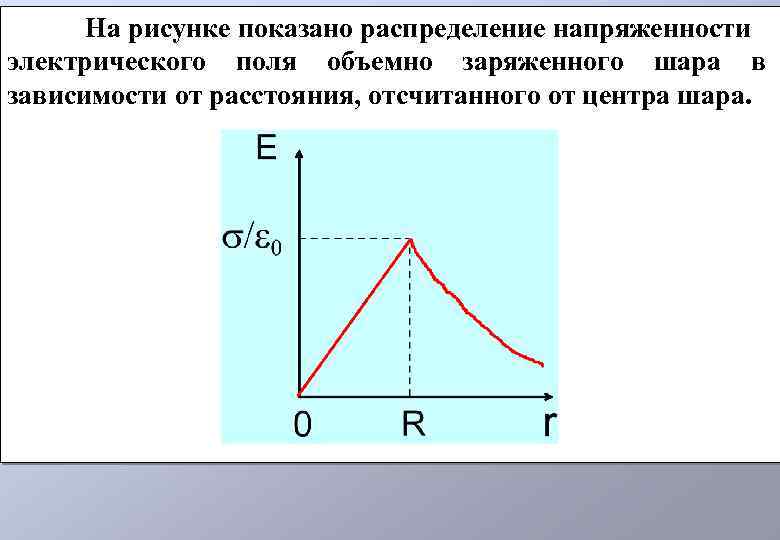На рисунке показано распределение напряженности электрического поля объемно заряженного шара в зависимости от расстояния, отсчитанного от центра шара.

Д) Поле бесконечного заряженного цилиндра Рассмотрим цилиндр радиуса R заряженный равномерно с линейной плотностью. Из симметрии цилиндра как фигуры следует, что напряженность поля в любой точке должна быть направлена по прямой, перпендикулярной оси цилиндра. Выберем замкнутую поверхность в виде коаксиального цилиндра радиуса r и длиной L. Поток через его торцы равен нулю, так как силовые линии их не пересекают. Пусть r > R тогда поток через боковую поверхность цилиндра равен

Здесь Q – заряд внутри выбранной замкнутой поверхности (пунктирный цилиндр). Отсюда получаем напряженность поля вне цилиндра (1. 19) где - линейная плотность заряда. Введем поверхностную плотность заряда согласно где S – площадь боковой поверхности. Выражая через и подставляя в (1. 19), получаем другое выражение для напряженности поля вне цилиндра (1. 20)

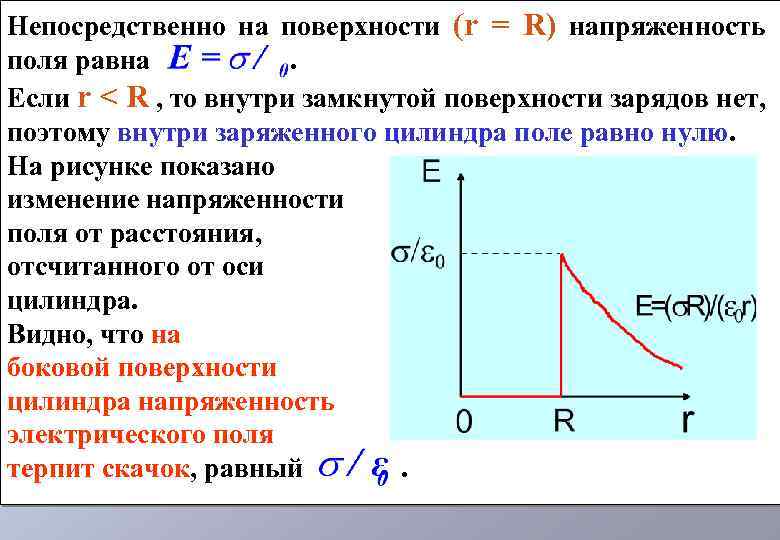Непосредственно на поверхности (r = R) напряженность поля равна. Если r < R , то внутри замкнутой поверхности зарядов нет, поэтому внутри заряженного цилиндра поле равно нулю. На рисунке показано изменение напряженности поля от расстояния, отсчитанного от оси цилиндра. Видно, что на боковой поверхности цилиндра напряженность электрического поля терпит скачок, равный.

9. Понятие о дивергенции векторной функции Ранее было получено выражение для потока вектора , через замкнутую поверхность S Преобразуем поверхностный интеграл в объемный, считая что электрическое поле неоднородно. Для этого выберем поверхность S в виде небольшого прямоугольного параллелепипеда с ребрами, параллельными декартовым осям, и центром (точка Р), имеющем радиус-вектор. В этом случае поверхностный интеграл сводится к 6 - ти интегралам по 6 - ти граням.

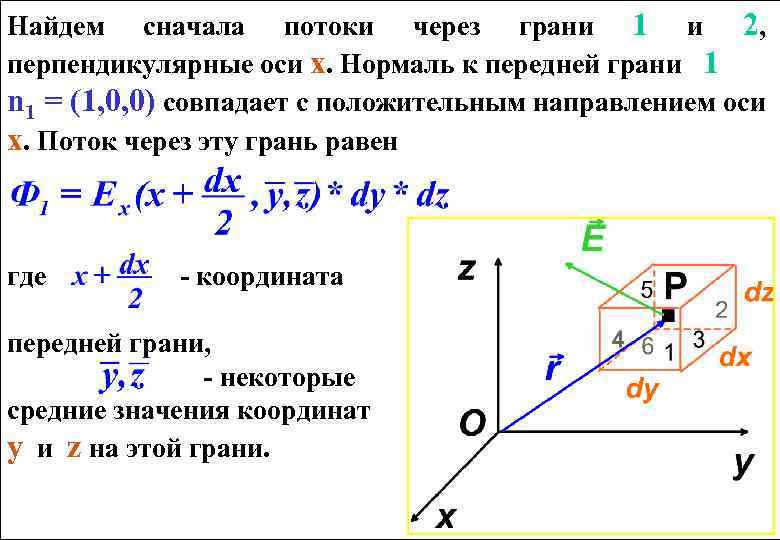Найдем сначала потоки через грани 1 и 2, перпендикулярные оси х. Нормаль к передней грани 1 n 1 = (1, 0, 0) совпадает с положительным направлением оси х. Поток через эту грань равен где - координата передней грани, - некоторые средние значения координат у и z на этой грани.

Нормаль к задней грани 2 n 2 = (-1, 0, 0) направлена противоположно оси х, поэтому поток через нее равен Сумма этих двух потоков равна

где d. V = dx*dy*dz - объем параллелепипеда. Аналогично находится сумма потоков через грани 3 и 4, перпендикулярные оси y и грани 5 и 6, перпендикулярные оси z Суммарный поток через все 6 граней равен (1. 21)

Скалярная величина, равная сумме частных производных (1. 22) называется дивергенцией вектора напряженности электрического поля (divergentia – лат. ). Из формул (1. 21) и (1. 22) следует, что (1. 23) С другой стороны, поток вектора охватывающую объем d. V, равен через поверхность S,

поэтому можем записать (1. 24) Значит, дивергенция вектора в точке с радиусвектором равна потоку этого вектора через поверхность, ограничивающую единичный объем, находящийся вблизи данной точки.

Для малого объема d. V поток через охватывающую его поверхность S можно записать как поэтому формулу (1. 24) можно представить в виде (1. 25) Таким образом, дивергенция пропорциональна плотности электрических зарядов в заданной точке пространства.

Введем векторный дифференциальный оператор градиента (оператор набла) оператор - (1. 26) Подействуем этим оператором на вектор напряженности электрического поля подобно скалярному произведению двух векторов Сравнивая с (1. 22), находим (1. 27)

Поэтому (1. 28) Это равенство выражает собой теорему Остроградского. Гаусса в дифференциальной форме.

Если объем V, охватываемый поверхностью S не мал, то поток вектора через поверхность находится из формулы (1. 22) путем интегрирования по объему V Учитывая, что с другой стороны получаем (1. 29) Это и есть искомая формула перехода от объемного интеграла к поверхностному и наоборот. Она справедлива не только для напряженности электрического поля , но и для любого векторного поля.

10. Потенциал. Работа сил электрического поля. Рассмотрим электрическое поле точечного заряда q. Если в это поле поместить другой заряд q´, то на него будет действовать кулоновская сила где - единичный вектор, направленный вдоль радиусвектора , соединяющего заряд q с зарядом q´. Кулоновская сила центральная, поэтому она консервативная и следовательно работа, совершаемая этой силой при перемещении заряда q´ в поле заряда q не зависит от пути.

Пусть 1 и 2 начальная и конечная точки, в которых находился заряд q´. Работа кулоновской силы на пути между этими точками равна (1. 30) где r 1 и r 2 – расстояния между зарядами q и q´ в начале и конце движения заряда q´ , - проекция вектора перемещения на направление вектора силы.

Из формулы (1. 30) следует, что работу можно записать как разность значений потенциальной энергии в начальной и конечной точках Величина константы в потенциальной энергии не влияет на физические свойства. Выберем ее так, чтобы при удалении заряда q´ от заряда q на бесконечность потенциальная энергия обращалась в нуль, тогда const = 0 и получаем (1. 31)

Будем теперь рассматривать заряд q´ как пробный заряд, с помощью которого изучается электрическое поле заряда q. Составим отношение. Оно уже не зависит от величины пробного заряда и поэтому характеристикой электрического поля заряда q является (1. 32) - называется потенциалом электрического поля в точке r.

Как видно из формулы (1. 32), потенциал численно равен потенциальной энергии, которой обладал бы в данной точке поля единичный положительный пробный заряд. Поэтому потенциал – является энергетической характеристикой электрического поля. Если имеется система зарядов q 1, q 2 , …, q. N, то из принципа суперпозиции вытекает, что потенциал суммарного электрического поля системы равен сумме потенциалов электрических полей отдельных зарядов (1. 33) где - r 1, r 2 , …, r. N - расстояния от зарядов до выбранной точки поля.

Из формулы (1. 32) следует, что некоторый заряд q, находящийся в точке поля с потенциалом имеет потенциальную энергию (1. 34) а работа сил поля, совершаемая при перемещении этого заряда из точки 1 в точку 2, пропорциональна убыли потенциала (1. 35)

Если заряд q перемещается в точку 2, находящуюся на бесконечности, то и значит Следовательно потенциал равен работе, совершаемой силами электрического поля над единичным положительным зарядом при перемещении его из данной точки на бесконечность. Такую же по величине работу надо совершить против сил электрического поля, чтобы переместить единичный положительный заряд из бесконечности в заданную точку поля.

За единицу электрического потенциала принимается потенциал в такой точке поля для перемещения в которую из бесконечности положительного заряда величиной в 1 Кл необходимо совершить работу, равную 1 Дж. Эта единица называется вольтом Для характеристики энергий микрочастиц часто используется вспомогательная единица энергии – электронвольт (э. В). Электронвольт равен работе, совершаемой силами электрического поля над элементарным зарядом при его перемещении между двумя точками, разность потенциалов которых составляет 1 В

11. Связь между потенциалом и напряженностью электрического поля. Электрическое поле можно описать с помощью двух величин – вектором напряженности и потенциалом. Между ними существует связь, найдем ее. Для этого используем выражение для силы , действующей на заряд q в электрическом поле. С одной стороны эта сила равна С другой стороны для консервативных сил Приравнивая, получаем (1. 36)

или в декартовых проекциях (1. 37)