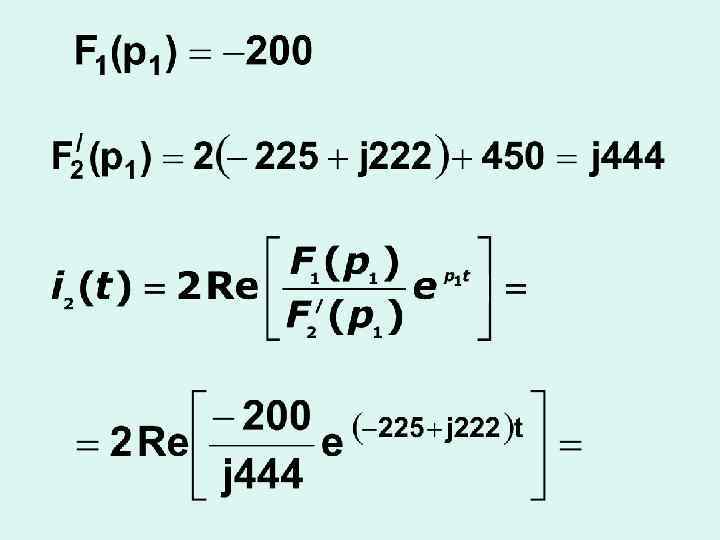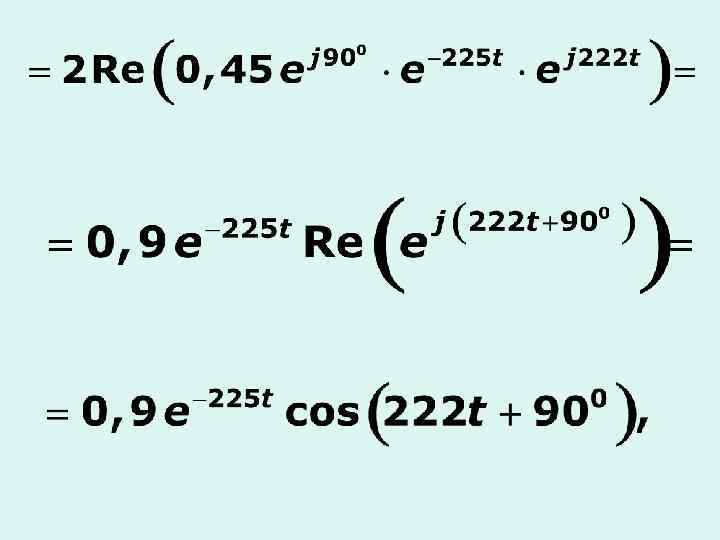V Переходные процессы в линейных электрических цепях

V Переходные процессы в линейных электрических цепях

5. 1 Переходный режим электрических цепей. Законы коммутации

• Переходный процесс – режим работы электрической цепи, возникающий при переходе цепи из одного установившегося состояния в другое установившееся состояние • Коммутация – любое изменение параметров цепи, ее конфигурации, подключение или отключение источников, приводящее к возникновению переходных процессов

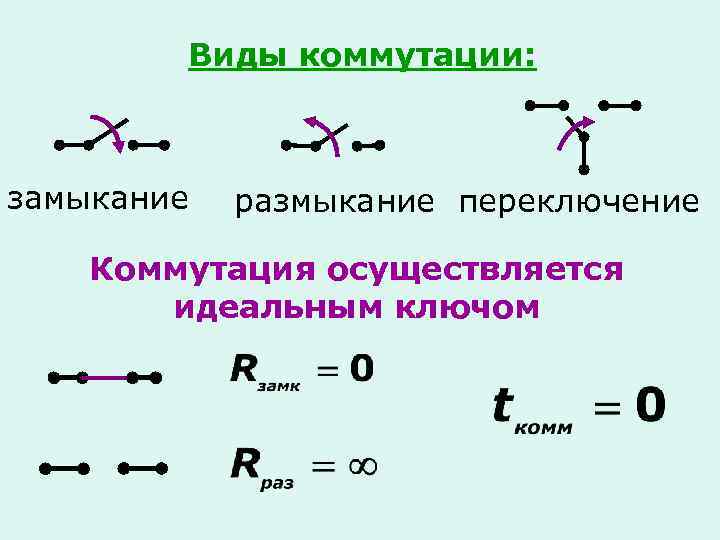Виды коммутации: замыкание размыкание переключение Коммутация осуществляется идеальным ключом

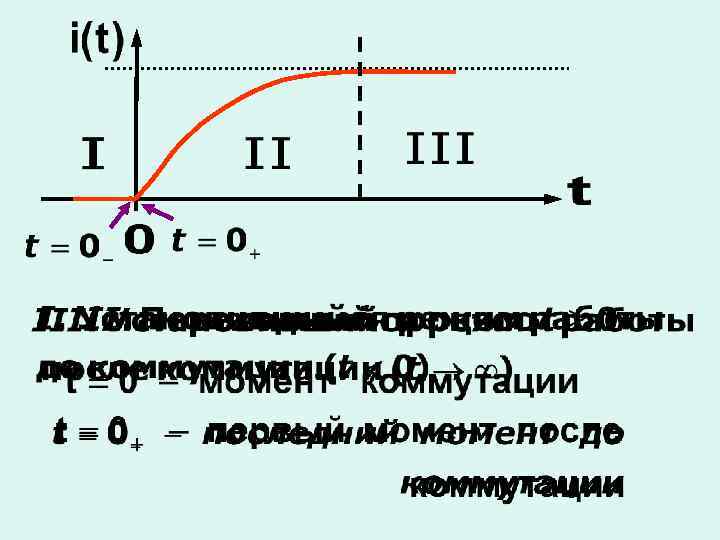
Переходный процесс возможен в цепях, содержащих реактивные элементы

Законы коммутации 1 -ый закон Ток в индуктивности не может измениться скачком 2 -ой закон Напряжение на ёмкости не может измениться скачком

Начальные условия - значения токов и напряжений в момент t=0+ Независимые начальные условия – не изменяются в момент коммутации – ННУ Определяют из схемы до коммутации

Зависимые начальные условия – могут изменяться в момент коммутации –ЗНУ Определяют по законам Кирхгофа из схемы после коммутации Начальные условия могут быть нулевыми и ненулевыми

установившийся режим значения токов и напряжений называются принужденными Теоретически переходный процесс длится бесконечно долго, практически - постоянная времени цепи (характеризует скорость протекания ПП) – время, в течение которого свободная составляющая затухает в е раз

5. 2 Классический метод расчета переходных процессов

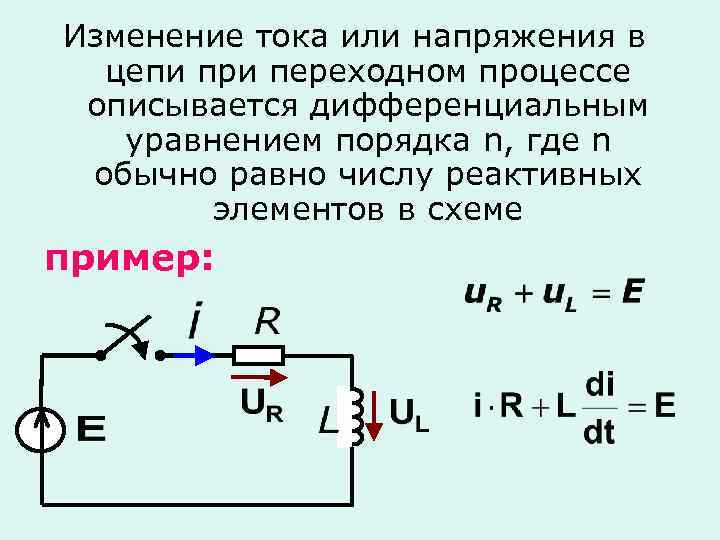Изменение тока или напряжения в цепи при переходном процессе описывается дифференциальным уравнением порядка n, где n обычно равно числу реактивных элементов в схеме пример:

- независимая переменная - неоднородное диф. уравнение 1 -го порядка - характеристическое уравнение 1 -го порядка

Решение линейного неоднородного дифференциального уравнения состоит из двух решений: характеризует свободные - характеризует принужденные процессы, происходящие в процессы от внешнего электрической цепи при воздействия при отсутствии внешнего воздействия (частное решение уравнения) (общее решение уравнения)

Способ составления характеристического уравнения цепи: а) нарисовать схему для времени б) удалить источники энергии, заменив их внутренними сопротивлениями (источник напряжения - КЗ, источник тока - ХХ) в) выполнить замену

г) разорвать цепь в любом удобном месте и определить входное сопротивление д) уравнение - характеристическое Характеристическое уравнение определяется только конфигурацией схемы

Порядок расчета переходных процессов классическим методом 1. Задать направления токов 2. Определить начальные условия а) ННУ при б) ЗНУ при 3. Определить принужденную составляющую

4. Записать характеристическое уравнение и найти его корни 5. Зная корни, записать общее решение 6. Для используя начальные условия, определить неизвестные постоянные интегрирования

7. Записать закон изменения и выполнить проверку при и 8. Построить графики

5. 3 Переходные процессы в цепях I порядка

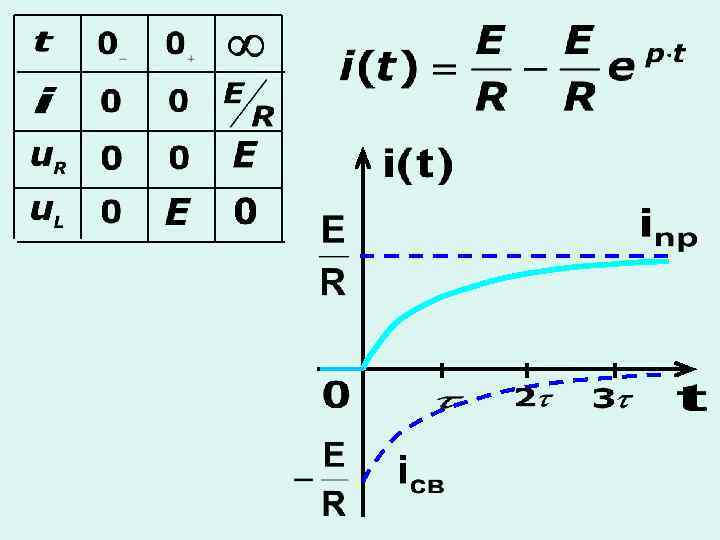
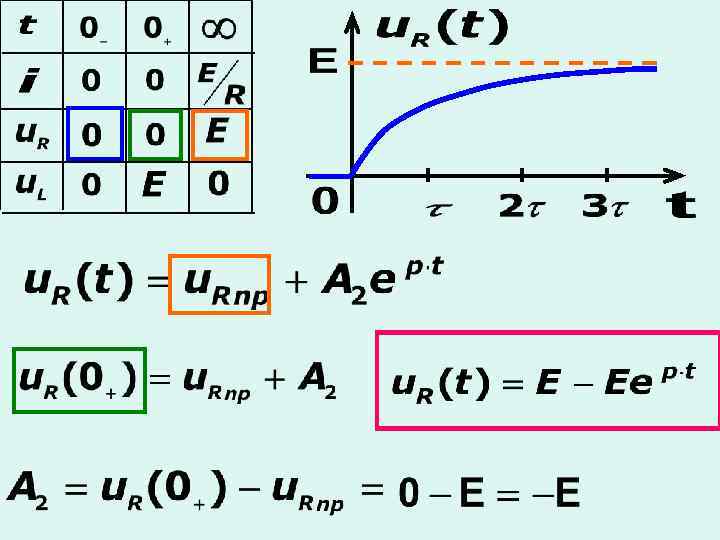
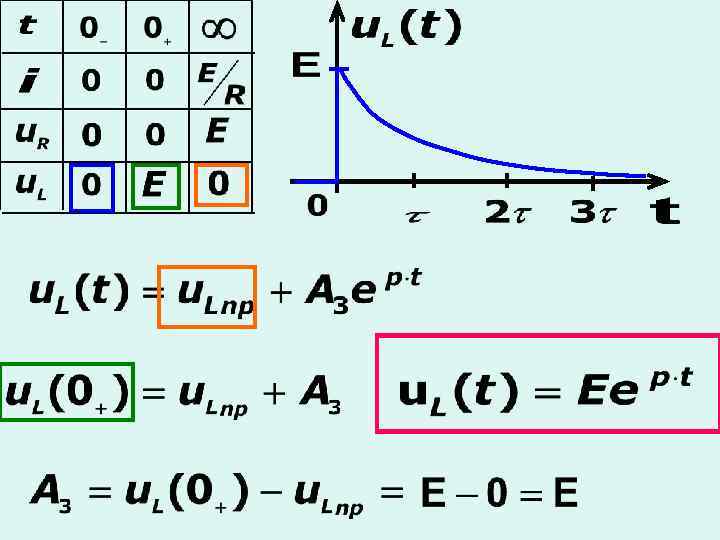
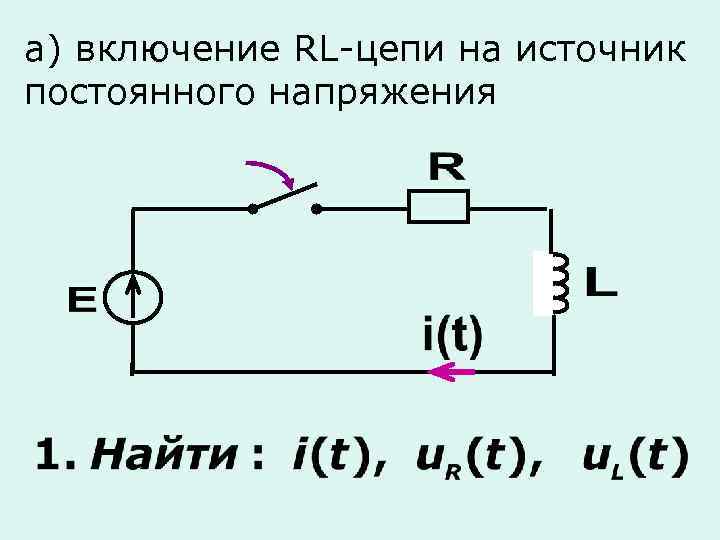а) включение RL-цепи на источник постоянного напряжения

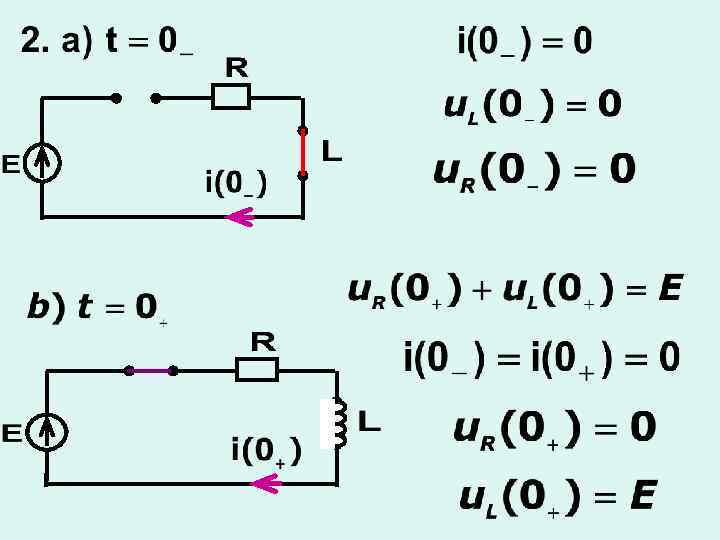
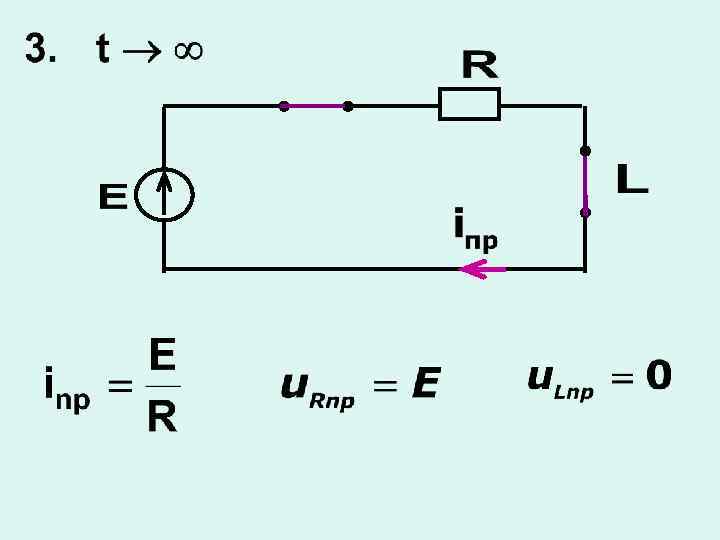
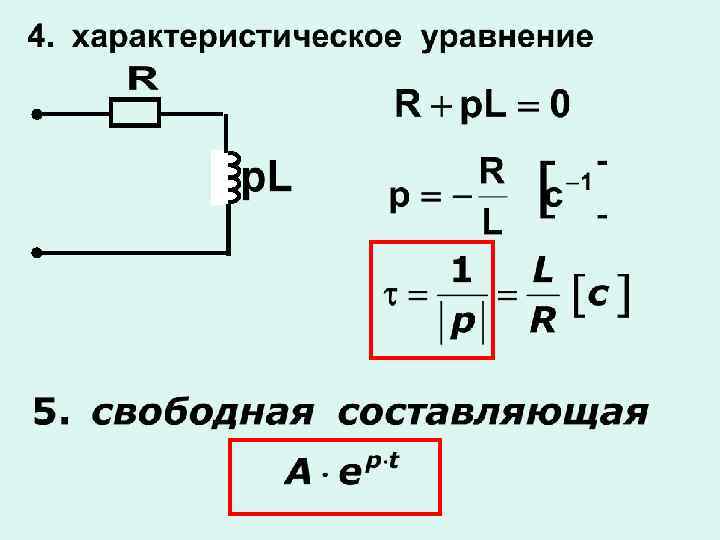
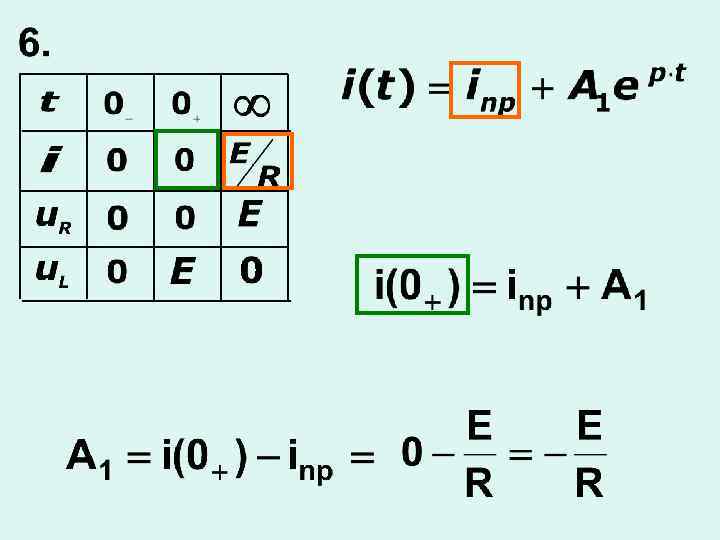
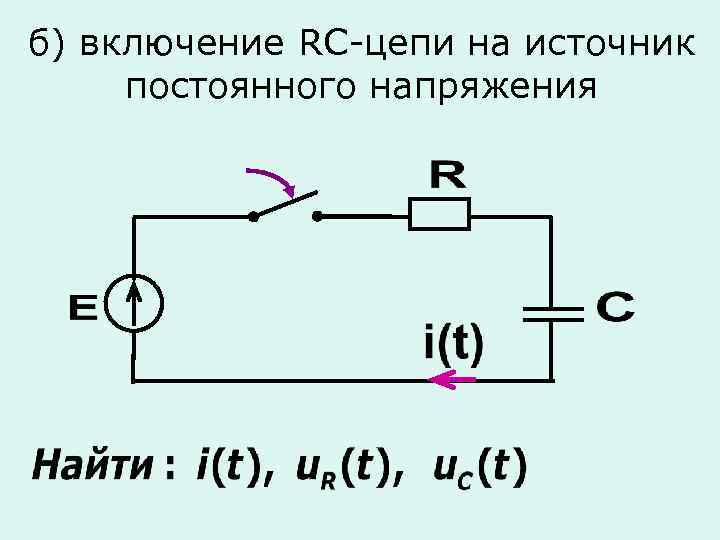б) включение RС-цепи на источник постоянного напряжения

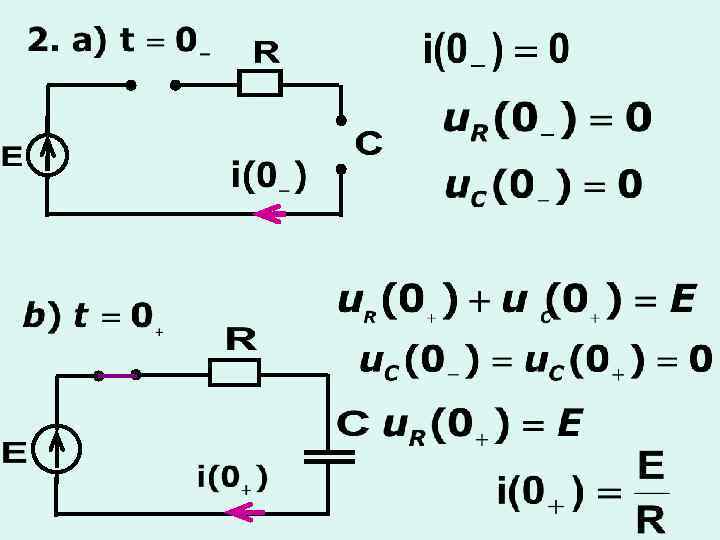
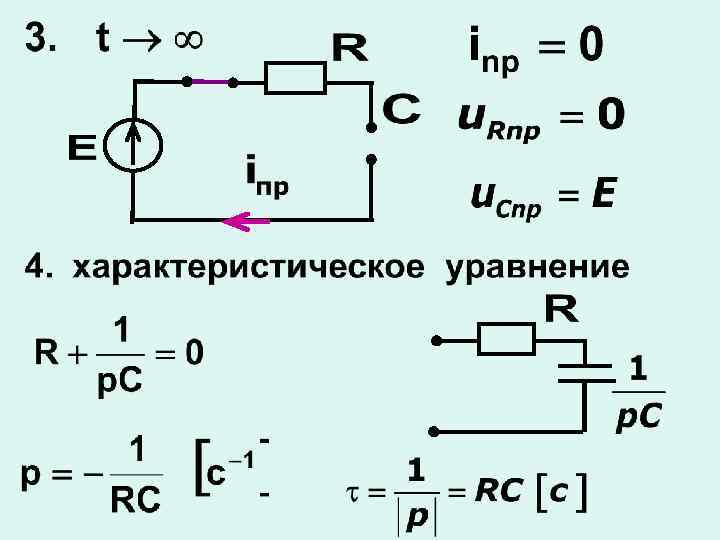
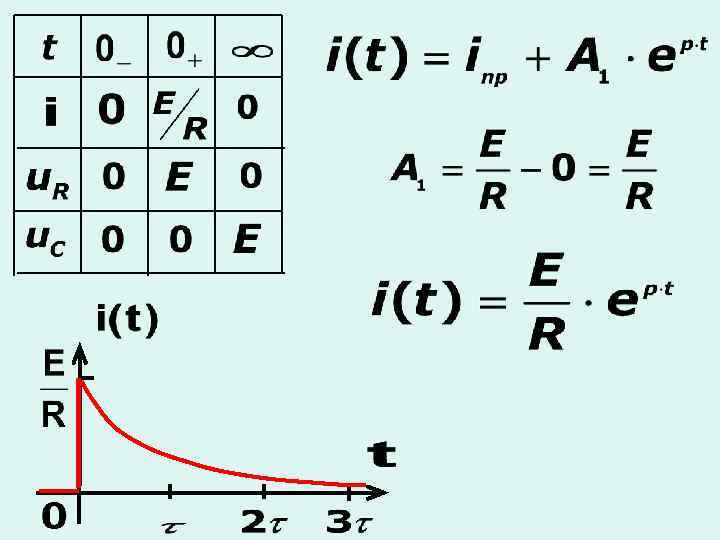
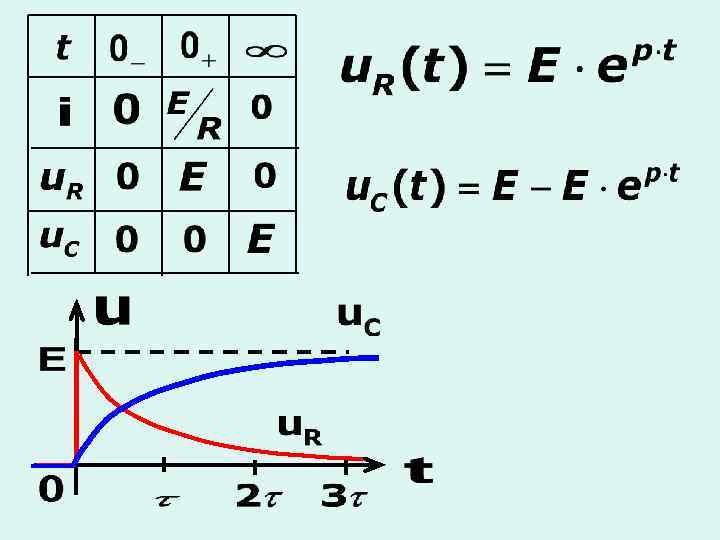
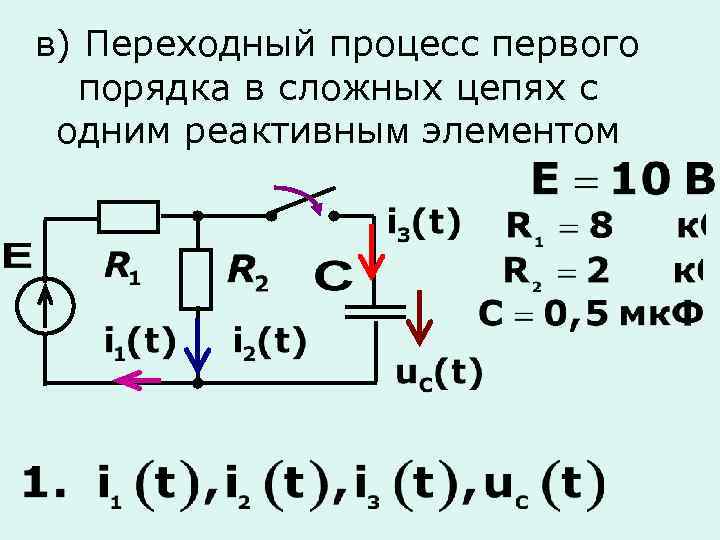в) Переходный процесс первого порядка в сложных цепях с одним реактивным элементом

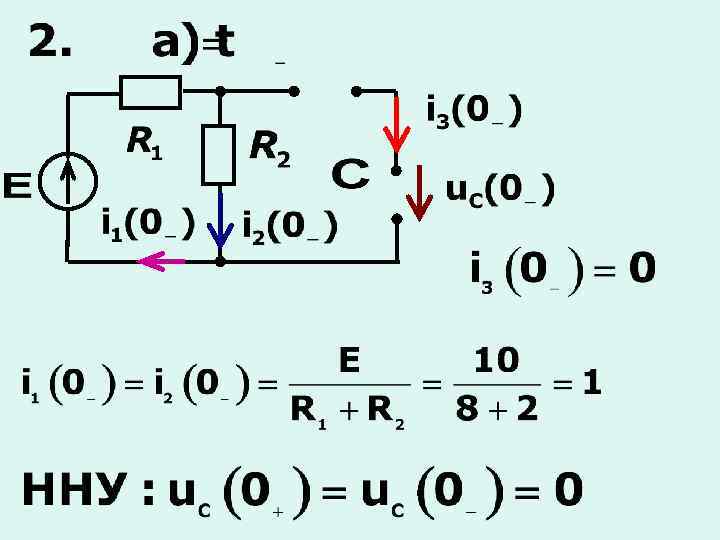
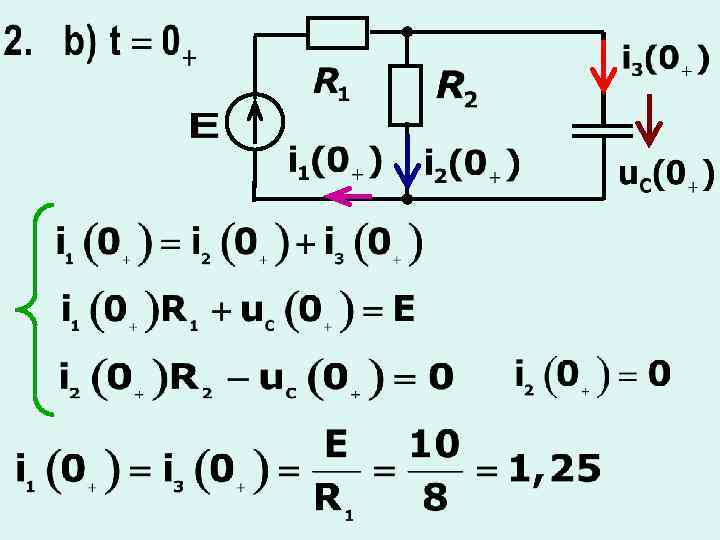
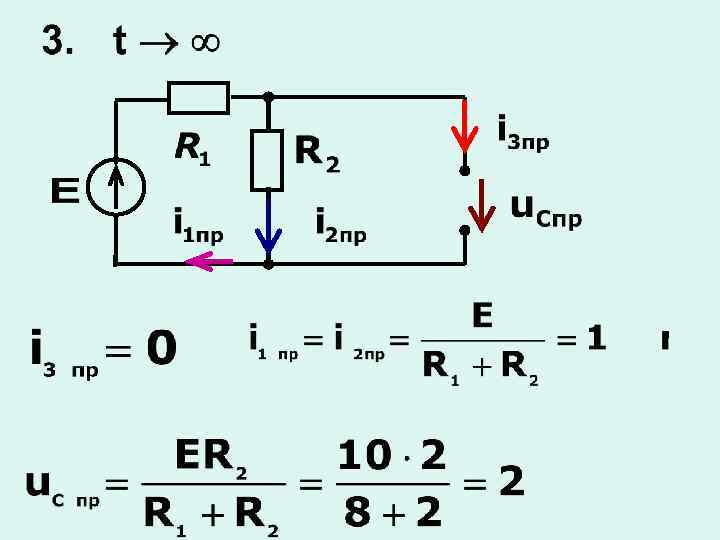
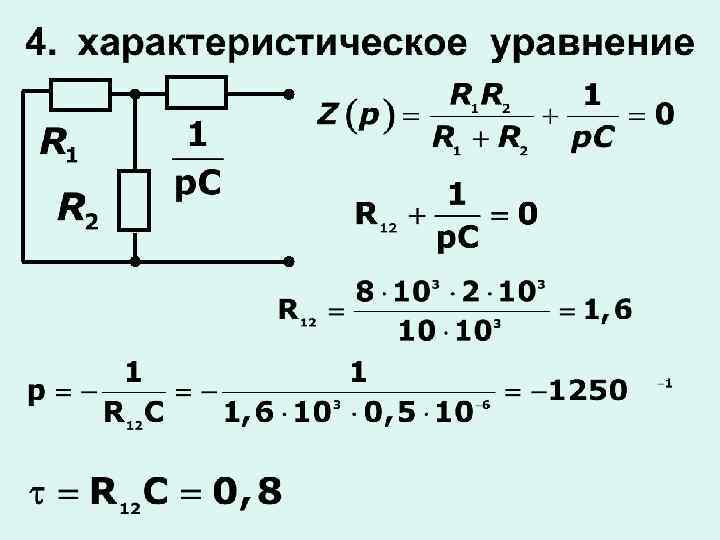
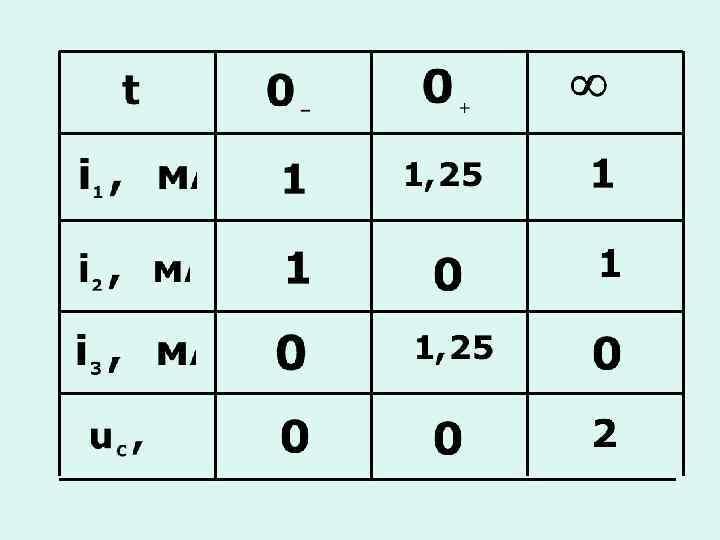
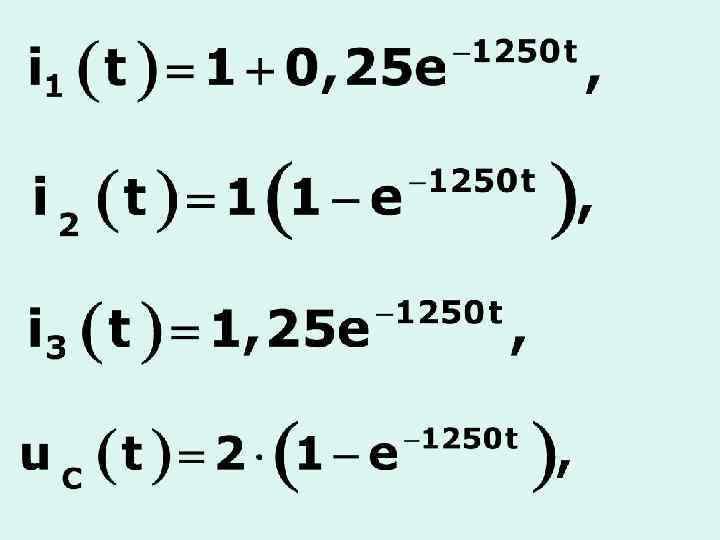
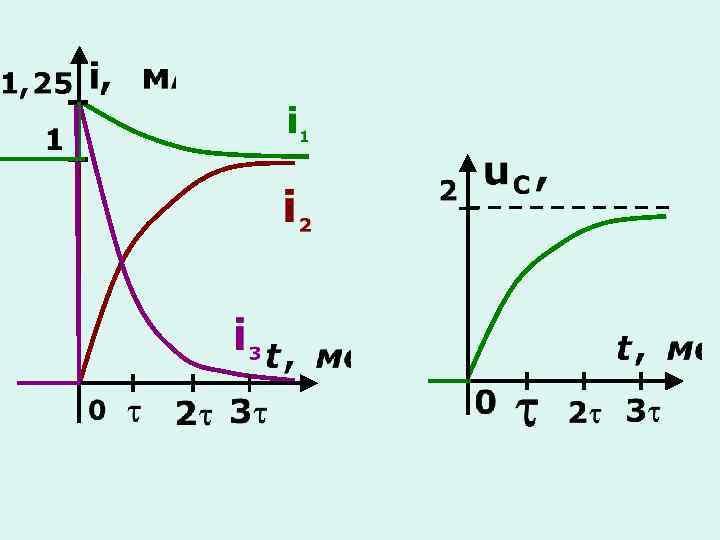
5. 4 Переходные процессы в цепях второго порядка

Особенности расчета • В момент коммутации определяют два независимых начальных условия: • Наряду с определением зависимых начальных условий определяют производные токов и напряжений

Характеристическое уравнение вида Решение имеет два корня

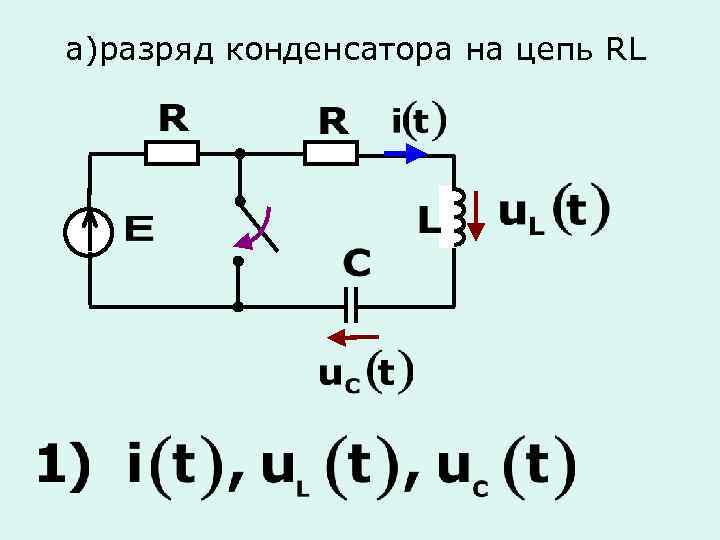а)разряд конденсатора на цепь RL

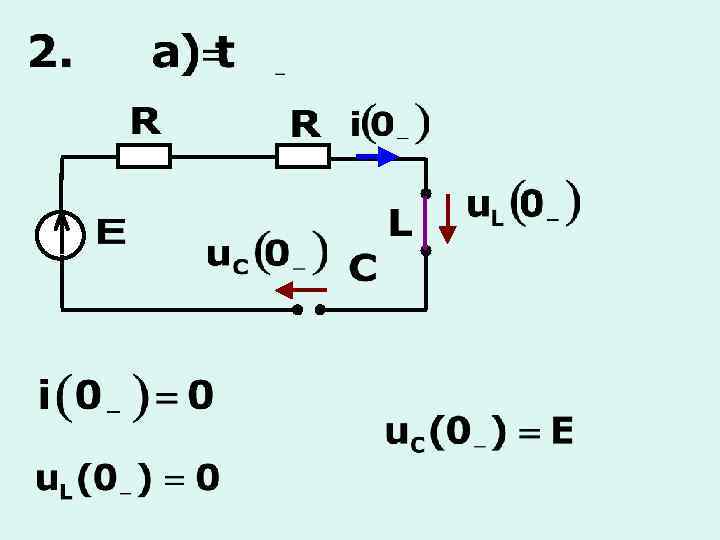
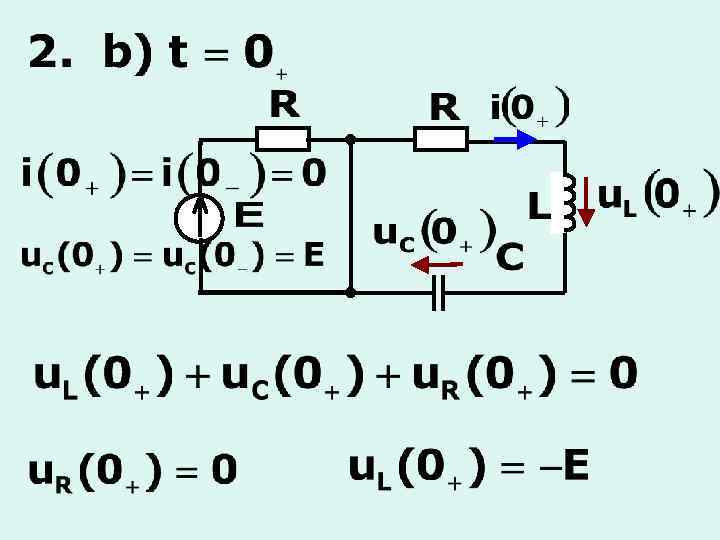
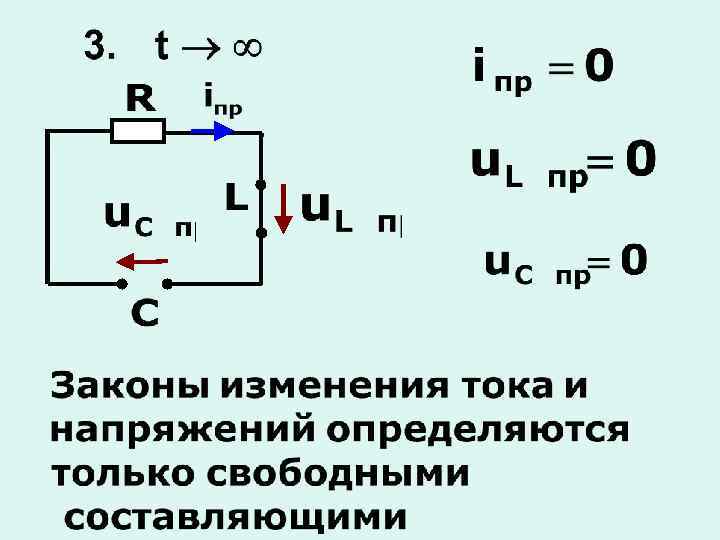
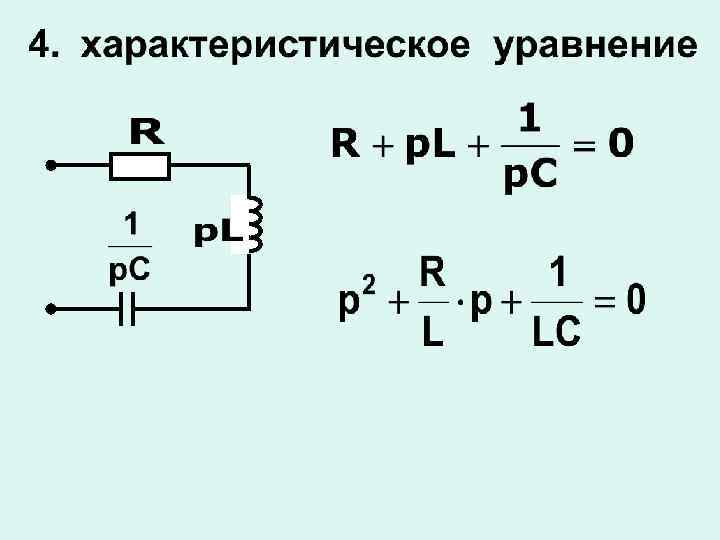
1. Апериодический процесс Корни и разные и - вещественные

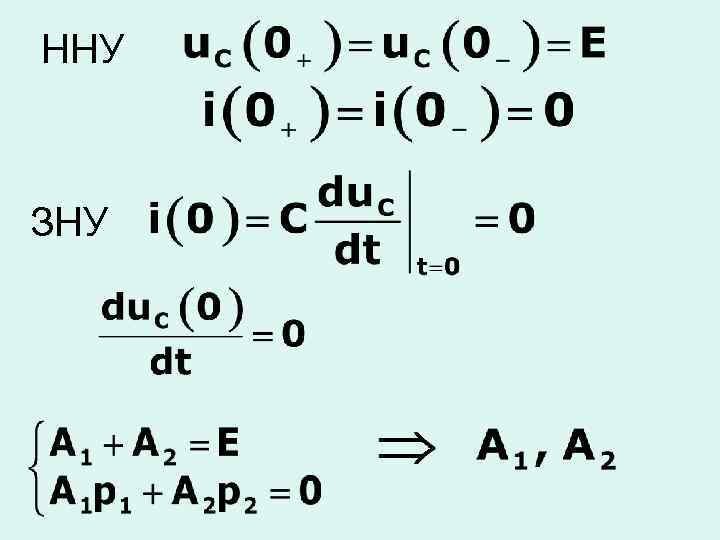ННУ ЗНУ

2. Колебательный процесс Корни и сопряженные - комплексно-

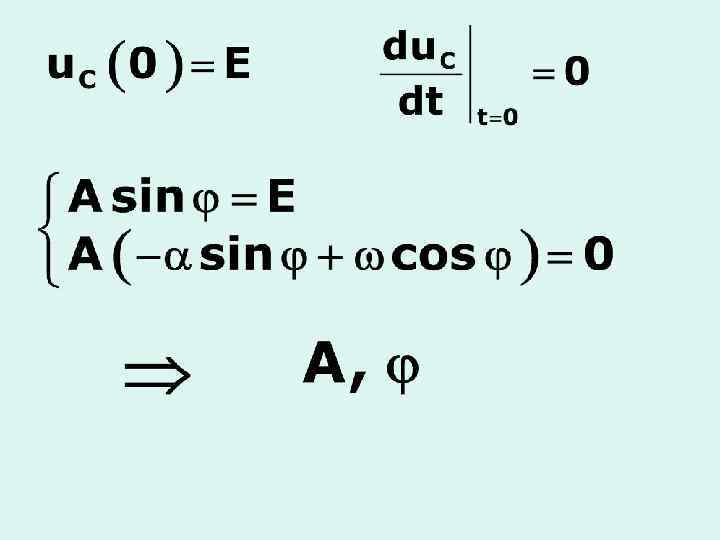
3. Критический процесс вещественны и равны

графики зависимостей аналогичны кривым апериодического процесса с той разницей, что скорость изменения их увеличилась

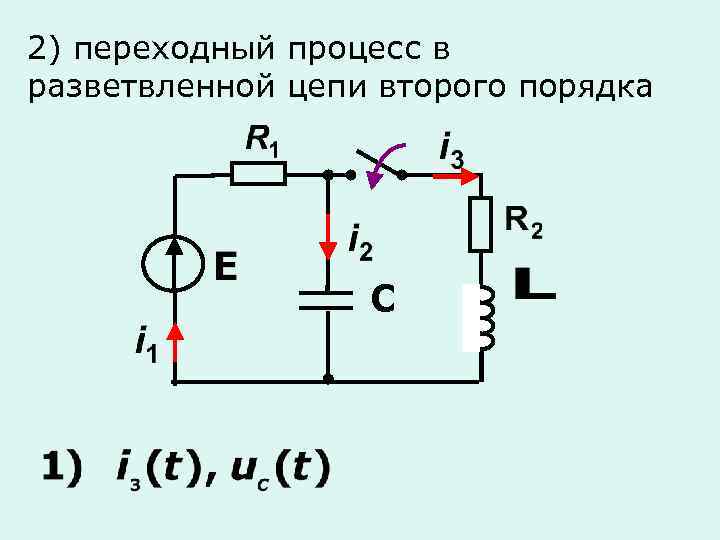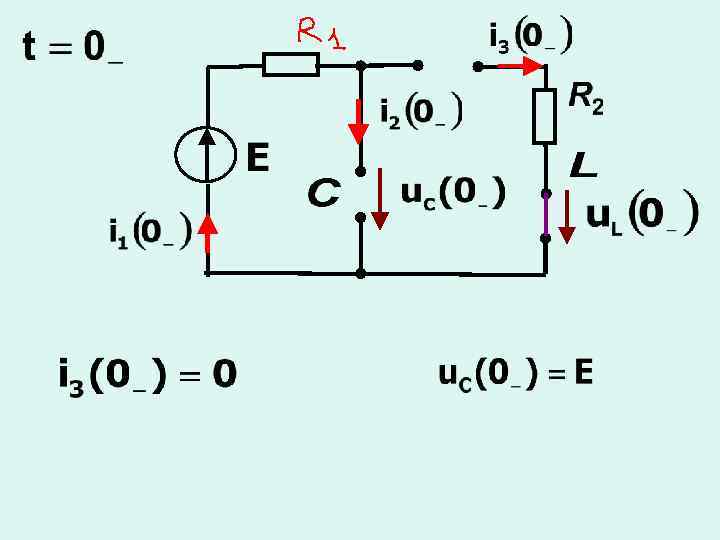
2) переходный процесс в разветвленной цепи второго порядка С

С

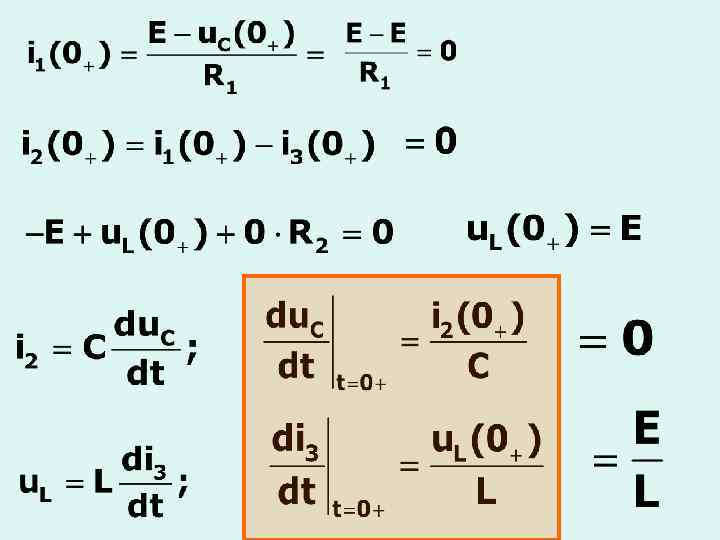
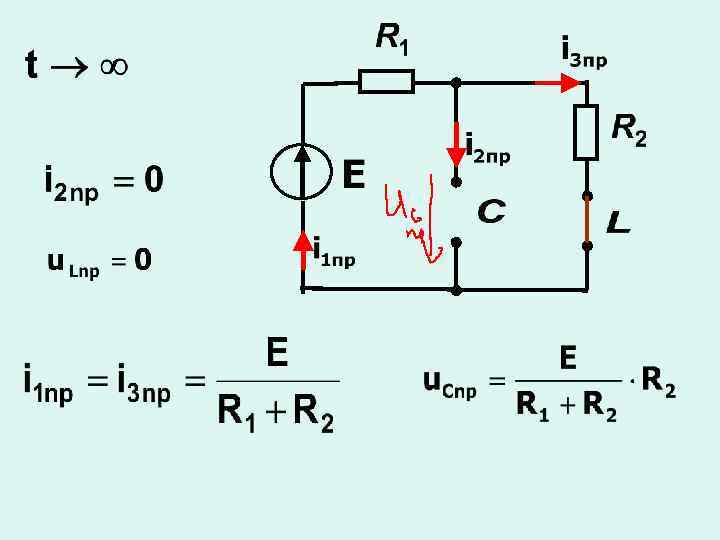
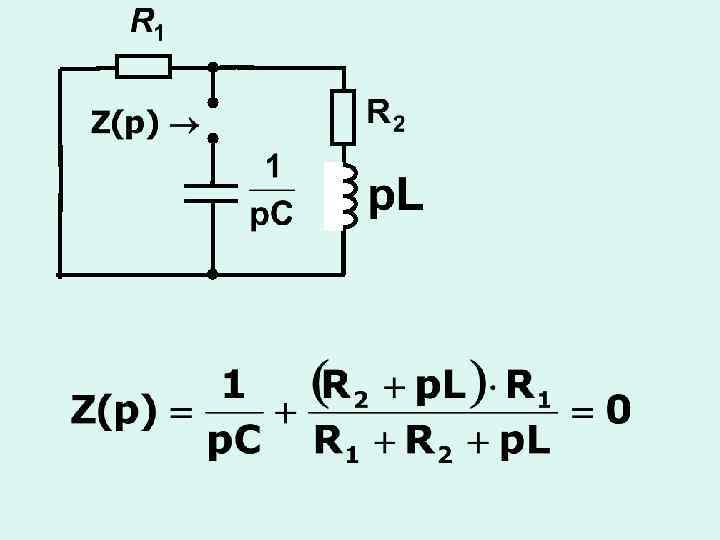
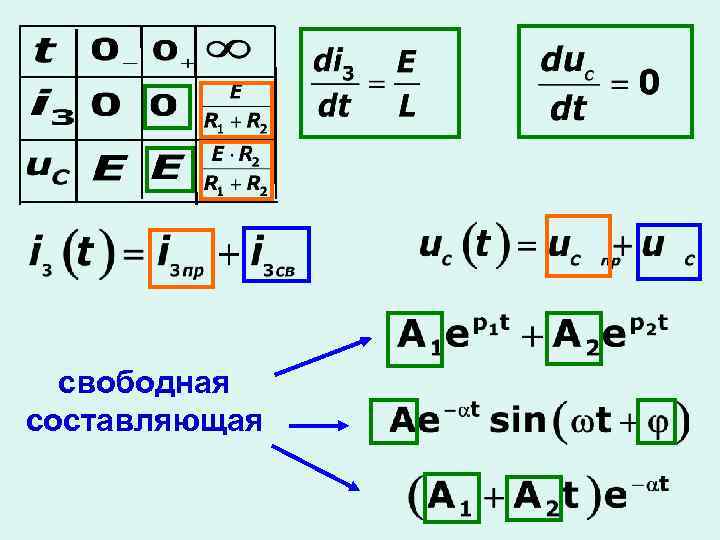свободная составляющая

7. 5 Операторный метод расчета. Основные положения.

Базируется на преобразованиях Лапласа, которые позволяют систему дифференциальных уравнений свести к системе алгебраических уравнений

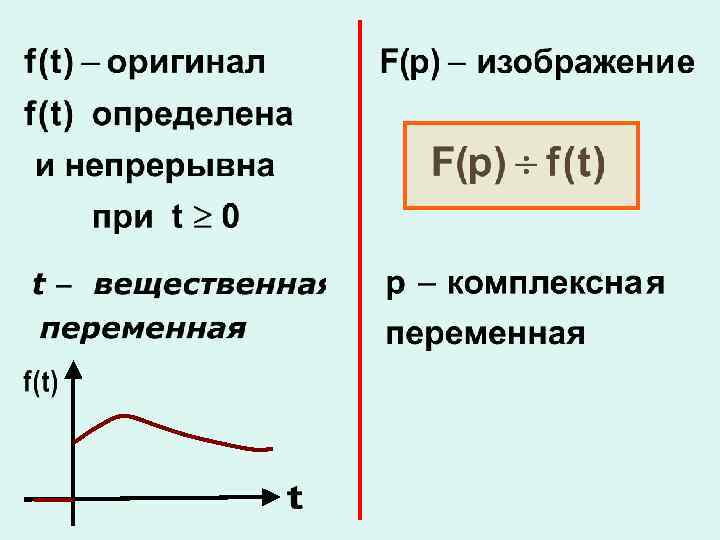
Преобразования Лапласа прямое: обратное:

Основные свойства преобразования Лапласа 1. Линейность 2. Теорема запаздывания

3. Дифференцирование оригинала - нулевые начальные условия - ненулевые начальные условия

4. Интегрирование оригинала - нулевые начальные условия - ненулевые начальные условия

5. Теорема подобия 6. Теорема смещения

7. Теорема свертки

8. Предельные соотношения а) б)

Изображения наиболее часто встречающихся функций 1. единичная функция

2. Импульсная функция (функция Дирака) физически нереализуемая функция (математическая абстракция)

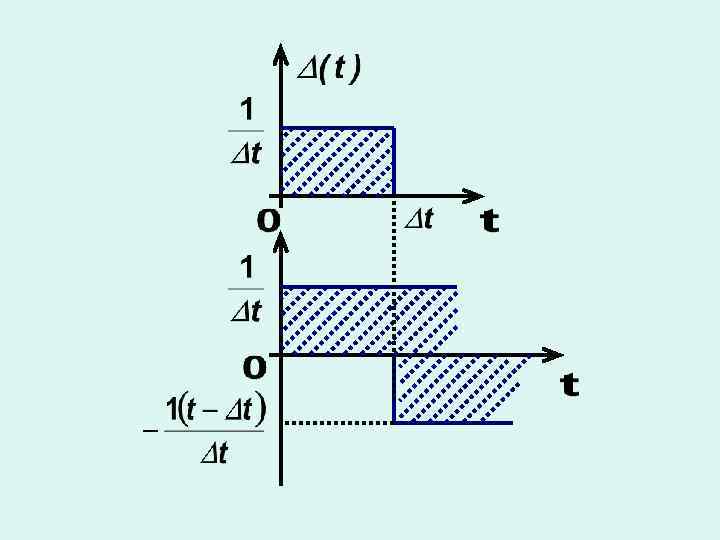
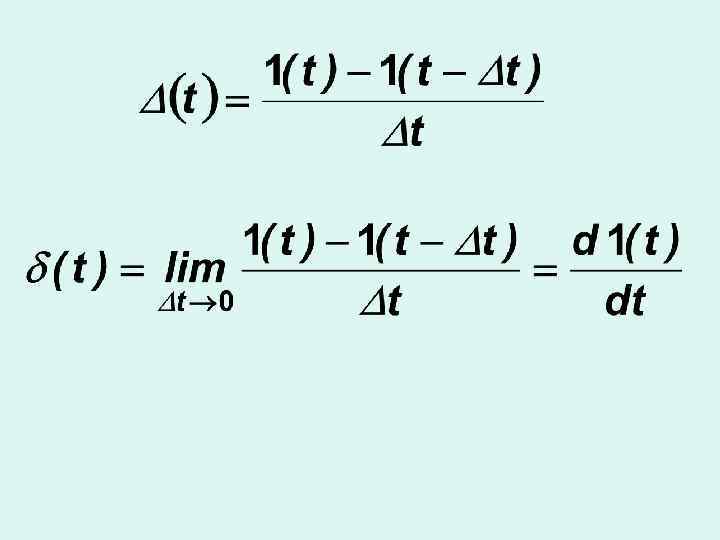
Свойства -функции 1. 2. фильтрующее свойство

Таблица оригиналов и их изображений

Законы Ома и Кирхгофа в операторной форме 1. Сопротивление

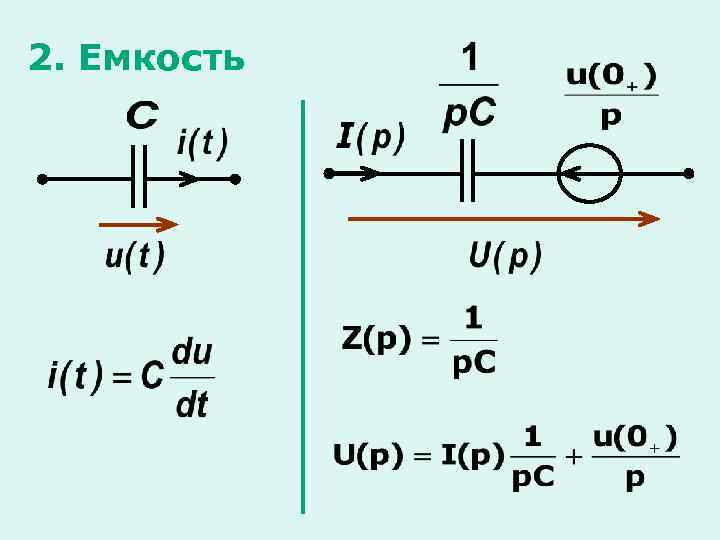2. Емкость

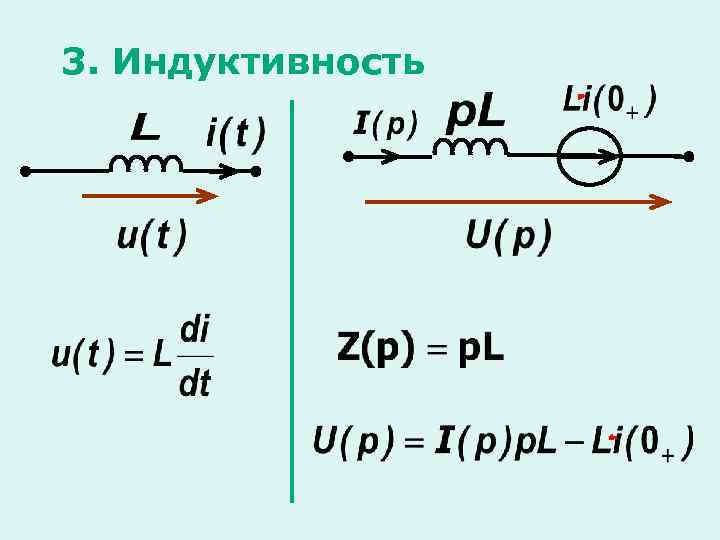3. Индуктивность

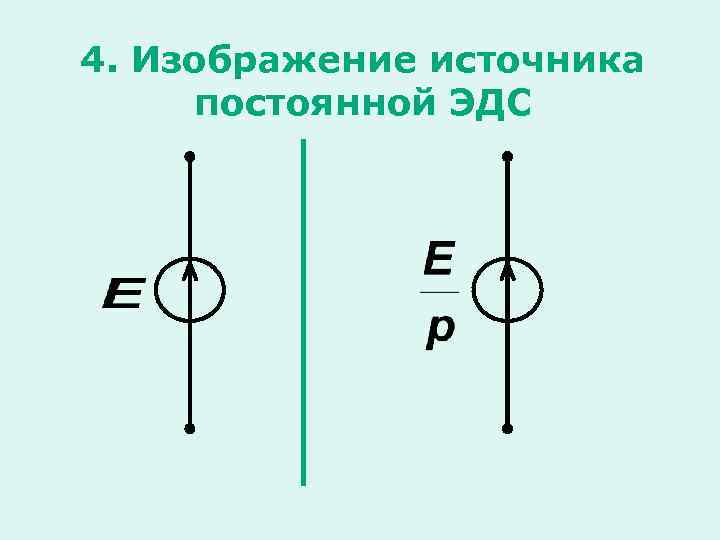4. Изображение источника постоянной ЭДС

Законы Кирхгофа

Операторная передаточная функция – отношение изображения выходной реакции цепи к изображению входного воздействия

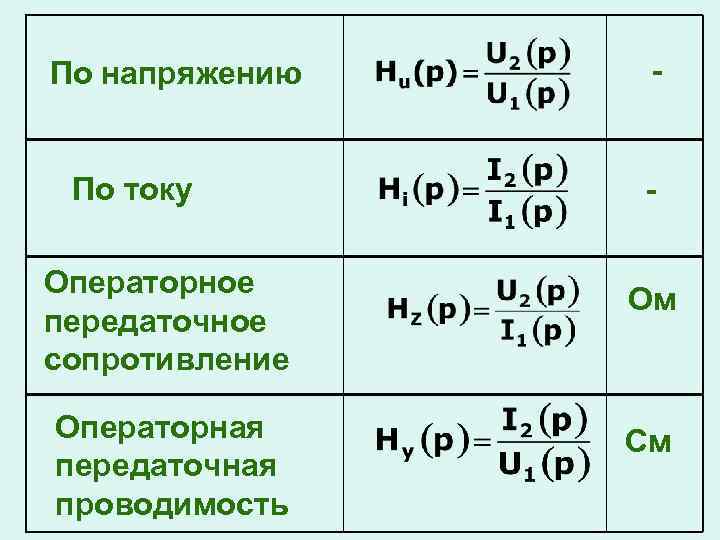- По напряжению По току - Операторное передаточное сопротивление Операторная передаточная проводимость Ом См

Представление операторной передаточной функции: 1. В виде дробнорациональной функции

2. В виде отношения произведений нулей и полюсов функции ноль функции полюс функции

Комплексную передаточную функцию можно получить из операторной передаточной функции , заменив в p на j

7. 6 Расчет переходных процессов операторным методом

Алгоритм расчета: • Обозначить токи в ветвях • Определить независимые начальные условия • Составить операторную схему замещения • Используя любые методы расчета, записать изображение искомой величины • Выполнить обратное преобразование Лапласа

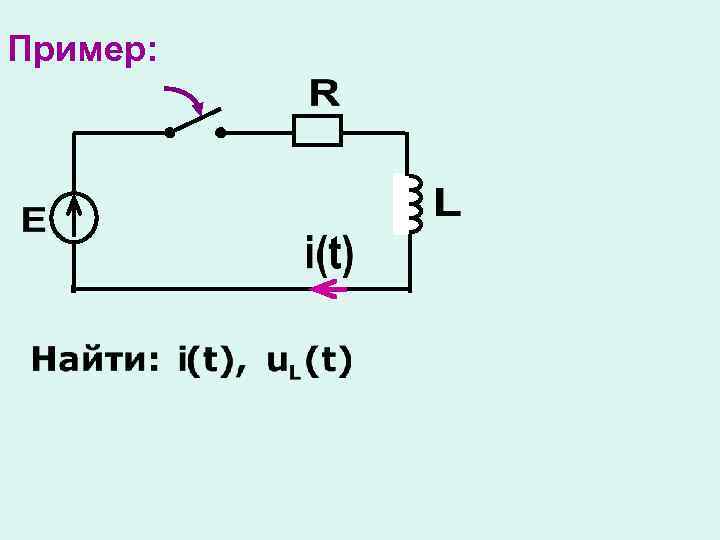Пример:

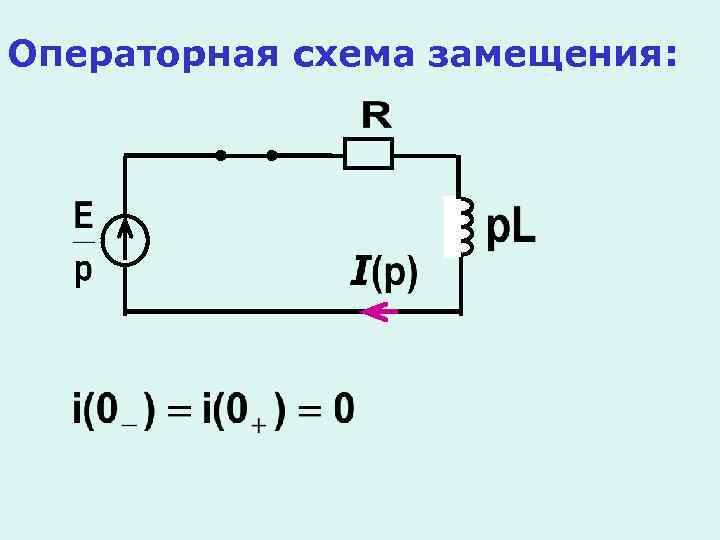Операторная схема замещения:

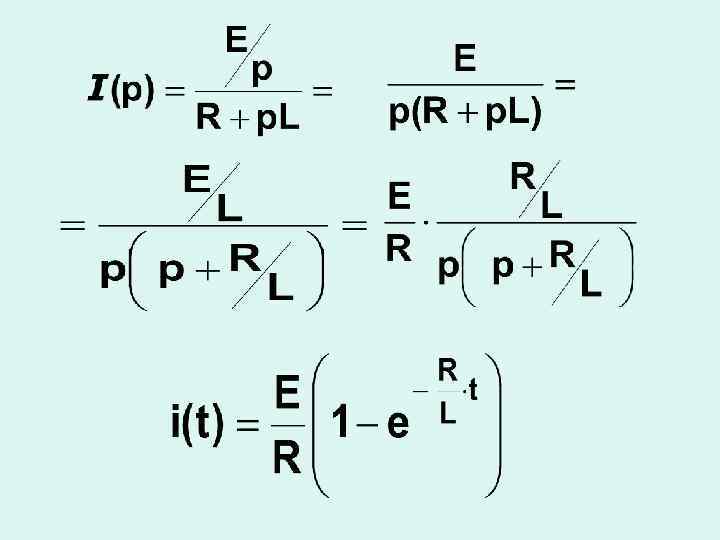
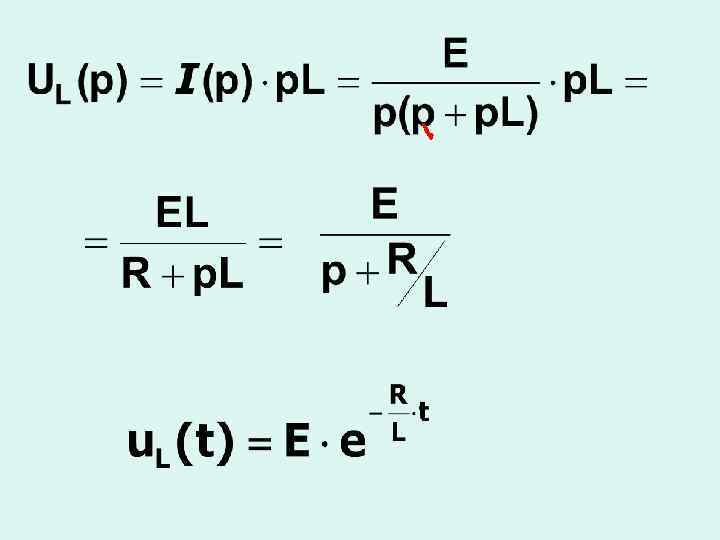
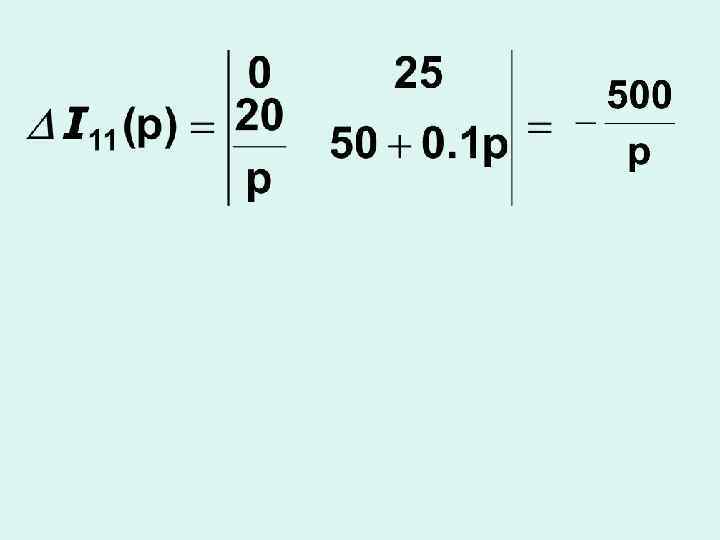
Теорема разложения - как один из методов перехода от изображения к оригиналу функции.

В зависимости от вида полюсов формула разложения имеет различный вид. Для двух полюсов:

2) полюсы комплексно-сопряженные

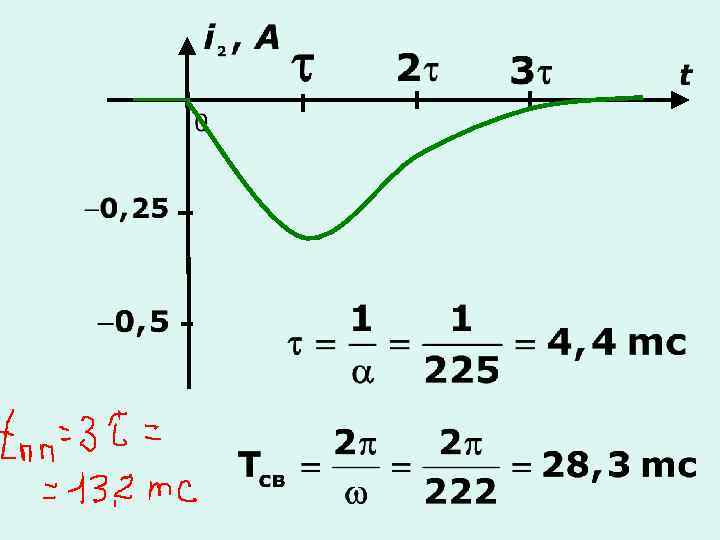
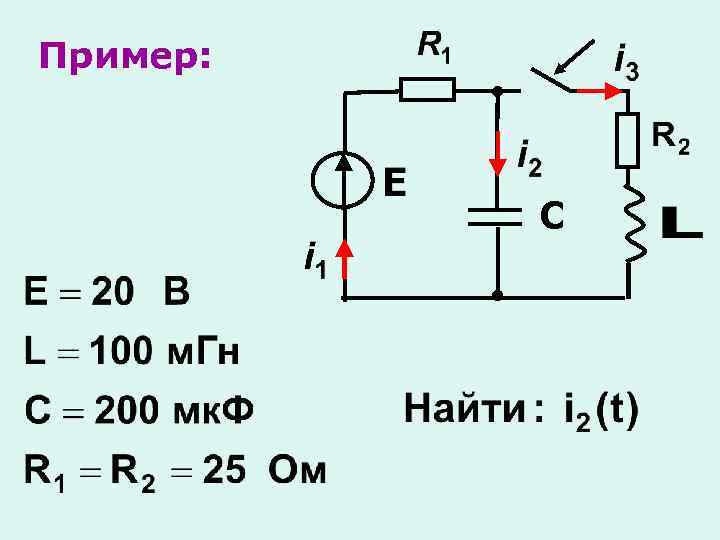Пример: С

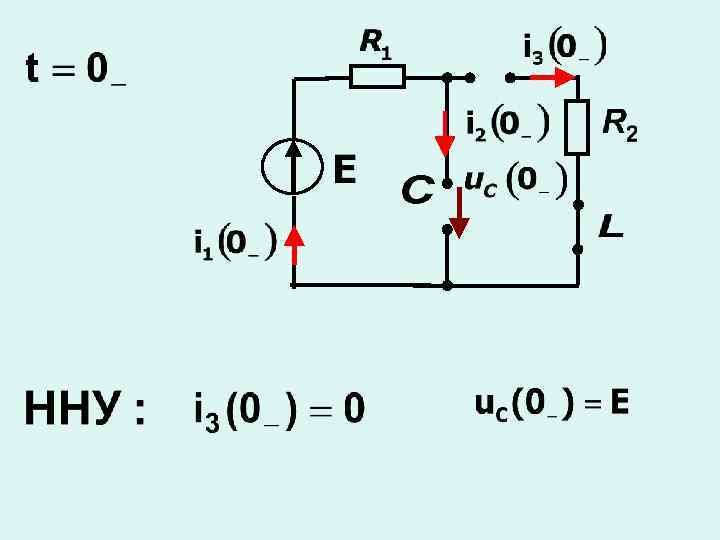
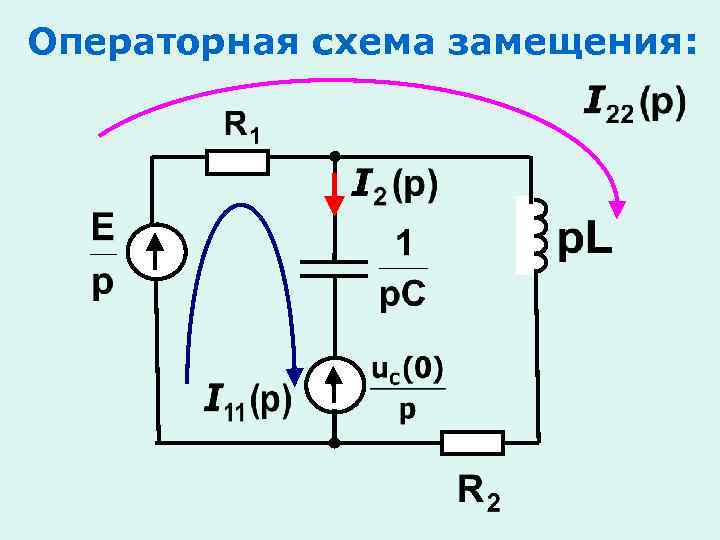Операторная схема замещения: