Геометрия - торетический курс 7-9..pptx
- Количество слайдов: 10
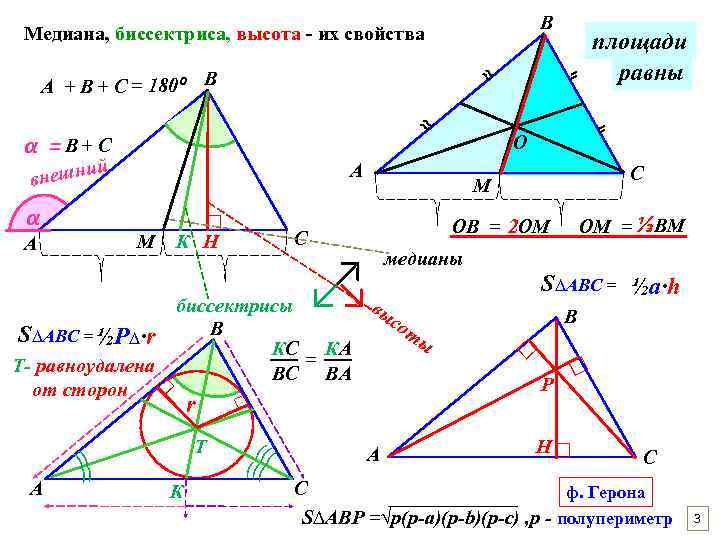
В Медиана, биссектриса, высота - их свойства ≈ А + В + С = 180⁰ В ≈ α =В+ С ий внешн М А А )) )) медианы ↗ ↙↘ вы биссектрисы В КC КA = BC BA □ Т- равноудалена от сторон r Т К ОМ = ⅓BМ ОВ = 2 ОМ С К Н С М S∆ABC = ½а∙h В со ты □ S∆ABC = ½P∆∙r □ ⸗ О А P □ )) ) α площади равны ⸗ А Н □ □ С С ф. Герона S∆ABP =√p(p-a)(p-b)(p-c) , p - полупериметр 3
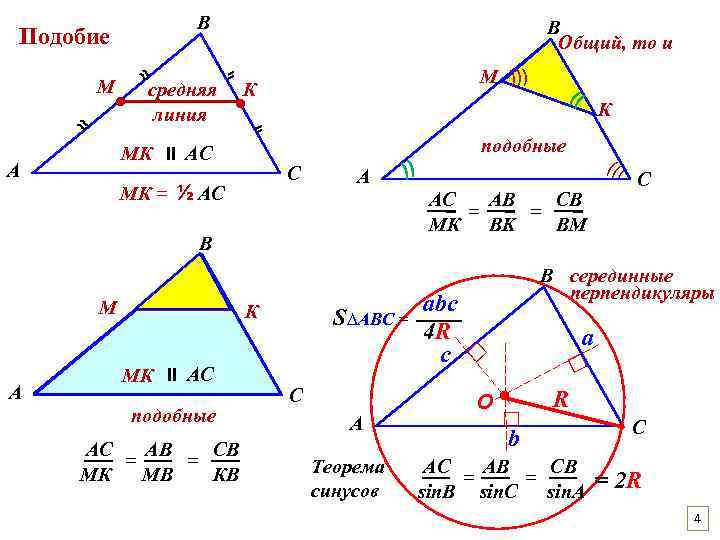
В Подобие ⸗ средняя К ● линия МК = ⸗ С ½ АС А М АС AВ СВ = = МК BK BМ подобные АС AВ СВ = = МК МB КB S∆ABC = С А Теорема синусов С В серединные перпендикуляры abc 4 R c a □ □ А К МК ӀӀ АС подобные )) В К ) )) МК ӀӀ АС А М ))) )) ≈ М ● ≈ В Общий, то и О● □ R b АС AВ СВ = = sin. B sin. C sin. A С = 2 R 4
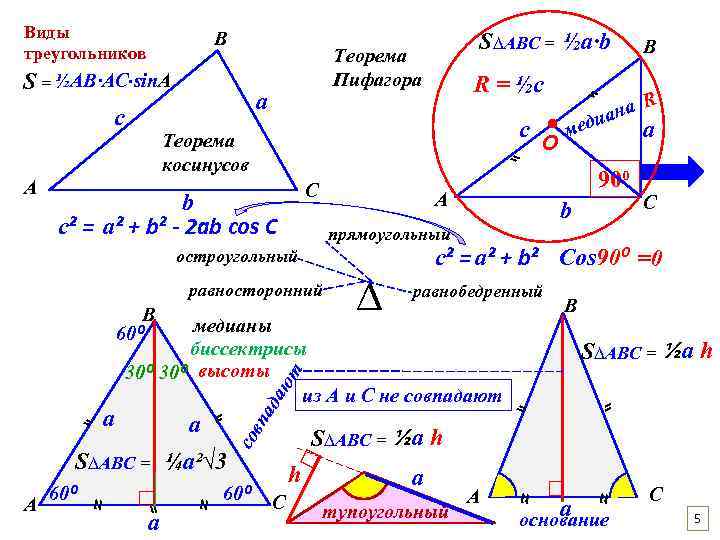
Виды треугольников В S = ½AB∙AC∙sin. A а иан c ● мед О Теорема косинусов С b с² = a² + b² - 2 ab cos C 90⁰ А равносторонний В 60⁰ b ∆ равнобедренный со вп ад аю т S∆ABC = ½а h □ h С а тупоугольный А □ ≈ 60⁰ ⸗ S∆ABC = ½а h ≈ а ≈ □ ⸗ ≈ А 60⁰ С В ⸗ ⸗ S∆ABC = ¼а²√ 3 a с² = a² + b² Cos 90⁰ =0 медианы биссектрисы 30⁰ высоты из А и С не совпадают а ⸗ R прямоугольный остроугольный а В ⸗ А a R = ½c ⸗ c S∆ABC = ½а∙b Теорема Пифагора а основание С 5
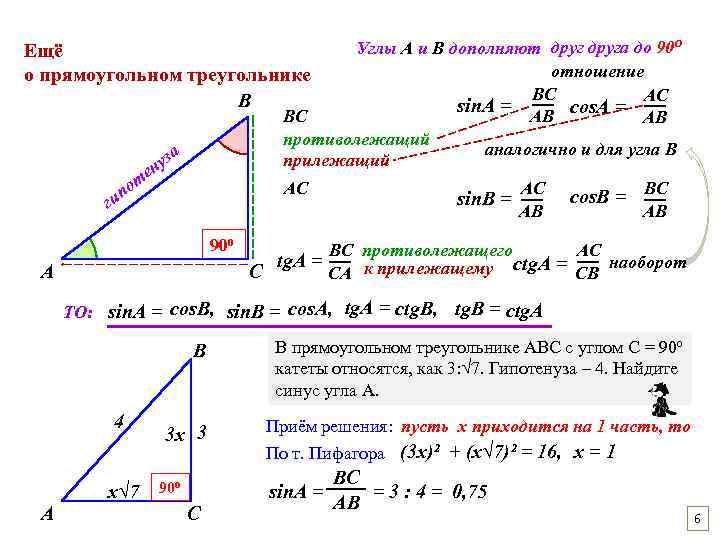
Углы А и В дополняют друга до 90⁰ отношение ВС АС sin. A = ― cos. A = ― ВС АВ АВ противолежащий аналогично и для угла В прилежащий Ещё о прямоугольном треугольнике В а уз н те по АС ги 90⁰ А sin. B = BС противолежащего tg. A = ― к прилежащему С CA AС ― АВ BС cos. B = ― АВ AС ― ctg. A = CB наоборот ТО: sin. A = cos. B, sin. B = cos. A, tg. A = ctg. В, tg. В = ctg. A В 4 х√ 7 А 3 х 3 90⁰ В прямоугольном треугольнике АВС с углом С = 90⁰ катеты относятся, как 3: √ 7. Гипотенуза – 4. Найдите синус угла А. Приём решения: пусть х приходится на 1 часть, то По т. Пифагора (3 х)² + (х√ 7)² = 16, х = 1 sin. A = С BC = 3 : 4 = 0, 75 AB 6
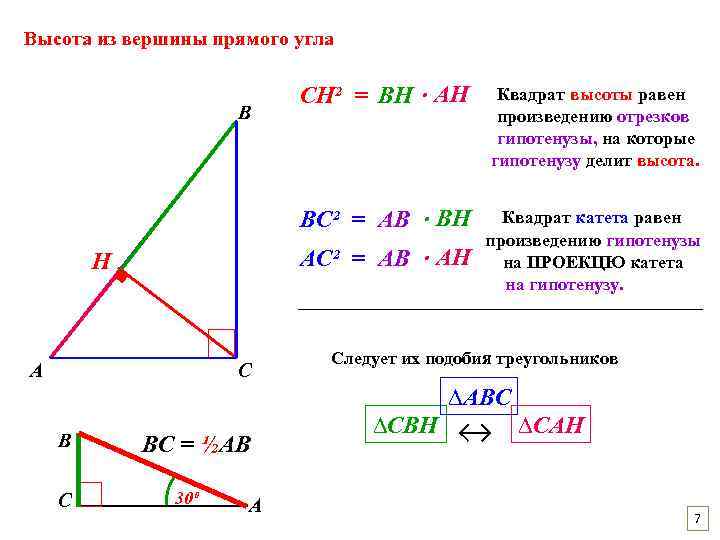
Высота из вершины прямого угла ▪ Квадрат высоты равен произведению отрезков гипотенузы, на которые гипотенузу делит высота. ВС² = АВ ∙ ВН В СН² = ВН ∙ АН Квадрат катета равен произведению гипотенузы на ПРОЕКЦЮ катета на гипотенузу. АС² = АВ ∙ АН Н А С Следует их подобия треугольников ∆АВС В С ВC = ½AВ 30⁰ А ∆СВН ↔ ∆САН 7
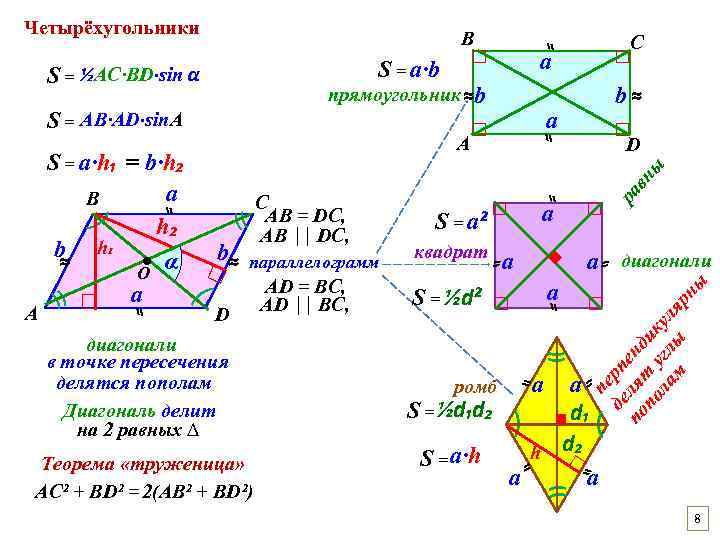
Четырёхугольники В а □ □ D ра вн ы ▪ )) ны )□ □ пе де рп по лят енд по у ик ла гл ул м ы яр ⸗ ⸗а а ⸗ диагонали а⸗ S = ½d₁d₂ d₁ ) h d₂ а∙h □ S= а а ромб ⸗ Теорема «труженица» АС² + ВD² = 2(АB² + ВD²) а S = ½d² □ )) диагонали в точке пересечения делятся пополам Диагональ делит на 2 равных ∆ а ⸗ D АD = BC, АD ││ BC, квадрат □ ) )) параллелограмм а ▪ b≈ S= □ а² ⸗ С АB = DC, АB ││ DC, ⸗ ⸗ ⸗ b≈ ⸗ А ) А а прямоугольник ≈b S = AB∙AD∙sin. A С □ ⸗ S = а∙b S = ½AC∙BD∙sin α S = а∙h₁ = b∙h₂ а В h₂ b h₁ ● α ≈ O а )) □ □ 8
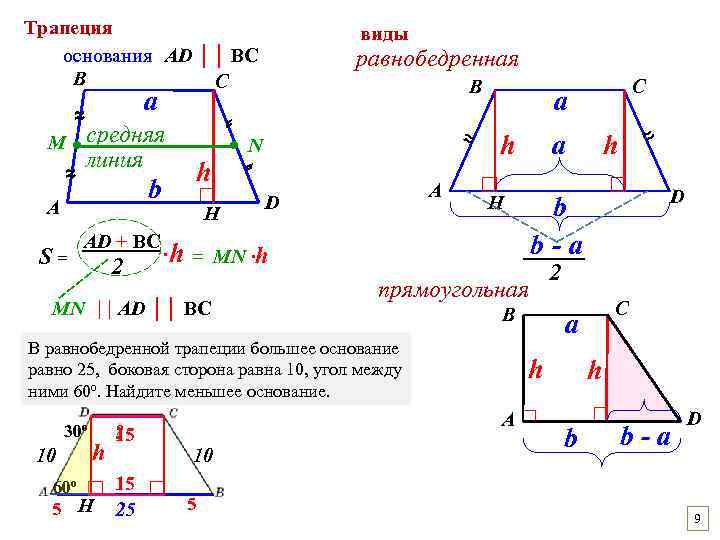
Трапеция основания АD ││ BC В С a ≈ M ● средняя линия ≈ S= АD + BC 2 равнобедренная В ⸗ □ H ∙h = MN ││ АD ││ BC ⸗ А D 30⁰ 10 h ? 15 □ 60⁰ 5 H 25 10 5 h a □ H прямоугольная В □ D 2 С a h А□ ≈ h b b-a MN ∙h В равнобедренной трапеции большее основание равно 25, боковая сторона равна 10, угол между ними 60⁰. Найдите меньшее основание. С a ≈ ● N h b А виды h b □ b-а D 9
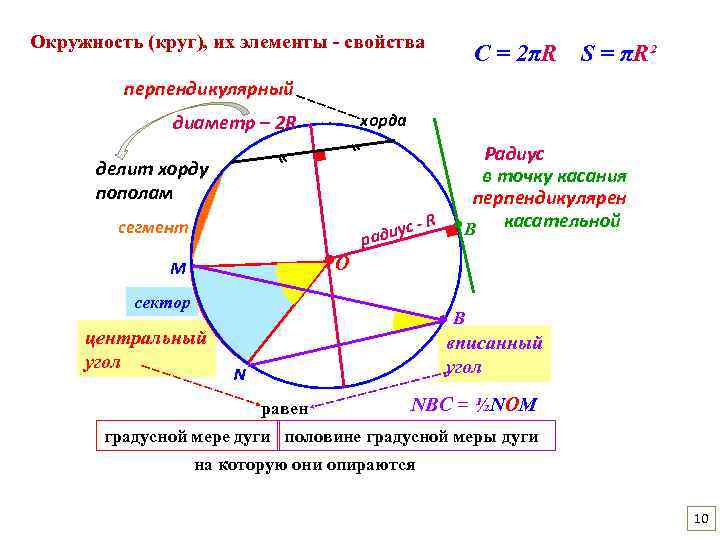
Окружность (круг), их элементы - свойства С = 2πR S = πR² перпендикулярный хорда диаметр – 2 R ▪ ⸗ Радиус в точку касания перпендикулярен касательной В ⸗ делит хорду пополам сектор В ● центральный угол R ● ●О M садиу р ▪ сегмент вписанный угол N равен NBC = ½NOM градусной мере дуги половине градусной меры дуги на которую они опираются 10
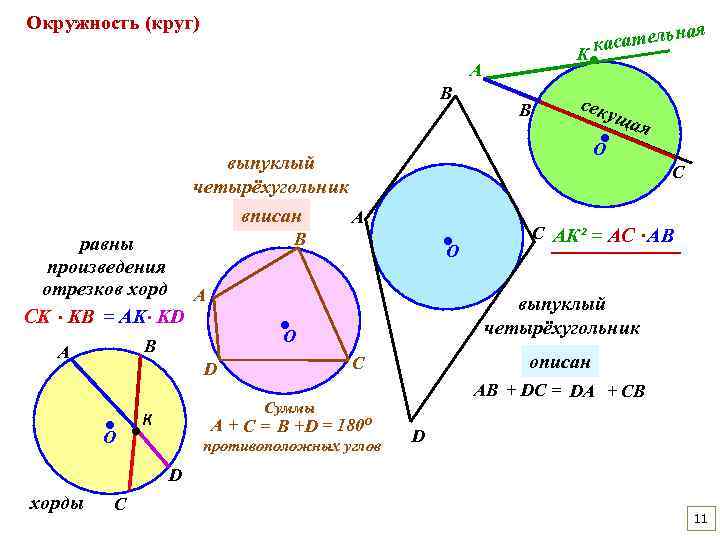
Окружность (круг) ная ь касател К ● А В ● О ● ● О С АК² = АС ∙ АВ описан С АВ + DC = DА + CB Суммы К я выпуклый четырёхугольник ● О D уща С В В А сек ● О выпуклый четырёхугольник вписан А равны произведения отрезков хорд А СK ∙ KB = AK ∙ KD В А + С = В +D = 180⁰ противоположных углов D D хорды С 11
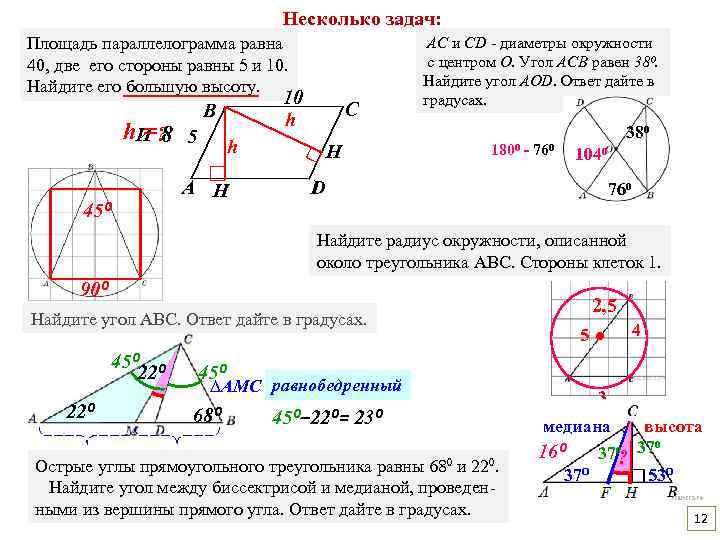
Несколько задач: Площадь параллелограмма равна 40, две его стороны равны 5 и 10. Найдите его большую высоту. h. И ? 5 =8 10 h В h □ А H 45⁰ С □H AC и CD - диаметры окружности с центром O. Угол ACB равен 38⁰. Найдите угол AOD. Ответ дайте в градусах. 180⁰ - 76⁰ 38⁰ 104⁰ D 76⁰ Найдите радиус окружности, описанной около треугольника АВС. Стороны клеток 1. 90⁰ Найдите угол АВС. Ответ дайте в градусах. 45⁰ 22⁰ 2, 5 5● 4 45⁰ ∆АМС равнобедренный 68⁰ 45⁰‒ 22⁰= 23⁰ Острые углы прямоугольного треугольника равны 680 и 220. Найдите угол между биссектрисой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах. 3 медиана высота 16⁰ 37⁰? 37⁰ 53⁰ 12
Геометрия - торетический курс 7-9..pptx