термодинамика.pptx
- Количество слайдов: 63


В любом живом организме осуществляются процессы обмена веществ, которые включают огромное количество непрерывно протекающих и взаимодействующих между собой реакций, в ходе которых выделяется или поглощается энергия. Этот процесс обмена веществ и энергии является самым характерным признаком жизни, т. к. с его прекращением прекращается и жизнь.
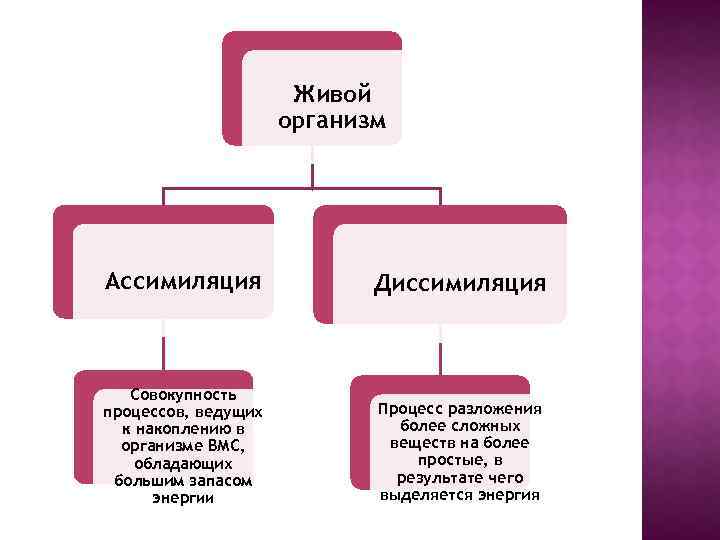
Живой организм Ассимиляция Диссимиляция Совокупность процессов, ведущих к накоплению в организме ВМС, обладающих большим запасом энергии Процесс разложения более сложных веществ на более простые, в результате чего выделяется энергия

С открытием закона сохранения и превращения энергии учение о взаимных переходах различных форм энергии выделилось из физики в самостоятельную науку термодинамику-науку о превращениях различных форм энергий и законах их превращений. Термодинамика изучает состояние и превращения, происходящие с макросистемами.

Химическая термодинамика изучает: Переход энергии из одной формы в другую, от одной части системы к другой; Энергитические эффекты, сопровождающие физические и химические процессы; Возможность и направленность самопроизвольных процессов.

Термодинамическая системалюбой макроскопический материальный объект, отделённый от внешней среды реальной или воображаемой границей. Объекты природы, не входящие в систему, называются средой.

1. Изолированные-(Δ m=0; Δ Е=0) 2. Закрытые-(Δ m=0; Δ Е≠ 0) 3. Открытые-(Δ m≠ 0; Δ Е≠ 0).

2. 1. 3.

1. Гомогенные- отсутствуют резкие изменения физических и химических свойств при переходе от одних областей системы к другим, следовательно, не существует поверхности раздела между отдельными частями системы. 2. Гетерогенные- состоят из двух или более гомогенных систем. Такие системы состоят из отдельных частей (фаз), имеющих поверхность раздела.

1. 2.

Фаза-совокупность частей системы, схожих по химическому составу и термодинамическим свойствам и находящимся между собой в термодинамическом равновесии. Гомогенная система- однофазна; Гетерогенная система состоит из двух или более фаз.

Компонентами равновесной системы называются её независимые составные части, минимальным числом которых может быть выражен состав любой из фаз. Каждый компонентиндивидуальное химическое вещество, которое может быть выделено из системы и существовать в изолированном виде.

Пример: раствор Na. Cl содержит частицы: Молекулы Na. Cl Молекулы воды Ионы Na+, ионы Cl-, в небольшом количестве ионы Н+ и ОНКакой тип системы представлен?

Раствор Na. Cl- система: Гомогенная Однофазная Двухкомпонентная( Н 2 О и Na. Cl). Состояние системы можно описать с помощью термодинамических переменных-параметров системы.

Интенсивные- не зависят от массы системы (t, Р); Экстенсивные- пропорциональны массе и количеству вещества в системе(V, U, S). Внешние- не связаны с процессами, происходящими внутри (Р, t); Внутренние- определяют внутреннее состояние системы(энергия связей, энергия вращательного, колебательного движения молекул , атомов и др. )

- совокупность свойств системы, позволяющих определить систему с точки зрения термодинамики. Равновесное- такое состояние, при котором все свойства системы остаются постоянными в течение большого промежутка времени и в системе отсутствуют потоки веществ и энергии; Стационарное- состояние системы, при котором свойства системы постоянны во времени, но имеются потоки вещества и энергии;

Переходное- свойства системы изменяются во времени. Переход системы из одного состояния в другое называется процессом.

Изотермические (Δ Т=0) Изобарные (Δ Р=0) Изохорные (Δ V=0) Адиабатные (Δ Q=0).

Первое начало термодинамики устанавливает соотношение между теплотой Q, работой А и изменением внутренней энергии системы ΔU: Изменение внутренней энергии системы равно количеству сообщенной системе теплоты минус количество работы, совершенной системой против внешних сил. ΔU = Q - А (I. 1) d. U=d. Q-A (I. 2) Уравнение (I. 1) является математической записью 1 -го начала термодинамики для конечного, уравнение (I. 2) – для бесконечно малого изменения состояния системы.

Внутренняя энергия является функцией состояния; это означает, что изменение внутренней энергии ΔU не зависит от пути перехода системы из состояния 1 в состояние 2 и равно разности величин внутренней энергии U 2 и U 1 в этих состояниях: ΔU = U 2 - U 1 (I. 3) Следует отметить, что определить абсолютное значение внутренней энергии системы невозможно; термодинамику интересует лишь изменение внутренней энергии в ходе какого-либо процесса.

Энергия – мера способности системы совершать работу; общая качественная мера движения и взаимодействия материи. Энергия является неотъемлемым свойством материи. Различают потенциальную энергию, обусловленную положением тела в поле некоторых сил, и кинетическую энергию, обусловленную изменением положения тела в пространстве. Внутренняя энергия системы – сумма кинетической и потенциальной энергии всех частиц, составляющих систему. Можно также определить внутреннюю энергию системы как её полную энергию за вычетом кинетической и потенциальной энергии системы как целого.

Формы перехода энергии от одной системы к другой могут быть разбиты на две группы. В первую группу входит только одна форма перехода движения путем хаотических столкновений молекул двух соприкасающихся тел, т. е. путём теплопроводности (и одновременно путём излучения). Мерой передаваемого таким способом движения является теплота. Теплота есть форма передачи энергии путём неупорядоченного движения молекул.

Во вторую группу включаются различные формы перехода движения, общей чертой которых является перемещение масс, охватывающих очень большие числа молекул (т. е. макроскопических масс), под действием каких-либо сил. Таковы поднятие тел в поле тяготения, переход некоторого количества электричества от большего электростатического потенциала к меньшему, расширение газа, находящегося под давлением и др. Общей мерой передаваемого такими способами движения является работа – форма передачи энергии путём упорядоченного движения частиц.

Теплота и работа характеризуют качественно и количественно две различные формы передачи движения от данной части материального мира к другой. Теплота и работа не могут содержаться в теле. Теплота и работа возникают только тогда, когда возникает процесс, и характеризуют только процесс. В статических условиях теплота и работа не существуют. Различие между теплотой и работой, принимаемое термодинамикой как исходное положение, и противопоставление теплоты работе имеет смысл только для тел, состоящих из множества молекул, т. к. для одной молекулы или для совокупности немногих молекул понятия теплоты и работы теряет смысл.

В биологических системах теплота обычно отдаётся системой во внешнюю среду, а работа совершается системой за счёт убыли внутренней энергии. В условиях живого организма выделяют несколько видов работ: Химическая- работа, совершаемая при синтезе различных ВМС из НМС в результате химических реакций;

Механическая- работа по перемещению частей и органов тела против механических сил (совершается мышцами при сокращении); Осмотическая- работа по переносу различных веществ через мембраны из области с более низкой концентрацией веществ в область с более высокой их концентрацией;

Электрическая- работа по переносу заряженных частиц в электрическом поле(совершается при передаче нервного возбуждения по клеткам); Работа по высвечиваниюизлучение органами животных сверхслабого электромагнитного излучения

Изохорные процессы: Q= Δ U+A A=P ΔV; ΔV=0 Q= ΔU В условиях изохорного процесса вся теплота, подведённая к системе, расходуется на изменение внутренней энергии.

Q= Δ U+A ΔU = U 2 - U 1 A=PΔV = P( V 2 -V 1) Q=(U 2 - U 1 ) - P( V 2 -V 1)= =(U 2+ P∙V 2 ) –(U 1 + P∙V 1)= =H 2 - H 1 = Δ H В условиях изобарного процесса теплота, подведённая к системе, расходуется на изменение энтальпии(энергосодержания).

Химические реакции протекании которых происходит уменьшение энтальпии и во внешнюю среду выделяется теплота, называются экзотермическими. Реакции, в результате которых энтальпия возрастает и система поглощает теплоту извне, называются эндотермическими. В термодинамике принято считать тепло, поглощённое системой(эндотермические реакции), положительным, а тепло, отданное системой(экзотермические реакции)отрицательным.

Экзотермическая реакция экзотермическая реакция

Термохимические уравнения: Указан тепловой эффект реакции(Δ Н); Указано агрегатное состояние исходных веществ и продуктов реакции: Н 2(Г) + 1/2 О 2(Г) = Н 2 О(ж); ΔН=-286 кдж/моль Закон Гесса(1940 г. ): тепловой эффект реакции зависит от вида и состояния исходных веществ и продуктов реакции и не зависит от пути перехода( V- const, P-const, t-const)

Г. И. Гесс известен как один из основоположников термохимии. В 1840 открыл закон постоянства сумм тепла (Закон Гесса). 1802 -1850 г
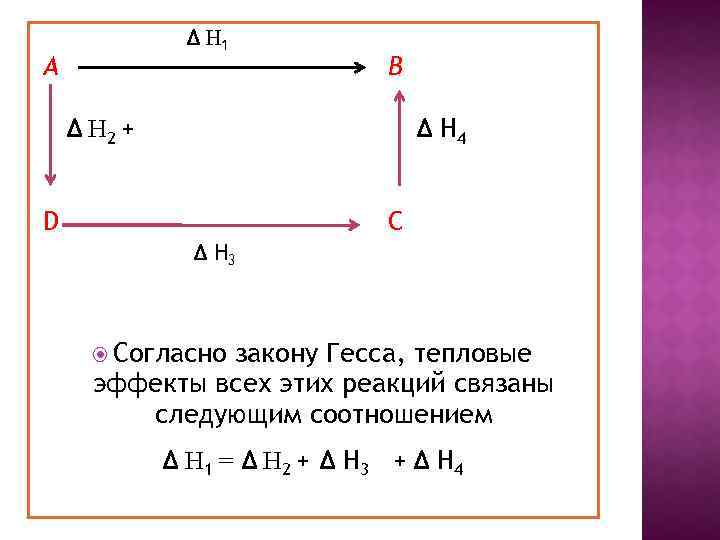
Δ Н 1 А В Δ Н 2 + Δ Н 4 D C Δ Н 3 Согласно закону Гесса, тепловые эффекты всех этих реакций связаны следующим соотношением Δ Н 1 = Δ Н 2 + Δ Н 3 + Δ Н 4

Например: С + О 2 = СО 2 ; Δ Н 1 = - 394 кдж/моль С + 1/2 О 2 = СО; Δ Н 2 = -110 кдж/моль СО +1/2 О 2 = СО 2 ; Δ Н 3 = -283 кдж/моль Δ Н 1 = Δ Н 2 + Δ Н 3 = - 394 кдж/моль

1 следствие: тепловой эффект реакции (стандартная энтальпия) равен сумме теплот образования(стандартных энтальпий образования) стехиометрического количества продуктов реакции за вычетом суммы теплот образования(стандартных энтальпий образования) стехиометрического количества исходных веществ. 2 следствие: тепловой эффект реакции (стандартная энтальпия) равен сумме теплот сгорания(стандартных энтальпий сгорания) стехиометрического количества исходных веществ за вычетом суммы теплот сгорания(стандартных энтальпий сгорания) стехиометрического количества продуктов реакции.

Δ Н(х. р. ) = ∑Δ Н обр. (прод. р. ) - ∑ ΔН обр. (исх. в. ) Δ Н(х. р. ) = ∑ ΔН сгор. (исх. в. ) - ∑ ΔН –сгор. (прод. р. ) Энтальпия образования –тепловой эффект реакции образования 1 моль сложного вещества из простых веществ. Энтальпия сгорания-тепловой эффект сгорания 1 моль сложного вещества до простейших оксидов.

Величины тепловых эффектов химических реакций зависят от условий, в которых проводятся реакции. Поэтому табличные значения теплот различных процессов принято относить к стандартному состоянию – температуре 298 К и давлению 101325 Па (760 мм. рт. ст. ; 1 атм. ); величины тепловых эффектов при данных условиях называют стандартными тепловыми эффектами и обозначают ΔН° 298 и ΔU° 298 соответственно.

Первое начало термодинамики утверждает, что при превращении одной формы энергии в другую полная энергия системы не изменяется, однако не указывает никаких ограничений относительно возможности этого процесса. Поэтому первое начало термодинамики позволяет рассчитать энергетический эффект процесса, однако не дает ответа на вопросы о том, будет ли процесс протекать самопроизвольно, о направлении и глубине протекания процесса. Самопроизвольный процесс – процесс, который может протекать без затраты работы извне, причем в результате может быть получена работа в количестве, пропорциональном произошедшему изменению состояния системы

Второе начало термодинамики дает возможность определить, какой из процессов будет протекать самопроизвольно, какое количество работы может быть при этом получено, каков предел самопроизвольного течения процесса второе начало термодинамики дает возможность определить, какими должны быть условия, чтобы нужный процесс протекал в необходимом направлении и в требуемой степени, что особенно важно для решения различных задач прикладного характера.

Попыткой воспользоваться 1 началом термодинамики для оценки направления химической реакции явился принцип Бертло-Томсена , согласно которому, самопроизвольно протекают лишь те процессы, которые сопровождаются выделением теплоты (уменьшением энтальпии). Однако известны процессы, в результате протекания которых энтальпия системы либо не изменяется, либо возрастает(например, растворение в воде солей аммония)

Для прогнозирования возможности и направленности самопроизвольного процесса, необходимо ввести ещё одну функцию состояния системы, которая не зависит от пути реализации процесса и изменение этой функции должно иметь один и тот же знак; Если рассмотреть любой самопроизвольный процесс, то можно отметить, что в ходе его реализации всегда происходит увеличение беспорядка в системе.
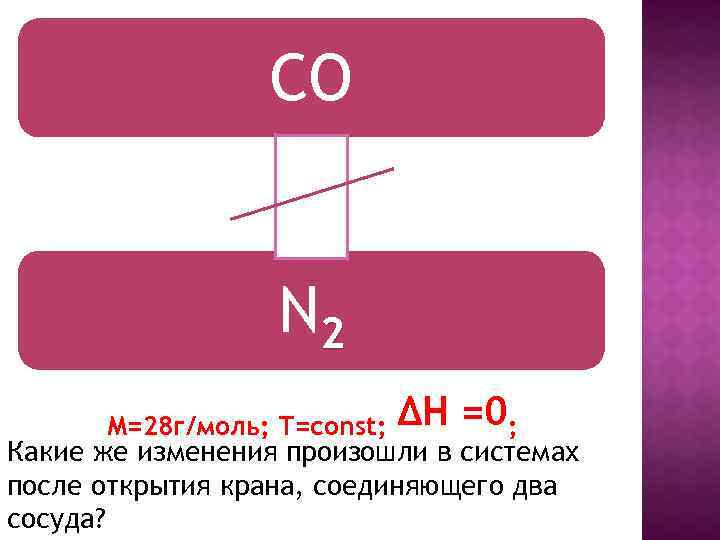
СO N 2 М=28 г/моль; Т=соnst; ΔН =0; Какие же изменения произошли в системах после открытия крана, соединяющего два сосуда?

Все параметры системы остались постоянными, кроме степени беспорядка в системе. Мерой этой неупорядоченности является функция состояния системы, называемая энтропией (S) Классическая термодинамика рассматривает происходящие процессы безотносительно к внутреннему строению системы; поэтому в рамках классической термодинамики показать физический смысл энтропии невозможно. Для решения этой проблемы Больцманом в теорию теплоты были введены статистические представления. Каждому состоянию системы приписывается термодинамическая вероятность (определяемая как число микросостояний, составляющих данное макросостояние системы), тем большая, чем более неупорядоченным или неопределенным является это состояние.

Т. о. , энтропия есть функция состояния, описывающая степень неупорядоченности системы. Количественная связь между энтропией S и термодинамической вероятностью W выражается формулой Больцмана: S= klg. W, k-постоянная Больцмана С точки зрения статистической термодинамики второе начало термодинамики можно сформулировать следующим образом: Система стремится самопроизвольно перейти в состояние с максимальной термодинамической вероятностью.

В то же время второе начало термодинамики имеет ограниченную область применения: оно применимо лишь к макроскопическим системам. некоторые формулировки второго начала термодинамики: Теплота не может самопроизвольно переходить от менее нагретого тела к более нагретому (постулат Клаузиуса). Невозможен процесс, единственным результатом которого является превращение теплоты в работу. Невозможно построить машину, все действия которой сводились бы к производству работы за счет охлаждения теплового источника (вечный двигатель второго рода).

СМЫСЛ ТЕРМОДИНАМИЧЕСКОЙ ВЕРОЯТНОСТИ Допустим в сосуде, мысленно разделенном на две половины, находится 4 невзаимодействующих молекулы. Каковы их возможные способы распределения по двум половинам?
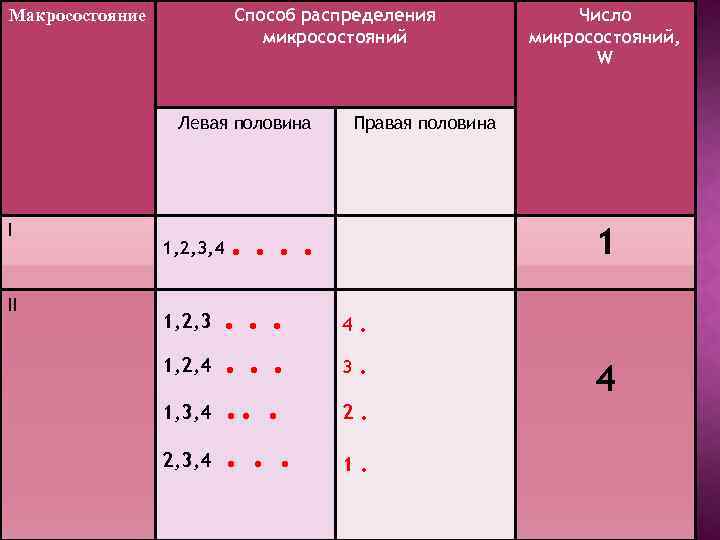
Способ распределения микросостояний Макросостояние Левая половина I II 1, 2, 3, 4 1, 2, 3 1, 2, 4 1, 3, 4 2, 3, 4 Правая половина . . . . Число микросостояний, W 1 4 . 3 . 2 . 1 . 4
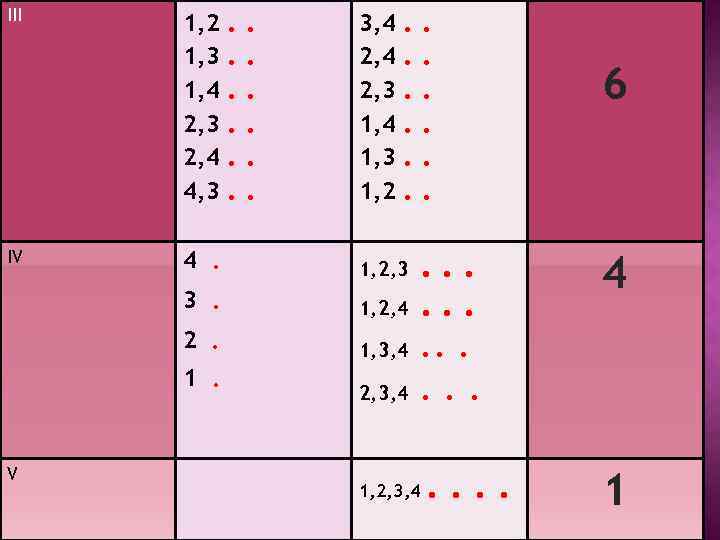
III IV 1, 2 1, 3 1, 4 2, 3 2, 4 4, 3 . . . 3, 4 2, 3 1, 4 1, 3 1, 2 . . . 4. 1, 2, 3 3. 1, 2, 4 2. 1, 3, 4 1. V 2, 3, 4 . . . 6 4 . . . 1, 2, 3, 4 . . 1

В Чем большим числом микросостояний характеризуется данное макросостояние, тем больше различных вероятностей равномерного распределения приведённом примере термодинамическая вероятность наибольшая для распределения 3, которое характеризуется равномерным распределением молекул.

Закономерности изменения энтропии: энтропия возрастает: при переходе от твёрдых веществ к жидкостям и газам; при переходе из более твёрдого состояния в менее твёрдое; при увеличении числа атомов в молекуле(О 2 и О 3); в гомологическом ряду с увеличением числа атомов углерода; в химических реакциях, сопровождающихся увеличением количества(моль) газообразных веществ.

Энтропия уменьшается при: Отвердевании Охлаждении Кристаллизации Уменьшении количества(моль) газообразных веществ в химических реакциях.

Исходя из нового понятия энтропии, можно дать ещё одну формулировку 2 начала термодинамики, согласно которому всякий самопроизвольный процесс в изолированной системе идёт с возрастанием энтропии. В обратимом процессе изменение энтропии не происходит, Δ S=0. Возникает вопрос: можно ли обратить самопроизвольный процесс? Второй закон термодинамики отвечает, что это возможно, но при условии создания эквивалентной или ещё большей микроскопической неупорядоченности где-то в другом месте.

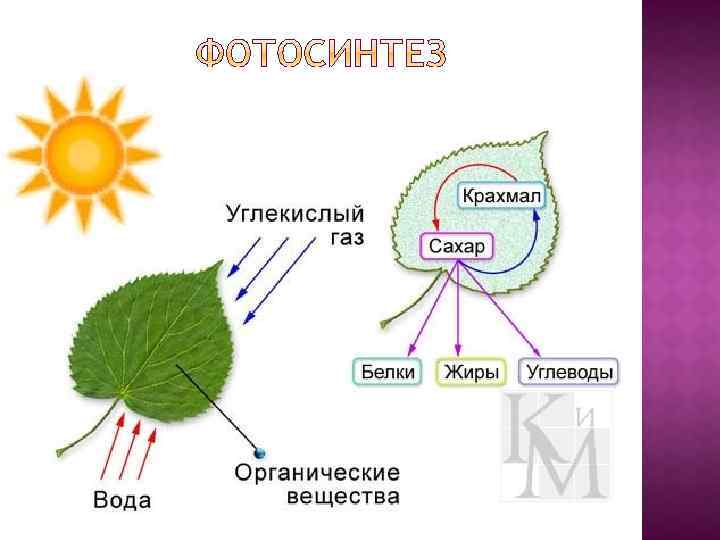
Примером может служить процесс фотосинтеза, при котором СО 2 , Н 2 О и др. питательные вещества поглощаются растениями и за их счёт синтезируются ВМС(углеводы). Этот процесс сопровождается понижением энтропии. Чтобы происходил процесс фотосинтеза, растениям необходима солнечная энергия. Поэтому уменьшение энтропии при переходе от СО 2 и Н 2 О к углеводам компенсируется возрастанием энтропии на солнце.

Многие другие фундаментальные биохимические процессы осуществляются с уменьшением энтропии, например, активный транспорт ионов через клеточную мембрану и др. , что, на первый взгляд, противоречит термодинамическим закономерностям. Живой организм- открытая система, в которой энтропия может возрастать, оставаться постоянной или даже уменьшаться

Примером может служить Вселенная. Если считать Вселенную изолированной системой, то все события в ней должны приводить к увеличению энтропии, в конечном итоге должно быть достигнуто состояние маx энтропии, после чего уже невозможны никакие события, а это состояние известно как «тепловая смерть Вселенной» . Однако, оно никогда не будет достигнуто, т. к. Вселенная не статична и непрерывно эволюционирует.

В то время как абсолютное значение энтальпии определить невозможно и вычисляется только её изменение, вычисление абсолютного значения энтропии- вполне возможная задача. Абсолютное значение энтропии используют для вычисления стандартных энтропий веществ, которая равна разности между суммами абсолютных энтропий продуктов реакции и абсолютных энтропий исходных веществ: Δ S = S (прод. р. )- S (исх. в. )

Итак, имеется два стимула для самопроизвольно протекающих процессов: снижение суммарной энергии системы(уменьшение энтальпии); более равномерное распределение энергии по компонентам и пространству системы( увеличение энтропии). Для изолированных и закрытых систем Δ S и Δ H могут являться критериями направленности самопроизвольных процессов.

Для открытых систем важна результирующая этих термодинамических величин. Результирующий критерий, определяющий возможность процесса, есть баланс действия этих двух стимулов

Для открытых систем показателем возможности самопроизвольного процесса является функция состояния системысвободная энергия Гиббса, изменение которой может быть рассчитано по формуле: ΔG = Δ H – T ΔS По знаку ΔG судят о возможности протекания самопроизвольных процессов:

1. ΔG 0 -процесс возможен; 2. ΔG 0 - процесс невозможен; 3. ΔG=0 -система находится в состоянии равновесия Знак ΔG зависит от соотношения Δ H и T ΔS: Если реакция экзотермическая (Δ H<0), а ΔS положительна, то при любой температуре процесс будет идти самопроизвольно; Т. к. ΔG-функция состояния системы, для её вычисления можно использовать первое следствие из закона Гесса: ΔG(хим. р. )= ΔG(прод. р)- ΔG (исх. в. )

Итак, законы классической термодинамики могут быть использованы только для изолированных равновесных систем, а в живой природе таких систем нет. По этим причинам при термодинамическом подходе к биохимическим системам следует соблюдать осторожность в окончательных выводах. В то же время этот подход плодотворен при изучении химических процессов в неживой природе.
термодинамика.pptx