Скачать презентацию В — к п коэффициент пропорциональности Скачать презентацию В — к п коэффициент пропорциональности

63_BashykEvg_treyg.ppt

  • Количество слайдов: 12

= = В - к. п. (коэффициент пропорциональности) Отрезки АВ и СД- пропорциональны отрезкам = = В - к. п. (коэффициент пропорциональности) Отрезки АВ и СД- пропорциональны отрезкам А 1 В 1 и С 1 Д 1 подобен С А В 1 (коэффицие нт подобия) А 1 С 1

Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого.

Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия = Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия =

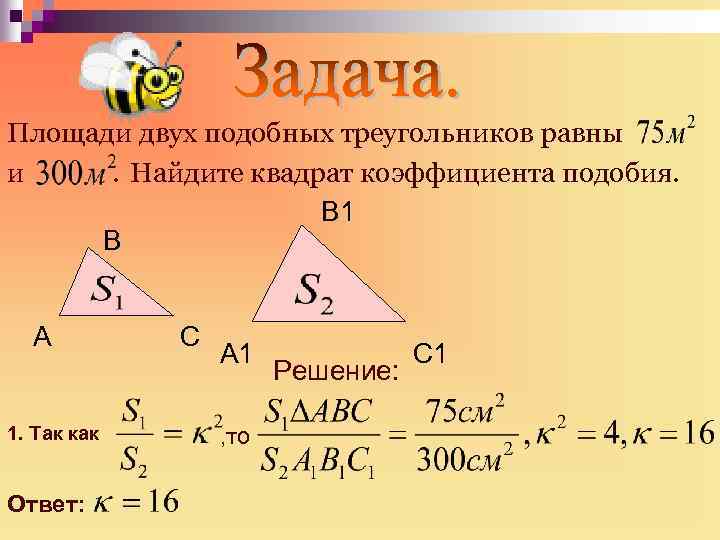Площади двух подобных треугольников равны и. Найдите квадрат коэффициента подобия. В 1 В А Площади двух подобных треугольников равны и. Найдите квадрат коэффициента подобия. В 1 В А 1. Так как Ответ: С А 1 , то Решение: С 1

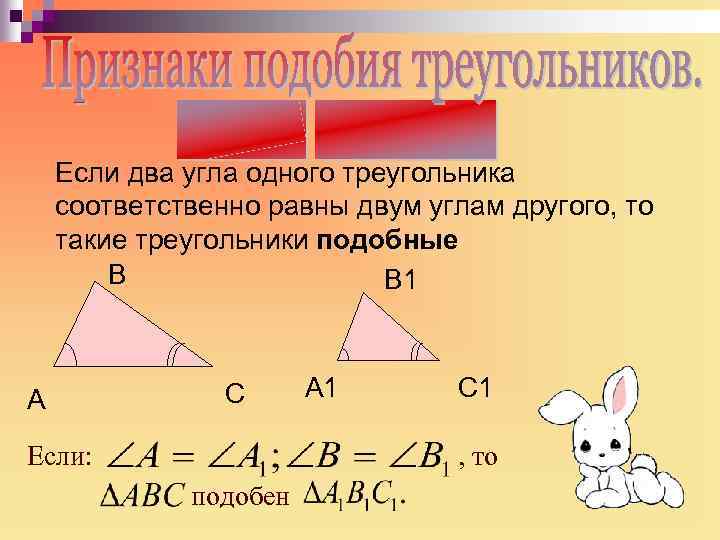Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобные Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобные В В 1 А С Если: А 1 С 1 , то подобен

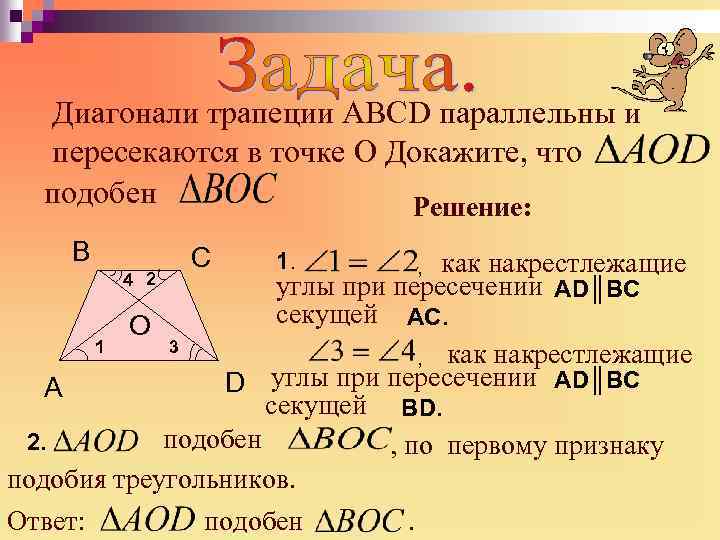Диагонали трапеции АВСD параллельны и пересекаются в точке О Докажите, что подобен Решение: B Диагонали трапеции АВСD параллельны и пересекаются в точке О Докажите, что подобен Решение: B C 1. как накрестлежащие углы при пересечении АD║ВС секущей АС. О 1 3 , как накрестлежащие D углы при пересечении АD║ВС A секущей ВD. подобен 2. , по первому признаку подобия треугольников. Ответ: подобен. 4 2 ,

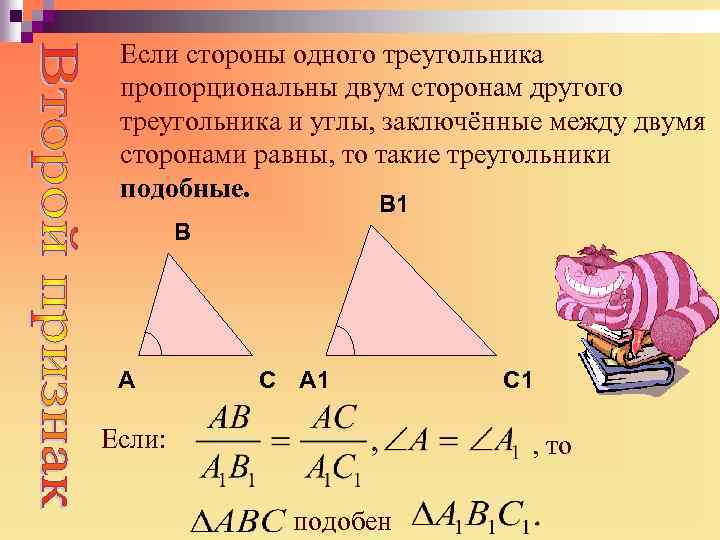Если стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключённые между двумя Если стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключённые между двумя сторонами равны, то такие треугольники подобные. В 1 В А С А 1 Если: С 1 , то подобен

Стороны треугольника стороны треугольника. Докажите, что B равны 5 см и 8 см. , Стороны треугольника стороны треугольника. Докажите, что B равны 5 см и 8 см. , а равны 10 см и 16 см, подобен. Решение: 1. A B 1 C подобен , по второму признаку подобия треугольников. подобен C 1 Ответ: 2. A 1

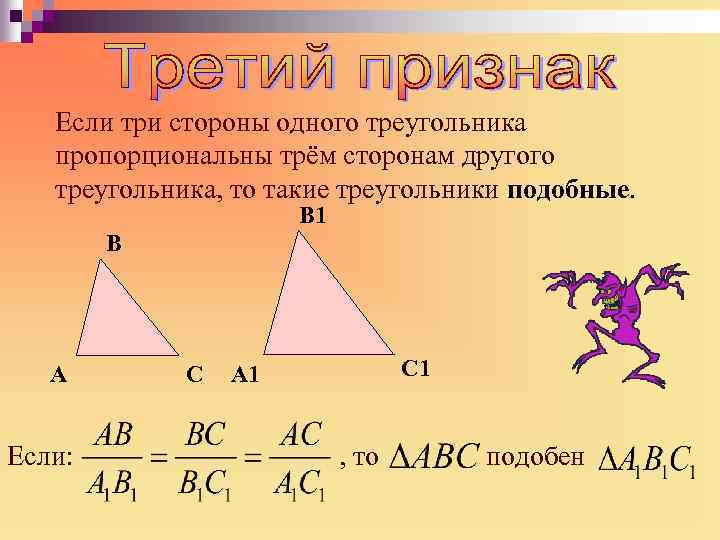Если три стороны одного треугольника пропорциональны трём сторонам другого треугольника, то такие треугольники подобные. Если три стороны одного треугольника пропорциональны трём сторонам другого треугольника, то такие треугольники подобные. B 1 B A Если: C C 1 A 1 , то подобен

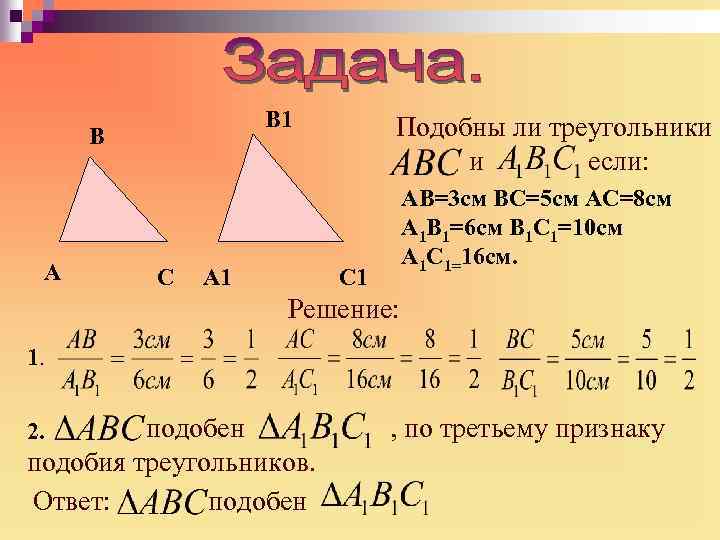B 1 B A C Подобны ли треугольники и если: АВ=3 см ВС=5 см B 1 B A C Подобны ли треугольники и если: АВ=3 см ВС=5 см АС=8 см А 1 В 1=6 см В 1 С 1=10 см А 1 С 1=16 см. C 1 A 1 Решение: 1. подобен подобия треугольников. Ответ: подобен 2. , по третьему признаку

1. Дайте определение подобных треугольников. 2. Сформулируйте теорему об отношении площадей подобных треугольников. 3. 1. Дайте определение подобных треугольников. 2. Сформулируйте теорему об отношении площадей подобных треугольников. 3. Сформулируйте теорему, выражающую первый признак подобия треугольников. 4. Сформулируйте теорему, выражающую второй признак подобия треугольников. 5. Сформулируйте теорему, выражающую третий признак подобия треугольников.