В е к т о р ы. О









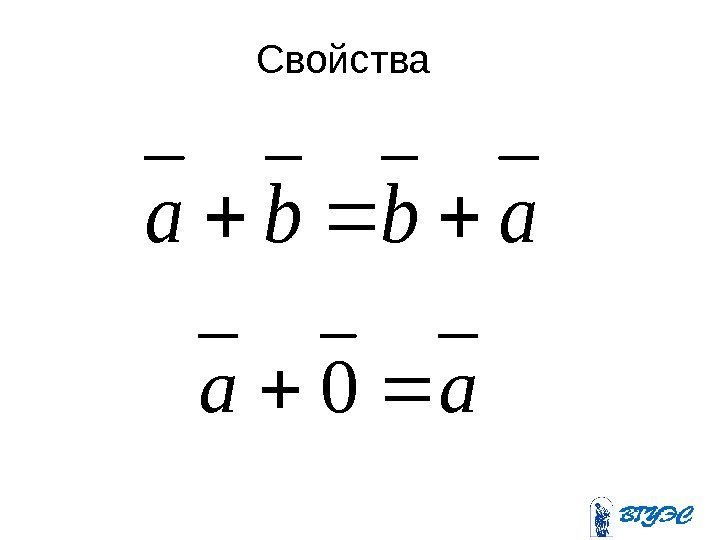
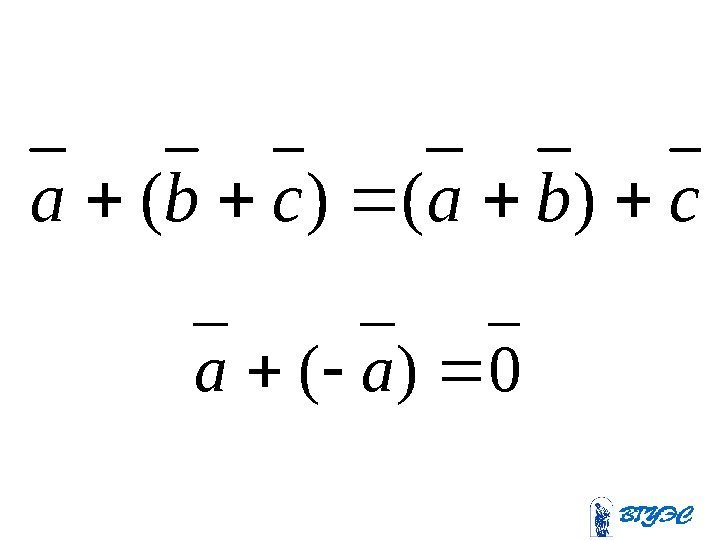

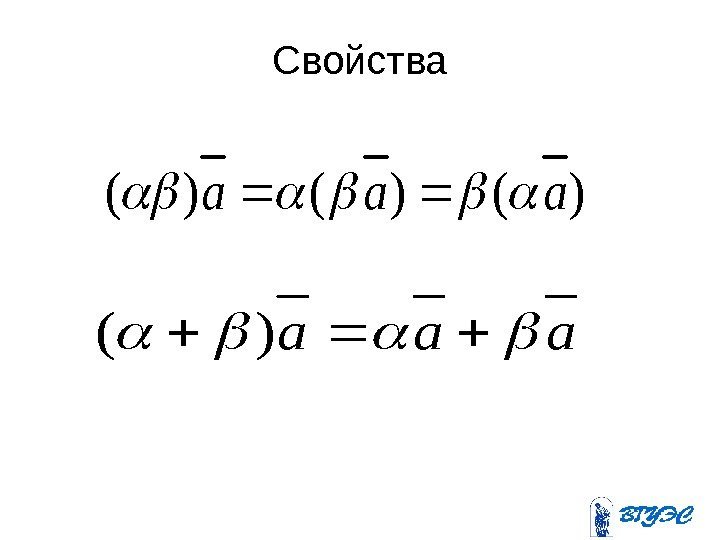
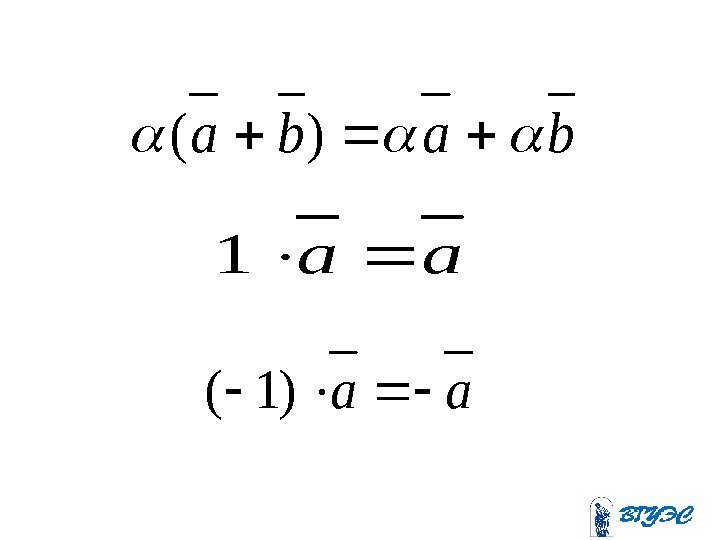

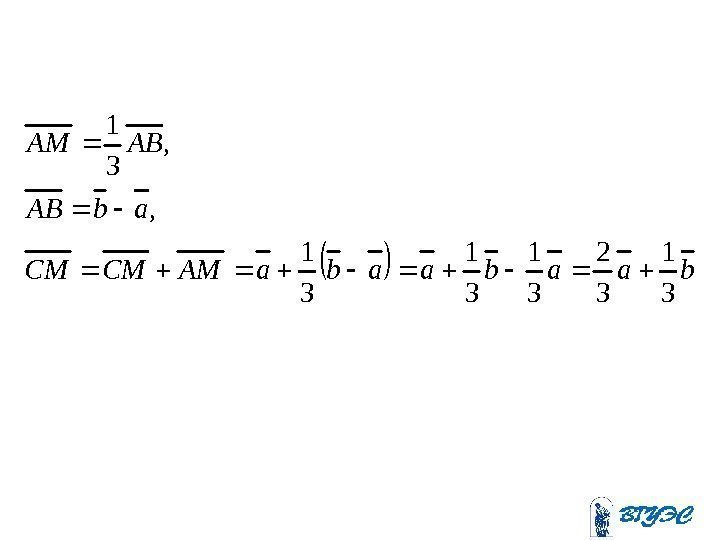






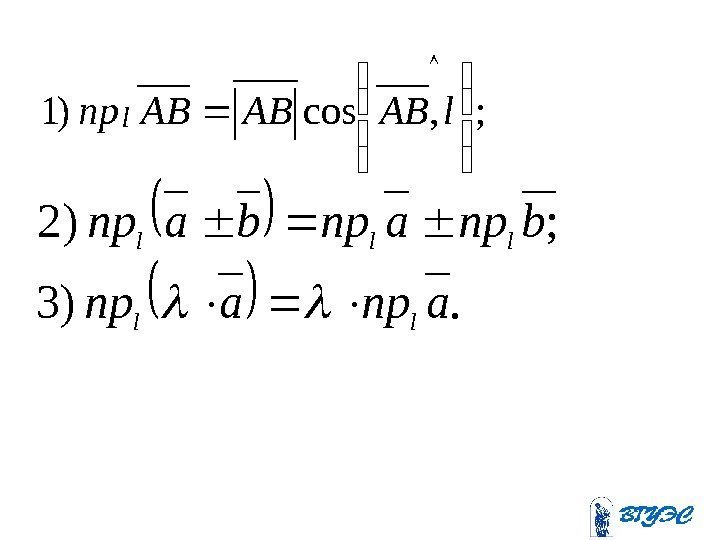





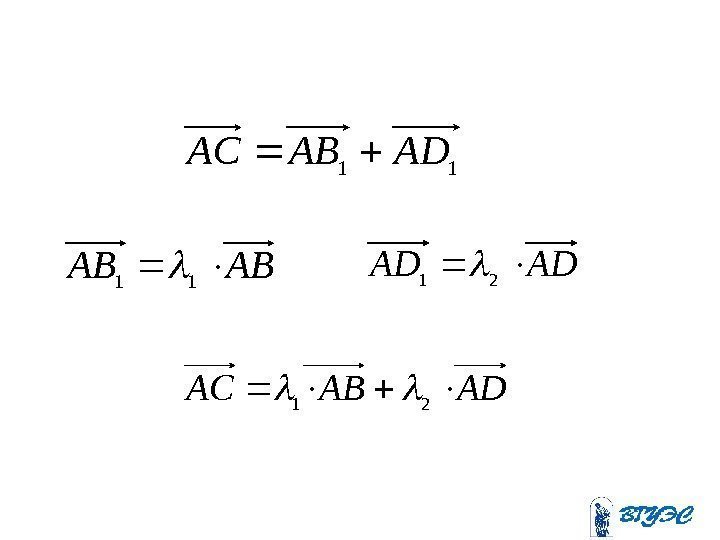






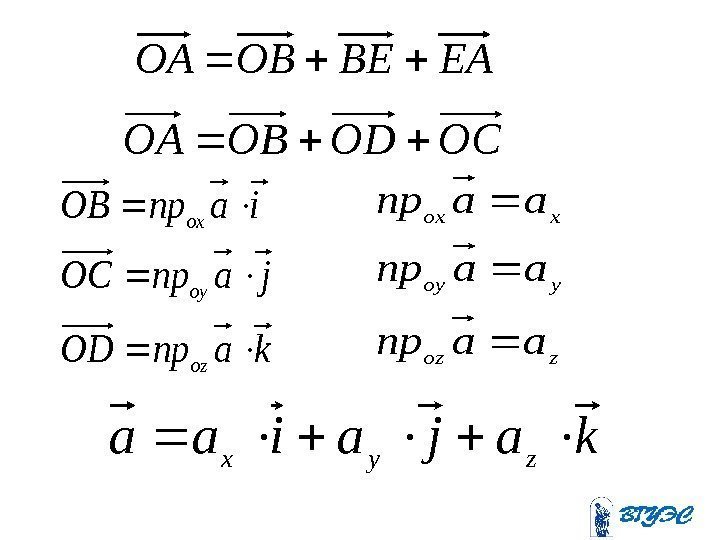

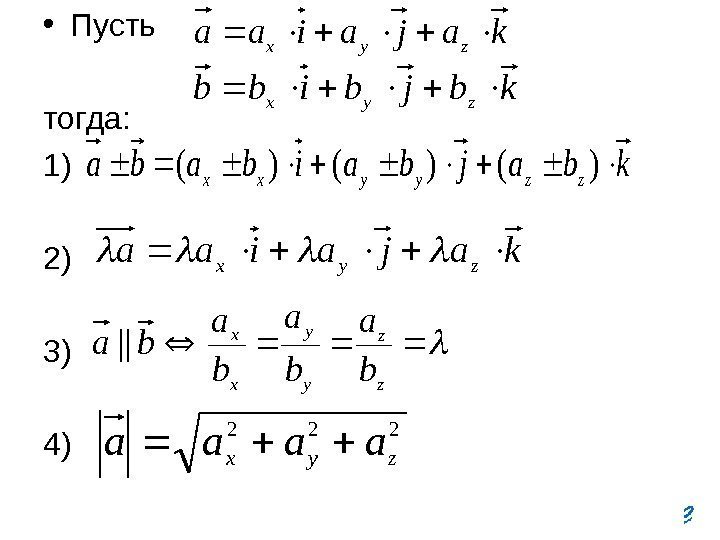
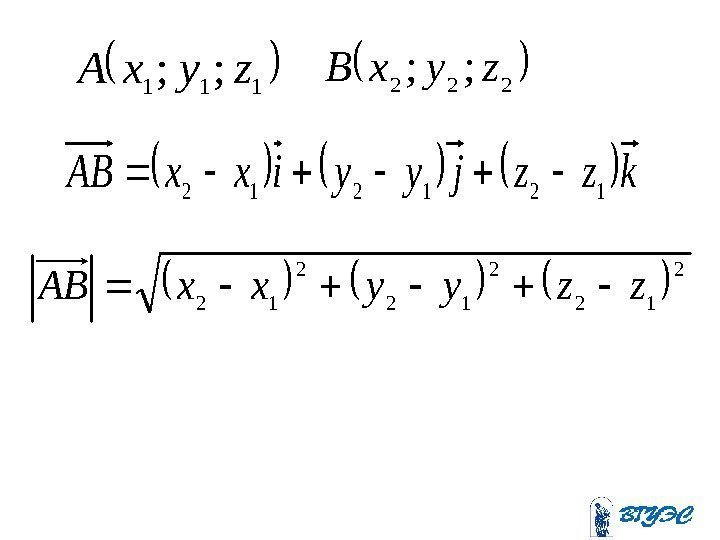

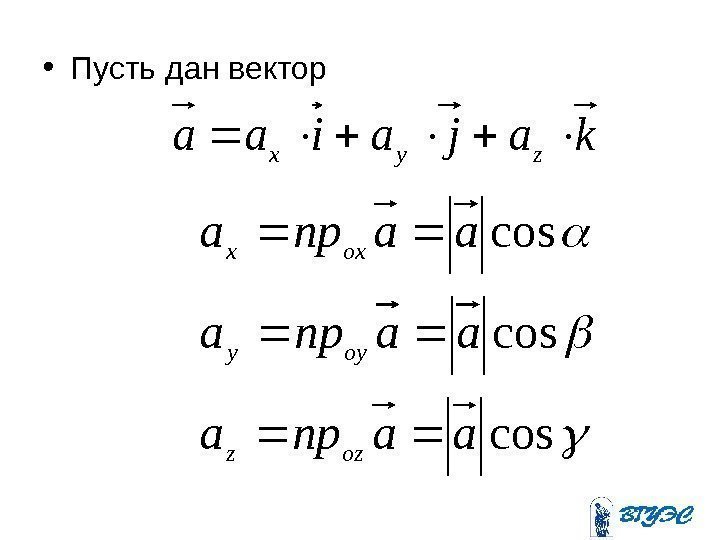
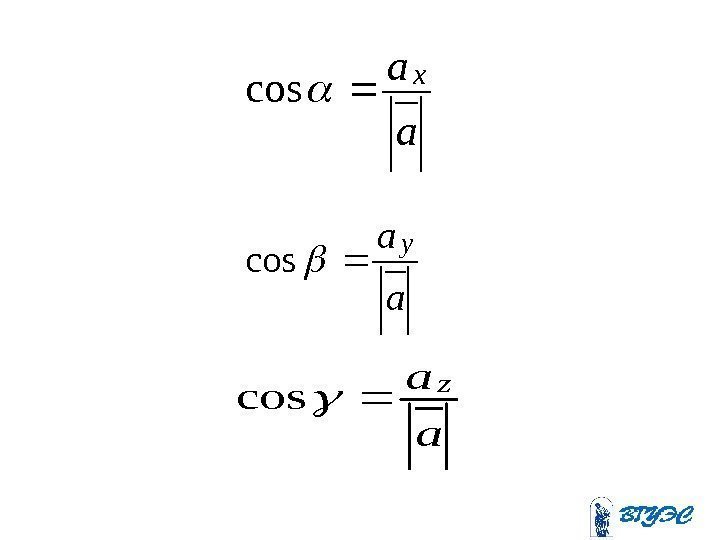
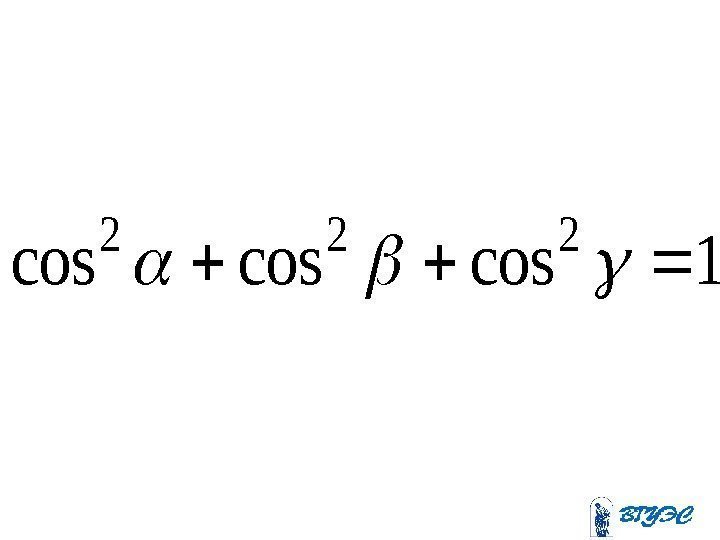



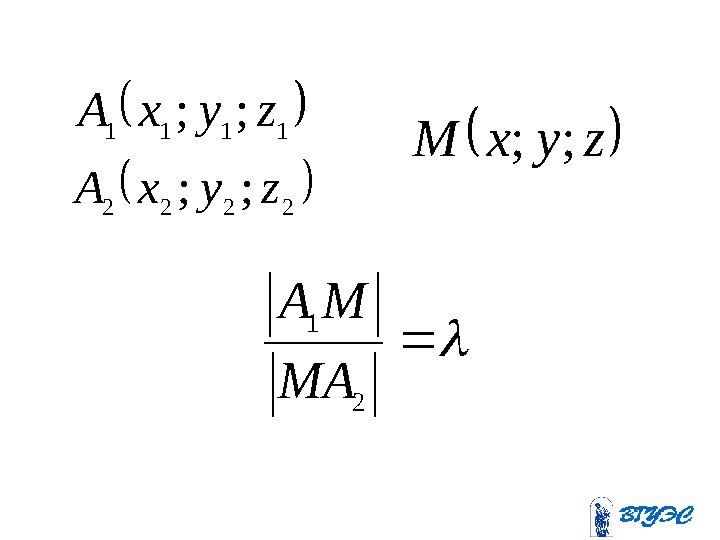
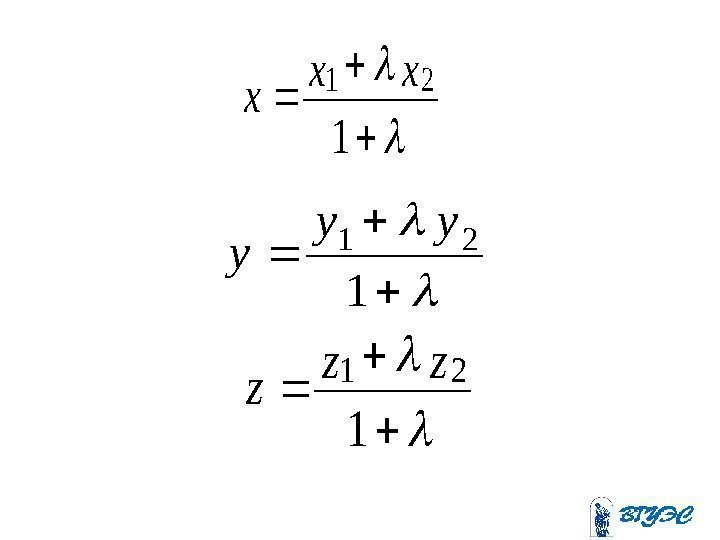
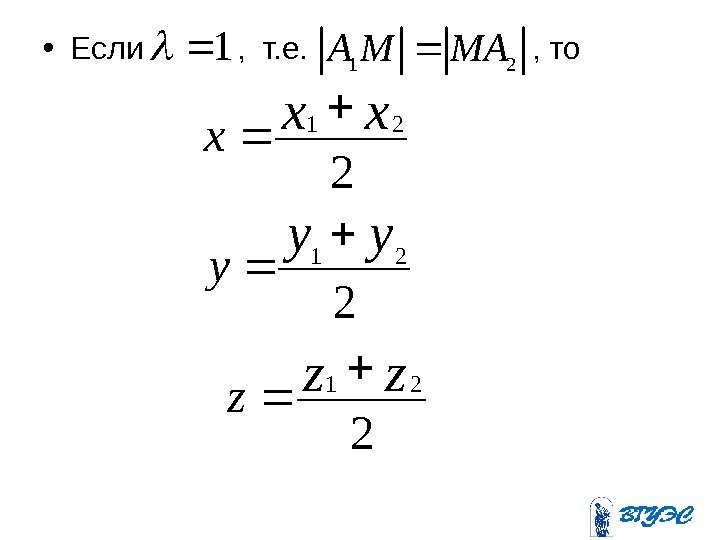

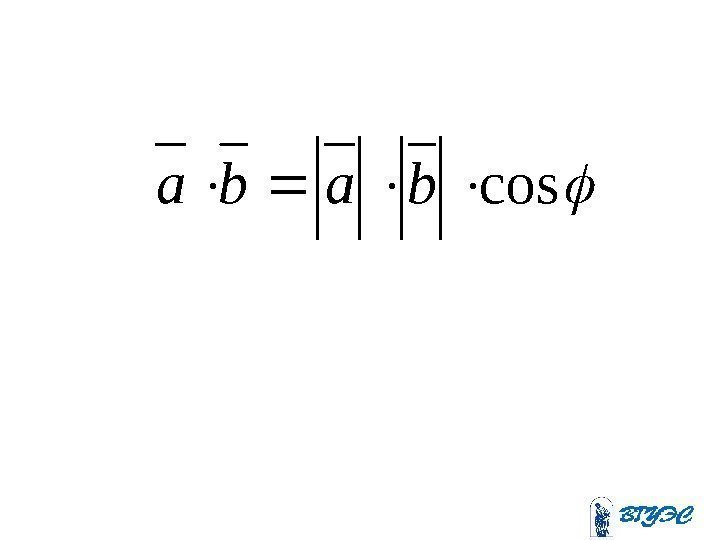

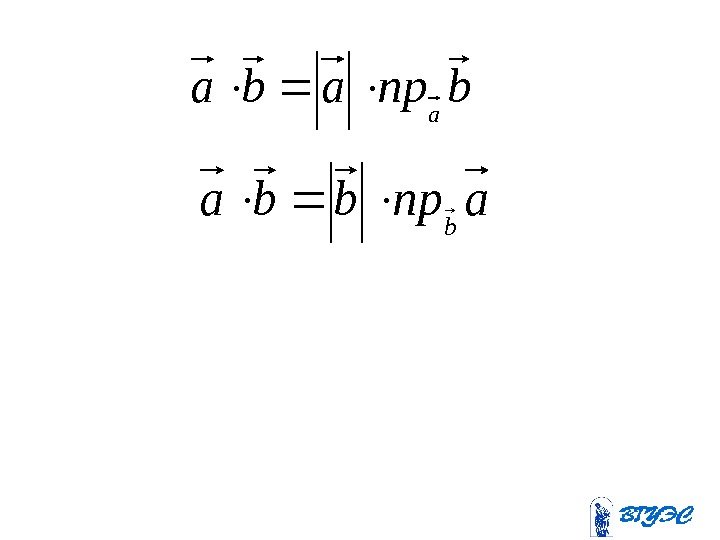
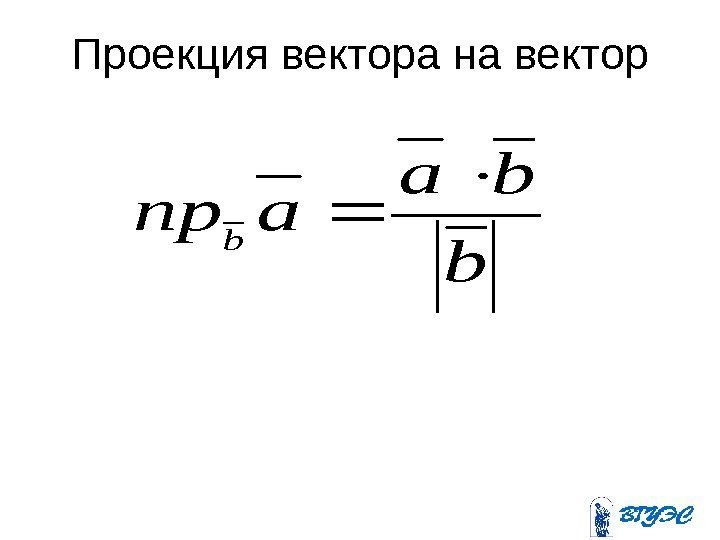




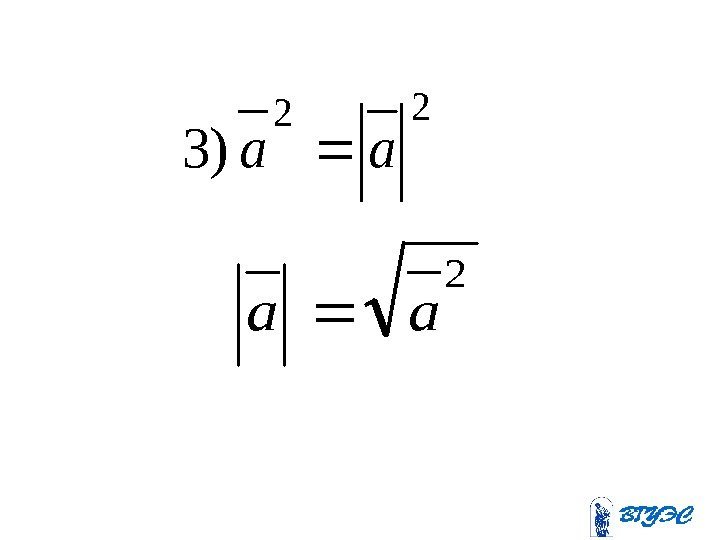



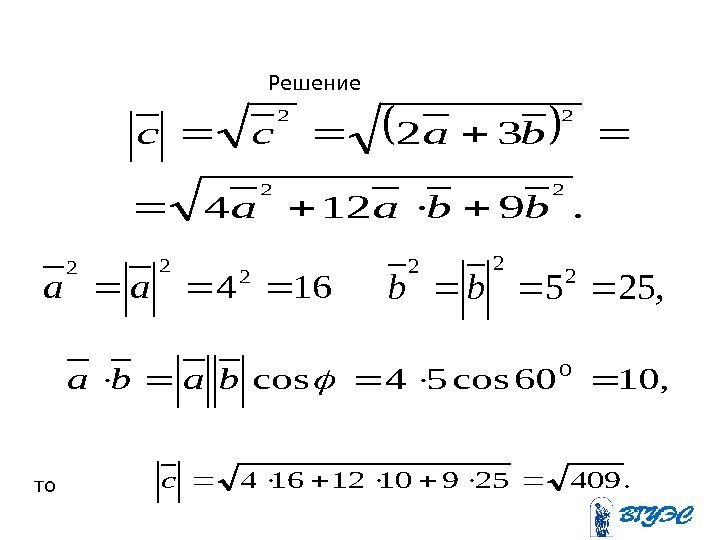






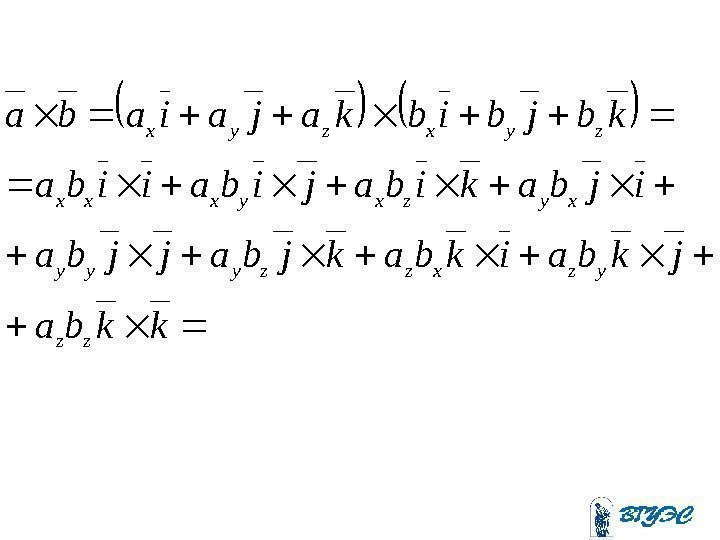
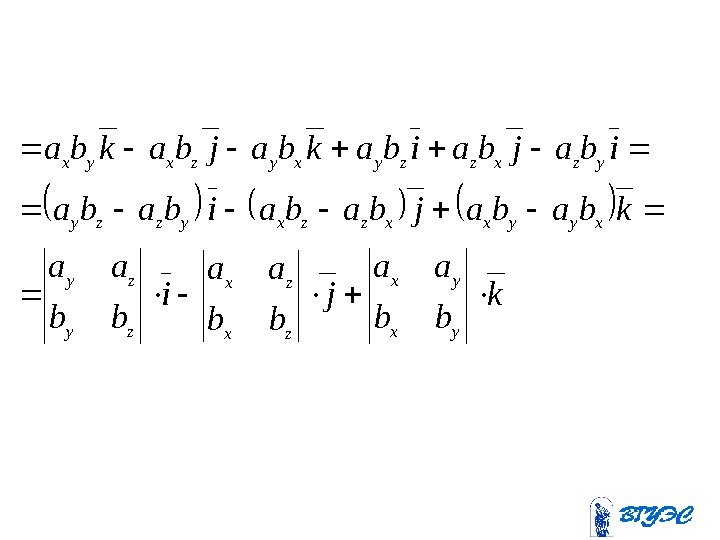


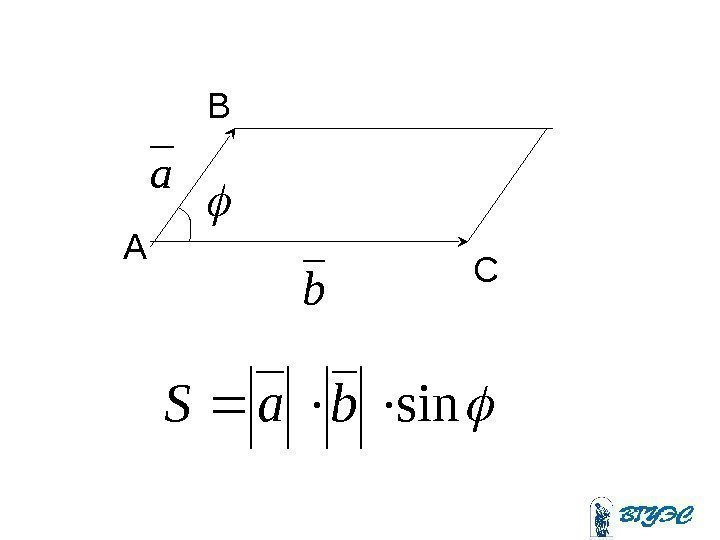
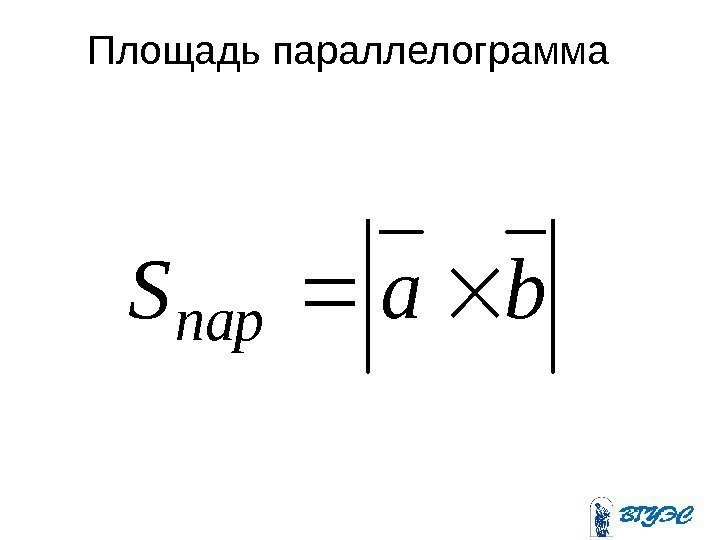
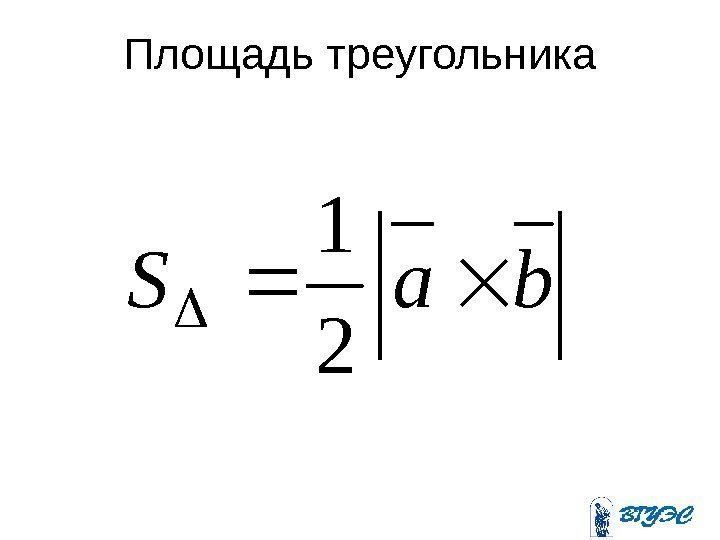


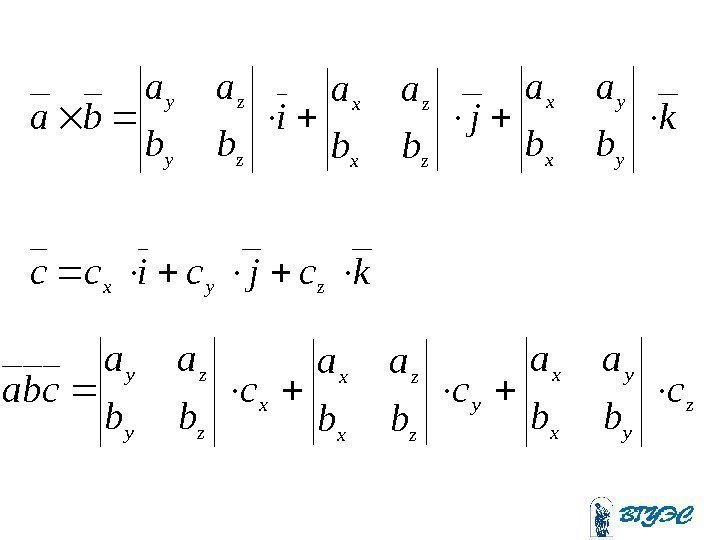

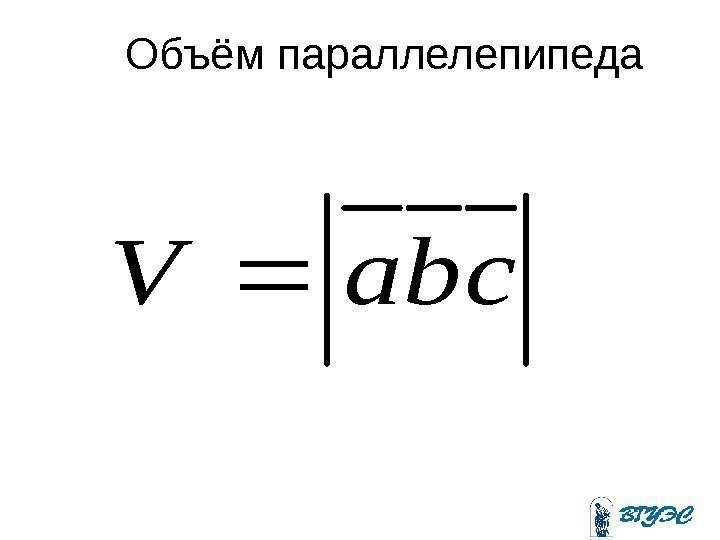

4.v_e_k_t_o_r_y.ppt
- Размер: 733.0 Кб
- Автор:
- Количество слайдов: 99
Описание презентации В е к т о р ы. О по слайдам
 В е к т о р ы. О с н о в н ы е п о н я т и я.
В е к т о р ы. О с н о в н ы е п о н я т и я.
 Вектором называется направленный отрезок. Обозначают векторы символами или , где А- начало, а B -конец направленного отрезка. a a AB А В a
Вектором называется направленный отрезок. Обозначают векторы символами или , где А- начало, а B -конец направленного отрезка. a a AB А В a
 • Нулевым вектором (обозначается ) называется вектор, начало и конец которого совпадают. • Расстояние между началом и концом вектора называется его длиной , или модулем или абсолютной величиной. • Векторы называются коллинеарными , если они расположены на одной прямой или на параллельных прямых
• Нулевым вектором (обозначается ) называется вектор, начало и конец которого совпадают. • Расстояние между началом и концом вектора называется его длиной , или модулем или абсолютной величиной. • Векторы называются коллинеарными , если они расположены на одной прямой или на параллельных прямых
 • Векторы называются компланарными , если они параллельны одной плоскости. • Векторы называются равными , если они сонаправлены и имеют равные длины. • Два вектора, имеющие равные длины, коллинеарные и противоположно направленные, наз. противоположными.
• Векторы называются компланарными , если они параллельны одной плоскости. • Векторы называются равными , если они сонаправлены и имеют равные длины. • Два вектора, имеющие равные длины, коллинеарные и противоположно направленные, наз. противоположными.
 • Вектор, длина которого равна 1, называется единичным вектором или ортом. • Ортом вектора называется соноправленный ему вектор и обозначается a 0 a
• Вектор, длина которого равна 1, называется единичным вектором или ортом. • Ортом вектора называется соноправленный ему вектор и обозначается a 0 a
 Линейные операции над векторами
Линейные операции над векторами
 Линейными операциями называют операции сложения и вычитания векторов и умножения вектора на число.
Линейными операциями называют операции сложения и вычитания векторов и умножения вектора на число.
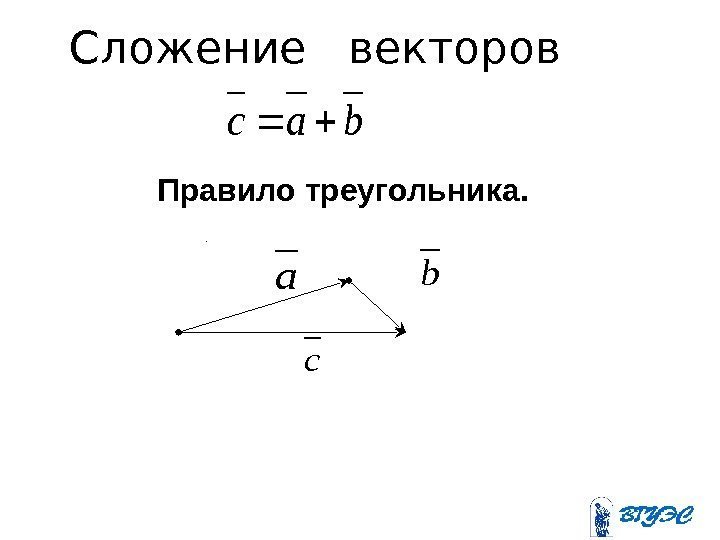
 Сложение векторовab c Правило треугольника. bac c
Сложение векторовab c Правило треугольника. bac c
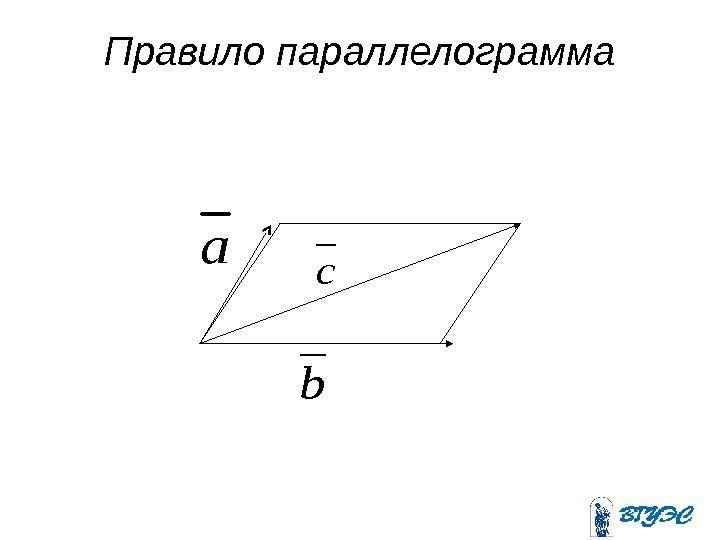
 Правило параллелограммаa b c
Правило параллелограммаa b c
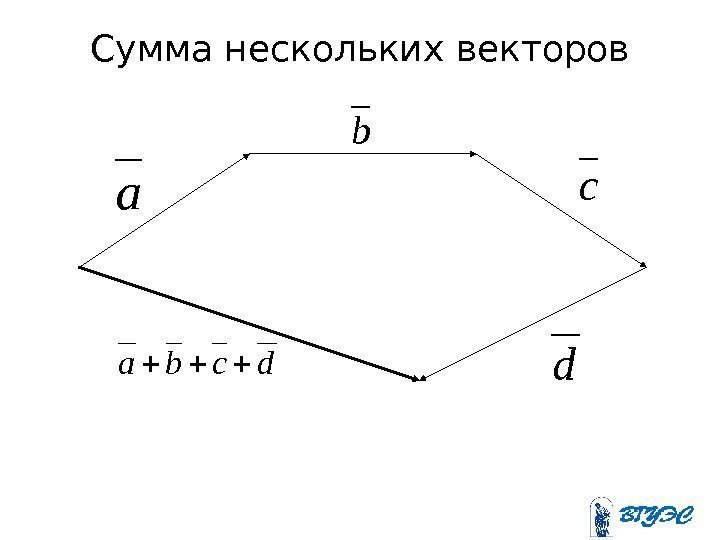
 Сумма нескольких векторов ab c d dcba
Сумма нескольких векторов ab c d dcba
 Вычитание векторовa b c bac
Вычитание векторовa b c bac
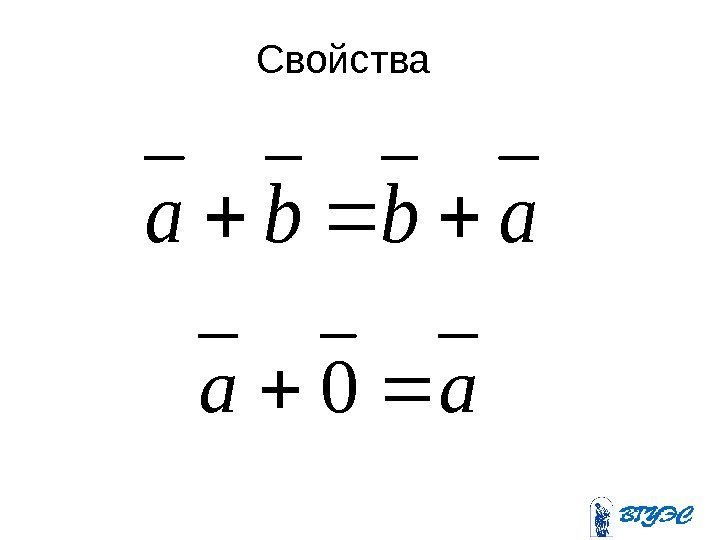 Свойства abba aa
Свойства abba aa
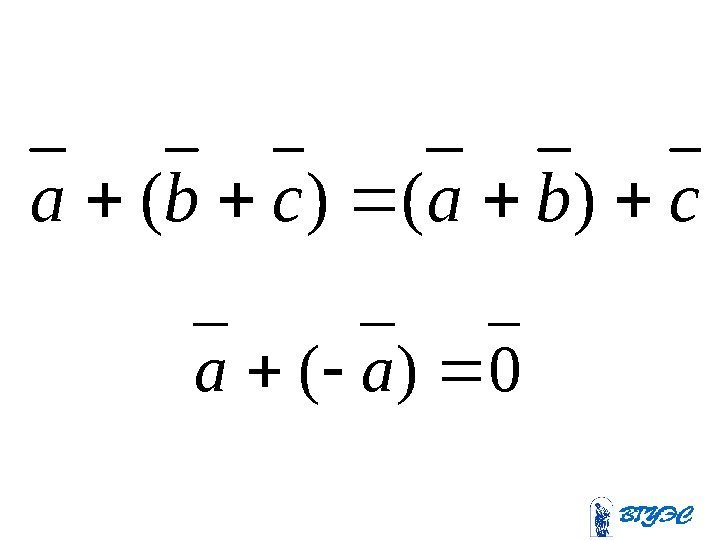 cbacba)()( 0)(aa
cbacba)()( 0)(aa
 Умножение вектора на число Произведением вектора на действительное число называется вектор (обозначают ), определяемый следующими условиями: 1. , 2. при и при . a bab ab 0 ab
Умножение вектора на число Произведением вектора на действительное число называется вектор (обозначают ), определяемый следующими условиями: 1. , 2. при и при . a bab ab 0 ab
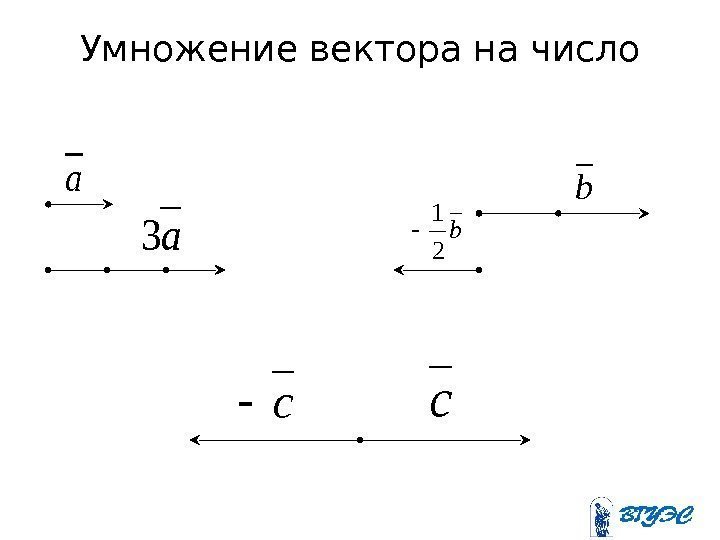
 Умножение вектора на числоa a 3 b b 2 1 cc
Умножение вектора на числоa a 3 b b 2 1 cc
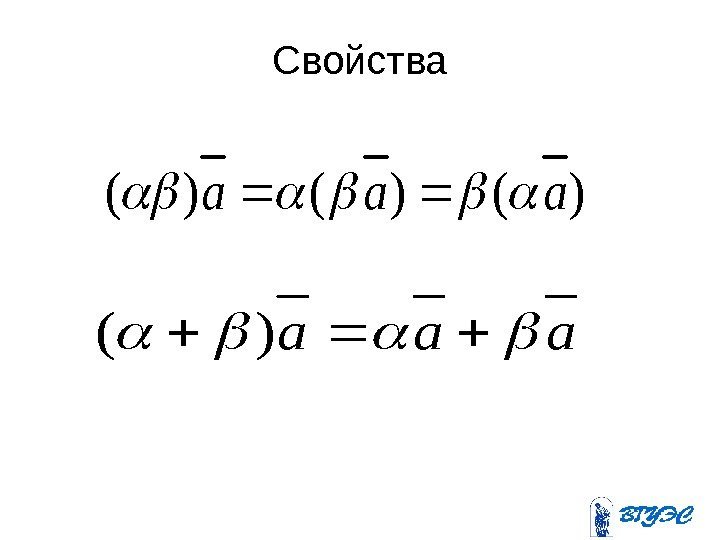 Свойства)()()(aaa aaa)(
Свойства)()()(aaa aaa)(
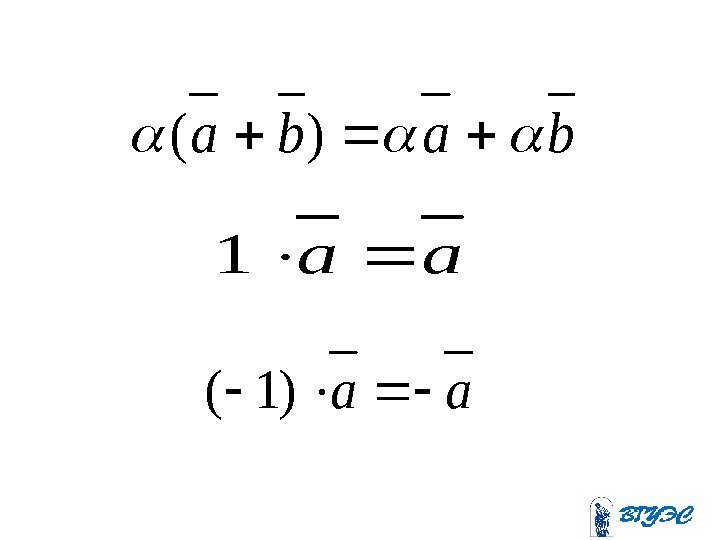 baba)( aa 1 aa)1(
baba)( aa 1 aa)1(
 • Отсюда вытекает условие коллинеарности векторов: два ненулевых вектора коллинеарны тогда и только тогда, когда имеет место равенство • Если орт вектора , то и тогда. 0 , ab 0 aa 0 aaaa a a
• Отсюда вытекает условие коллинеарности векторов: два ненулевых вектора коллинеарны тогда и только тогда, когда имеет место равенство • Если орт вектора , то и тогда. 0 , ab 0 aa 0 aaaa a a
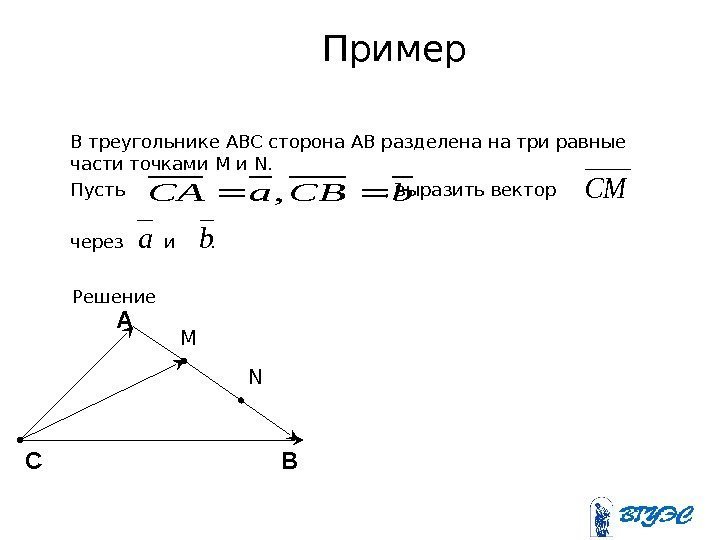
 Пример В треугольнике ABC сторона AB разделена на три равные части точками M и N. Пусть , выразить вектор через и . b. CBa. CA, CM a b Решение M NА ВС
Пример В треугольнике ABC сторона AB разделена на три равные части точками M и N. Пусть , выразить вектор через и . b. CBa. CA, CM a b Решение M NА ВС
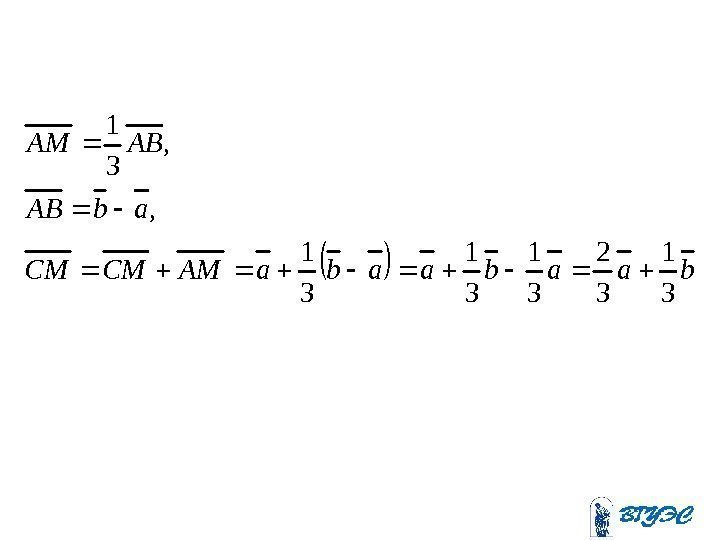 baabaaba. AMCMCM ab. AB ABAM 3 1 3 2 3 1 3 1 , ,
baabaaba. AMCMCM ab. AB ABAM 3 1 3 2 3 1 3 1 , ,
 Угол между двумя векторами
Угол между двумя векторами
 • Углом между векторами наз-ся наименьший угол , на который надо повернуть один из векторов до его совпадения со вторым. • Под углом между вектором и осью понимают угол между вектором и единичным вектором, расположенным на оси 0 l a
• Углом между векторами наз-ся наименьший угол , на который надо повернуть один из векторов до его совпадения со вторым. • Под углом между вектором и осью понимают угол между вектором и единичным вектором, расположенным на оси 0 l a
 Проекция вектора на ось и составляющая вектора на оси
Проекция вектора на ось и составляющая вектора на оси
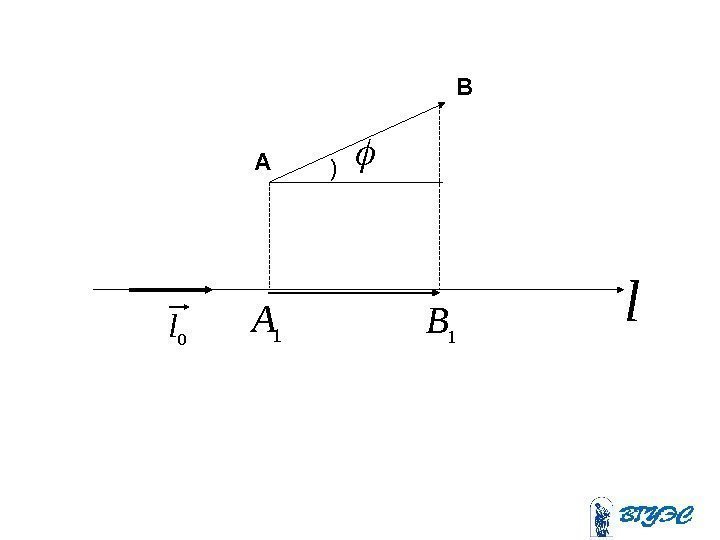
 A B 1 A 1 B l 0 l )
A B 1 A 1 B l 0 l )
 • Проекцией вектора на ось называется разность между координатами проекций конца и начала вектора на эту ось. Обозначается . ABl 12 xx ABпр l
• Проекцией вектора на ось называется разность между координатами проекций конца и начала вектора на эту ось. Обозначается . ABl 12 xx ABпр l
 • Если — острый, то если — тупой, то если , то ; 0 ABпрl 2 . 0 ABпр l
• Если — острый, то если — тупой, то если , то ; 0 ABпрl 2 . 0 ABпр l
 • Вектор наз. составляющей вектора по оси и обозначается 11 BA ABl 012011 lxxl. ABпр. ABсост. BAll
• Вектор наз. составляющей вектора по оси и обозначается 11 BA ABl 012011 lxxl. ABпр. ABсост. BAll
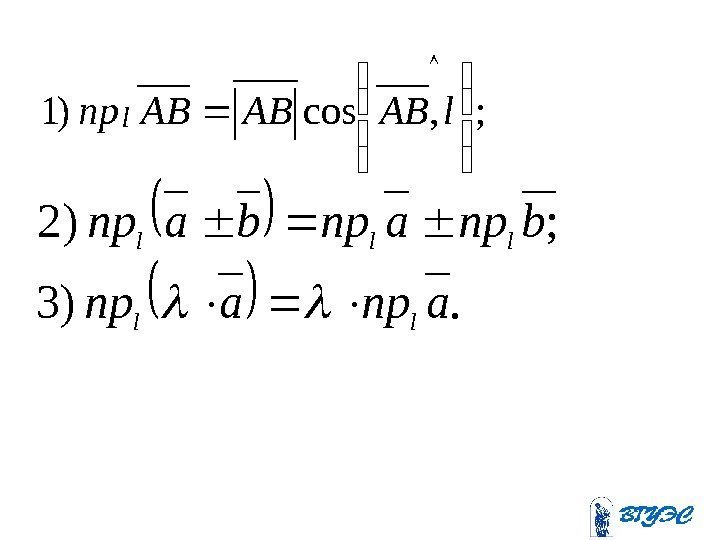 . )3 ; )2 aпрaпр bпрaпрbaпрll lll ; , cos )1 l. ABАВABпр l
. )3 ; )2 aпрaпр bпрaпрbaпрll lll ; , cos )1 l. ABАВABпр l
 Линейная зависимость векторов
Линейная зависимость векторов
 • Векторы наз-ся линейно зависимыми, если существуют числа не все равные 0, для которых имеет место равенство n aaa, . . . , , 21 n , . . . , , 21 (*) 0. . . 2211 nn aaa
• Векторы наз-ся линейно зависимыми, если существуют числа не все равные 0, для которых имеет место равенство n aaa, . . . , , 21 n , . . . , , 21 (*) 0. . . 2211 nn aaa
 n n aaaa 1 3 2 1. . . nn aaaa. . . 33221 векторовкомбинация линейнаяaaa nn . . .
n n aaaa 1 3 2 1. . . nn aaaa. . . 33221 векторовкомбинация линейнаяaaa nn . . .
 • Векторы наз-ся линейно независимыми, если равенство выполняется только при n aaa, . . . , , 21 0. . . 21 n 0. . . 2211 nn aaa
• Векторы наз-ся линейно независимыми, если равенство выполняется только при n aaa, . . . , , 21 0. . . 21 n 0. . . 2211 nn aaa
 • Для того чтобы векторы были линейно зависимы, необходимо и достаточно, чтобы хотя бы один из этих векторов можно было представить в виде линейной комбинации остальных. • Всякие три вектора на плоскости линейно зависимы.
• Для того чтобы векторы были линейно зависимы, необходимо и достаточно, чтобы хотя бы один из этих векторов можно было представить в виде линейной комбинации остальных. • Всякие три вектора на плоскости линейно зависимы.
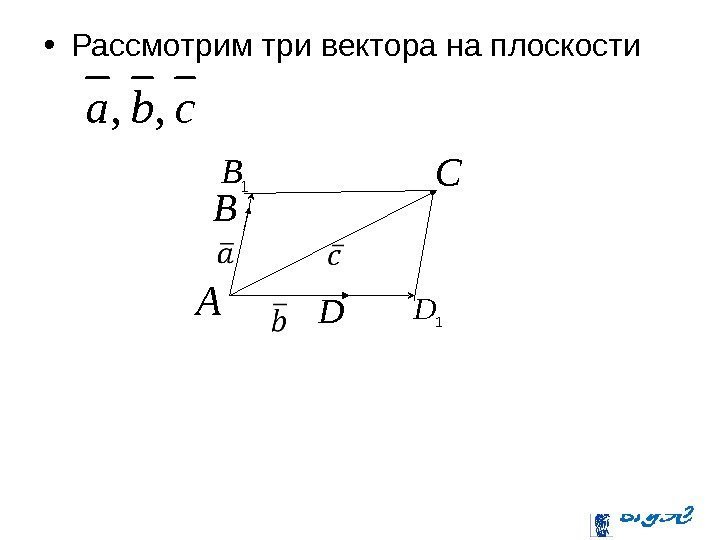
 • Рассмотрим три вектора на плоскости 1 D 1 B A C D B cba , ,
• Рассмотрим три вектора на плоскости 1 D 1 B A C D B cba , ,
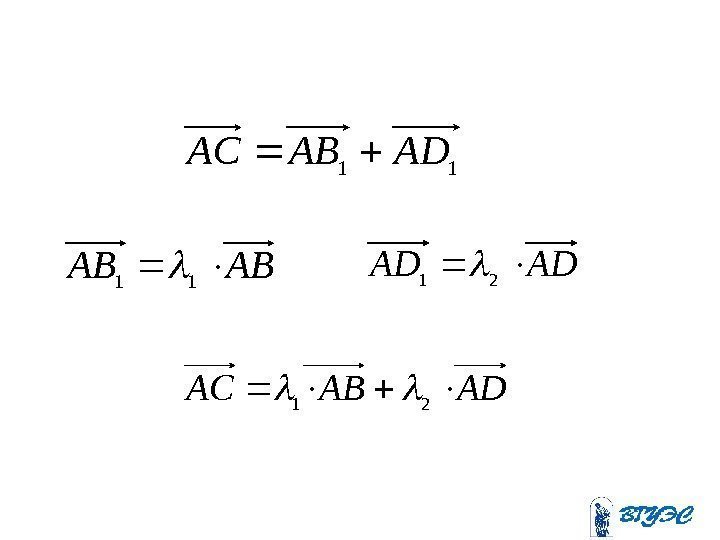
 • Для того чтобы два вектора были линейно независимы, необходимо и достаточно, чтобы они были неколлинеарны. • Для того чтобы три вектора в пространстве были линейно независимы, необходимо и достаточно, чтобы они были некомпланарны.
• Для того чтобы два вектора были линейно независимы, необходимо и достаточно, чтобы они были неколлинеарны. • Для того чтобы три вектора в пространстве были линейно независимы, необходимо и достаточно, чтобы они были некомпланарны.
 • Максимальное число линейно независимых векторов на плоскости равно двум. • Максимальное число линейно независимых векторов в пространстве равно трём.
• Максимальное число линейно независимых векторов на плоскости равно двум. • Максимальное число линейно независимых векторов в пространстве равно трём.
 Базис на плоскости и в пространстве
Базис на плоскости и в пространстве
 • Базисом на плоскости называют два любых линейно независимых вектора. Т. Разложение любого вектора на плоскости по базису является единственным a cb ,
• Базисом на плоскости называют два любых линейно независимых вектора. Т. Разложение любого вектора на плоскости по базису является единственным a cb ,
 • Базисом в пространстве называют три любых линейно независимых вектора. Т. Разложение любого вектора в пространстве по базису является единственнымa dcb , ,
• Базисом в пространстве называют три любых линейно независимых вектора. Т. Разложение любого вектора в пространстве по базису является единственнымa dcb , ,
 Прямоугольный декартовый базис
Прямоугольный декартовый базис
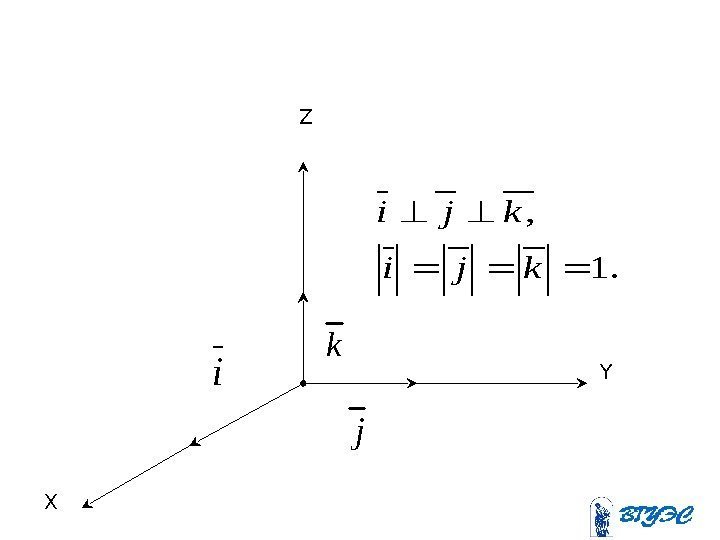
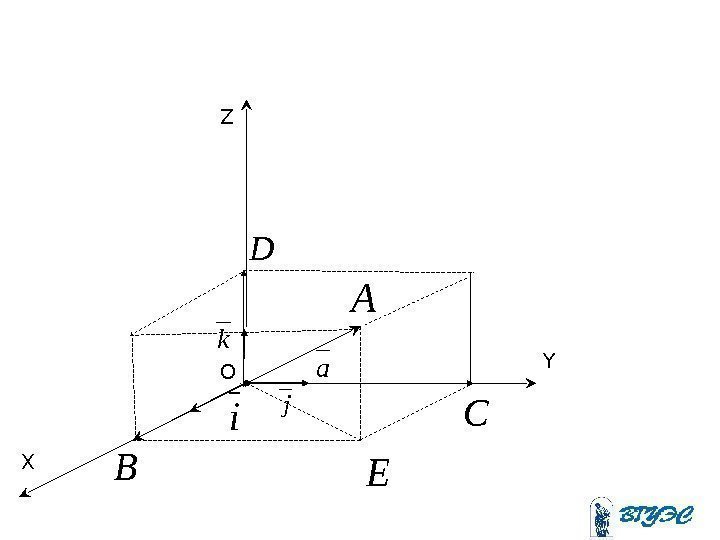
 i jk. Z Y X. 1 , kji
i jk. Z Y X. 1 , kji
 Oa i j X YZ k
Oa i j X YZ k
 Oa i j X YZ k
Oa i j X YZ k
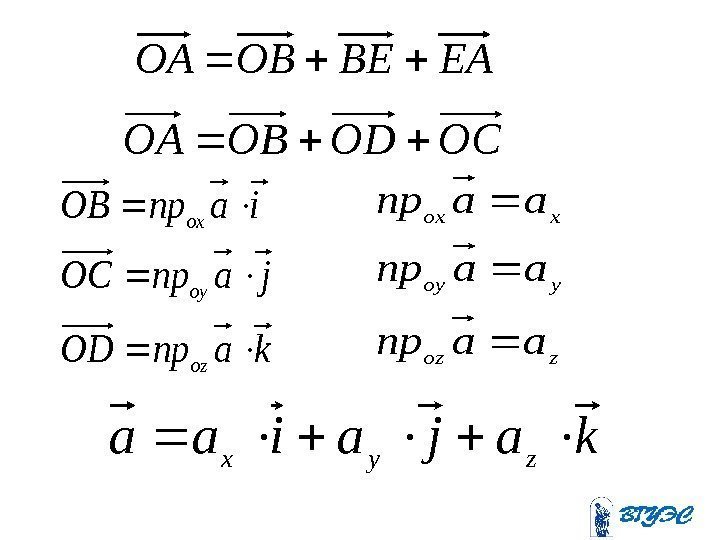 EABEOBOA OCODOBOA kaпр. OD jaпр. OC iaпр. OB oz oy ox zoz yoy xox aaпр kajaiaa zyx
EABEOBOA OCODOBOA kaпр. OD jaпр. OC iaпр. OB oz oy ox zoz yoy xox aaпр kajaiaa zyx
 Линейные операции над векторами в координатной форме
Линейные операции над векторами в координатной форме
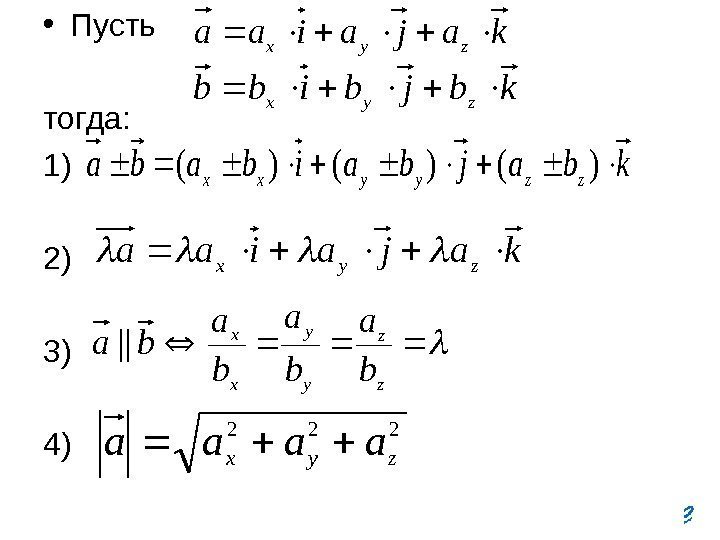 • Пусть тогда: 1) 2) 3) 4)kajaiaazyx kbjbibb zyx kbajbaibabazzyyxx)()()( kajaiaa zyx z z y y x x b a b a ba|| 222 zyx aaaa
• Пусть тогда: 1) 2) 3) 4)kajaiaazyx kbjbibb zyx kbajbaibabazzyyxx)()()( kajaiaa zyx z z y y x x b a b a ba|| 222 zyx aaaa
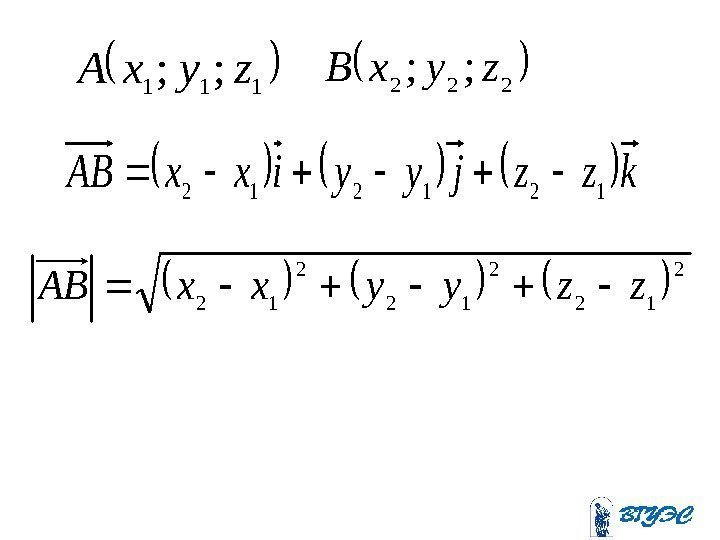 111 ; ; zyx. A 222 ; ; zyx. B kzzjyyixx. AB 121212 2 12 zzyyxx.
111 ; ; zyx. A 222 ; ; zyx. B kzzjyyixx. AB 121212 2 12 zzyyxx.
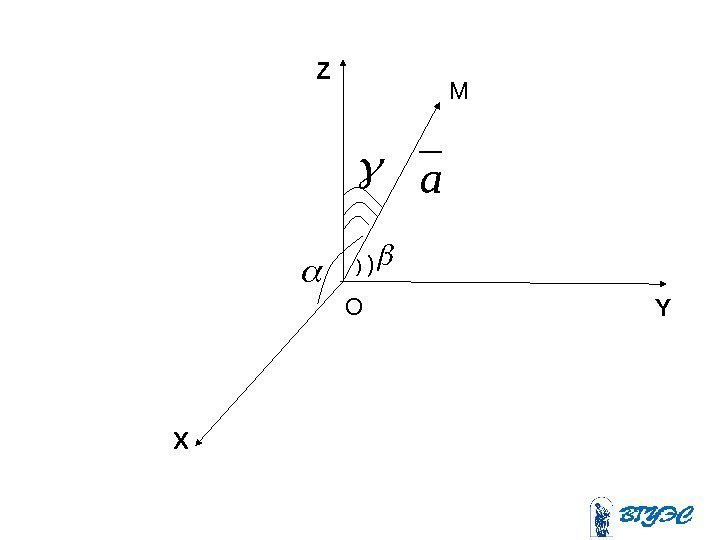
 Направляющие косинусы
Направляющие косинусы
 X YZ M O ) ) a
X YZ M O ) ) a
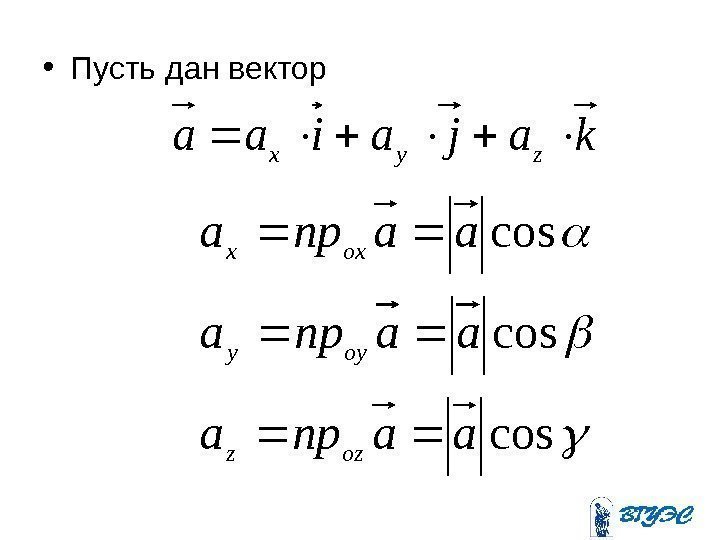 • Пусть дан вектор kajaiaazyx cos cos aaпрa ozz oyy oxx
• Пусть дан вектор kajaiaazyx cos cos aaпрa ozz oyy oxx
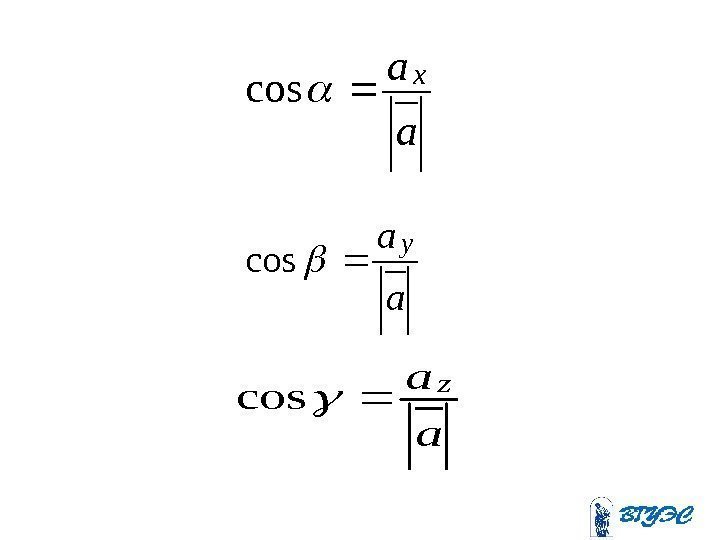 a ax cos a ay cos a az cos
a ax cos a ay cos a az cos
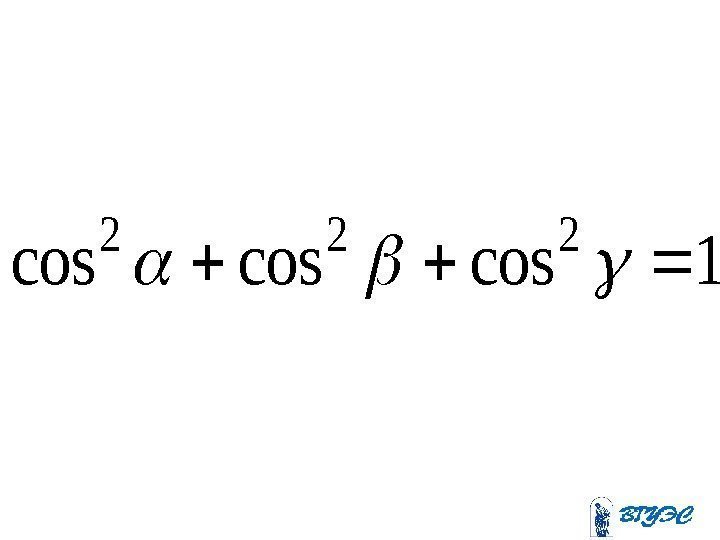 1 coscoscos
1 coscoscos
 Координаты единичного вектора, cos, cos 0 a
Координаты единичного вектора, cos, cos 0 a
 Пример Найти косинусы углов, которые, вектор составляет с осями координат, если А (1, 2, 3) и В (2, 4, 5). AB 32 cos, 31 cos , 3221 , 2; 2; 1 35; 24; 12 222 тогда ABABРешение.
Пример Найти косинусы углов, которые, вектор составляет с осями координат, если А (1, 2, 3) и В (2, 4, 5). AB 32 cos, 31 cos , 3221 , 2; 2; 1 35; 24; 12 222 тогда ABABРешение.
 Деление отрезка в данном отношении
Деление отрезка в данном отношении
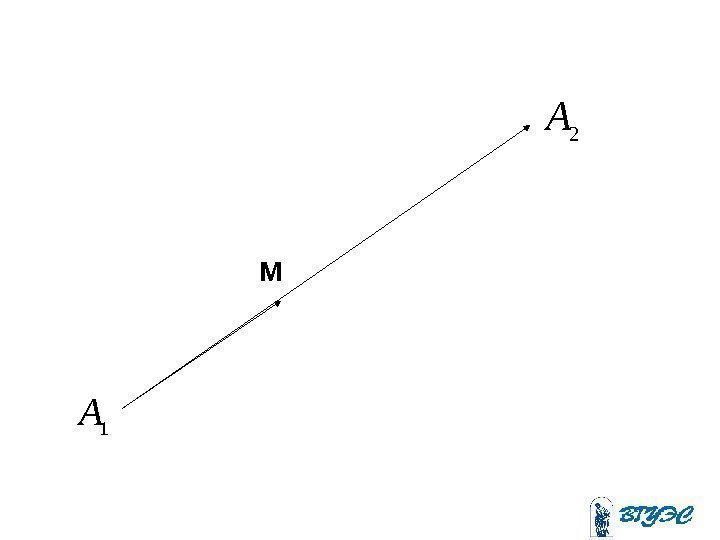
 1 A 2 AM
1 A 2 AM
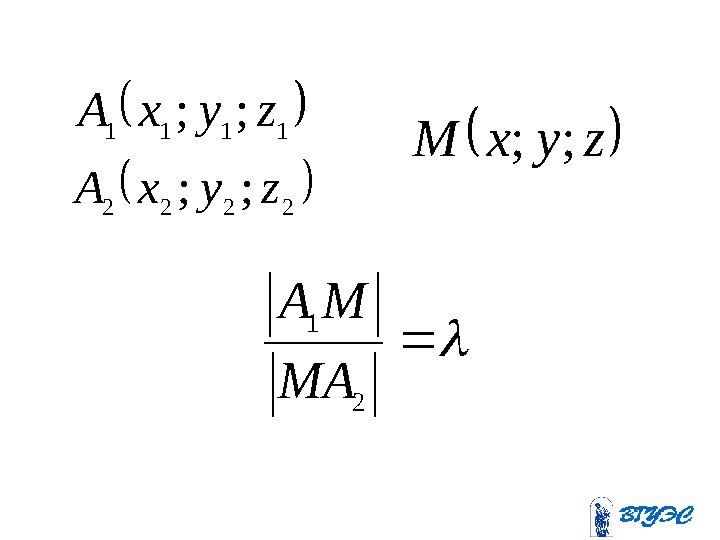 1111 ; ; zyx. A 2222 ; ; zyx. A zyx. M; ; 2 1 MA M
1111 ; ; zyx. A 2222 ; ; zyx. A zyx. M; ; 2 1 MA M
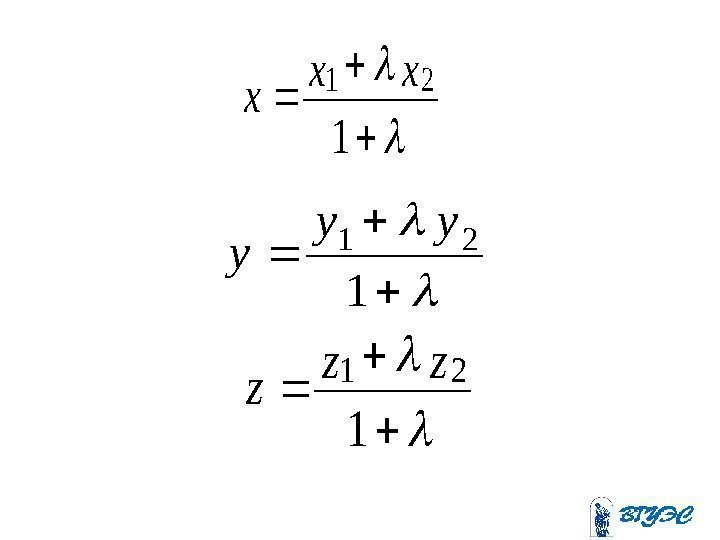 1 21 xx x 1 21 yy y 1 21 zz z
1 21 xx x 1 21 yy y 1 21 zz z
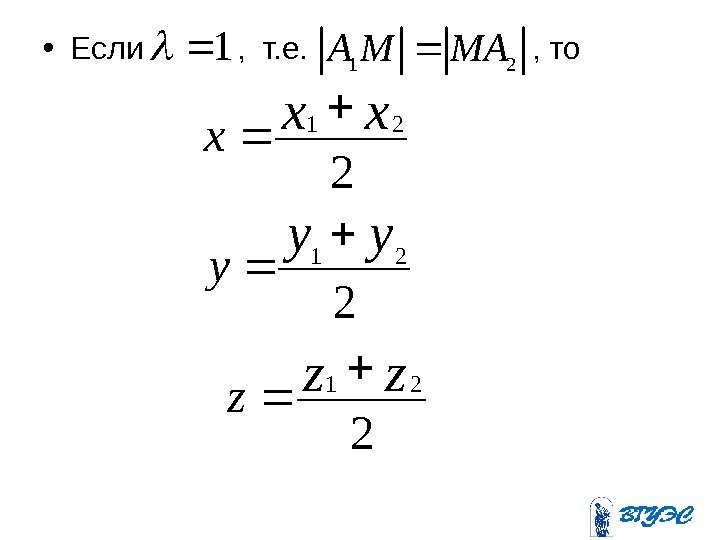 • Если , т. е. , то 2 21 xx x 1 21 MAMA 2 21 yy y 2 21 zz z
• Если , т. е. , то 2 21 xx x 1 21 MAMA 2 21 yy y 2 21 zz z
 Скалярное произведение векторов Скалярным произведением векторов называется произведение их модулей на косинус угла между ними.
Скалярное произведение векторов Скалярным произведением векторов называется произведение их модулей на косинус угла между ними.
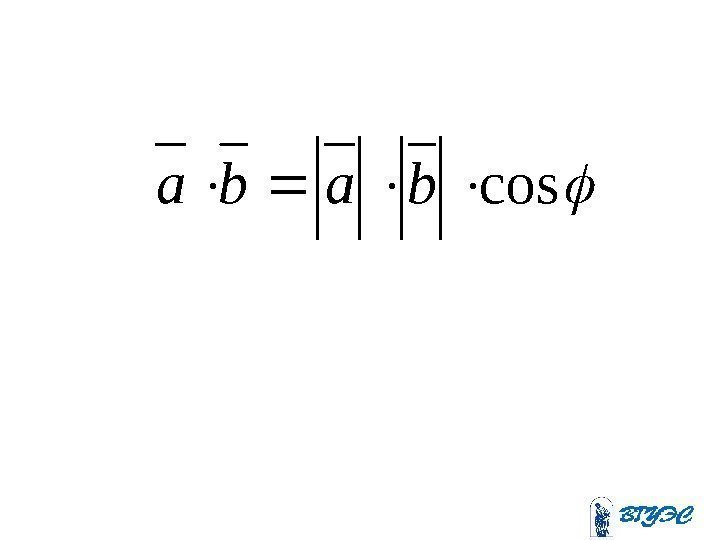 cosbaba
cosbaba
 Условие перпендикулярности векторов 0 baba
Условие перпендикулярности векторов 0 baba
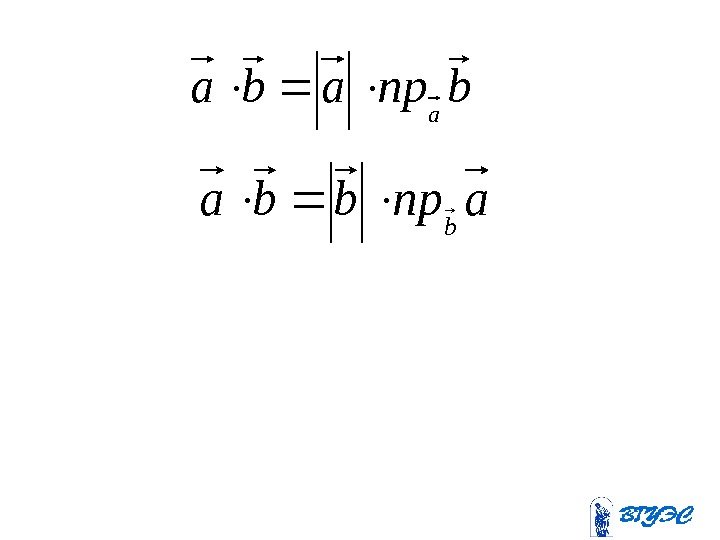 bпрaba a aпрbba b
bпрaba a aпрbba b
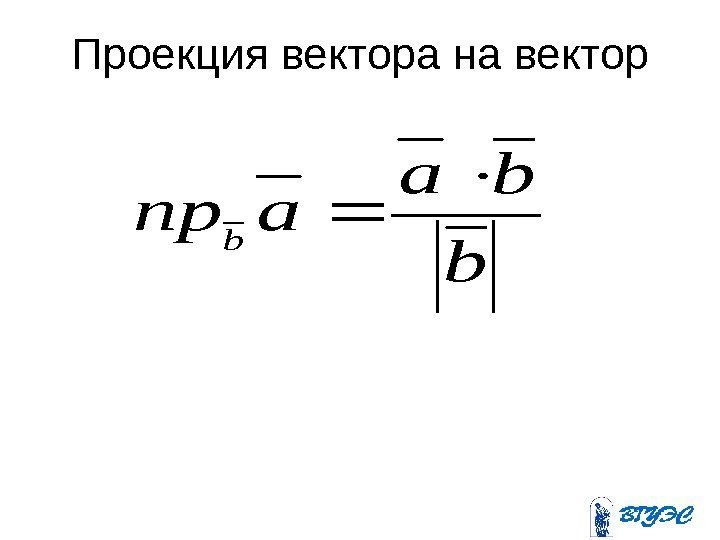 Проекция вектора на векторb ba aпр b
Проекция вектора на векторb ba aпр b
 Угол между векторами. cos 2 2 2 2 1 2 1 212121 zyxzyx zzyyxx ba ba
Угол между векторами. cos 2 2 2 2 1 2 1 212121 zyxzyx zzyyxx ba ba
 Физический смысл скалярного произведения Работа постоянной силы на прямолинейном участке пути равна скалярному произведению вектора силы на вектор перемещения.
Физический смысл скалярного произведения Работа постоянной силы на прямолинейном участке пути равна скалярному произведению вектора силы на вектор перемещения.
 Физический смысл скалярного произведения Fl. FA l
Физический смысл скалярного произведения Fl. FA l
 Свойства скалярного произведения abba )1)()()( )2 bababa
Свойства скалярного произведения abba )1)()()( )2 bababa
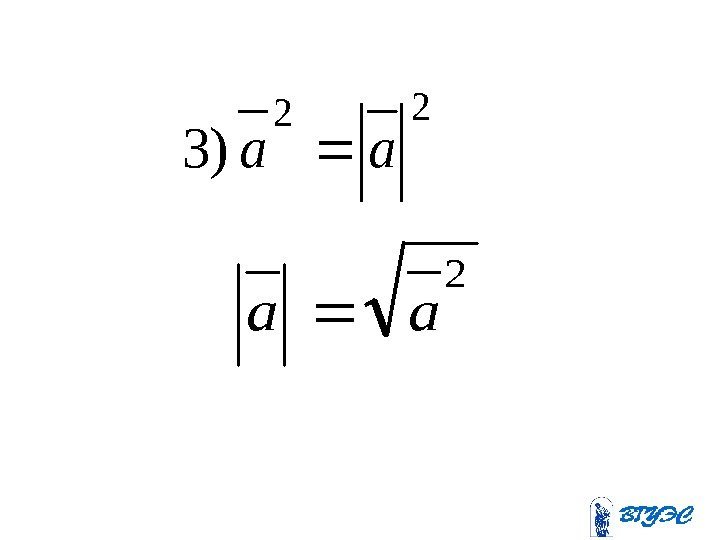 2 2 )3 aa 2 aa
2 2 )3 aa 2 aa
 • Пусть даны два вектораkajaiaa zyx kbjbibb zyx
• Пусть даны два вектораkajaiaa zyx kbjbibb zyx
 Найдем скалярное произведение этих векторов =)(kajaia zyx)(kbjbibzyx zzyyxx bababa 1 1 1 22 22 22 kkkk jjjj iiii 0 0 0 ki kj ji
Найдем скалярное произведение этих векторов =)(kajaia zyx)(kbjbibzyx zzyyxx bababa 1 1 1 22 22 22 kkkk jjjj iiii 0 0 0 ki kj ji
 Примерbac 324 a 5 b ab. c Дан вектор , причем , , угол между векторами и равен. 60 0 Найти модуль вектора
Примерbac 324 a 5 b ab. c Дан вектор , причем , , угол между векторами и равен. 60 0 Найти модуль вектора
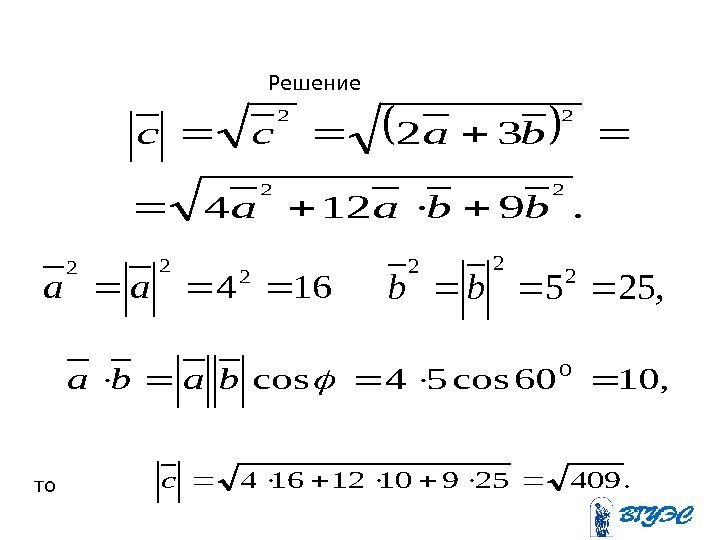 . 9124 32 22 22 bbaa baсс 164 2 22 aa, 255 2 22 bb , 1060 cos 54 cos 0 baba. 4092591012164 c. Решение то
. 9124 32 22 22 bbaa baсс 164 2 22 aa, 255 2 22 bb , 1060 cos 54 cos 0 baba. 4092591012164 c. Решение то
 Векторное произведение векторов
Векторное произведение векторов
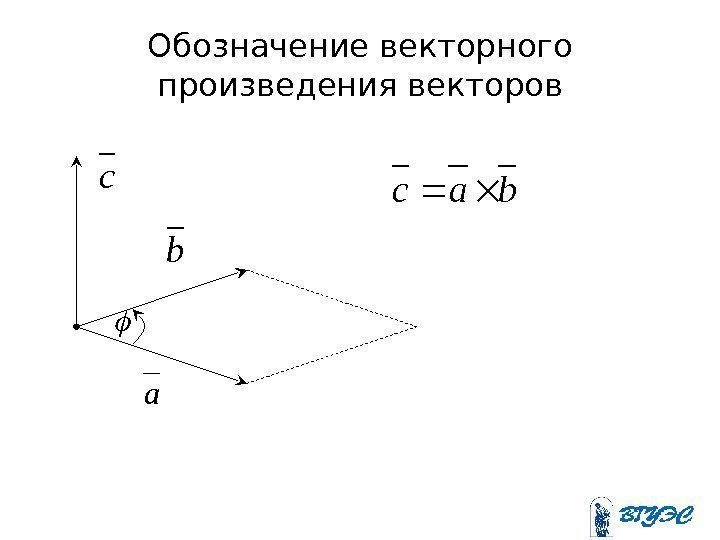
 • Векторным произведением вектора на вектор наз. вектор , удовлетворяющий следующим условиям: 1) 2) 3)векторы образуют правую тройкуa bbac sinbac cacb
• Векторным произведением вектора на вектор наз. вектор , удовлетворяющий следующим условиям: 1) 2) 3)векторы образуют правую тройкуa bbac sinbac cacb
 Понятие «правой» тройки векторов Тройку векторов называют правой , если направление вектора таково, что, смотря из его конца вдоль вектора, кратчайший поворот от вектора к вектору будет виден против движения часовой стрелки. , a, bc c a b , a , bс — правая тройка a b с
Понятие «правой» тройки векторов Тройку векторов называют правой , если направление вектора таково, что, смотря из его конца вдоль вектора, кратчайший поворот от вектора к вектору будет виден против движения часовой стрелки. , a, bc c a b , a , bс — правая тройка a b с
 Обозначение векторного произведения векторов ab c bac
Обозначение векторного произведения векторов ab c bac
 Свойства векторного произведенияabba 00 aba 0 b или ba 0 aa
Свойства векторного произведенияabba 00 aba 0 b или ba 0 aa
 Свойства векторного произведенияcbcacba)( )()()(bababa
Свойства векторного произведенияcbcacba)( )()()(bababa
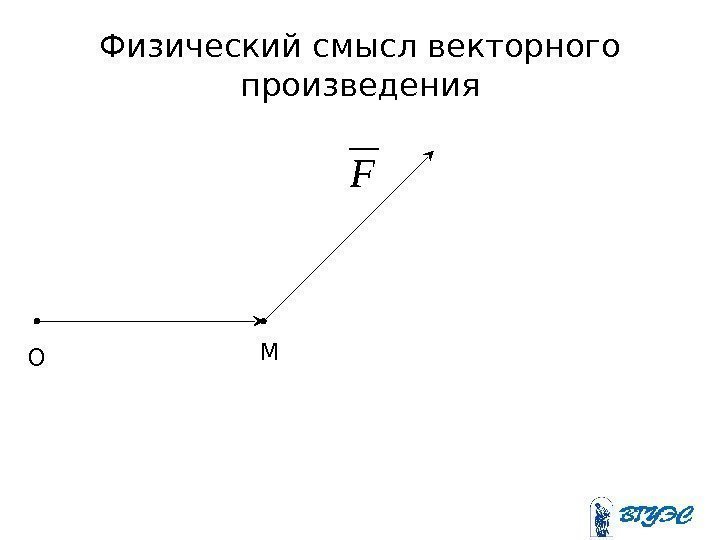
 Физический смысл векторного произведения. F O M
Физический смысл векторного произведения. F O M
 Физический смысл векторного произведения Если – сила, приложенная к точке М , то момент этой силы относительно точки О равен векторному произведению векторов и . F FOM
Физический смысл векторного произведения Если – сила, приложенная к точке М , то момент этой силы относительно точки О равен векторному произведению векторов и . F FOM
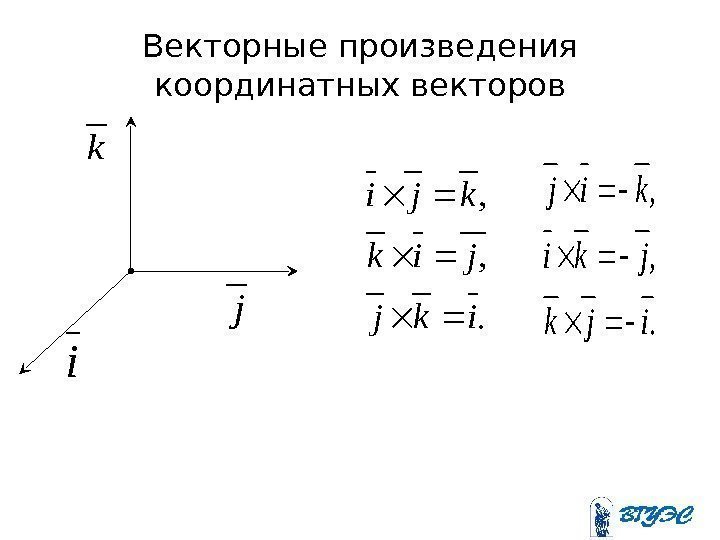
 Векторные произведения координатных векторовi j k. , , ikj jik kji . , , ijk jki kij
Векторные произведения координатных векторовi j k. , , ikj jik kji . , , ijk jki kij
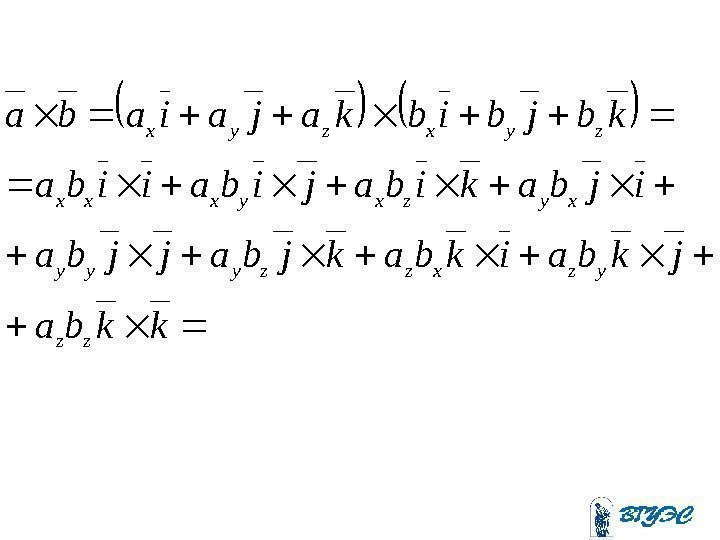 kkba jkbaikbakjbajjba ijbakibajibaiiba kbjbibkajaiaba zz yzxzzyyy xyzxyxxx zyxzyx
kkba jkbaikbakjbajjba ijbakibajibaiiba kbjbibkajaiaba zz yzxzzyyy xyzxyxxx zyxzyx
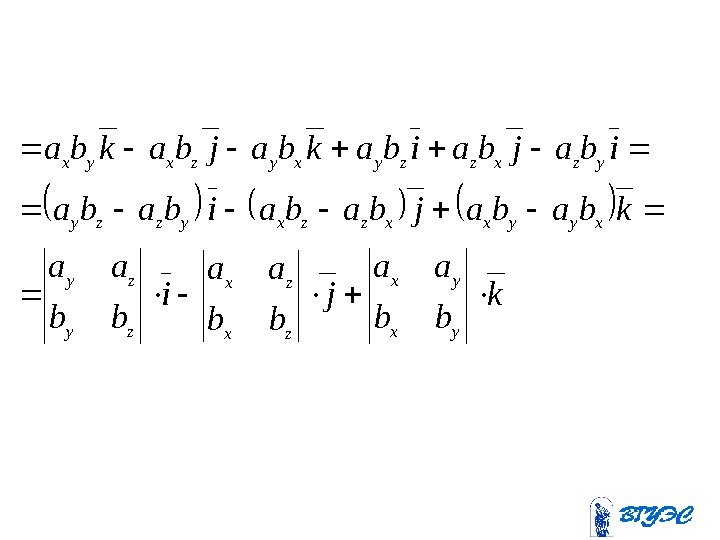 k bb aa j bb aa i bb aa kbabajbabaibaba ibajbaibakbajbakba yx yx zx zx zy zy xyyxxzzxyzzy yzxzzyxyzxyx
k bb aa j bb aa i bb aa kbabajbabaibaba ibajbaibakbajbakba yx yx zx zx zy zy xyyxxzzxyzzy yzxzzyxyzxyx
 Векторное произведение в координатной формеbzbybx azayax kji ba
Векторное произведение в координатной формеbzbybx azayax kji ba
 Пример Найти векторное произведение векторов. 43 , 32 kjib kjia Решение. 11513 13 32 43 12 41 13 413 132 kjikj ikji ba
Пример Найти векторное произведение векторов. 43 , 32 kjib kjia Решение. 11513 13 32 43 12 41 13 413 132 kjikj ikji ba
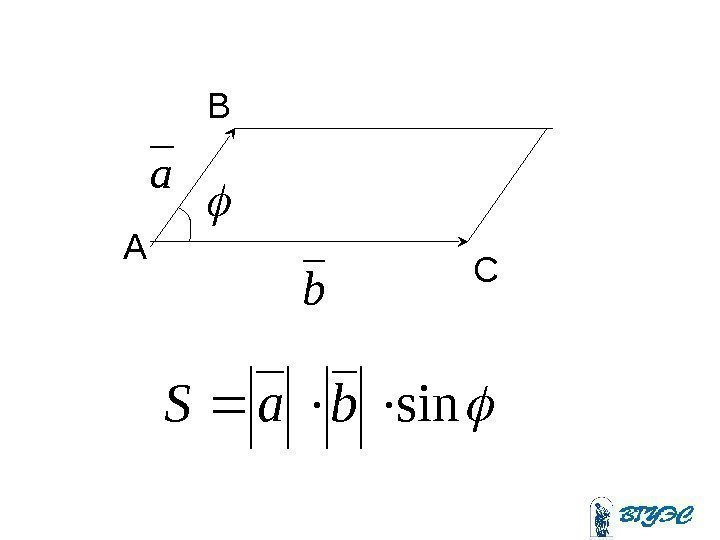 A B Ca b sinba. S
A B Ca b sinba. S
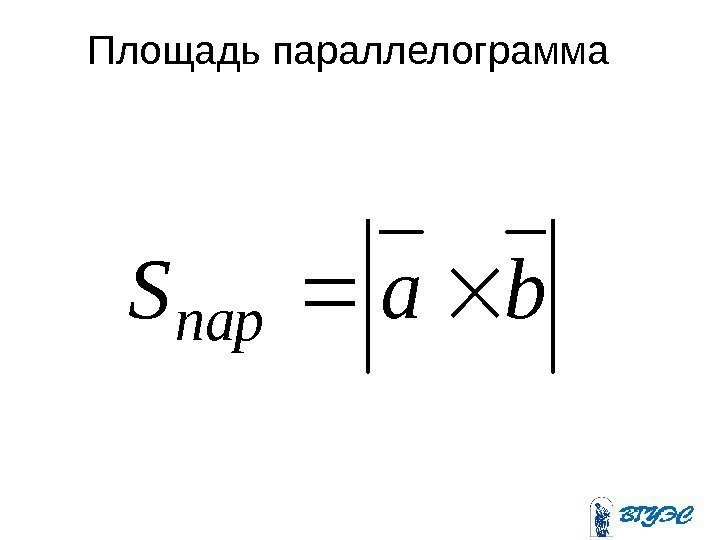 Площадь параллелограммаba. S пар
Площадь параллелограммаba. S пар
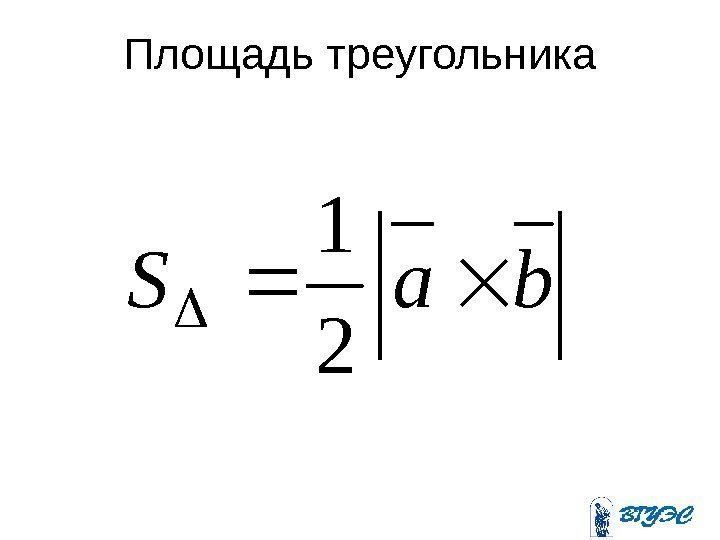 Площадь треугольникаba. S
Площадь треугольникаba. S
 Пример Найти если. 90, 1, 2 0 ba, 232 baba . 1490 sin 217 sin 77 6432 232 0 abab bbbaabaa baba Решение
Пример Найти если. 90, 1, 2 0 ba, 232 baba . 1490 sin 217 sin 77 6432 232 0 abab bbbaabaa baba Решение
 Смешанное произведение Смешанным произведением трёх векторов называется произведение вида : cba)(
Смешанное произведение Смешанным произведением трёх векторов называется произведение вида : cba)(
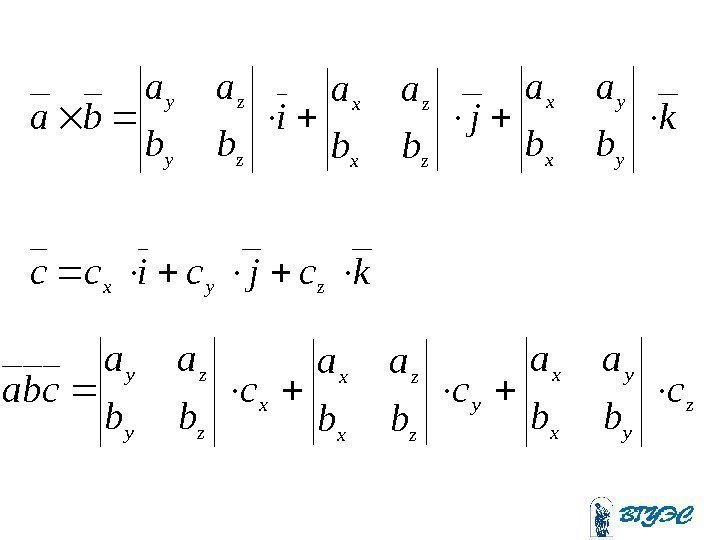 kcjcicc k bb aa j bb aa i bb aa bazyx yx yx zx zx zy zy z yx yx y zx zx x zy zy c bb aa cba
kcjcicc k bb aa j bb aa i bb aa bazyx yx yx zx zx zy zy z yx yx y zx zx x zy zy c bb aa cba
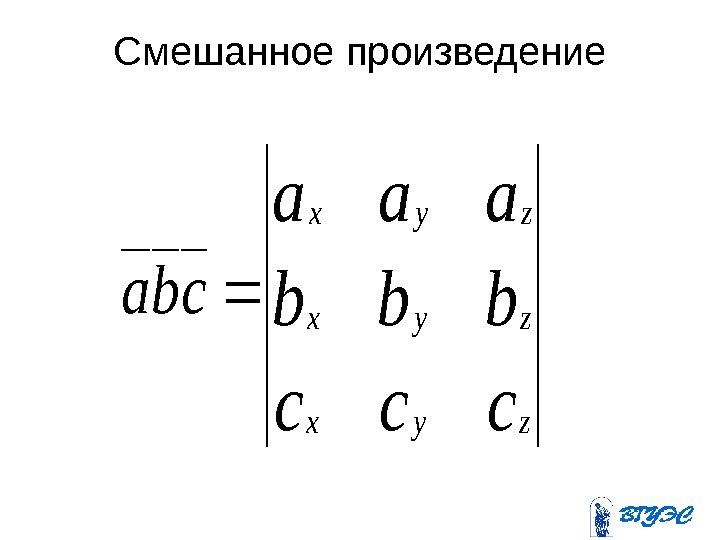
 Смешанное произведениеccc bbb aaa zyx zyx cba
Смешанное произведениеccc bbb aaa zyx zyx cba
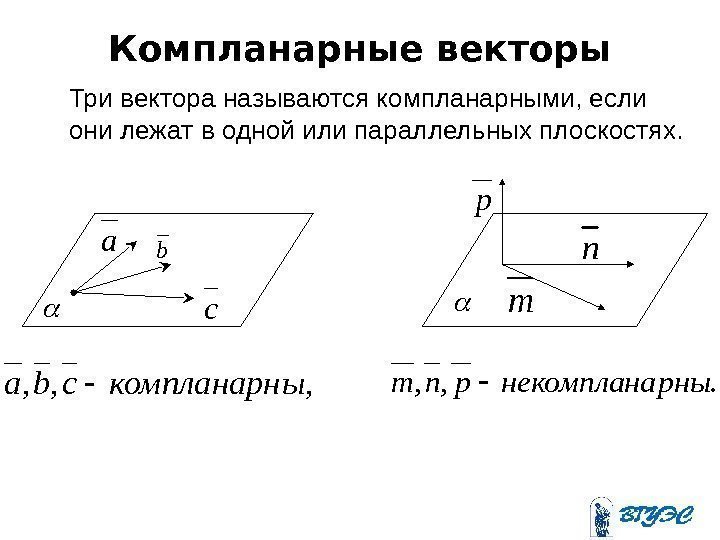
 Компланарные векторы Три вектора называются компланарными, если они лежат в одной или параллельных плоскостях. ab cm n p , , , ыкомпланарнcba. , , рнынекомпланаpnm
Компланарные векторы Три вектора называются компланарными, если они лежат в одной или параллельных плоскостях. ab cm n p , , , ыкомпланарнcba. , , рнынекомпланаpnm
 Условие компланарности трёх векторов cba , , . 0 zyx zyx ccc bbb aaa Если компланарны, то Элементами определителя являются координаты векторовcba, ,
Условие компланарности трёх векторов cba , , . 0 zyx zyx ccc bbb aaa Если компланарны, то Элементами определителя являются координаты векторовcba, ,
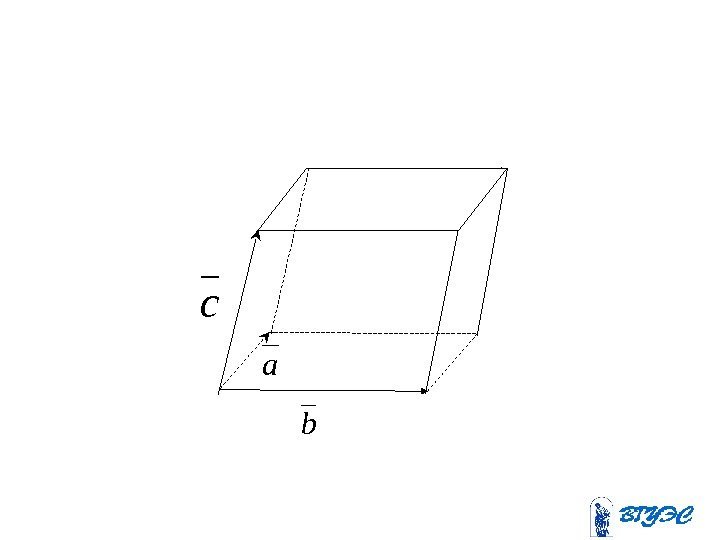
 a b c
a b c
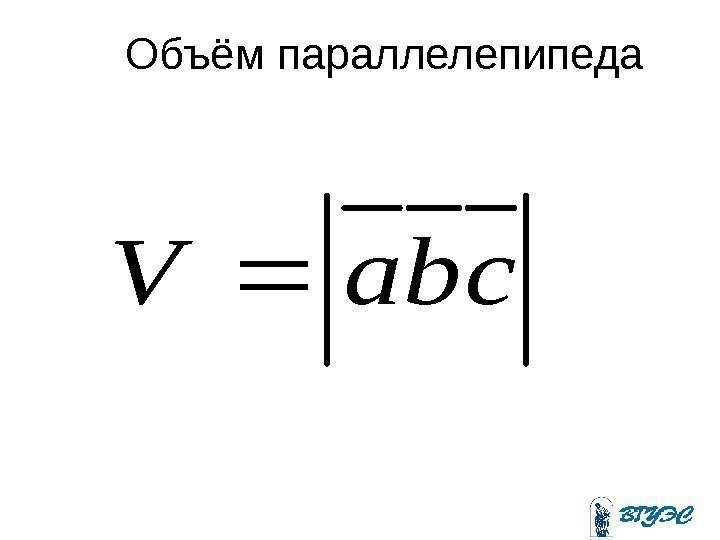 Объём параллелепипеда cba. V
Объём параллелепипеда cba. V
 Объём тетраэдра cba. V тет
Объём тетраэдра cba. V тет

