В 8 Задачи на использование графика производной функции

В 8. Задачи на использование графика производной функции и её геометрического смысла. Математика. 11 класс

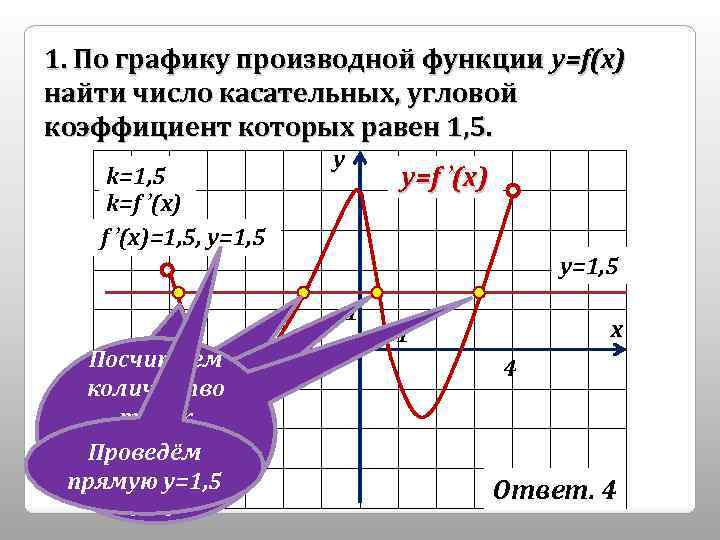1. По графику производной функции у=f(x) найти число касательных, угловой коэффициент которых равен 1, 5. k=1, 5 k=f ’(x)=1, 5, y=1, 5 у у=1, 5 1 Посчитаем -5 3 количество точек пересечения Проведём с графиком прямую у=1, 5 f’(x) у=f ’(x) х 1 4 Ответ. 4

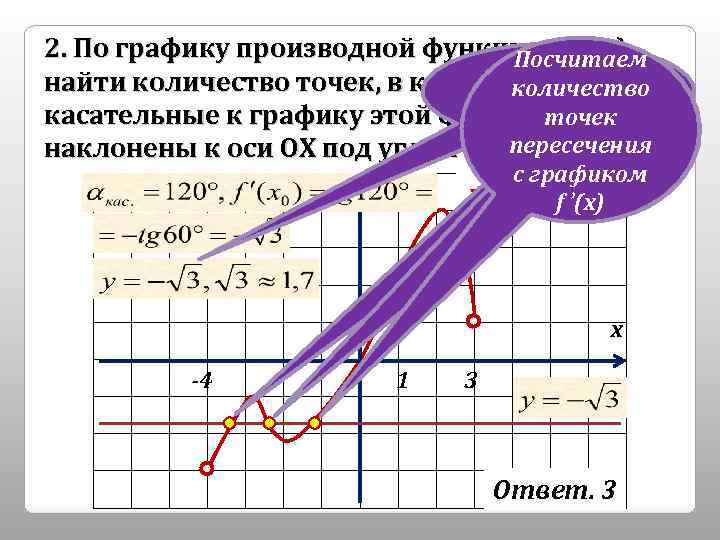2. По графику производной функции у=f(x) Посчитаем Проведём найти количество точек, в которых количество прямую касательные к графику этой функции у≈-1, 7 точек наклонены к оси ОХ под углом 120 пересечения ⁰. с графиком у=f ’(x)ff’(x) у 1 -4 х 1 3 Ответ. 3

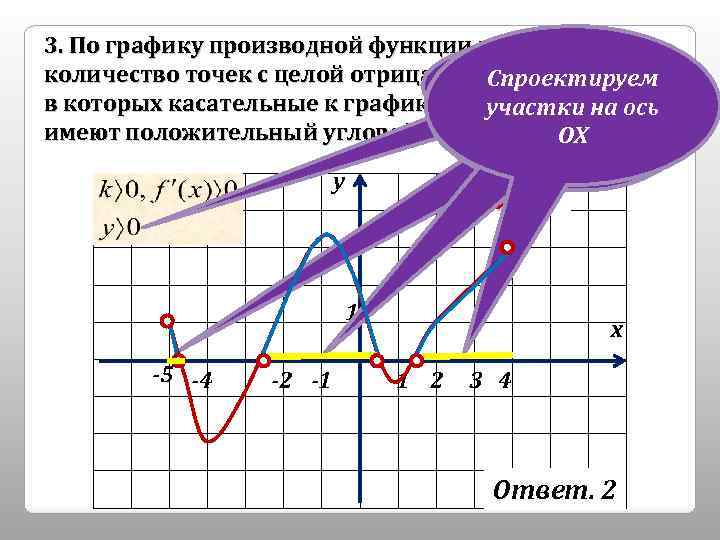3. По графику производной функции у=f(x) найти Выделим количество точек с целой отрицательной абсциссой, Спроектируем Спроектируе участки, на в которых касательные к графику этой функции ось участки на м участки которых… имеют положительный угловой коэффициент. ОХ… ОХ на ось у у=f ’(x) 1 -5 -4 -2 -1 х 1 2 3 4 Ответ. 2

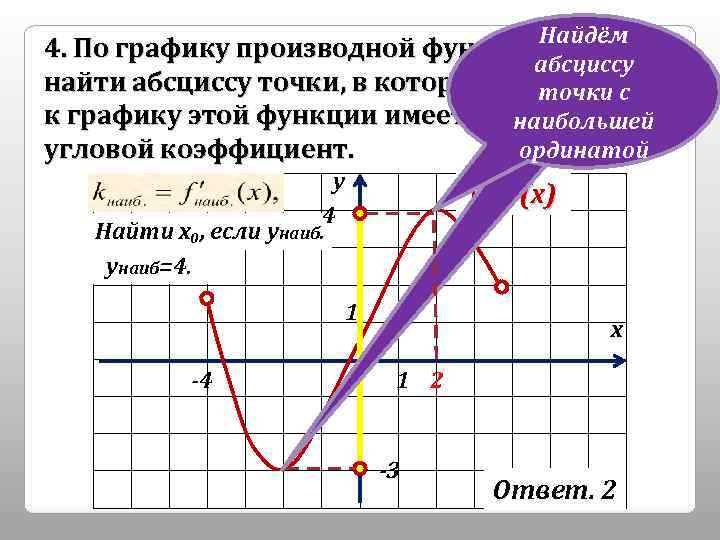Найдём 4. По графику производной функции у=f(x) Спроектируем абсциссу найти абсциссу точки, в которой касательная график насось точки ОУ к графику этой функции имеет наибольший наибольшей угловой коэффициент. ординатой у у=f ’(x) 4 Найти х₀, если унаиб=4. 1 -4 х 1 2 -3 Ответ. 2

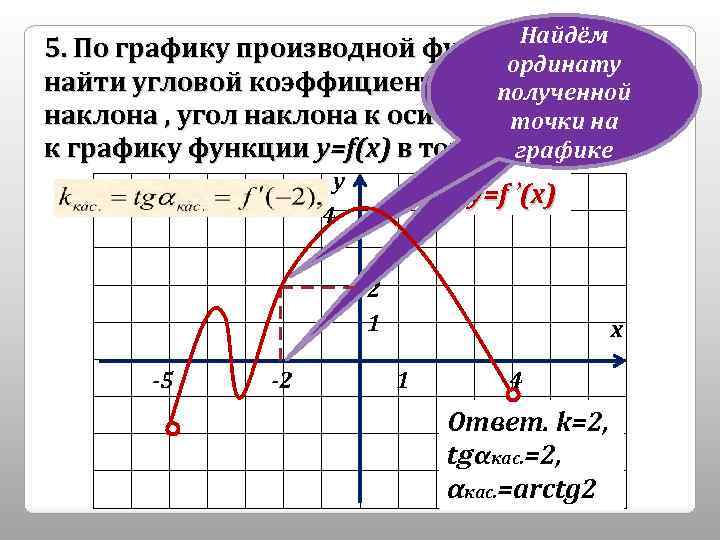Найдём 5. По графику производной функции у=f(x) Спроектируем ординату х₀=-2 на найти угловой коэффициент (тангенс угла полученной график наклона , угол наклона к оси ОХ) касательной точки на производной к графику функции у=f(x) в точке хграфике ₀= -2. у у=f ’(x) 4 2 1 -5 -2 х 1 4 Ответ. k=2, tgαкас. =2, αкас. =arctg 2

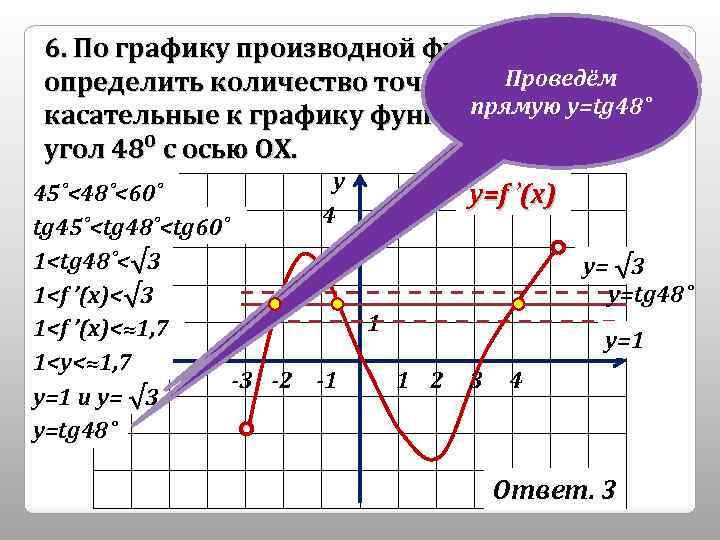6. По графику производной функции у=f(x) Проведём определить количество точек, в которых… прямые прямую y=tg 48˚ касательные к графику функции составляют угол 48⁰ с осью ОХ. у 45˚<48˚<60˚ 4 tg 45˚

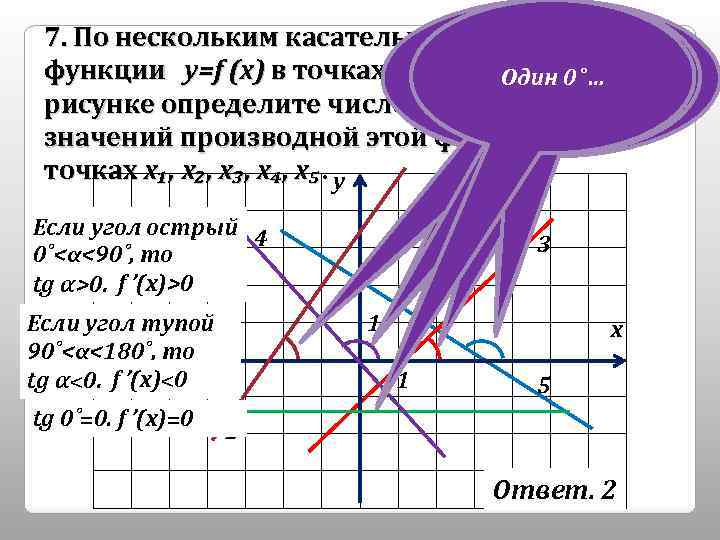Выделим углы 7. По нескольким касательным. Выделимуглы к графику Выделим углы наклона к оси ОХ Определим наклонакк оси ОХ функции у=f (x) в точках х₁, х₂, х₃, Одинкоси ОХ х₄, наклонатупых… наклона 0˚… ОХ Два всех на Два х₅ оси острых… виды углов… всех касательных всех рисунке определите число положительных касательных … … касательных … значений производной этой функции в точках х₁, х₂, х₃, х₄, х₅. у Если угол острый 4 0˚<α<90˚, то tg α>0. f ’(x)>0 Если угол тупой 90˚<α<180˚, то tg α<0. f ’(x)<0 1 tg 0˚=0. f ’(x)=0 3 1 х 1 5 2 Ответ. 2

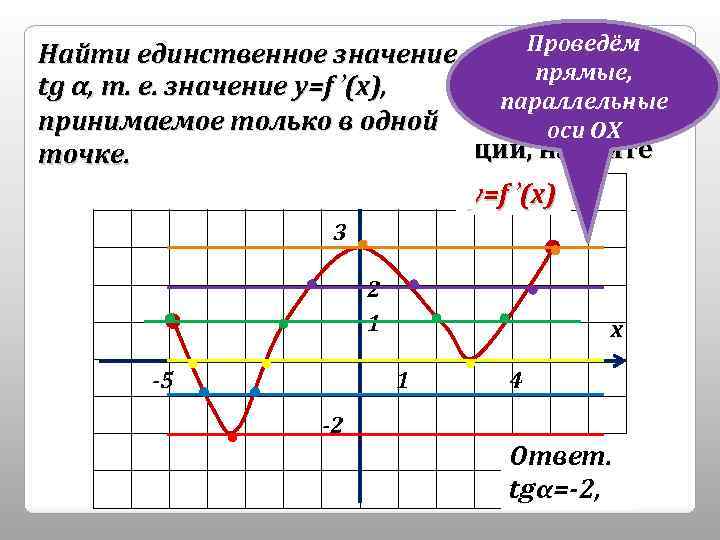Проведём 8. Известно, что существует только одна Найти единственное значение прямые, касательная к графику функции у=f(x), tg α, т. е. значение у=f ’(x), параллельные наклонённая только одной принимаемое к оси ОХвпод углом α. Используя оси ОХ график точке. производной этой функции, найдите у tgα. у=f ’(x) 3 2 1 -5 х 1 4 -2 Ответ. tgα=-2,