V 12 2 p 1

V 12/ 2 + p 1/ + gz 1= V 22/2 + p 2/ + gz 2 + hl. T H E A D L O S S hl. T = hl + hm

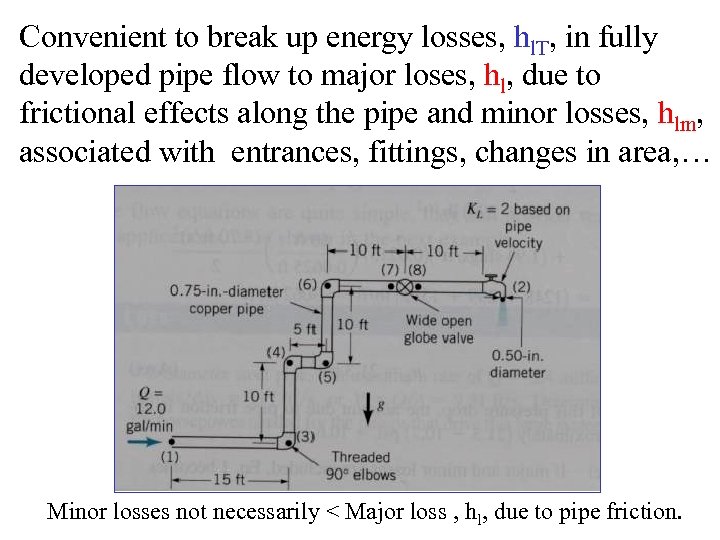Convenient to break up energy losses, hl. T, in fully developed pipe flow to major loses, hl, due to frictional effects along the pipe and minor losses, hlm, associated with entrances, fittings, changes in area, … Minor losses not necessarily < Major loss , hl, due to pipe friction.

Minor losses traditionally calculated as: hlm = KV 2/2 (K for inlets, exits, enlargements and contractions) where K is the loss coefficient or hlm = (Cpi – Cp)V 2/2 (Cpi & Cp for diffusers) where Cp is the pressure recovery coefficient or hlm = f(Le/D)V 2/2 (Le for valves, fittings, pipe bends) where Le is the equivalent length of pipe. Both K and Le must be experimentally determined and will depend on geometry and Re, uavg. D/. At high flow rates weak dependence on Re.

V 1 avg 2/ 2 + p 1/ + gz 1= V 2 avg 2/2 + p 2/ + gz 2 + hl. T = hl + hm; hlm = KV 2/2 inlets, sudden enlargements & contractions; gradual contractions and exits

Minor losses due to inlets: hlm= p/ = K(V 2/2); V 2 = mean velocity in pipe If K=1, p = V 2/2

V 1 avg 2/ 2 + p 1/ + gz 1= V 2 avg 2/2 + p 2/ + gz 2 + hl. T = hl + hm

Head is lost because of viscous dissipation when flow is slowed down (2 -3) and in violent mixing in the separated zones For a sharp entrance ½ of the velocity head is lost at the entrance!

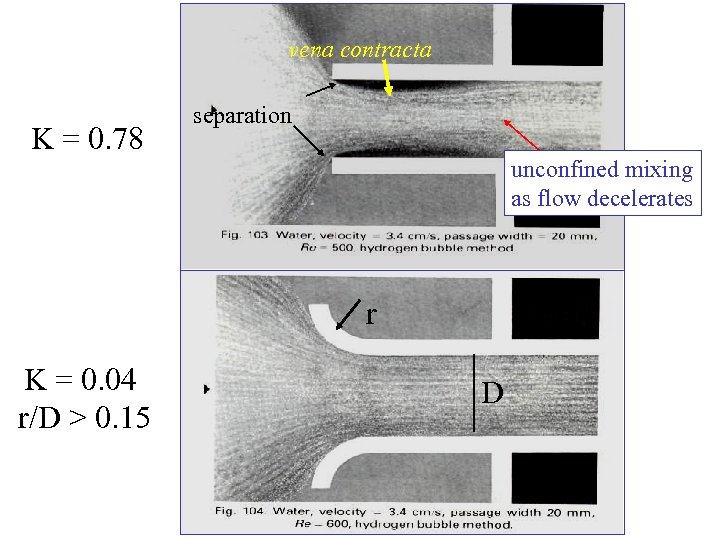vena contracta K = 0. 78 separation unconfined mixing as flow decelerates r K = 0. 04 r/D > 0. 15 D

V 12/ 2 + p 1/ + gz 1= V 22/2 + p 2/ + gz 2 + hl. T = hl + hlm; hlm = KV 2/2 inlets, sudden enlargements & contractions; gradual contractions and exits

Minor losses due to sudden area change: hlm= p/ = K(V 2/2); V 2 = faster mean velocity pipe • hlm head losses are primarily due to separation • Energy is dissipated deceleration after separation leading to violent mixing in the separated zones

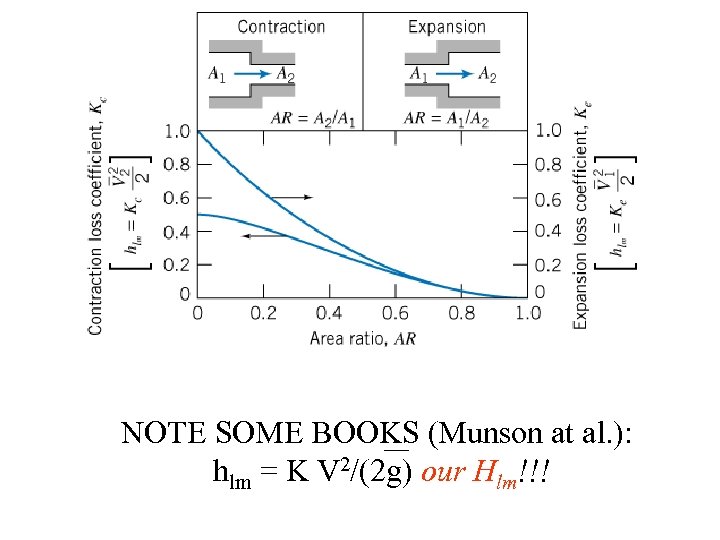NOTE SOME BOOKS (Munson at al. ): hlm = K V 2/(2 g) our Hlm!!!

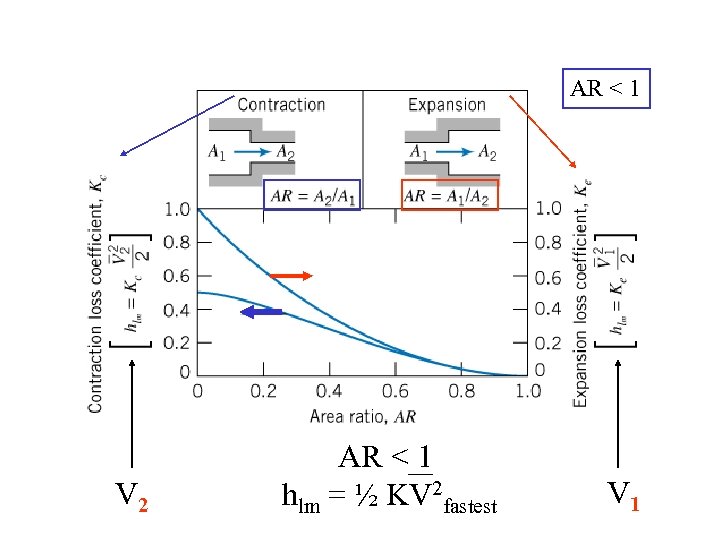AR < 1 V 2 AR < 1 hlm = ½ KV 2 fastest V 1

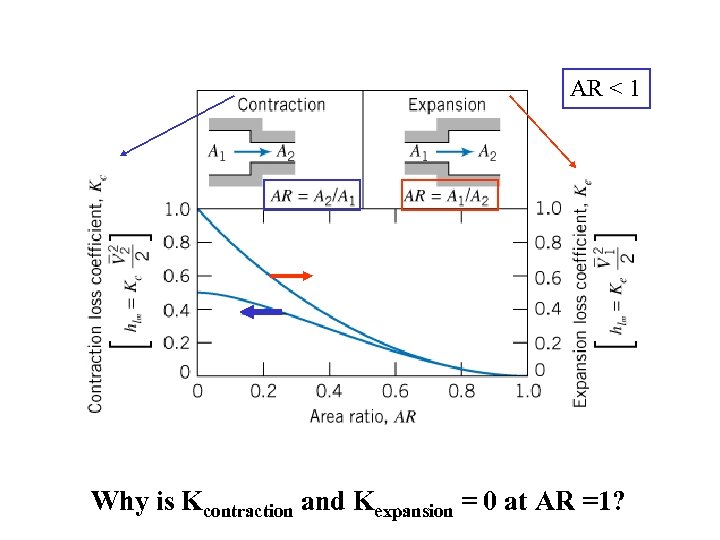AR < 1 Why is Kcontraction and Kexpansion = 0 at AR =1?

V 1 avg 2/ 2 + p 1/ + gz 1= V 2 avg 2/2 + p 2/ + gz 2 + hl. T = hl + hlm; hlm = KV 2/2 inlets, sudden enlargements & contractions; gradual contractions and exits

Entire K. E. of exiting fluid is dissipated through viscous effects, V of exiting fluid eventually = 0 so K = 1, regardless of the exit geometry. hlm = KV 2/2 hydrogen bubbles Only diffuser can help by reducing V. Water, velocity = 14 cm/s, width of opening = 30 mm, Re = 4300

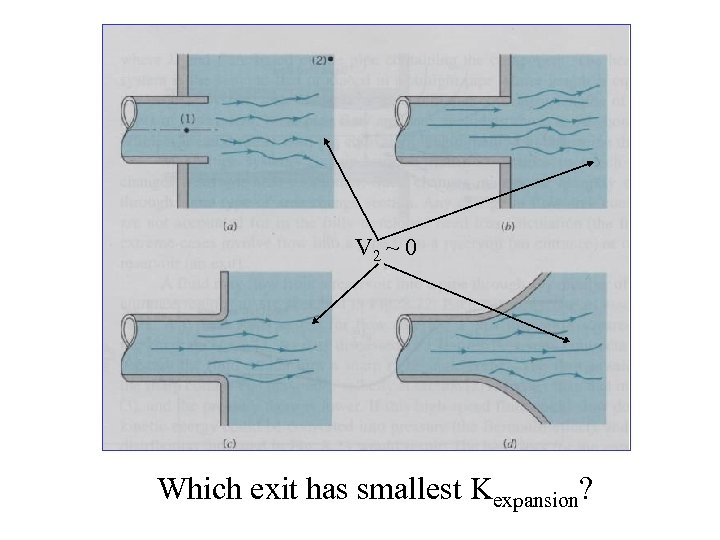V 2 ~ 0 Which exit has smallest Kexpansion?

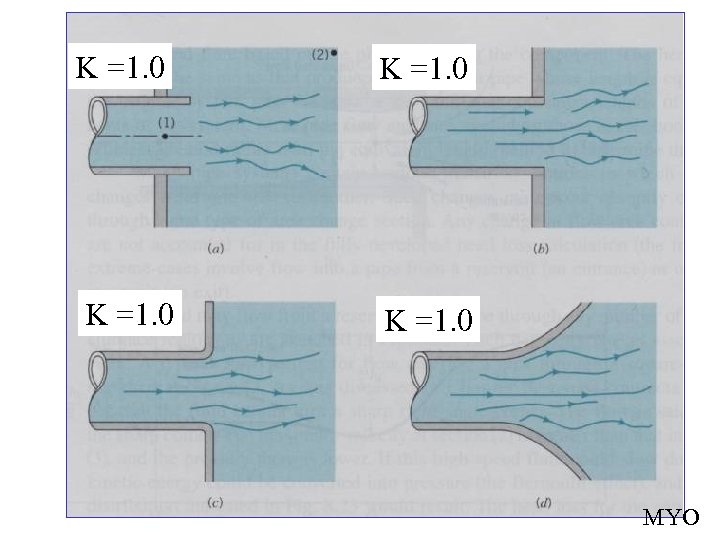K =1. 0 MYO

V 1 avg 2/ 2 + p 1/ + gz 1= V 2 avg 2/2 + p 2/ + gz 2 + hl. T = hl + hlm; hlm = KV 2/2 inlets, sudden enlargements & contractions; gradual contractions and exits

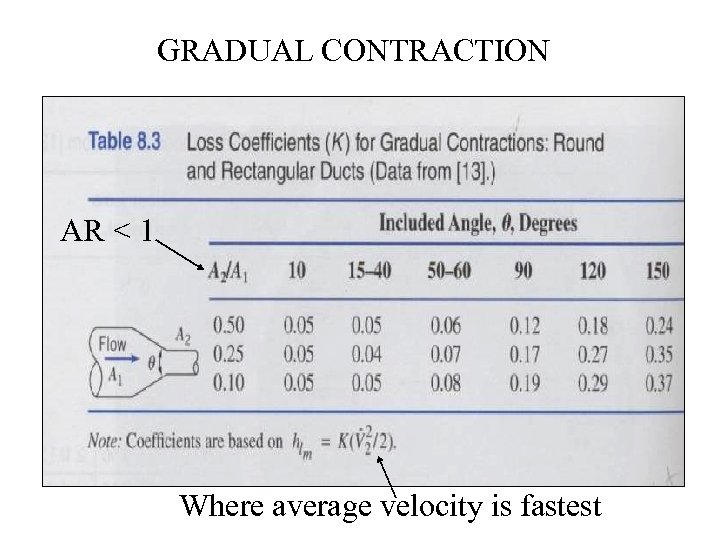GRADUAL CONTRACTION AR < 1 Where average velocity is fastest

breath

V 1 avg 2/ 2 + p 1/ + z 1= V 2 avg 2/2 + p 2/ + gz 2 + hl. T = hl + hlm; hlm = p/ = (Cpi – Cp) 1/2 V 12 gentle expansions ~ diffusers

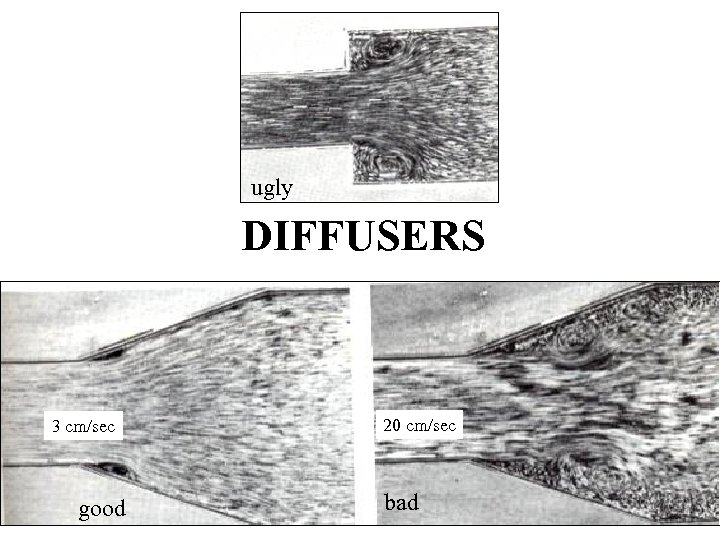ugly DIFFUSERS 3 cm/sec good 20 cm/sec bad

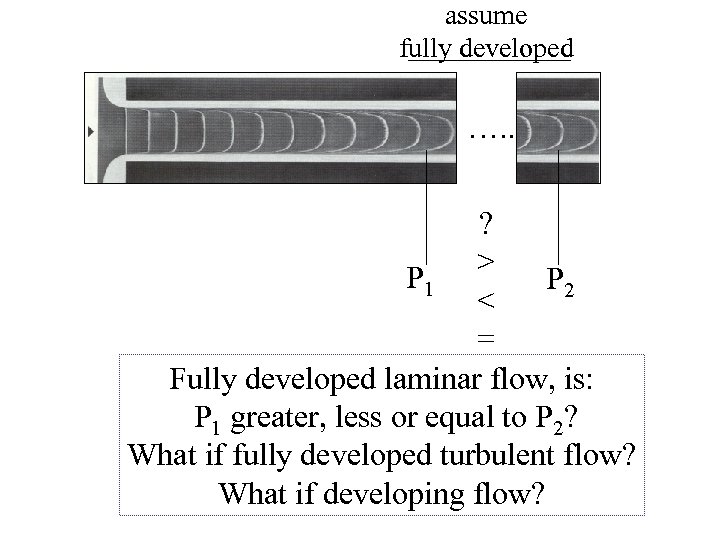assume fully developed …. . ? P 1 > P 2 < = Fully developed laminar flow, is: P 1 greater, less or equal to P 2? What if fully developed turbulent flow? What if developing flow?

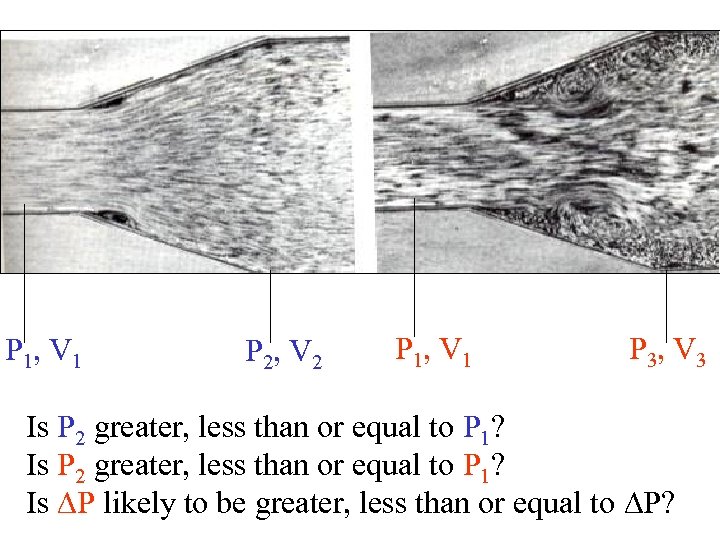P 1, V 1 P 2, V 2 P 1, V 1 P 3, V 3 Is P 2 greater, less than or equal to P 1? Is P likely to be greater, less than or equal to P?

DIFFUSERS Diffuser data usually presented as a pressure recovery coefficient, Cp = (p 2 – p 1) / (1/2 V 12 ) Cp indicates the fraction of inlet K. E. that appears as pressure rise [ hlm = p/ = (Cpi – Cp) 1/2 V 12] The greatest that Cp can be is Cpi, the case of zero friction.

DIFFUSERS Diffuser data usually presented as a pressure recovery coefficient, Cp = (p 2 – p 1) / (1/2 V 12 ) Cp indicates the fraction of inlet K. E. that appears as pressure rise [ hlm = p/ = (Cpi – Cp) 1/2 V 12] Cp will get from empirical data charts. It is not difficult to show that the ideal (frictionless) pressure recovery coefficient is: Cpi = 1 – 1/AR 2, where AR = area ratio

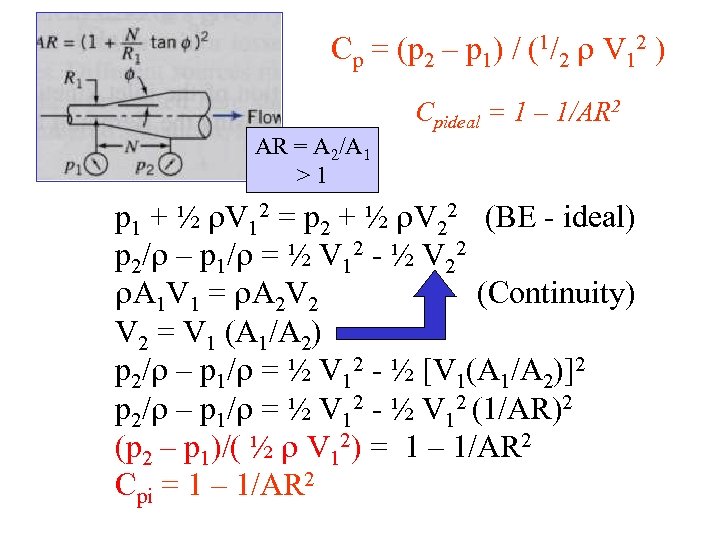Cp = (p 2 – p 1) / (1/2 V 12 ) Cpideal = 1 – 1/AR 2 AR = A 2/A 1 >1 p 1 + ½ V 12 = p 2 + ½ V 22 (BE - ideal) p 2/ – p 1/ = ½ V 12 - ½ V 22 A 1 V 1 = A 2 V 2 (Continuity) V 2 = V 1 (A 1/A 2) p 2/ – p 1/ = ½ V 12 - ½ [V 1(A 1/A 2)]2 p 2/ – p 1/ = ½ V 12 - ½ V 12 (1/AR)2 (p 2 – p 1)/( ½ V 12) = 1 – 1/AR 2 Cpi = 1 – 1/AR 2

Relating Cp to Cpi and hlm p 1 / + ½ V 12 = p 2/ + ½ V 22 + hlm (z 1 = z 2 = 0) hlm = V 12/2 - V 22/2 – (p 2 – p 1)/ hlm = V 12/2 {1 + V 22/V 12 – (p 2 – p 1)/ ( 1/2 V 12)} A 1 V 1 = A 2 V 2 Cp = (p 2 – p 1)/ ( 1/2 V 12) (Cp is positive & < Cpi) hlm = V 12/2 {1 - A 12/A 22 – Cp} Cpi = 1 – 1/AR 2 hlm = V 12/2 {Cpi – Cp} Q. E. D. (see Ex. 8. 10)

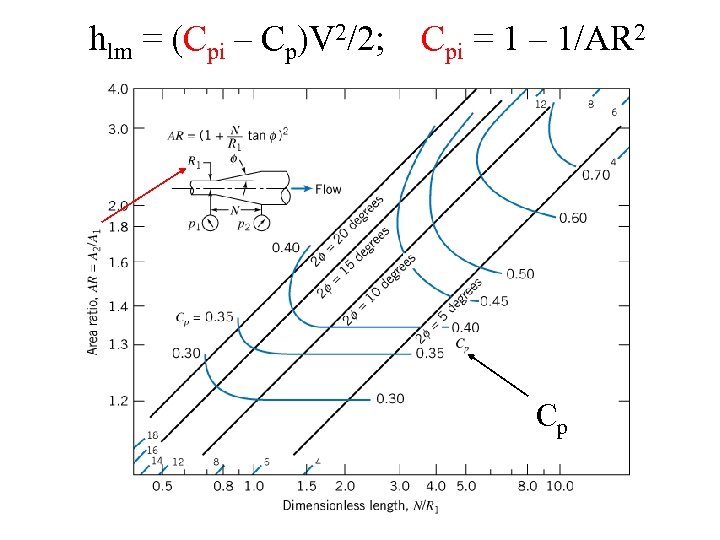hlm = (Cpi – Cp)V 2/2; Cpi = 1 – 1/AR 2 Cp

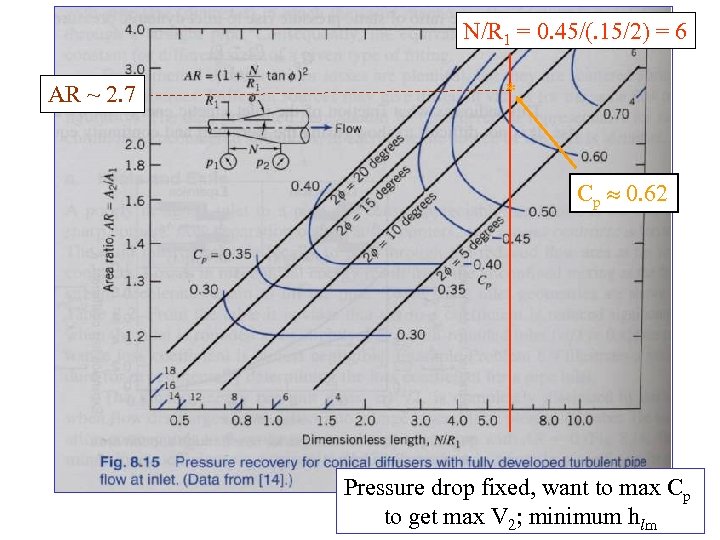N/R 1 = 0. 45/(. 15/2) = 6 AR ~ 2. 7 * Cp 0. 62 Pressure drop fixed, want to max Cp to get max V 2; minimum hlm

If flow too fast or angle too big may get flow separation. Cp for Re > 7. 5 x 104, “essentially” independent of Re

V 1 avg 2/ 2 + p 1/ + z 1= V 2 avg 2/2 + p 2/ + gz 2 + hl. T = hl + hlm; hlm = f(Le/D)V 2/2 valves and fittings

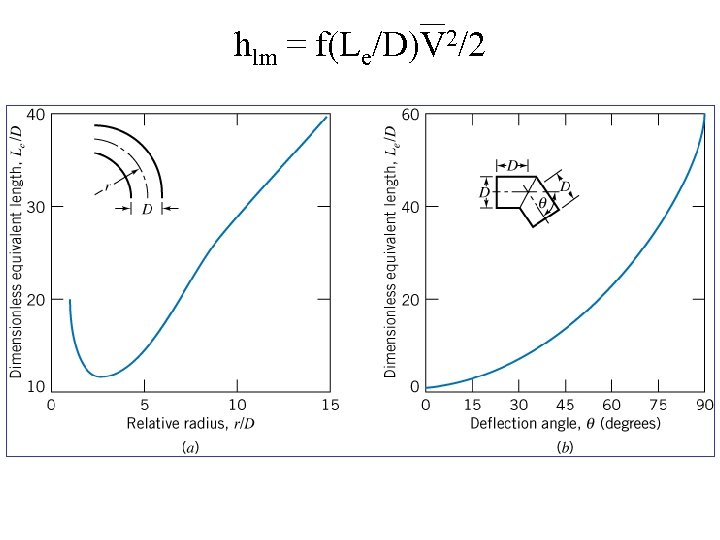hlm = f(Le/D)V 2/2

Head loss of a bend is greater than if pipe was straight (again due to separation).

Nozzle Problem

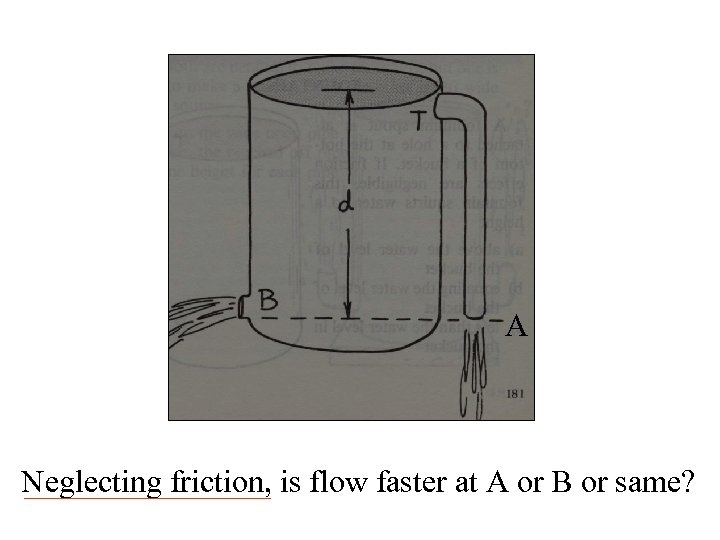A Neglecting friction, is flow faster at A or B or same?

V 12/ 2 + p 1/ + z 1= V 22/2 + p 2/ + gz 2 + hl. T =0 VA 2/ 2 + patm/ + d = VB 2/ 2 + patm/ + d A If flow at B did not equal flow at A then could connect and make perpetual motion machine. A

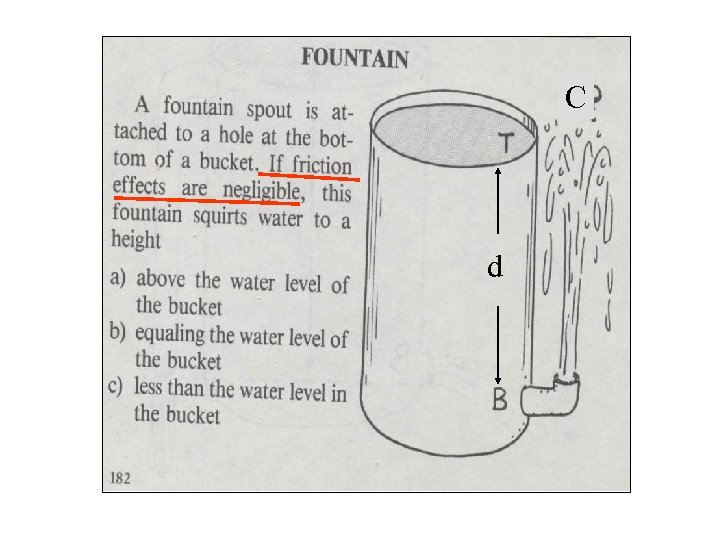C d

C d V 12/ 2 + p 1/ + z 1= V 22/2 + p 2/ + gz 2 + hl. T =0 0 =0 VT 2/ 2 + patm/ + d = VC 2/ 2 + patm/ + d

? neglect friction V 12/ 2 + p 1/ + z 1= V 22/2 + p 2/ + gz 2 + hl. T

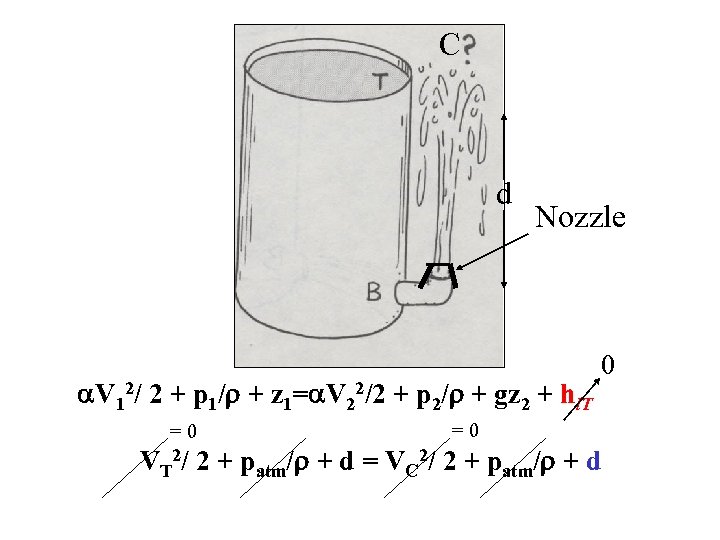C d Nozzle V 12/ 2 + p 1/ + z 1= V 22/2 + p 2/ + gz 2 + hl. T =0 0 =0 VT 2/ 2 + patm/ + d = VC 2/ 2 + patm/ + d

breath

Pipe Flow Examples ~ Solving for pressure drop in horizontal pipe

V 1 avg 2/2 + p 1/ + gz 1 – ( V 2 avg 2/2 + p 2/ + gz 2) = hl. T = hl + hlm = f [L/D][V 2/2] + f [Le/D][V 2/2] + K[V 2/2] Laminar flow ~ f = 64/Re. D Turbulent flow ~ 1/f 0. 5 = -2. 0 log{(e/D)/3. 7 + 2. 51/(Re. D f 0. 5) (f = 0. 316/Re. D 0. 25 for Re < 105) p 2 - p 1 = ? ; Know hl. T , L, D, Q, e, , , z 2, z 1

p 2 - p 1 = ? ; Know L, D, Q, e, , , z 2, z 1 Compute the pressure drop in 200 ft of horizontal 6 -in-diameter asphalted cast-iron pipe carrying water with a mean velocity of 6 ft/s. * V 1 avg 2/2 + p 1/ + gz 1 - V 2 avg 2/2 - p 2/ - gz 2 = f [L/D][V 2/2] + f [Le/D][V 2/2] + K[V 2/2] p 1/ - p 2/ = f [L/D][V 2/2] = hlm

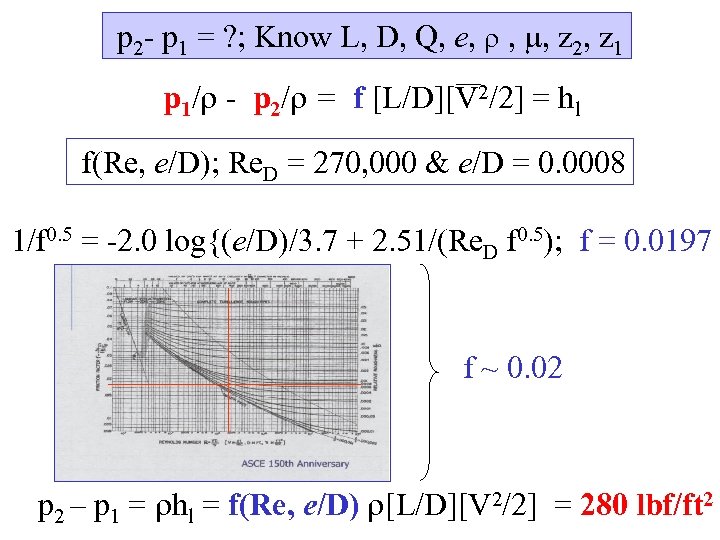p 2 - p 1 = ? ; Know L, D, Q, e, , , z 2, z 1 p 1/ - p 2/ = f [L/D][V 2/2] = hl f(Re, e/D); Re. D = 270, 000 & e/D = 0. 0008 1/f 0. 5 = -2. 0 log{(e/D)/3. 7 + 2. 51/(Re. D f 0. 5); f = 0. 0197 f ~ 0. 02 p 2 – p 1 = hl = f(Re, e/D) [L/D][V 2/2] = 280 lbf/ft 2

Pipe Flow Examples ~ Solving for pressure drop in non-horizontal pipe

p 2 - p 1 = ? ; Know L, D, Q, e, , , z 2, z 1 Oil with = 900 kg/m 3 and = 0. 00001 m 2/s flows at 0. 2 m 3/s through 500 m of 200 mm-diameter cast iron pipe. Determine pressure drop if pipe slopes down at 10 o in flow direction. V 1 avg 2/2 + p 1/ + gz 1 - V 2 avg 2/2 - p 2/ - gz 2 = f [L/D][V 2/2] + f [Le/D][V 2/2] + K[V 2/2] p 1/ + gz 1 - p 2/ - gz 2= f [L/D][V 2/2] = hlm

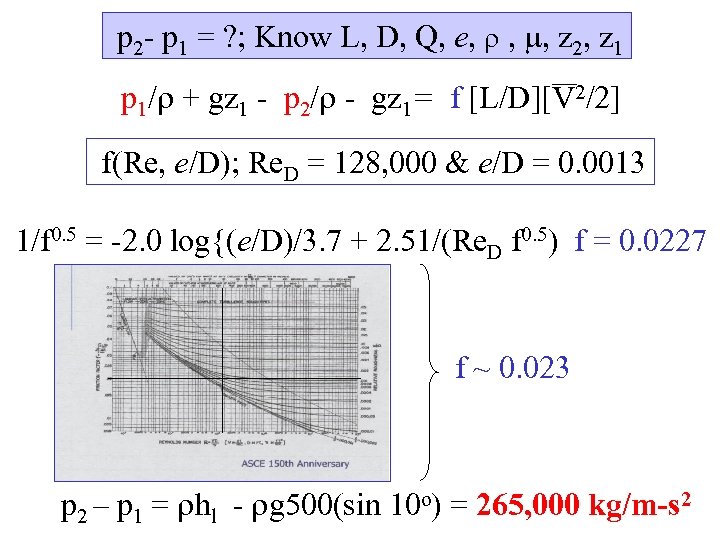p 2 - p 1 = ? ; Know L, D, Q, e, , , z 2, z 1 p 1/ + gz 1 - p 2/ - gz 1= f [L/D][V 2/2] f(Re, e/D); Re. D = 128, 000 & e/D = 0. 0013 1/f 0. 5 = -2. 0 log{(e/D)/3. 7 + 2. 51/(Re. D f 0. 5) f = 0. 0227 f ~ 0. 023 p 2 – p 1 = hl - g 500(sin 10 o) = 265, 000 kg/m-s 2

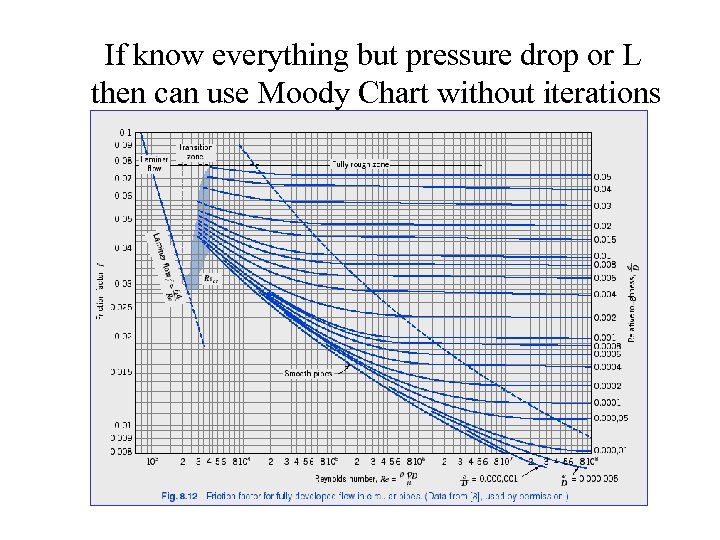If know everything but pressure drop or L then can use Moody Chart without iterations

Pipe Flow Examples ~ Solving for V in horizontal pipe

Q = ? ; Know L, D, Q, e, , , z 2, z 1, p 2 Compute the average velocity in 200 ft of horizontal 6 -in-diameter asphalted cast-iron pipe carrying water with a pressure drop of 280 lbf/ft 2. V 1 avg 2/2 + p 1/ + gz 1 - V 2 avg 2/2 - p 2/ - gz 2 = f [L/D][V 2/2] + f [Le/D][V 2/2] + K[V 2/2] p 1/ - p 2/ = f [L/D][V 2/2]

p 1/ - p 2/ = f [L/D][V 2/2] V = (0. 7245/f) f ~ 0. 19 e/D = 0. 0008 Guess fully rough regime f ~ 0. 19

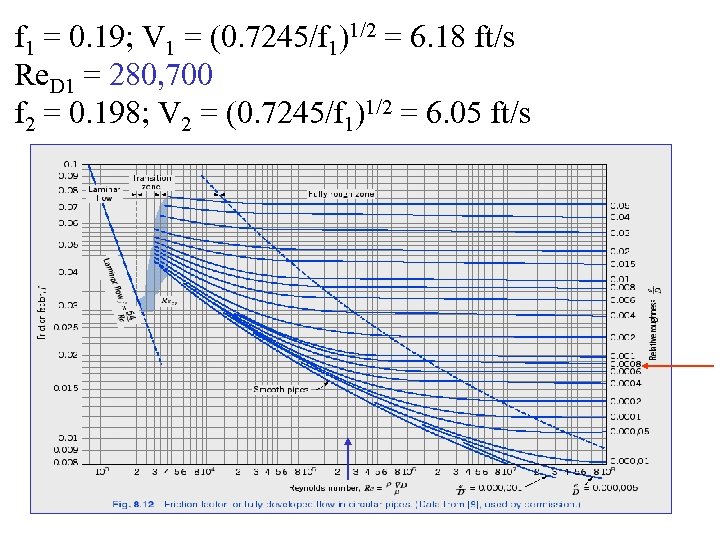f 1 = 0. 19; V 1 = (0. 7245/f 1)1/2 = 6. 18 ft/s Re. D 1 = 280, 700 f 2 = 0. 198; V 2 = (0. 7245/f 1)1/2 = 6. 05 ft/s

Pipe Flow Examples ~ Solving for D in horizontal pipe

Q = ? ; Know L, D, Q, e, , , z 2, z 1, p 2 Compute the diameter of a 200 m of horizontal pipe, e = 0. 0004 mm, carrying 1. 18 ft 3/s, = 0. 000011 ft 2/s and the head loss is 4. 5 ft. Hl. T = hl/g = [length] = 4. 5 ft V 1 avg 2/2 g + p 1/ g + z 1 - V 2 avg 2/2 g - p 2/ g - z 2 = f [L/D][V 2/2 g] + f [Le/D][V 2/2 g] + K[V 2/2 g] p 1/ - p 2/ = f [L/D][V 2/2] f = function of Re. D and e/D

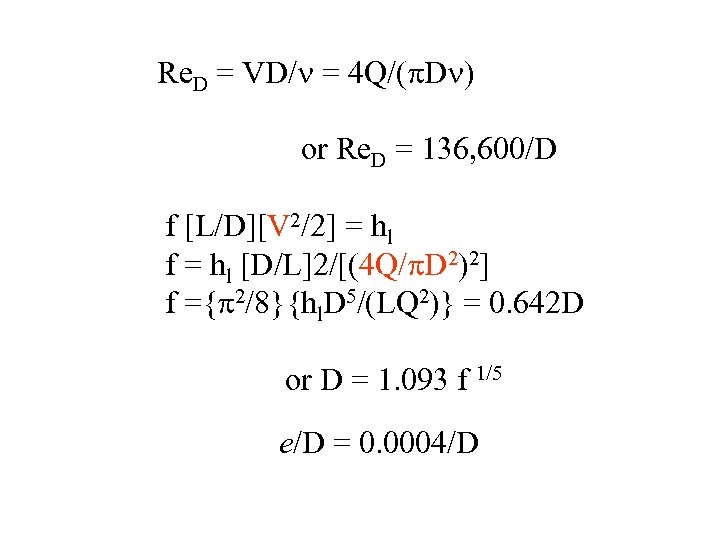Re. D = VD/ = 4 Q/( D ) or Re. D = 136, 600/D f [L/D][V 2/2] = hl f = hl [D/L]2/[(4 Q/ D 2)2] f ={ 2/8}{hl. D 5/(LQ 2)} = 0. 642 D or D = 1. 093 f 1/5 e/D = 0. 0004/D

(1) Re. D = 136, 600/D (2) D = 1. 093 f 1/5 (3) e/D = 0. 0004/D Guess f ~ 0. 03; then from (2) get D ~ 1. 093(0. 03)1/5 ~ 0. 542 ft From (1) get Re. D ~ 136, 600/0. 542 ~ 252, 000 From (3) get e/D = 0. 0004/0. 542 ~ 7. 38 x 10 -4 fnew ~ 0. 0196 from plot; Re. Dnew ~274, 000; fnewest ~ 0. 0198 from plot Dnew ~ 0. 498; e/D ~8. 03 x 10 -4 Dnewest~ 0. 499

Solve for V in vertical pipe with minor losses, hlm

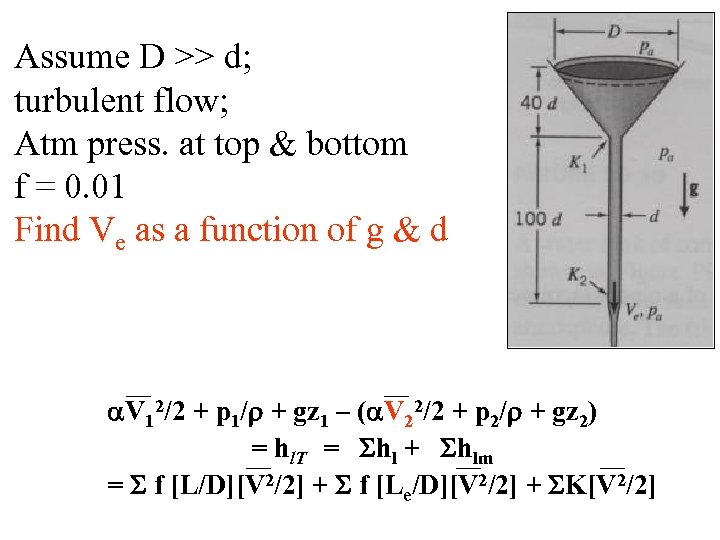Assume D >> d; turbulent flow; Atm press. at top & bottom f = 0. 01 Find Ve as a function of g & d V 12/2 + p 1/ + gz 1 – ( V 22/2 + p 2/ + gz 2) = hl. T = hl + hlm = f [L/D][V 2/2] + f [Le/D][V 2/2] + K[V 2/2]

V 12/2 + p 1/ + gz 1 – ( V 22/2 + p 2/ + gz 2) = hl. T = hl + hlm = f [L/D][V 2/2] + f [Le/D][V 2/2] + K[V 2/2] V 02/2 + patm/ + gz 0 - V 22/2 - patm/ - gz 2 = f [L/D](V 22/2)+(K 1+K 2+f[L/d])(V 22/2) V 02/2 = 0; V 22/2 = 1 V 22/2 gz 0–gz 2–V 22/2={f [L/D]+K 1+K 2)}(V 22/2) V 22 = 2 g(z 0 -z 2)/[1 + K 2 + f(L/d)] V 22 =2 g 140 d/(1+0. 5+1. 0+001 x 100)1/2 V 2 = (80 gd)1/2

laminar transitional turbulent

The END ~