ÚVOD DO TESTOVÁNÍ STATISTICKÝCH HYPOTÉZ Příklad V

ÚVOD DO TESTOVÁNÍ STATISTICKÝCH HYPOTÉZ

Příklad V rámci pokusu, který proběhl na univerzitě v Mississippi, byli studenti požádáni, aby reagovali na stimul v podobě rozsvícení červeného světla. Pokusu se zúčastnilo 12 chlapců a 10 dívek, pro každého byla zaznamenána doba reakce v sekundách. Liší se doba reakce u dívek a chlapců?

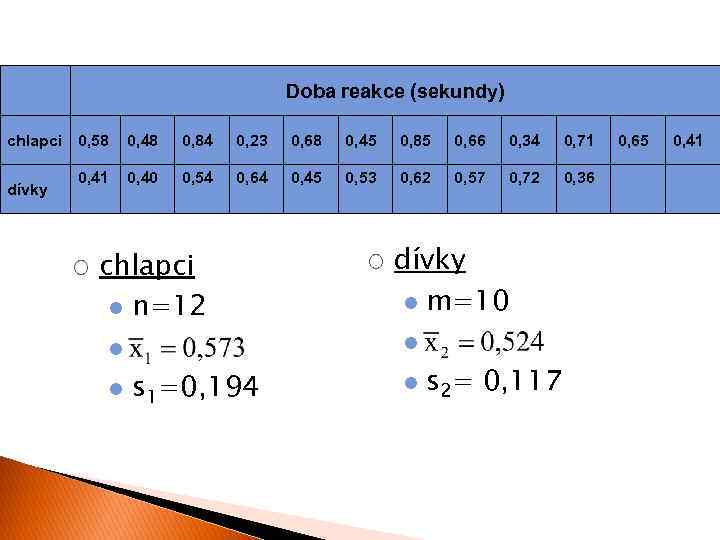Doba reakce (sekundy) chlapci 0, 58 0, 48 0, 84 0, 23 0, 68 0, 45 0, 85 0, 66 0, 34 0, 71 0, 40 0, 54 0, 64 0, 45 0, 53 0, 62 0, 57 0, 72 0, 36 dívky ¡ chlapci l n=12 dívky l m=10 l l l ¡ s 1=0, 194 l s 2= 0, 117 0, 65 0, 41

μ 2 μ 1=μ 2 ? ? ? μ 1≠μ 2

Testování hypotéz H 0: μ 1=μ 2 H 1: μ 1≠μ 2 H 1: μ 1>μ 2 H 1: μ 1<μ 2 nulová hypotéza alternativní hypotéza oboustranná jednostranná nulová hypotéza ◦ vždy tvrzení o shodě (rovnosti) ◦ není rozdíl v průměrné reakci chlapců a dívek ◦ váha balení mouky se v průměru neliší od tvrzení výrobce

statistická hypotéza – tvrzení o parametrech rozdělení nebo jeho tvaru statistický test využití informace ve výběrových datech pro vyslovení závěru o H 0 testová statistika (testové kriterium) charakterizuje stupeň nesouladu mezi tvrzením nulové hypotézy a pozorováním (naměřenými daty)

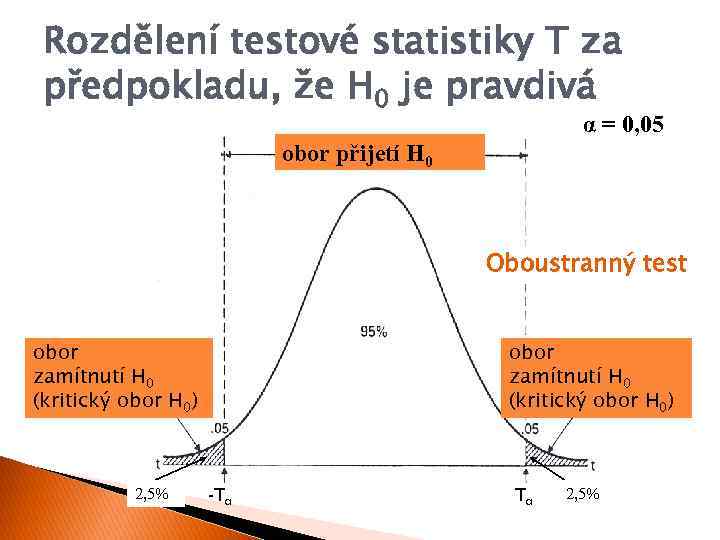Rozdělení testové statistiky T za předpokladu, že H 0 je pravdivá α = 0, 05 obor přijetí H 0 Oboustranný test obor zamítnutí H 0 (kritický obor H 0) 2, 5% obor zamítnutí H 0 (kritický obor H 0) -Tα Tα 2, 5%

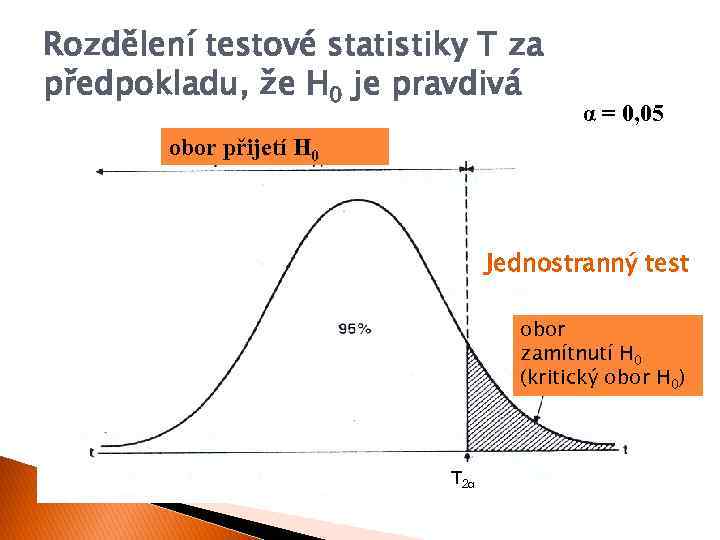Rozdělení testové statistiky T za předpokladu, že H 0 je pravdivá α = 0, 05 obor přijetí H 0 Jednostranný test obor zamítnutí H 0 (kritický obor H 0) T 2α

Rozhodovací pravidlo (oboustranný test) Tα… kritická hodnota pro hladinu významnosti α zamítneme H 0 na hladině významnosti α ve prospěch H 1 H 0 nelze na hladině významnosti α zamítnout

Alternativní způsob (při využití statistického SW) rozhodnutí založeno na p-hodnotě pravděpodobnost hodnoty T za předpokladu, že H 0 platí p<α → zamítneme H 0 na α p>α → nezamítneme H 0 na α

chyba 1. druhu zamítnutí správné nulové hypotézy Ø ppst chyby 1. druhu - hladina významnosti α chyba 2. druhu přijetí nesprávné nulové hypotézy Øppst chyby 2. druhu - β síla testu (1 - β ) – ppst zamítnutí nesprávné nulové hypotézy

závěr testu (rozhodnutí) přijmout H 0 zamítnout H 0 realita H 0 platí H 0 neplatí Při testu volíme hladinu významnosti α, touto volbou ovlivňujeme současně i ppst β.

Postup při statistickém testu 1) Formulace nulové a alternativní hypotézy H 0 a H 1 2) Volba hladiny významnosti α 3) Volba vhodné testové statistiky T 4) Výpočet testového kriteria T na základě výběrových dat 5) Vymezení kritického oboru K pro platnost nulové hypotézy H 0 (resp. výpočet p-hodnoty) 6) Rozhodnutí: 7) Interpretace statistického rozhodnutí T leží v kritickém oboru K (resp. p < α ) → zamítnutí H 0 T neleží v K (resp. p > α ) → H 0 se nezamítá