Utrecht University Classical Cellular Automata and Quantum Field

Utrecht University Classical Cellular Automata and Quantum Field Theory Gerard ’t Hooft Gell-Mann Colloquium Singapore, February 24, 2010

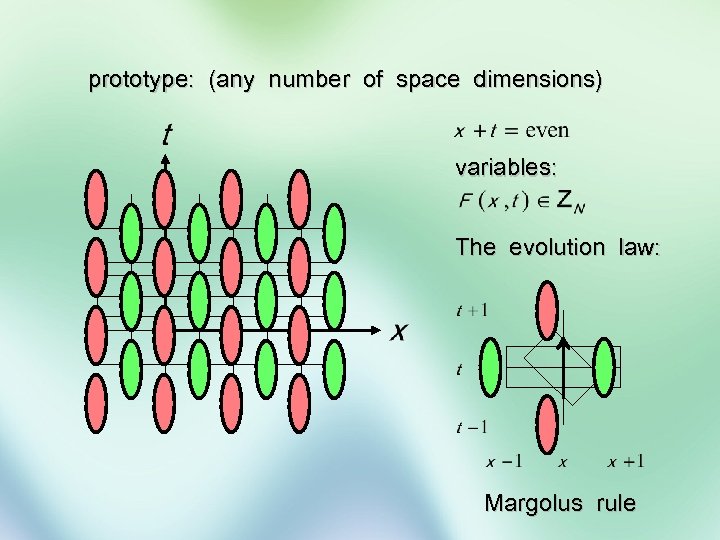prototype: (any number of space dimensions) variables: The evolution law: Margolus rule

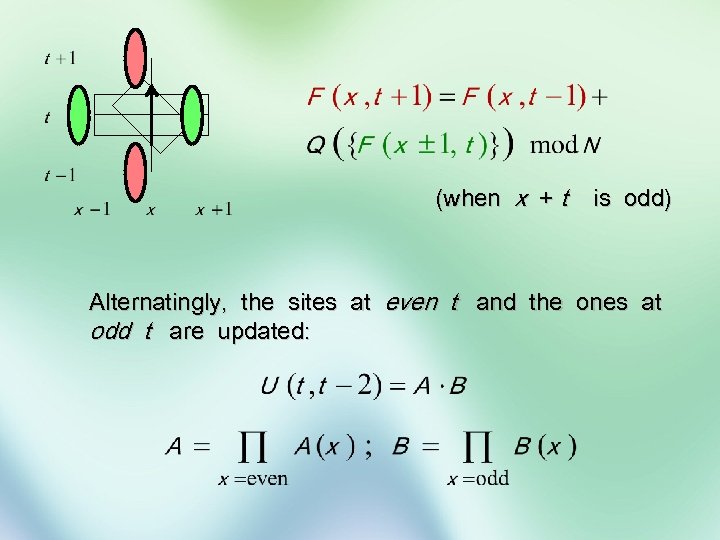(when x + t is odd) Alternatingly, the sites at even t and the ones at odd t are updated:

A and B are operators. Write them as is the permutation operator for the variable F equal-time commutators:

Write: What is H ? Use Baker-Campbell-Hausdorff:

Faster convergence is reached if we limit ourselves to the conjugation class of H : Where F is chosen such that Write repeated commutators, for instance as: , to find

only if one may terminate a appears to be the perfectly local, bounded BCH series quantum operator, similar to the Hamilton density operator of a QFT. But does the Baker-Campbell-Hausdorff expansion converge ? similarly: stays outside the “light cone”: information does not spread faster than velocity v =1=c as an operator, is (practically) bounded (from below and above), so H should have a lowest eigenstate. This is the vacuum state of the cellular automaton.

But does the Baker-Campbell-Hausdorff expansion converge ? One can argue that divergence occurs when two energy eigenvalues of H are considered that are apart. lanck “P ? rgy” ene

Qu: time translation invariance only strictly holds for time tranlations over integral multiples of Δt , the lattice time unit. Is conservation of energy violated by multiples of ? A 1: yes, if you introduce a classical perturbation: allow the cellular automaton to be perturbed: Then, acts with the beat of the lattice clock. It only respects energy conservation modulo.

A 2: no, if you expand the complete Hamiltonian H into a linearlized part and an interaction piece . The total energy, defined by is exactly conserved. Can one resum the BCH series ?

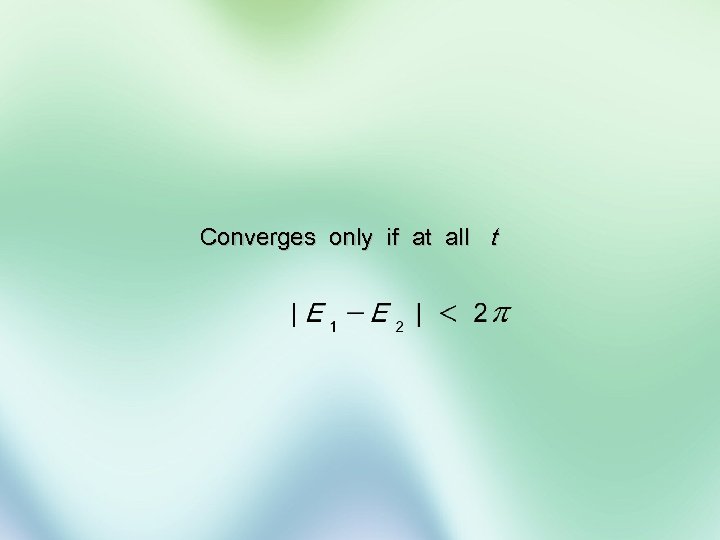Converges only if at all t

This distinction may be of crucial importance for the following discussion:

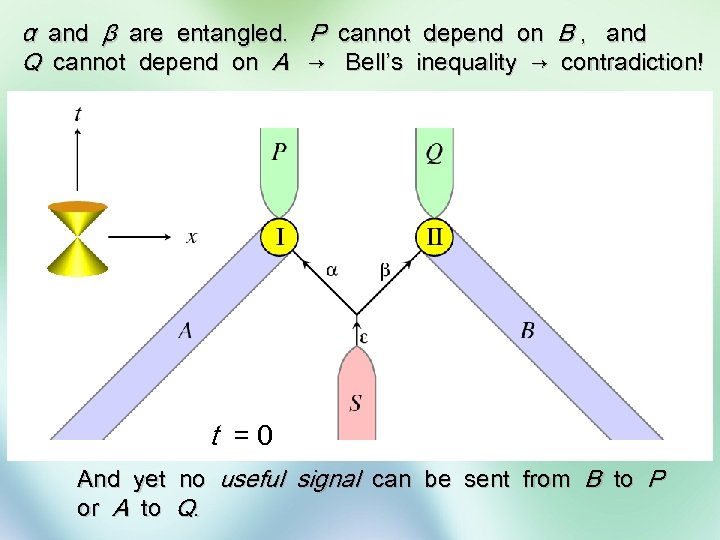α and β are entangled. P cannot depend on B , and Q cannot depend on A → Bell’s inequality → contradiction! t =0 And yet or A to no useful signal can be sent from B to P Q.

It is essential to realize that Bell’s inequalities refer to the states a system is in, whereas our “hidden variables” are a theory for their dynamics. We can always assume our system to be in a state violating Bell’s inequalities, and evolve it backwards in time, to conclude that the initial state must have been a thoroughly entangled one. The Universe or rather, our understanding of it, must have started out as a highly entangled state … But so what ?

Our world is not quantum mechanical, but only our perception of it …

G. ‘t H, ar. Xiv: 0909. 3426; P. Jizba, H. Kleinert, F. Scardigli, ar. Xiv: 012. 2253, And others …

The Cellular Automaton Prototype Its evolution operator Hamilton formalism Convergence problem QM and GR Conclusion