logic.ppt
- Количество слайдов: 34


УСТРОЙСТВА ОБРАБОТКИ ИНФОРМАЦИИ И УПРАВЛЯЮЩИЕ УСТРОЙСТВА. ОСНОВНЫМ УСТРОЙСТВОМ ОБРАБОТКИ ИНФОРМАЦИИ В ЭВМ ЯВЛЯЕТСЯ АРИФМЕТИКО-ЛОГИЧЕСКОЕ УСТРОЙСТВО (АЛУ). ЕГО ОСНОВОЙ является электронная схема, составленная из большого числа транзисторов, называемая СУММАТОРОМ выполняются простейшие логические и арифметические операции над данными, представленными в виде двоичных кодов (НУЛЕЙ И ЕДИНИЦ). В СОВРЕМЕННЫХ ЭВМ АЛУ ОБЪЕДИНЯЕТСЯ С УПРАВЛЯЮЩИМИ УСТРОЙСТВАМИ В ЕДИНУЮ СХЕМУ - ПРОЦЕССОР.
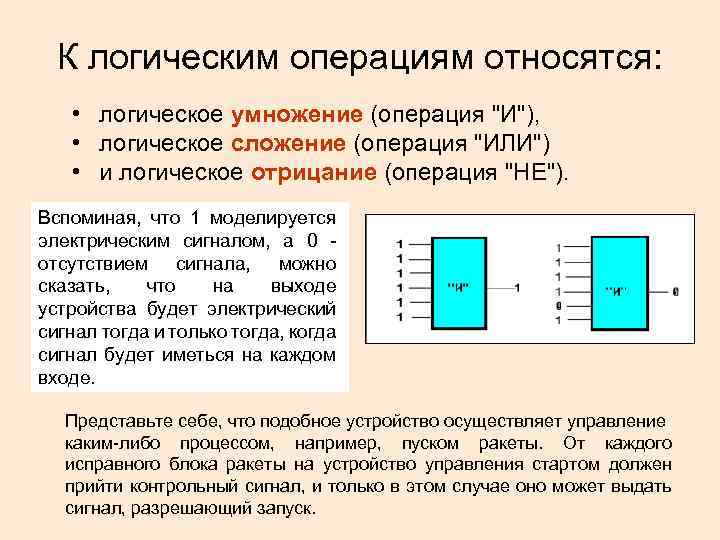
К логическим операциям относятся: • логическое умножение (операция "И"), • логическое сложение (операция "ИЛИ") • и логическое отрицание (операция "НЕ"). Результатом 1 опер. логич. Вспоминая, что моделируется электрическим сигналом, а 01, умножения является отсутствием сигнала, можно если все на исходные сказать, что выходе переменные равны 1, и 0, устройства будет электрический сигналхотя и только тогда, когда если тогда бы одна из них сигнал будет иметься на каждом равна 0. входе. Представьте себе, что подобное устройство осуществляет управление каким-либо процессом, например, пуском ракеты. От каждого исправного блока ракеты на устройство управления стартом должен прийти контрольный сигнал, и только в этом случае оно может выдать сигнал, разрешающий запуск.
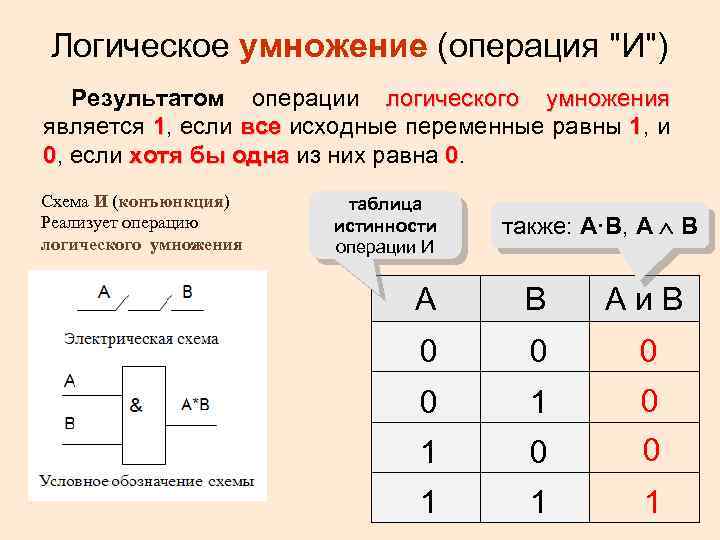
Логическое умножение (операция "И") Результатом операции логического умножения является 1, если все исходные переменные равны 1, и 0, если хотя бы одна из них равна 0. Схема И (конъюнкция) Реализует операцию логического умножения таблица истинности операции И также: A·B, A B A B Аи. B 0 0 1 1 1

Логическое сложение (операция "ИЛИ") Результатом операции логического сложения является 0, если все исходные переменные равны 0, и 1, если хотя бы одна из них равна 1. Схема ИЛИ (дизъюнкция) Реализует операцию логического сложения таблица истинности операции ИЛИ также: A+B, A B A B А или B 0 0 1 1 1 0 1 1

Логическое отрицание (операция "НЕ") Результатом операции логического отрицания является 1, если на входе - 0, и 0, если на входе - 1. Схема НЕ (инвертор) Реализует операцию отрицания также: А не А 0 1 1 0 таблица истинности операции НЕ

На основе этих трёх операций можно производить арифметические действия над числами, представленными в виде нулей и единиц. Теоретической основой для этого являются законы, разработанные еще в 1847 году ирландским математиком Джорджем Булем, Булем известные как Булева алгебра, которая оперирует с логическими переменными, которые могут принимать только два значения: истина или ложь, обозначаемые ложь соответственно 1 и 0. Джордж Буль

Основы алгебры логики Алгебра логики изучает методы установления истинности или ложности высказываний (утверждений). Логический подход заключается в том, что истинность высказываний устанавливается на основании истинности других высказываний, с помощью рассуждений и нахождения противоречий. Основные разделы логики: формальная логика (изучает особенности человеческих рассуждений); • математическая логика (изучает технику математических теорий и доказательств); • диалектическая логика (изучает закономерности и процессы, происходящие в природе, обществе и сознании); • компьютерная логика (логические закономерности применительно к вычислительной технике). •

Логические элементы компьютера Ранее считалось, что работы Буля никому не нужны, и их автор подвергался насмешкам. Однако, в 1938 году американский инженер Клод Шеннон положил Булеву алгебру в основу теории электрических и электронных переключательных схем сумматоров, сумматоров создание которых и привело к появлению ЭВМ, способных автоматически производить арифметические вычисления. ВСЕ ОСТАЛЬНЫЕ ОПЕРАЦИИ, ПРОИЗВОДИМЫЕ ЭВМ, СВОДЯТСЯ К БОЛЬШОМУ ЧИСЛУ ПРОСТЕЙШИХ АРИФМЕТИЧЕСКИХ И ЛОГИЧЕСКИХ ОПЕРАЦИЙ, аналогично тому, как операцию умножения можно свести к большому числу операций сложения. Основные логические операции: И, ИЛИ, НЕ, И–НЕ, ИЛИ–НЕ и др. , выполняемые над двоичными переменными, реализованы в логических схемах.

Основы алгебры логики Основной системой счисления ЭВМ является двоичная СС, в которой также используются только две цифры: 1 и 0. Таким образом, одни и те же цифровые устройства ЭВМ могут применяться для обработки как числовой информации в двоичной СС, так и логических переменных. Это обуславливает универсальность (однотипность) схемной реализации процесса обработки информации в ЭВМ. Алгебра логики – это раздел математической логики, значения всех элементов которой определены в двухэлементном множестве: 0 или 1. Алгебра логики создана для решения логических задач алгебраическими методами.

Высказывание Алгебра логики оперирует с логическими высказываниями. Высказывание – это любое предложение, в отношении которого имеет смысл утверждение о его истинности или ложности. При этом считается, что высказывание удовлетворяет закону исключённого третьего, т. е. каждое высказывание или истинно, или ложно и не может быть одновременно и истинным, и ложным. В алгебре логики все высказывания обозначают буквами: A, B, C и т. д.

Итог : Булева алгебра Двоичное кодирование – все виды информации кодируются с помощью 0 и 1. Задача – разработать оптимальные правила обработки таких данных. Джордж Буль разработал основы алгебры, в которой используются только 0 и 1 (алгебра логики, булева алгебра). Почему "логика"? Результат выполнения операции можно представить как истинность (1) или ложность (0) некоторого высказывания.

Логические высказывания Логическое высказывание – это повествовательное предложение, относительно которого можно однозначно сказать, истинно оно или ложно. Высказывание или нет? q Сейчас идет дождь. q Жирафы летят на север. q История – интересный предмет. q У квадрата – 10 сторон и все разные. q Красиво! q В городе N живут 2 миллиона человек. q Который час?

Обозначение высказываний A – Сейчас идет дождь. B – Форточка открыта. ! простые высказывания (элементарные) Любое высказывание может быть ложно (0) или истинно (1). Составные высказывания строятся из простых с помощью логических связок (операций) "и", "или", "не", "если … то", "тогда и только тогда" и др. Aи. B A или не B если A, то B не A и B A тогда и только тогда, когда B Сейчас идет дождь и открыта форточка. Сейчас идет дождь или форточка закрыта. Если сейчас идет дождь, то форточка открыта. Сейчас нет дождя и форточка открыта. Дождь идет тогда и только тогда, когда открыта форточка.

15 Базовый набор операций С помощью операций И, ИЛИ и НЕ можно реализовать любую логическую функцию. И ИЛИ НЕ базовый набор операций Логическая функция F – это алгебраическое выражение, содержащее элементы алгебры логики A, B, C …, связанные между собой знаками операций, и имеющее возможность принимать только два значения логический 0 или логическую 1. Например, F (a, b, c) = a + a ∗b ∗ c + a +c. Любая Логическая функция может быть задана с помощью таблицы истинности. В левой части которой записываются наборы аргументов, а в правой соответствующее значение функции.

Таблица истинности логического выражения Х – это таблица, где в левой части записываются все возможные комбинации значений исходных данных, а в правой – значение выражения Х для каждой комбинации. На вход электрической схемы поступает двоичный сигнал, связь между ним и выходным сигналом выражается с помощью таблиц истинности. Простая электрическая схема, состоящая из одного и более контактов иллюстрирует работу логической схемы. Значениям 1 и 0 соответствует наличие или отсутствие тока в цепи.
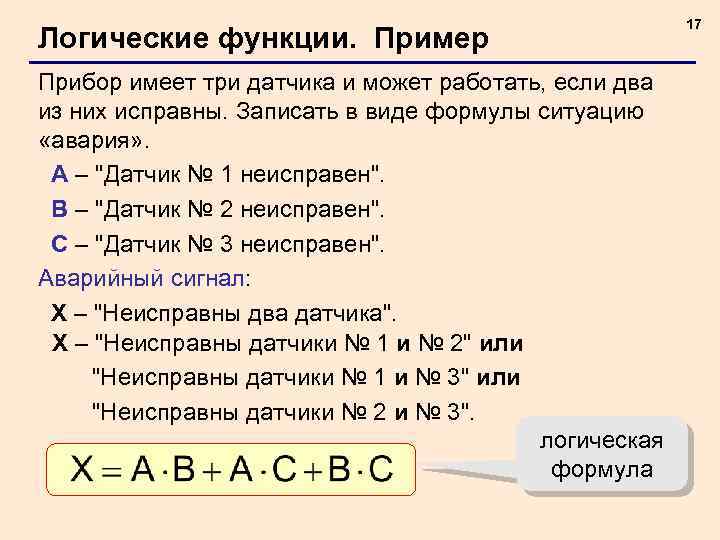
Логические функции. Пример Прибор имеет три датчика и может работать, если два из них исправны. Записать в виде формулы ситуацию «авария» . A – "Датчик № 1 неисправен". B – "Датчик № 2 неисправен". C – "Датчик № 3 неисправен". Аварийный сигнал: X – "Неисправны два датчика". X – "Неисправны датчики № 1 и № 2" или "Неисправны датчики № 1 и № 3" или "Неисправны датчики № 2 и № 3". логическая формула 17
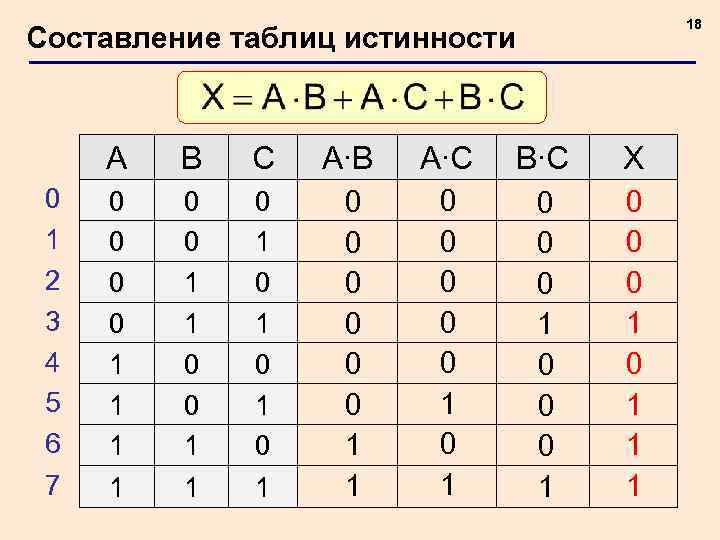
18 Составление таблиц истинности A 0 1 2 3 4 5 6 7 B C A∙B A∙C B∙C X 0 0 1 1 0 1 0 1 0 0 0 1 0 0 0 1 1 1
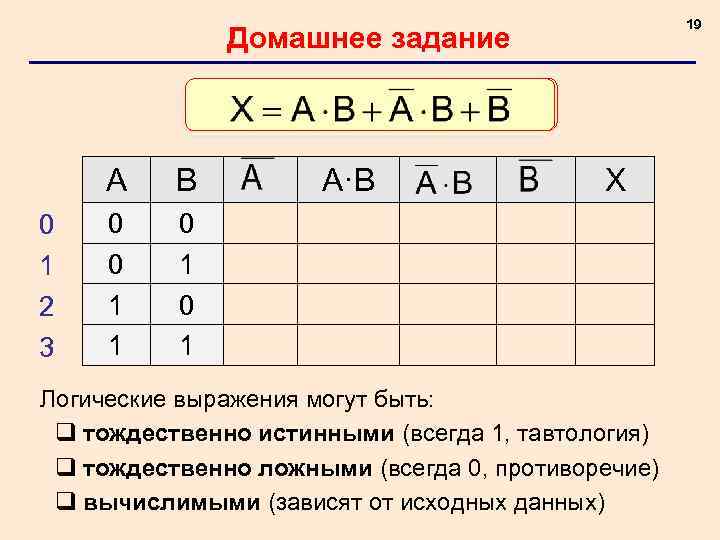
19 Домашнее задание A 0 1 2 3 B 0 0 1 1 A·B X 0 1 Логические выражения могут быть: q тождественно истинными (всегда 1, тавтология) q тождественно ложными (всегда 0, противоречие) q вычислимыми (зависят от исходных данных)

20 Законы алгебры логики

Законы алгебры логики Правила выполнения операций в алгебре логики определяются рядом аксиом, теорем и следствий.
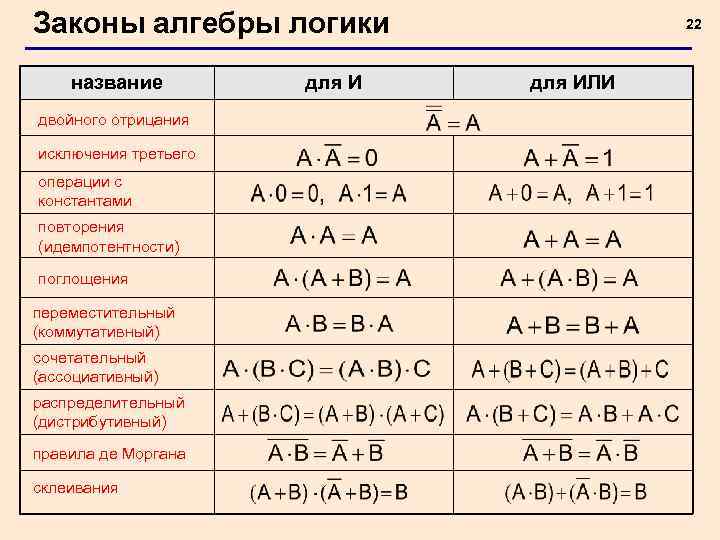
Законы алгебры логики название двойного отрицания исключения третьего операции с константами повторения (идемпотентности) поглощения переместительный (коммутативный) сочетательный (ассоциативный) распределительный (дистрибутивный) правила де Моргана склеивания для И 22 для ИЛИ

23 Логические элементы компьютера
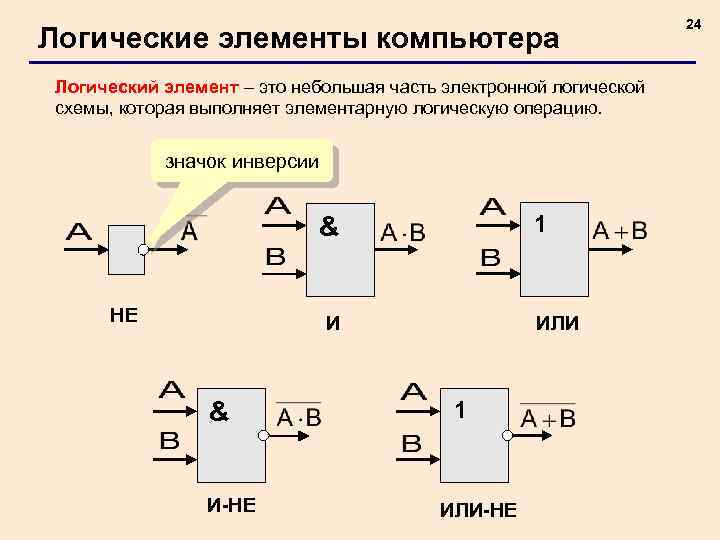
Логические элементы компьютера Логический элемент – это небольшая часть электронной логической схемы, которая выполняет элементарную логическую операцию. значок инверсии 1 & НЕ И & И-НЕ ИЛИ 1 ИЛИ-НЕ 24
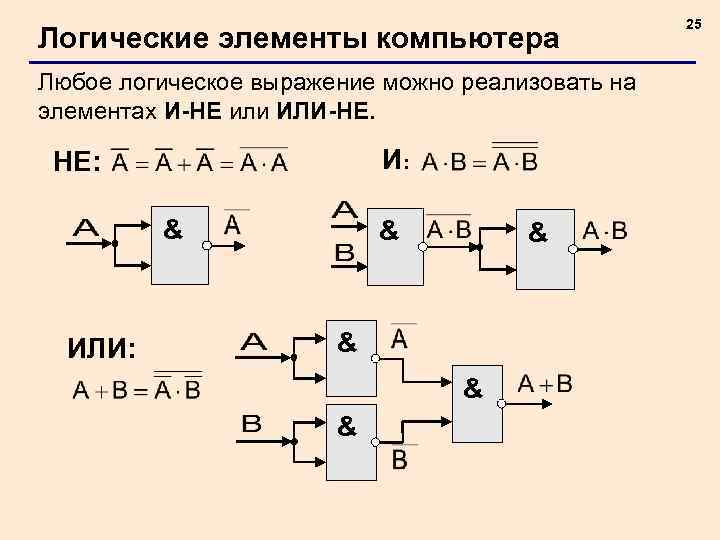
Логические элементы компьютера Любое логическое выражение можно реализовать на элементах И-НЕ или ИЛИ-НЕ. И: НЕ: & ИЛИ: & & & 25
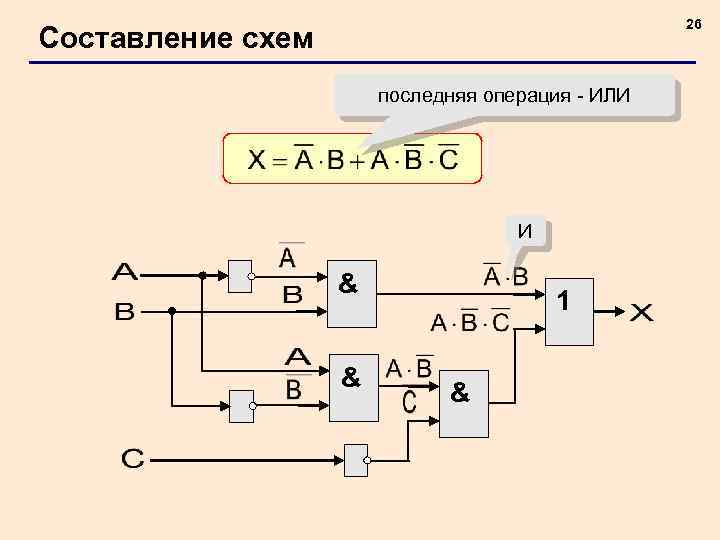
26 Составление схем последняя операция - ИЛИ И & & 1 &
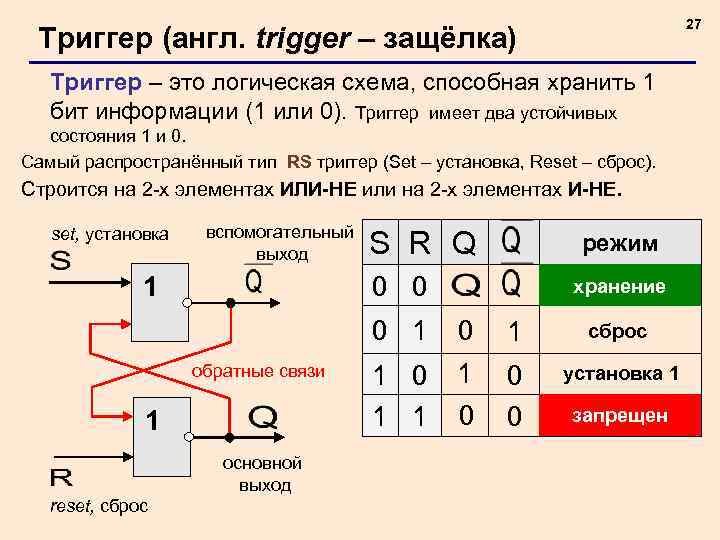
27 Триггер (англ. trigger – защёлка) Триггер – это логическая схема, способная хранить 1 бит информации (1 или 0). Триггер имеет два устойчивых состояния 1 и 0. Самый распространённый тип RS триггер (Set – установка, Reset – сброс). Строится на 2 -х элементах ИЛИ-НЕ или на 2 -х элементах И-НЕ. set, установка вспомогательный выход S R Q режим 0 0 1 хранение 0 1 обратные связи 1 основной выход reset, сброс 0 1 сброс 1 0 1 1 1 0 0 0 установка 1 запрещен
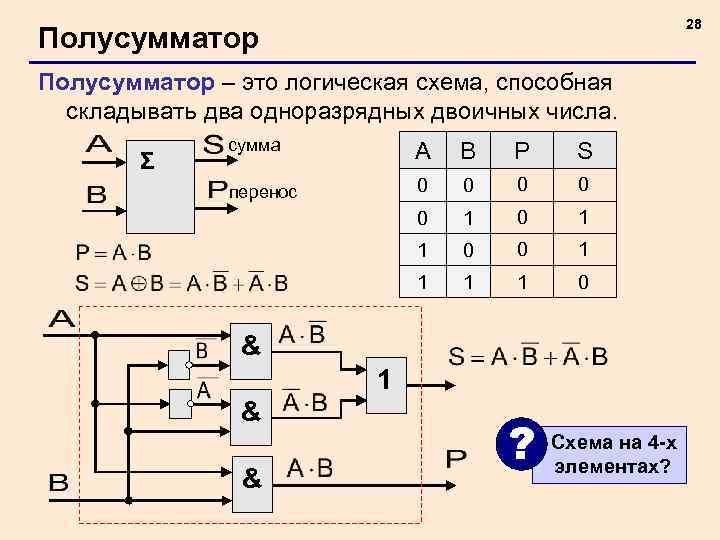
28 Полусумматор – это логическая схема, способная складывать два одноразрядных двоичных числа. Σ сумма A B P S перенос 0 0 0 1 1 0 & 1 & & ? Схема на 4 -х элементах?

29 Логические задачи

30 Метод рассуждений Задача 1. Министры иностранных дел России, США и Китая обсудили за закрытыми дверями проекты договора, представленные каждой из стран. Отвечая затем на вопрос журналистов: "Чей именно проект был принят? ", министры дали такие ответы: Россия — "Проект не наш (1), проект не США (2)"; США — "Проект не России (1), проект Китая (2)"; Китай — "Проект не наш (1), проект России (2)". Один из них оба раза говорил правду; второй – оба раза говорил неправду, третий один раз сказал правду, а другой раз — неправду. Кто что сказал? проект США (? ) проект Китая (? ) (1) (2) проект России (? ) (1) (2) Россия + – Россия + + Россия – + США + – США + + США – Китай + – + Китай
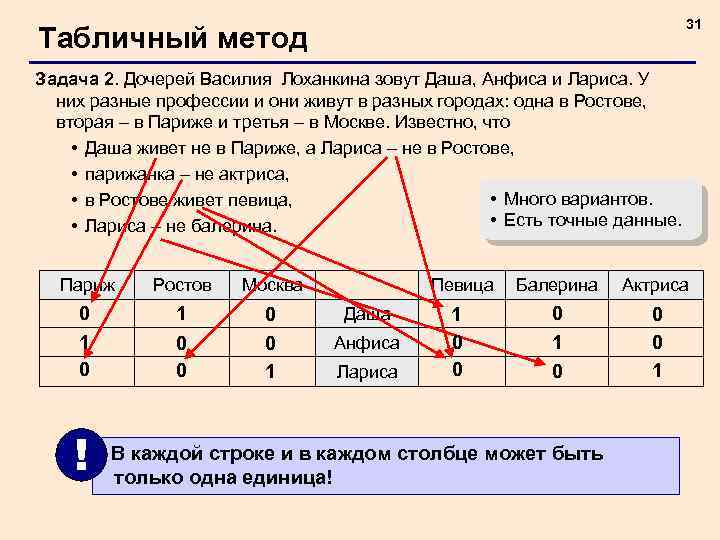
31 Табличный метод Задача 2. Дочерей Василия Лоханкина зовут Даша, Анфиса и Лариса. У них разные профессии и они живут в разных городах: одна в Ростове, вторая – в Париже и третья – в Москве. Известно, что • Даша живет не в Париже, а Лариса – не в Ростове, • парижанка – не актриса, • Много вариантов. • в Ростове живет певица, • Есть точные данные. • Лариса – не балерина. Париж Ростов Москва 0 1 0 0 1 ! Певица Даша Анфиса Лариса 1 0 0 Балерина Актриса 0 1 0 0 0 1 В каждой строке и в каждом столбце может быть только одна единица!

Задача Эйнштейна 32 Условие: Есть 5 домов разного цвета, стоящие в ряд. В каждом доме живет по одному человеку отличной от другого национальности. Каждый жилец пьет только один определенный напиток, курит определенную марку сигарет и держит животное. Никто из пяти человек не пьет одинаковые напитки, не курит одинаковые сигареты и не держит одинаковых животных. Известно, что: 1. Англичанин живет в красном доме. 2. Швед держит собаку. 3. Датчанин пьет чай. 4. Зеленой дом стоит слева от белого. 5. Жилец зеленого дома пьет кофе. 6. Человек, который курит Pallmall, держит птицу. 7. Жилец среднего дома пьет молоко. 8. Жилец из желтого дома курит Dunhill. 9. Норвежец живет в первом доме. 10. Курильщик Marlboro живет около того, кто держит кошку. 11. Человек, который содержит лошадь, живет около того, кто курит Dunhill. 12. Курильщик Winfield пьет пиво. 13. Норвежец живет около голубого дома. 14. Немец курит Rothmans. 15. Курильщик Marlboro живет по соседству с человеком, который пьет воду. Вопрос: У кого живет рыба?
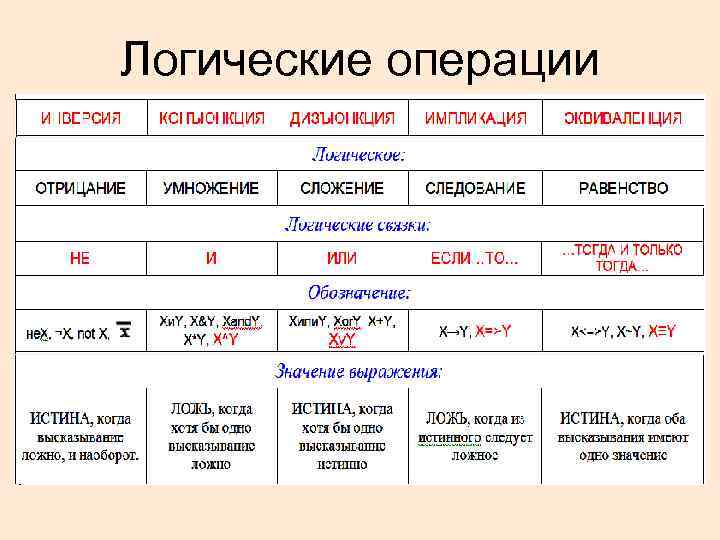
Логические операции
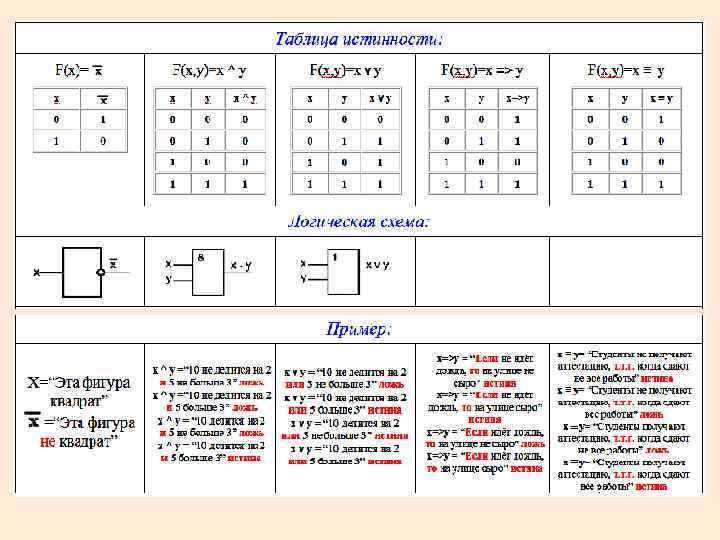
logic.ppt